2.5. Game Theory
The design theory we discussed so far exclusively focused on a situation in which a single decision maker needs to find a best possible decision among alternatives. A decision needed to be made by one decision maker to produce maximum payoffs in single or multiple attributes (or criteria) under a set of constraints. In many situations, however, the payoff of a decision made by an individual depends not only on what he or she does but also on the outcome of the decisions or choices that other individuals make. In engineering design, design decisions are often not made by a single designer or a single design team. Instead, multiple designers or multiple design teams are working on the product design and are involved in design decision making, with each designer or team being responsible for one of more design objectives and/or subsystems. For example, a structural engineer focuses on maximizing the strength and durability of a load-bearing component, while the goal of a manufacturing engineer is to produce the component with least cost in less time. Design decisions made by the structural engineer in determining the geometric shape of the component may affect the cost and time of manufacturing the component and vice versa.
In practice, some of the design decisions are made simultaneously at a specific time of a design phase, and some are made in sequence throughout the design process. With several designers (or design teams) each with his or her own objectives, the nature of the design decisions can take several paths and the overall design may not be desired. This is because that a single designer or team can theoretically do better and his or her decision could dominate, hence largely determining the performance of the overall product, which may or may not be desired.
Game theory applied to this situation provides a method for understanding and perhaps guiding the design decision making. Game theory is a study of strategic decision making. More formally, it is the study of mathematical models of conflict and cooperation between intelligent, rational decision makers. As such, game theory could serve as an important and effective management tool for use in the situations of multiple designers or multiple design teams that are decentralized.
Game theory is mainly used in economics, political science, and psychology, as well as logic and biology. It was recently explored for engineering design. Our purpose of discussing game theory and later employing the theory as a design tool in Section 2.6.2 is not to offer a complete solution for design decision making but to present a plausible idea that has been explored for its feasibility for support of engineering design. As of now, applying game theory as a design tool is still an open research topic that requires much effort to convert the theory into practical tools in the near future.
In the following, we first discuss in Section 2.5.1 the elements of a game and the strategy to determine an equilibrium (or a rational solution) to the game; that is, a stable state in which either one outcome occurs or a set of outcomes occur with known probability. Then, in Section 2.5.2, we present a two-person matrix game and discuss Nash equilibrium for the game. The information presented in these two subsections should provide enough information for readers to proceed with two other kinds of games, sequential games and cooperative games, which are discussed in Sections 2.5.4 and 2.5.5, respectively. To minimize the complexity in mathematical discussion, we assume for most cases two-player games. Readers are referred to the literature (e.g., Aliprantis and Chakrabarti 2006; Hazelrigg 1996) for a more thorough and in-depth discussion of the subject.
2.5.1. Elements of a Game
We start by introducing a well-known game in the literature: the prisoner's dilemma game or prisoner's game. Thereafter, we introduce basic elements in a game by referring to the prisoner's game as an example. With this basic understanding, we proceed with formulating a game mathematically.
In the prisoner's game, two criminals are apprehended by the police, who have strong evidence that they are guilty of the crime, but only weak evidence that they are guilty of a second. Without a confession by one criminal or the other, a conviction for the second crime cannot be obtained. Upon capture, the criminals are immediately separated for interrogation. They are both told that existing evidence will convict them of the first crime, and for that they will each serve 5 years in jail. However, they are offered the opportunity to confess to the second crime. If one confesses and the other one does not, the confessor will have his sentence reduced to 3 years, while the other will have his sentence lengthened to 10 years. But if both confess, both their sentences will be lengthened to 8 years. Certainly, the criminals desire to serve less time in jail. Therefore, a payoff table with negative of the time served in jail is constructed in Table 2.10. The first numeric figure in the pair denotes the payoff for prisoner A and the second for prisoner B.
If the prisoners could hold each other to binding agreements, both would be better off if neither confessed; in this case, each gets 5 years. This is a so-called cooperative game because both players cooperate to maximize their collective payoffs. Acting alone, the better strategy for each is to confess. This is a so-called noncooperative game. If prisoner A chooses to confess, B gets 10 years if he withholds or 8 years if he confesses. If A chooses to withhold, B gets 5 years if he withholds and only 3 years if he confesses. In short, no matter what A does, B is better off by confessing. We say that the strategy of confessing is a strictly dominant strategy for B. The same applies to A. Thus, both prisoners confess, and both are worse off for their actions.
In the absence of any communication or any coordination scheme, rational players are expected to play their strictly dominant strategies because a strictly dominant strategy gives a player an unequivocally higher payoff. A solution to the prisoner's dilemma game can therefore end up being (confess, confess). This is the solution using strictly dominant strategies. The solution (confess, confess) is called the Nash equilibrium, which will be discussed further shortly.
In this prisoner's game—and any game in general—the following elements are present:
1. There are two (or more) participants (or players). In this example, there are two criminals, A and B.
2. Each player has a set of alternative choices, and a player can take action on the available choices. In this example, each criminal can choose to confess or withhold. We denote by ai a choice that player i can make. We refer to the set of choices available to the player i as player i's action set, Ai = {ai}.
3. Each player develops a strategy to play the game. A strategy si is a rule to tell player i which available actions to choose, subject to available information, each time he or she takes an action. In this example, the strategy set for criminal B that maximizes payoffs (provided that information of A's action is available) includes: if A confesses, B confesses; if A withholds, B confesses. The strategies available to player i are referred to as the player's strategy set or strategy space Si = {si}. For all n players in a game, we define the strategy combination or strategy profile s = (s1, s2, …, sn). For the prisoner's game, the strategy combination is s = (sA, sB).
4. For each outcome, there is a payoff that each player gets. In the case of the prisoner's game, the payoffs are given by the pairs (a, b) for each outcome, as shown in Table 2.10.
The above are the essential ingredients that constitute what is called a game in strategic form (or normal form). Note that, as seen in (2) and (3), we use action and strategy interchangeably. In general, a strategic form game consists of a set of players; for each player, there is a strategy set; and for each outcome (or strategy combination) of the game, there is a payoff for each player. When a game is presented in normal form, it is presumed that each player acts simultaneously or, at least, without knowing the actions of the other. If players have some information about the choices of other players, the game is usually presented in extensive form (or tree form). We discuss the extensive form of a sequential game in Section 2.5.3.
Next, we formulate the game mathematically and discuss solution techniques. We focus on two-player games in a matrix form first.
2.5.2. Two-Person Matrix Games
A matrix game, such as the prisoner's dilemma game, is a two-player game such that:
1. Player A has a finite strategy set SA with m elements; that is, SA = {sA1, sA2, …, sAm}. In the prisoner's dilemma game, SA = {sA1 = confess, sA2 = withhold}.
2. Player B has a finite strategy set SB with n elements; that is, SB = {sB1, sB2, …, sBn}. In the prisoner's dilemma game, SB = {sB1 = confess, sB2 = withhold}.
3. Denoting sA an element of set SA (i.e., sA ∈ SA) and sB an element of set SB (i.e., sB ∈ SB), the payoffs of the players are measured by utility functions uA(sA,sB) ∈ R and uB(sA,sB) ∈ R (R is a real number) of the outcomes, in which s = (sA,sB) ∈ SA × SB. For example, in the prisoner's game, uA(sA1 = confess, sB2 = withhold) = −3, and uB(sA1 = confess, sB2 = withhold) = −10. s = (sA,sB) is called a strategy combination or a strategy profile.
Mathematically, the matrix game formulated above can be described as follows: At a certain time, player A chooses a strategy sA ∈ SA. Simultaneously and independently, player B chooses a strategy sB ∈ SB. Once this is done or once a strategy profile s = (sA,sB) is determined, each player receives the respective payoff aij = uA(sAi,sBj) and bij = uB(sAi,sBj). The payoffs can be arranged in the form of an m × n matrix shown in Table 2.11.
The idea of a solution of a game is usually identified by the concept of the Nash equilibrium, defined next.
A pair of strategies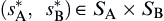 
is a Nash equilibrium of a matrix game if
is a Nash equilibrium of a matrix game if
(2.19)
(2.20)
in which the strictly dominant strategies are followed. In fact, a Nash equilibrium is an outcome of the game from which none of the players have an incentive to deviate. This is because it is optimal for a player to choose the Nash equilibrium strategy. In this sense, a Nash equilibrium has a property that is self-enforcing. Example 2.4 provides more illustration.
Finding the Nash equilibrium by verifying Eqs 2.19 and 2.20 for all possible strategies may not be practical, especially when there are more than two players and each player is given a large strategy set. There are numerous ways to find the Nash equilibrium. In this subsection, we present the approach of a necessary condition learned in Calculus followed by Example 2.5 for illustration. Later, in Section 2.6.2, we employ a graphical approach for a pressure vessel design problem.
We assume the strategy sets are open intervals of real numbers and the payoff functions are differentiable. In this case, a necessary condition for a strategy set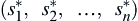 
of an n-player game to be a Nash equilibrium of the game is
of an n-player game to be a Nash equilibrium of the game is
(2.21)
When the system of equations of Eq. 2.21 has a unique solution, then it is the only possible Nash equilibrium of the game. In many cases, the Nash equilibrium is not unique. In some situation, other factors need to be considered to verify that the solution is the Nash equilibrium of the game—for example, second derivatives of the payoff functions with respect to the strategy set.
EXAMPLE 2.4
Verify that in the prisoner's dilemma example, the pair of strategies (confess, confess) is a Nash equilibrium and (withhold, withhold) is not.
Solutions
In the prisoner's dilemma example, the strategy sets for players A and B are, respectively, SA = {sA1 = confess, sA2 = withhold} and SB = {sB1 = confess, sB2 = withhold}, and m = n = 2. The pair of strategies 
is a Nash equilibrium because, for player A,
is a Nash equilibrium because, for player A,1. 
for each sA ∈ SA; that is, 
and 
.
for each sA ∈ SA; that is, and .For player B,
2. 
for each sB ∈ SB; that is, 
and 
and 
.
for each sB ∈ SB; that is, and and .Note that if both players withhold, each receives a 5-year sentence, which seems to be a better solution to the situation. Is it a Nash equilibrium? Let us take a look. For player A,
1. 
, and 
and 
. Therefore, 
does not hold.
, and and . Therefore, does not hold.For player B,
2. 
, and 
and 
. Therefore, 
does not hold.
, and and . Therefore, does not hold.The next example is extracted from Aliprantis and Chakrabarti (2006) and is called the Cournot duopoly model, initially analyzed by French mathematician Augustin Cournot (Example 2.5).
2.5.3. Sequential Games
A sequential game involves multiple players who do not make decisions simultaneously, and one player's decision affects the outcomes and decisions of other players. A sequential game is represented by a game tree (also called the extensive form) with players moving sequentially. We assume information is perfectly known to a player at the time of decision making.
Consider a simple two-person sequential game of two stages with perfect information, whose game tree is shown in Figure 2.13. Here, each vertex (or node) represents a point of choice for a player. The player is specified by an alphabet listed by the vertex. The arrow out of the vertex represents a possible action for that player. The payoffs are specified at the terminal nodes placed at bottom of the tree. Two-stage implies that decisions are made in two stages, one by each player.
In the game shown in Figure 2.13, there are two players. Player A moves first and chooses either L1 or R1. Player B sees player A's move and then chooses L2 or R2, or L3 or R3 depending on player A's move. Suppose that player A chooses L1; then, node 2 is reached; if player B chooses L2, in which terminal node 4 is reached, then player A gets 2 and player B gets 1. If player A chooses R1, then node 3 is reached and if player B chooses R3, then node 7 is reached; then, player A gets 1 and player B gets 0. Now, we are ready to define a sequential game of two players.
A tree T is said to be a two-player game tree if the following are true:
1. Each nonterminal node of the tree is owned by exactly one player. For example, in Figure 2.13, node 1 is owned by player A, and nodes 2 and 3 are owned by player B.
EXAMPLE 2.5
Two firms, firm 1 and firm 2, produce an identical product of amount q1 and q2, respectively. The price per unit of the product in the market is determined by p(q) = A – q, where q = q1 + q2, and A is a fixed number. The price equation shows that the per-unit price of the product is decreasing with an increasing total production amount q = q1 + q2. Assume that the total cost for firm i of producing the output qi is Ci = ciqi, where ci is cost per unit, a positive number. What are the optimal outputs q1 and q2 that each firm should produce in order to maximize profit? Note that the profit of each firm depends on the output of the other firm. They choose their production quantities independently and simultaneously. There is no communication or binding agreement between the firms in regard to the production quantities.
Solutions
This problem can be modeled as a two-player matrix game that is noncooperative. It is reasonable to think of the Nash equilibrium as a self-enforced solution. We find the Nash equilibrium of the game using the first-order derivative test of Eq. 2.21.
We first formulate an equation describing profit as function of quantities. For firms 1 and 2, we have, respectively,
(2.22)
and
(2.23)
(2.24)
(2.25)
(2.26)
(2.27)
Note that if A > c1 + c2, then 
and 
, implying that both firms produce a positive output at the Nash equilibrium.
and , implying that both firms produce a positive output at the Nash equilibrium.
2. At each terminal node v of the tree, a payoff vector is assigned; that is, u(v) = (uA(v), uB(v)). For example, at terminal node 4, u(4) = (2,1), as shown in Figure 2.13.
The above definition for a sequential game of two players can be easily extended to that of n players.
A strategy for a player i in a sequential game consists of the choices that the player is going to make at the nodes he or she owns. As illustrated in Figure 2.13, a strategy for a player in a sequential game is a complete plan of how to play the game, prescribing the choices at every node owned by the player. For example, in Figure 2.13, at node 2, two choices are available for player B: L2 and R2. In other words, a player's strategy will indicate the choices that the player has planned to make a priori (i.e., before the game starts). A strategy profile for a two-person sequential game is then represented as s = (sA, sB), where each sA and sB is a strategy for players A and B, respectively. For example, as shown in Figure 2.13, SA can be L1 or R1, and SB is a function from {node 2, node 3} to {sB21 = L2, sB22 = R2; sB31 = L3, sB32 = R3} with the feasibility restriction that, from node 2, player B can only choose L2 or R2 with a similar restriction on choices from node 3. In other words, the choice of player B depends on the choice made by player A according to the prescribed game tree. Note that a strategy profile uniquely determines the terminal node v that is reached. The payoff (or utility) of each player is a function uA and uB of the strategy profile (sA, sB).
A solution of a sequential game is also understood to be a Nash equilibrium. In a two-player sequential game, a strategy profile 
is said to be a Nash equilibrium if, for each player, we have
is said to be a Nash equilibrium if, for each player, we have
(2.28)
(2.29)
In other words, a Nash equilibrium is a strategy profile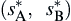 
such that player A cannot improve his payoff by changing his strategy if the player B does not change, and vice versa. Note that Eqs 2.28 and 2.29 are identical to those of Eqs 2.19 and 2.20 in a strategy form game.
such that player A cannot improve his payoff by changing his strategy if the player B does not change, and vice versa. Note that Eqs 2.28 and 2.29 are identical to those of Eqs 2.19 and 2.20 in a strategy form game.A backward induction method is often employed to solve for the Nash equilibrium of a sequential game. Backward induction is the process of reasoning backward in time, from the end of a problem or situation, to determine a sequence of optimal actions. It proceeds by first considering the last time a decision might be made and choosing what to do in any situation at that time. Using this information, one can then determine what to do at the second-to-last time of decision. This process continues backward until one has determined the best action for every possible situation at every point in time. We illustrate the use of the method in the following example (Example 2.6).
EXAMPLE 2.6
Find the Nash equilibrium for the sequential game shown in Figure 2.13.
Solutions
We use the backward induction and conditions shown in Eqs 2.28 and 2.29 to find the Nash equilibrium.
We first assume 
, then 
because uB(L1, R2) = 3 ≥ {uB(L1, R2) = 3, uB(L1, L2) = 1}. If 
, then 
because uB(R1, L3) = 1 ≥ {uB(R1, L3) = 1, uB(R1, R3) = 0}.
, then because uB(L1, R2) = 3 ≥ {uB(L1, R2) = 3, uB(L1, L2) = 1}. If , then because uB(R1, L3) = 1 ≥ {uB(R1, L3) = 1, uB(R1, R3) = 0}.Now, we go backward and use Eq. 2.28 to find 
from the two strategies (L1, R2) and (R1, L3). We found that 
because uA(R1, L3) = 4 ≥ {uA(R1, L3) = 4, uA(L1, R2) = 3}. Hence the Nash equilibrium is found at 
—that is, the path 1 → 3 → 6. If player B does not change its strategy 
, player A cannot improve its payoff by changing its strategy—for example, from R1 to L1. Similarly, if player A does not change its strategy 
, player B cannot improve its payoff by changing its strategy—for example, from L3 to R3.
from the two strategies (L1, R2) and (R1, L3). We found that because uA(R1, L3) = 4 ≥ {uA(R1, L3) = 4, uA(L1, R2) = 3}. Hence the Nash equilibrium is found at —that is, the path 1 → 3 → 6. If player B does not change its strategy , player A cannot improve its payoff by changing its strategy—for example, from R1 to L1. Similarly, if player A does not change its strategy , player B cannot improve its payoff by changing its strategy—for example, from L3 to R3.The next example (Example 2.7) is again extracted from Aliprantis and Chakrabarti (2006), called the Stackelberg duopoly model, which is slightly modified from the example of the Cournot duopoly model to illustrate a few more details of the sequential game.
EXAMPLE 2.7
Continue with Example 2.5, except that firm 1 chooses a production quantity q1 ≥ 0. Firm 2 observes q1 and then chooses its own production quantity q2. Find the optimal production quantities q1 and q2 each firm should produce in order to maximize profit.
Solutions
This problem can be formulated as a two-person sequential game of two stages and with perfect information. We use backward induction again for this problem. We first find the output 
of firm 2 that maximizes firm 2's profit given the output q1 of firm 1. That is, 
. The profit of firm 2 can be formulated as
of firm 2 that maximizes firm 2's profit given the output q1 of firm 1. That is, . The profit of firm 2 can be formulated as
(2.30)
Taking the first and second derivatives of Eq. 2.30 with respect to q2, we have
(2.31)
and
(2.32)
Solving for q2 from Eq. 2.31, we have
(2.33)
which gives maximum profit u2 for firm 2, provided q1 < A − c2 (so that 
).
).Firm 1 should now anticipate that firm 2 will choose 
if firm 1 chooses q1. Therefore, firm 1 will want to choose q1 to maximize its profit, defined as
if firm 1 chooses q1. Therefore, firm 1 will want to choose q1 to maximize its profit, defined as
(2.34)
subject to q1 ≥ 0. Taking again the first and second derivatives of Eq. 2.34 with respect to q1, we have
(2.35)
and
(2.36)
Therefore, from Eq. 2.35, we have
(2.37)
(2.38)
2.5.4. Cooperative Games
Now we go back to the prisoner's game. We have observed that both criminals in the prisoner's game are better off if they both withhold. This is the basis for one solution concept in cooperative games.
First, we define a criterion to rank outcomes from the point of view of the group of players as a whole. We can say that one outcome is better than another if at least one player is better off and no one is worse off. For example, in the prisoner's game, (withhold, withhold) is better than (confess, confess). This is called the Pareto criterion, after the Italian economist and mechanical engineer, Vilfredo Pareto. If an outcome cannot be improved, then we say that the outcome is Pareto optimal—that is, optimal in terms of the Pareto criterion. In the prisoner's game, (withhold, withhold) is Pareto optimal because no one can be made better off without making the other prisoner worse off. In fact, (confess, withhold) is also Pareto optimal because neither player is better off without making the other player worse off.
Mathematically, the Pareto solution for a two-person game can be defined as follows:
(2.39)
It is obvious that s∗ = (withhold, withhold) satisfies Eq. 2.39.
If there were a unique Pareto optimal outcome for a cooperative game, that would seem to be a good solution concept. However, there is not. For example, in the prisoner's game, u(confess, withhold) = (−3, −10) is also a Pareto solution (see Example 2.8). In general, there are infinitely many Pareto optima for any fairly complicated game. Pareto optimal and solution techniques will be formally introduced in Chapter 5 under the subject of multiobjective optimization. In general, Pareto optimal or Pareto solutions are better understood in the so-called criterion space. We use the Cournot duopoly model to illustrate Pareto optimal in Example 2.9.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.