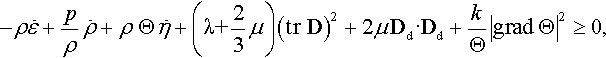Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Appendix E

Energy Formulations and Stability Conditions for Newtonian Fluids

In this section, we review and augment the thermomechanical theory for compressible Newtonian fluids presented in Chapter 7 and discuss the corresponding stability conditions.

E.1 Governing equations

Recall that the fundamental laws for a continuum in the thermomechanical theory are

$\dot{ρ} + ρ div v = 0, ρ \dot{v} = div T + ρ b, ρ \dot{ε} = T \cdot D + ρ r - div q,$ $\dot{ρ} + ρ div v = 0, ρ \dot{v} = div T + ρ b, ρ \dot{ε} = T \cdot D + ρ r - div q,$

(E.1)

which correspond to Eulerian statements of conservation of mass, linear momentum, and energy; refer to Section 5.3. In (E.1), ρ is the density, v is the velocity, T is the Cauchy stress, b is the body force per unit mass, ε is the internal energy per unit mass, r is the rate of heat absorbed per unit mass, q is the heat flux vector, and

$D = \frac{1}{2} [grad v + {(grad v)}^{T}]$ $D = \frac{1}{2} [grad v + {(grad v)}^{T}]$

si2_e

is the rate of deformation. A compressible Newtonian fluid (refer to Section 7.2.1.2) is characterized by the constitutive equations

$T = - p I + λ (tr D) I + 2 μ D, q = - k grad Θ,$ $T = - p I + λ (tr D) I + 2 μ D, q = - k grad Θ,$

(E.2)

where p is the pressure, Θ is the absolute temperature, λ and μ are the dilatational and shear viscosities, respectively, and k is the thermal conductivity. The second law of thermodynamics in the form of the Clausius-Duhem inequality is

$- ρ \dot{ε} + T \cdot D + ρ Θ \dot{η} - \frac{1}{Θ} q \cdot grad Θ \geq 0,$ $- ρ \dot{ε} + T \cdot D + ρ Θ \dot{η} - \frac{1}{Θ} q \cdot grad Θ \geq 0,$

si4_e (E.3)

where η is the entropy per unit mass. It can be verified that use of the constitutive equations (E.2) in the second law (E.3), and subsequent decomposition of the rate of deformation D into its spherical (volumetric) and deviatoric (traceless) parts, i.e.,

$D = \frac{1}{3} (tr D) I + D_{d},$ $D = \frac{1}{3} (tr D) I + D_{d},$

si5_e

leads to

$- ρ \dot{ε} + \frac{p}{ρ} \dot{ρ} + ρ Θ \dot{η} + (λ+ \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0,$ $- ρ \dot{ε} + \frac{p}{ρ} \dot{ρ} + ρ Θ \dot{η} + (λ+ \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0,$

si6_e (E.4)

where we have used

$\dot{ρ} = - ρ div v = - ρ tr D = - ρ I \cdot D .$ $\dot{ρ} = - ρ div v = - ρ tr D = - ρ I \cdot D .$

The mathematical model for a compressible Newtonian fluid is completed by specifying the equations of state. In the following sections, we present four equivalent formulations of the equations of state, each employing a different set of independent variables: density ρ or pressure p for the independent mechanical variable, and entropy η or temperature Θ for the independent thermal variable. (Recall that only the density-temperature formulation—with ρ as the independent mechanical variable and Θ as the independent thermal variable—was explored in Section 7.2.1.2.)

E.1.1 Density-entropy formulation

The system formulation (E.1) and (E.2) implicitly uses three choices: density ρ as the independent mechanical variable, entropy η as the independent thermal variable, and internal energy $\overset{˘}{ε} (ρ, η)$ $\overset{˘}{ε} (ρ, η)$ as the thermodynamic energy potential. Use of the chain rule

$\dot{ε} = \frac{\partial \overset{˘}{ε}}{\partial ρ} \dot{ρ} + \frac{\partial \overset{˘}{ε}}{\partial η} \dot{η}$ $\dot{ε} = \frac{\partial \overset{˘}{ε}}{\partial ρ} \dot{ρ} + \frac{\partial \overset{˘}{ε}}{\partial η} \dot{η}$

si9_e

in the second law (E.4) gives

$\frac{1}{ρ} (p - ρ^{2} \frac{\partial \overset{˘}{ε}}{\partial ρ}) \dot{ρ} + ρ (Θ - \frac{\partial \overset{˘}{ε}}{\partial η}) \dot{η} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$ $\frac{1}{ρ} (p - ρ^{2} \frac{\partial \overset{˘}{ε}}{\partial ρ}) \dot{ρ} + ρ (Θ - \frac{\partial \overset{˘}{ε}}{\partial η}) \dot{η} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$

si10_e (E.5)

Using arguments similar to those employed in Section 7.2.1.2, we can prove that as a consequence of inequality (E.5),

$p = ρ^{2} \frac{\partial \overset{˘}{ε}}{\partial ρ}, Θ = \frac{\partial \overset{˘}{ε}}{\partial η}$ $p = ρ^{2} \frac{\partial \overset{˘}{ε}}{\partial ρ}, Θ = \frac{\partial \overset{˘}{ε}}{\partial η}$

si11_e (E.6a)

and

$λ + \frac{2}{3} μ \geq 0, μ \geq 0, k \geq 0 .$ $λ + \frac{2}{3} μ \geq 0, μ \geq 0, k \geq 0 .$

si12_e (E.6b)

With the internal energy $\overset{˘}{ε} (ρ, η)$ $\overset{˘}{ε} (ρ, η)$ a specified function of ρ and η, the equations of state (E.6a)₁ and (E.6a)₂ prescribe the dependent mechanical and thermal variables p and Θ in terms of the independent mechanical and thermal variables ρ and η. Equation (E.6b) demands nonnegativity of the bulk viscosity, shear viscosity, and thermal conductivity. Note that the material parameters λ, μ, and k may depend on the density ρ and entropy η. The conservation laws (E.1), constitutive equations (E.2), and equations of state (E.6a) constitute a closed system for the primitive quantities ρ, η, and v.

E.1.2 Density-temperature formulation

In this formulation, density ρ is the independent mechanical variable, temperature Θ is the independent thermal variable, and the Helmholtz free energy $\overset{˘}{ψ} (ρ, Θ)$ $\overset{˘}{ψ} (ρ, Θ)$ is the thermodynamic energy potential. The Helmholtz free energy $\overset{˘}{ψ} (ρ, Θ)$ $\overset{˘}{ψ} (ρ, Θ)$ is defined by the Legendre transformation of internal energy $\overset{˘}{ε} (ρ, η)$ $\overset{˘}{ε} (ρ, η)$ with respect to the thermal variable, from η to Θ,

$ψ = ε - Θ η .$ $ψ = ε - Θ η .$

(E.7)

See also (5.33). Taking the material derivative of (E.7), we obtain

$\dot{ψ} = \dot{ε} - Θ \dot{η} - η \dot{Θ},$ $\dot{ψ} = \dot{ε} - Θ \dot{η} - η \dot{Θ},$

si18_e

so inequality (E.4) becomes

$- ρ \dot{ψ} + \frac{p}{ρ} \dot{ρ} - ρ η \dot{Θ} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$ $- ρ \dot{ψ} + \frac{p}{ρ} \dot{ρ} - ρ η \dot{Θ} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$

si19_e (E.8)

Use of the chain rule

$\dot{ψ} = \frac{\partial \overset{˘}{ψ}}{\partial ρ} \dot{ρ} + \frac{\partial \overset{˘}{ψ}}{\partial Θ} \dot{Θ}$ $\dot{ψ} = \frac{\partial \overset{˘}{ψ}}{\partial ρ} \dot{ρ} + \frac{\partial \overset{˘}{ψ}}{\partial Θ} \dot{Θ}$

si20_e

in the second law inequality (E.8) leads to

$\frac{1}{ρ} (p - ρ^{2} \frac{\partial \overset{˘}{ψ}}{\partial ρ}) \dot{ρ} - ρ (η + \frac{\partial \overset{˘}{ψ}}{\partial Θ}) \dot{Θ} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$ $\frac{1}{ρ} (p - ρ^{2} \frac{\partial \overset{˘}{ψ}}{\partial ρ}) \dot{ρ} - ρ (η + \frac{\partial \overset{˘}{ψ}}{\partial Θ}) \dot{Θ} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$

si21_e

Using standard arguments, we obtain

$p = ρ^{2} \frac{\partial \overset{˘}{ψ}}{\partial ρ}, η = - \frac{\partial \overset{˘}{ψ}}{\partial Θ}$ $p = ρ^{2} \frac{\partial \overset{˘}{ψ}}{\partial ρ}, η = - \frac{\partial \overset{˘}{ψ}}{\partial Θ}$

si22_e (E.9a)

and

$λ + \frac{2}{3} μ \geq 0, μ \geq 0, k \geq 0 .$ $λ + \frac{2}{3} μ \geq 0, μ \geq 0, k \geq 0 .$

si23_e (E.9b)

See also (7.32). Note that the material parameters λ, μ, and k may depend on the density ρ and temperature Θ. With the Helmholtz free energy $\overset{˘}{ψ} (ρ, Θ)$ $\overset{˘}{ψ} (ρ, Θ)$ a specified function of ρ and Θ, (E.1), (E.2), (E.7), and (E.9a) form a closed system for ρ, Θ, and v.

E.1.3 Pressure-entropy formulation

In this formulation, pressure p is the independent mechanical variable, entropy η is the independent thermal variable, and enthalpy $\overset{˘}{χ} (p, η)$ $\overset{˘}{χ} (p, η)$ is the thermodynamic energy potential. The enthalpy $\overset{˘}{χ} (p, η)$ $\overset{˘}{χ} (p, η)$ is defined by the Legendre transformation of internal energy $\overset{˘}{ε} (ρ, η)$ $\overset{˘}{ε} (ρ, η)$ with respect to the mechanical variable, from specific volume 1/ρ to pressure p,

$χ = ε + \frac{1}{ρ} p .$ $χ = ε + \frac{1}{ρ} p .$

(E.10)

The rate of the Legendre transformation (E.10) is

$\dot{χ} = \dot{ε} + \frac{1}{ρ} \dot{p} - \frac{p}{ρ^{2}} \dot{ρ} .$ $\dot{χ} = \dot{ε} + \frac{1}{ρ} \dot{p} - \frac{p}{ρ^{2}} \dot{ρ} .$

si29_e (E.11)

Substitution of (E.11) into the second law inequality (E.4) gives

$- ρ \dot{χ} + \dot{ρ} - ρ Θ \dot{η} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$ $- ρ \dot{χ} + \dot{ρ} - ρ Θ \dot{η} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$

si30_e

Subsequent use of the chain rule on $\dot{χ}$ $\dot{χ}$ leads to

$(1 - ρ \frac{\partial \overset{˘}{χ}}{\partial p}) \dot{p} - ρ (Θ + \frac{\partial \overset{˘}{χ}}{\partial η}) \dot{η} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0,$ $(1 - ρ \frac{\partial \overset{˘}{χ}}{\partial p}) \dot{p} - ρ (Θ + \frac{\partial \overset{˘}{χ}}{\partial η}) \dot{η} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0,$

si32_e

from which it follows that

$\frac{1}{ρ} = \frac{\partial \overset{˘}{χ}}{\partial p}, Θ = \frac{\partial \overset{˘}{χ}}{\partial η}$ $\frac{1}{ρ} = \frac{\partial \overset{˘}{χ}}{\partial p}, Θ = \frac{\partial \overset{˘}{χ}}{\partial η}$

si33_e (E.12a)

and

$λ + \frac{2}{3} μ \geq 0, μ \geq 0, k \geq 0 .$ $λ + \frac{2}{3} μ \geq 0, μ \geq 0, k \geq 0 .$

si34_e (E.12b)

Note that the material parameters λ, μ, and k may depend on the pressure p and entropy η. With the enthalpy $\overset{˘}{χ} (p, η)$ $\overset{˘}{χ} (p, η)$ a specified function of p and η, the equations of state (E.12a) together with the conservation laws (E.1), constitutive equations (E.2), and Legendre transformation (E.10) form a closed system for p, η, and v.

E.1.4 Pressure-temperature formulation

In this formulation, pressure p is the independent mechanical variable, temperature Θ is the independent thermal variable, and the Gibbs free energy $\overset{˘}{φ} (p, Θ)$ $\overset{˘}{φ} (p, Θ)$ is the thermodynamic energy potential. The Gibbs free energy $\overset{˘}{φ} (p, Θ)$ $\overset{˘}{φ} (p, Θ)$ is defined by the Legendre transformation of internal energy $\overset{˘}{ε} (ρ, η)$ $\overset{˘}{ε} (ρ, η)$ with respect to the mechanical and thermal variables, from specific volume 1/ρ to pressure p and entropy η to temperature Θ,

$φ = ε + \frac{1}{ρ} p - Θ η .$ $φ = ε + \frac{1}{ρ} p - Θ η .$

(E.13)

The material derivative of (E.13) is

$\dot{φ} = \dot{ε} + \frac{1}{ρ} \dot{p} - \frac{p}{ρ^{2}} \dot{ρ} - Θ \dot{η} - η \dot{Θ} .$ $\dot{φ} = \dot{ε} + \frac{1}{ρ} \dot{p} - \frac{p}{ρ^{2}} \dot{ρ} - Θ \dot{η} - η \dot{Θ} .$

si40_e (E.14)

Use of (E.14) in the second law (E.4) yields

$- ρ \dot{φ} + \dot{p} - ρ η \dot{Θ} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$ $- ρ \dot{φ} + \dot{p} - ρ η \dot{Θ} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$

si41_e

The chain rule

$\dot{φ} = \frac{\partial \overset{˘}{φ}}{\partial p} \dot{p} + \frac{\partial \overset{˘}{φ}}{\partial Θ} \dot{Θ}$ $\dot{φ} = \frac{\partial \overset{˘}{φ}}{\partial p} \dot{p} + \frac{\partial \overset{˘}{φ}}{\partial Θ} \dot{Θ}$

si42_e

then implies that

$(1 - ρ \frac{\partial \overset{˘}{φ}}{\partial p}) \dot{p} - ρ (η + \frac{\partial \overset{˘}{φ}}{\partial Θ}) \dot{Θ} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$ $(1 - ρ \frac{\partial \overset{˘}{φ}}{\partial p}) \dot{p} - ρ (η + \frac{\partial \overset{˘}{φ}}{\partial Θ}) \dot{Θ} + (λ + \frac{2}{3} μ) {(tr D)}^{2} + 2 μ D_{d} \cdot D_{d} + \frac{k}{Θ} {| grad Θ |}^{2} \geq 0 .$

si43_e

Customary arguments allow us to conclude that

$\frac{1}{ρ} = \frac{\partial \overset{˘}{φ}}{\partial p}, η = - \frac{\partial \overset{˘}{φ}}{\partial Θ}$ $\frac{1}{ρ} = \frac{\partial \overset{˘}{φ}}{\partial p}, η = - \frac{\partial \overset{˘}{φ}}{\partial Θ}$

si44_e (E.15a)

and

$λ + \frac{2}{3} μ \geq 0, μ \geq 0, k \geq 0 .$ $λ + \frac{2}{3} μ \geq 0, μ \geq 0, k \geq 0 .$

si45_e (E.15b)

Note that the material parameters λ, μ, and k may depend on the pressure p and temperature Θ. With the Gibbs free energy $\overset{˘}{φ} (p, Θ)$ $\overset{˘}{φ} (p, Θ)$ a specified function of p and Θ, (E.1), (E.2), (E.13), and (E.15a) constitute a closed system for p, Θ, and v.

E.2 Stability conditions

Stability of the rest state is required for a theory to be physically valid [22, 65]. For a compressible Newtonian fluid, a necessary and sufficient condition for stability of the rest state is that the internal energy ε is a convex function of entropy η and specific volume τ = ρ⁻¹ [66, 67]:

$ε_{τ τ} \geq 0, ε_{η η} \geq 0, ε_{τ τ} ε_{η η} - ε_{τ η}^{2} \geq 0,$ $ε_{τ τ} \geq 0, ε_{η η} \geq 0, ε_{τ τ} ε_{η η} - ε_{τ η}^{2} \geq 0,$

(E.16a)

where subscripts denote partial differentiation, e.g.,

$ε_{τ τ} = \frac{\partial^{2} ε (τ, η)}{\partial τ^{2}} .$ $ε_{τ τ} = \frac{\partial^{2} ε (τ, η)}{\partial τ^{2}} .$

si48_e

With a change of independent variable from specific volume τ to density ρ, condition (E.16a) becomes

$\frac{2 ε_{ρ}}{ρ} + ε_{ρ ρ} \geq 0, ε_{η η} \geq 0, (\frac{2 ε_{ρ}}{ρ} + ε_{ρ ρ}) ε_{η η} - ε_{ρ η}^{2} \geq 0 .$ $\frac{2 ε_{ρ}}{ρ} + ε_{ρ ρ} \geq 0, ε_{η η} \geq 0, (\frac{2 ε_{ρ}}{ρ} + ε_{ρ ρ}) ε_{η η} - ε_{ρ η}^{2} \geq 0 .$

si49_e (E.16b)

Note that one need monitor only two of these inequalities, since (E.16b)₁ and (E.16b)₃ imply (E.16b)₂, and (E.16b)₂ and (E.16b)₃ imply (E.16b)₁. It can be verified that the equivalent conditions on the Helmholtz free energy are

$ψ_{τ τ} \geq 0, ψ_{θ θ} \leq 0, ψ_{τ τ} ψ_{θ θ} - ψ_{τ θ}^{2} \leq 0,$ $ψ_{τ τ} \geq 0, ψ_{θ θ} \leq 0, ψ_{τ τ} ψ_{θ θ} - ψ_{τ θ}^{2} \leq 0,$

(E.17a)

or, upon a change of independent variable from specific volume τ to density ρ,

$\frac{2 ψ_{ρ}}{ρ} + ψ_{ρ ρ} \geq 0, ψ_{θ θ} \leq 0, (ψ_{ρ ρ} + \frac{ψ_{ρ}}{ρ}) ψ_{θ θ} - ψ_{ρ θ}^{2} \leq 0 .$ $\frac{2 ψ_{ρ}}{ρ} + ψ_{ρ ρ} \geq 0, ψ_{θ θ} \leq 0, (ψ_{ρ ρ} + \frac{ψ_{ρ}}{ρ}) ψ_{θ θ} - ψ_{ρ θ}^{2} \leq 0 .$

si51_e (E.17b)

Similarly, we have

$χ_{pp} \leq 0, χ_{η η} \geq 0, χ_{η η} χ_{pp} - χ_{p η}^{2} \leq 0$ $χ_{pp} \leq 0, χ_{η η} \geq 0, χ_{η η} χ_{pp} - χ_{p η}^{2} \leq 0$

(E.18)

for the enthalpy and

$φ_{pp} \leq 0, φ_{θ θ} \leq 0, φ_{pp} φ_{θ θ} - φ_{p θ}^{2} \geq 0$ $φ_{pp} \leq 0, φ_{θ θ} \leq 0, φ_{pp} φ_{θ θ} - φ_{p θ}^{2} \geq 0$

(E.19)

for the Gibbs free energy.

It can be shown (see, for instance, [68]) that for a compressible Newtonian fluid, the convexity conditions (E.16b) on the internal energy are equivalent to (1) nonnegativity of the specific heat at constant volume C_V and the isothermal bulk modulus κ, i.e.,

$C_{V} \equiv Θ \frac{\partial η (τ, Θ)}{\partial Θ} \geq 0, κ \equiv - τ \frac{\partial p (τ, Θ)}{\partial τ} \geq 0,$ $C_{V} \equiv Θ \frac{\partial η (τ, Θ)}{\partial Θ} \geq 0, κ \equiv - τ \frac{\partial p (τ, Θ)}{\partial τ} \geq 0,$

si54_e

and (2) an absence of negative decay rates in the linearized stability analysis of the the rest state. Thus, for a compressible Newtonian fluid, there are three equivalent conditions for stability of the rest state.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Appendix E: Energy Formulations and Stability Conditions for Newtonian Fluids

Create new playlist

Sign In

Sign Up

E.1 Governing equations

E.1.1 Density-entropy formulation

E.1.2 Density-temperature formulation

E.1.3 Pressure-entropy formulation

E.1.4 Pressure-temperature formulation

E.2 Stability conditions

Table of Contents for
Appendix E: Energy Formulations and Stability Conditions for Newtonian Fluids