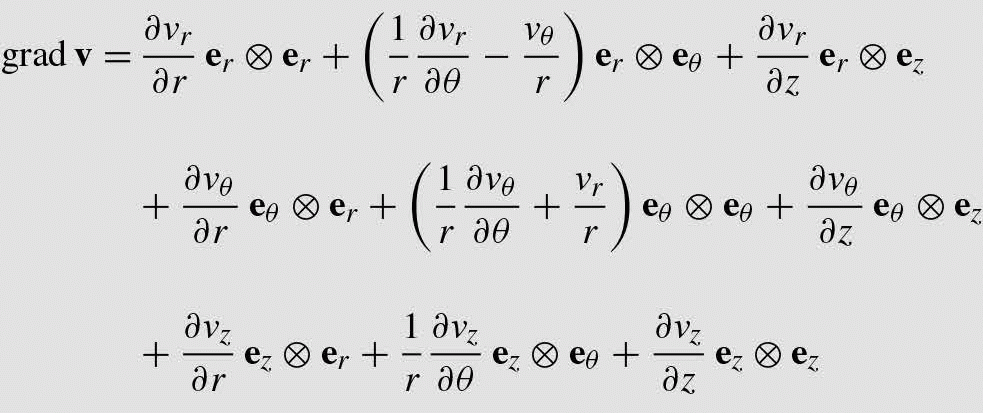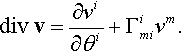2.6 Curvilinear coordinates

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

2.6 Curvilinear coordinates

Recall that any basis for the three-dimensional inner product space $ε^{3}$ has three elements. Also recall that $ε^{3}$ has a fixed orthonormal basis {e_i} = {e₁, e₂, e₃}. As was demonstrated in (2.21), any vector u in $ε^{3}$ can be expressed in terms of this basis, i.e.,

$u = u_{1} e_{1} + u_{2} e_{2} + u_{3} e_{3},$

or, compactly,

$u = u_{i} e_{i} .$

The scalars u₁, u₂, and u₃ are called the Cartesian components of vector u.

Of course, $ε^{3}$ has infinitely many other fixed orthonormal bases, which are merely rotations or inversions of {e₁, e₂, e₃}. It also has infinitely many other bases that are not orthogonal or fixed; components with respect to these bases are called non-Cartesian or curvilinear components. (Because its basis vectors {e₁, e₂, e₃} are fixed and do not change direction or magnitude with position, Cartesian component notation is the simplest to manipulate.)

Since $ε^{3}$ is a metric space (refer to Section 2.1.2 and Figure 2.3), the position vector x in $ε^{3}$ can be considered a point in space, or a vector from the origin to the point. Furthermore,

$x = x_{1} e_{1} + x_{2} e_{2} + x_{3} e_{3},$

or, compactly,

$x = x_{i} e_{i} .$

The Cartesian components x_i of position vector x are called the Cartesian coordinates of the point. The three independent variables x₁, x₂, and x₃ therefore define the position of point x in $ε^{3}$ .

Since e₁, e₂, and e₃ are fixed, the surfaces x_i = constant, called the coordinate surfaces, are planes, and the intersections of two coordinate surfaces, called coordinate curves, are straight lines (see Figure 2.5). For example, the coordinate surface x₁ = C = constant is a plane perpendicular to the unit vector e₁, and the x₁ coordinate line given by x₂ = D = constant, x₃ = ε = constant is a straight line in the e₁ direction.

f02-05-9780123946003 — Figure 2.5 Cartesian coordinate curves, coordinate surfaces, and basis vectors.

When solving boundary-value problems, one adopts coordinate systems (θ¹, θ², θ³) in which the boundary surfaces in the physical problem (where the boundary values are specified) are given by coordinate surfaces θⁱ = constant. Because the coordinate surfaces are planes, Cartesian coordinates are useful for solving boundary-value problems in situations where the boundary surfaces are planes. However, in many problems of interest, the boundary surfaces are not planes, and it is therefore advantageous to adopt curvilinear coordinates.

Since the coordinate surfaces θⁱ = constant in curvilinear coordinate systems are not planar, the coordinate curves (given by the intersection of two coordinate surfaces) are not straight lines. The basis vectors, which are tangent to the coordinate curves, are not fixed, but rather rotate in space with change of position. (Curvilinear coordinates are so called because their coordinate curves are not straight lines.) The most familiar curvilinear coordinates are cylindrical polar coordinates and spherical coordinates.

2.6.1 Covariant and contravariant basis vectors

The natural basis {g_i} = {g₁, g₂, g₃} of the curvilinear coordinate system (θ¹, θ², θ³) is defined by

$g_{i} = \frac{\partial x}{\partial θ^{i}},$

(2.110)

where x is the position vector. The vectors g_i are also called the covariant basis vectors or tangent basis vectors. They are tangent to the coordinate curve: g₁ is tangent to the θ¹ curve at position x, g₂ is tangent to the θ² curve at x, and g₃ is tangent to the θ³ curve at x (see Figure 2.6).

Problem 2.58

Determine the covariant basis {g_i} = {g₁, g₂, g₃} of the cylindrical polar coordinate system (θ¹ = r, θ² = θ, θ³ = z).

Solution

The cylindrical polar coordinate system (r, θ, z) is related to the Cartesian coordinate system (x₁, x₂, x₃) through

$x_{1} = r cos θ, x_{2} = r sin θ, x_{3} = z,$

(a)

so the position vector x is given by

$x = x_{1} e_{1} + x_{2} e_{2} + x_{3} e_{3} = r cos θ e_{1} + r sin θ e_{2} + z e_{3} .$

(b)

Then, from definition (2.110), the covariant basis vectors are

$\begin{array}{l} g_{1} = \frac{\partial x}{\partial r} = cos θ e_{1} + sin θ e_{2}, \\ g_{2} = \frac{\partial x}{\partial θ} = - r sin θ e_{1} + r cos θ e_{2}, \\ g_{3} = \frac{\partial x}{\partial z} = e_{3} . \end{array}$

si488_e (c)

f02-06-9780123946003 — Figure 2.6 Curvilinear coordinate curves and natural (covariant) basis vectors.

In general, the covariant basis vectors g_i are not fixed in either magnitude or direction, and can have dimensions. In the cylindrical polar example (c) of Problem 2.64, the direction of basis vector g₂ at position (r, θ, z) depends on the value of coordinate θ, and its magnitude depends on the value of coordinate r; although g₁ and g₃ are dimensionless unit vectors, g₂ has dimensions of length and is not a unit vector.

The reciprocal basis {gⁱ} = {g¹, g², g³} is defined by

$g^{i} \cdot g_{j} = δ_{j}^{i},$

(2.111)

where δⁱ_j is the Kronecker delta (refer to (2.26)), so g¹ is perpendicular to both g₂ and g₃, and the inner product of g¹ with g₁ is 1, etc. The basis vectors gⁱ are also called the contravariant basis vectors. They are normal to the coordinate surfaces: g¹ is perpendicular to the θ¹ surface at position x, g² is perpendicular to the θ² surface at x, and g³ is perpendicular to the θ³ surface at x (see Figure 2.7).

Problem 2.59

Determine the contravariant basis {gⁱ} = {g¹, g², g³} of the cylindrical polar coordinate system.

Solution

For the cylindrical polar coordinate system, result (c) in Problem 2.64 and definition (2.111) imply that

$\begin{array}{l} g^{1} = cos θ e_{1} + sin θ e_{2} = g_{1}, \\ g^{2} = - \frac{1}{r} sin θ e_{1} + \frac{1}{r} cos θ e_{2} = \frac{1}{r^{2}} g_{2}, \\ g^{3} = e_{3} = g_{3} . \end{array}$

si490_e (a)

f02-07-9780123946003 — Figure 2.7 Curvilinear coordinate surfaces and reciprocal (contravariant) basis vectors.

It can be seen from Figures 2.6 and 2.7 that, in general, the two bases g₁, g₂, g₃ and g¹, g², g³ are along different directions. It is only when the coordinate system is orthogonal, as in the cylindrical polar example, that g_i and gⁱ are along the same directions; even then, however, the magnitudes and dimensions of g_i and gⁱ will differ (compare g₂ in (c) of Problem 2.64 with g² in (a) of Problem 2.65). It is only for a Cartesian coordinate system that the definitions (2.110) and (2.111) produce the same bases:

$g_{i} = g^{i} = e_{i} \Leftrightarrow Cartesian coordinate system .$

Any vector v in $ε^{3}$ can be expressed in terms of either a covariant basis or a contravariant basis, i.e.,

$v = v^{i} g_{i} = v^{1} g_{1} + v^{2} g_{2} + v^{3} g_{3}$

(2.112a)

$v = v_{i} g^{i} = v_{1} g^{1} + v_{2} g^{2} + v_{3} g^{3} .$

(2.112b)

Similarly, any tensor T in $L$ can be be expressed in terms of either a covariant basis or a contravariant basis, i.e.,

$T = T^{ij} g_{i} \otimes g_{j}$

(2.113a)

$T = T_{ij} g^{i} \otimes g^{j} .$

(2.113b)

In curvilinear coordinates it is important to keep track of whether the indices are superscripts or subscripts. The components vⁱ and v_i of vector v are in general different, since g_i and gⁱ are generally different.

When using curvilinear components, one can contract indices (i.e., sum on repeated indices) only on a superscript and a subscript, never on two superscripts or two subscripts. It is only for Cartesian coordinate systems, in which g_i = gⁱ, that the distinction between vⁱ and v_i disappears, and all indices can be written as subscripts, and summation can be performed on two subscripts.

2.6.2 Physical components

Since g_i and gⁱ in general have dimensions, the components vⁱ and v_i of the vector v do not in general have the dimensions of v itself. For instance, if we regard v as the velocity at position x, then, in our cylindrical polar example, v¹ and v³ have the dimensions of velocity (length/time) since g₁ and g₃ are dimensionless, but v² has dimensions of 1/time since g₂ has dimensions of length. Similarly, v₁ and v₃ are dimensionless, but v₂ has dimensions of (length)²/time.

From vⁱ or v_i we can produce the physical components of velocity v. Physical components of a vector or tensor have the same dimensional units as the vector or tensor itself. They are obtained by first defining unit vectors along the directions of g_i or gⁱ. Physical components are usually employed only in orthogonal coordinate systems.

Problem 2.60

For the cylindrical polar coordinate system (r, θ, z), determine the relations between the physical components v_r, v_θ, v_z, the covariant components v₁, v₂, v₃, and the contravariant components v¹, v², v³ of the vector v.

Solution

We define the unit vectors e_r, e_θ, e_z along the directions of g₁, g₂, g₃:

$\begin{array}{l} e_{r} \equiv cos θ e_{1} + sin θ e_{2} = g_{1}, \\ e_{θ} \equiv - sin θ e_{1} + cos θ e_{2} = \frac{g_{2}}{| g_{2} |} = \frac{1}{r} g_{2}, \\ e_{z} \equiv e_{3} = g_{3} . \end{array}$

si248_e (a)

Then

$\begin{array}{l} g^{1} = g_{1} = e_{r}, \\ g^{2} = \frac{1}{r^{2}} g_{2} = \frac{1}{r} e_{θ}, \\ g^{3} = g_{3} = e_{z} . \end{array}$

si249_e (b)

The vector v can then be expressed in terms of the physical components v_r, v_θ, v_z along the unit vectors e_r, e_θ, e_z:

$v = v_{r} e_{r} + v_{θ} e_{θ} + v_{z} e_{z} .$

(c)

Note that in physical components, as in Cartesian components (which are a special case of physical components), we can dispense with the distinction between superscripts and subscripts. Using the relations (b) to compare (c) with (2.112a) and (2.112b), we see that

$v_{r} = v^{1} = v_{1}, v_{θ} = r v^{2} = \frac{1}{r} v_{2} v_{z} = v^{3} = v_{3} .$

si251_e (d)

Problem 2.61

For the cylindrical polar coordinate system, determine the relations between the physical components and the contravariant components of the tensor T.

Solution

We write the tensor T in terms of its contravariant components by expanding (2.113a):

$T = T^{11} g_{1} \otimes g_{1} + T^{12} g_{1} \otimes g_{2} + T^{13} g_{1} \otimes g_{3} + T^{21} g_{2} \otimes g_{1} + T^{22} g_{2} \otimes g_{2} + T^{23} g_{2} \otimes g_{3} + T^{31} g_{3} \otimes g_{1} + T^{32} g_{3} \otimes g_{2} + T^{33} g_{3} \otimes g_{3} .$

(a)

The tensor T can also be written in terms of its physical cylindrical polar components as

$T = T_{rr} e_{r} \otimes e_{r} + T_{r θ} e_{r} \otimes e_{θ} + T_{rz} e_{r} \otimes e_{z} + T_{θ r} e_{θ} \otimes e_{r} + T_{θ θ} e_{θ} \otimes e_{θ} + T_{θ z} e_{θ} \otimes e_{z} + T_{zr} e_{z} \otimes e_{r} + T_{z θ} e_{z} \otimes e_{θ} + T_{zz} e_{z} \otimes e_{z} .$

(b)

Using the relations (b) in Problem 2.60 between e_r, e_θ, e_z and g₁, g₂, g₃, we compare (a) and (b) and conclude that

$\begin{array}{l} T^{11} = T_{rr}, & T^{12} = \frac{1}{r} T_{r θ}, & T^{13} = T_{rz}, \\ T^{21} = \frac{1}{r} T_{θ r}, & T^{22} = \frac{1}{r^{2}} T_{θ θ}, & T^{23} = \frac{1}{r} T_{θ z}, \\ T^{31} = T_{zr}, & T^{32} = \frac{1}{r} T_{z θ}, & T^{33} = T_{zz} . \end{array}$

si500_e (c)

2.6.3 Spatial derivatives: covariant differentiation

Since the basis vectors g_i are not fixed in space, their spatial derivatives are not zero. Consider the change of the basis vector g_i as one proceeds along the θ^j coordinate curve. This change in magnitude and direction, denoted by

$\frac{\partial g_{i}}{\partial θ^{j}} = change of g_{i} along θ^{j} curve,$

si501_e

is itself a vector, and therefore can be expressed in terms of the basis {g_i}:

$\frac{\partial g_{i}}{\partial θ^{j}} = Γ_{ij}^{k} g_{k} = Γ_{ij}^{1} g_{1} + Γ_{ij}^{2} g_{2} + Γ_{ij}^{3} g_{3} .$

si502_e (2.114)

The coefficients Γ_ij^k in (2.114) are called Christoffel symbols of the second kind. From the definition (2.114), it follows that

$\frac{\partial g^{i}}{\partial θ^{j}} = - Γ_{kj}^{i} g^{k} .$

si503_e (2.115)

2.6.3.1 Gradient and divergence of a vector

The spatial derivative of a vector-valued function v of position x, when expressed with respect to the basis vectors g_i, must take into account the possible spatial dependence of both the coefficients vⁱ and the basis {g_i}:

$\begin{array}{l} grad v = \frac{\partial v}{\partial x} & = \frac{\partial}{\partial x} (v^{i} g_{i}) \\ = \frac{\partial}{\partial θ^{j}} (v^{i} g_{i}) \otimes g^{j} \\ = \frac{\partial v^{i}}{\partial θ^{j}} g_{i} \otimes g^{j} + v^{i} \frac{\partial g_{i}}{\partial θ^{j}} \otimes g^{j} \\ = \frac{\partial v^{i}}{\partial θ^{j}} g_{i} \otimes g^{j} + v^{i} Γ_{ij}^{k} g_{k} \otimes g^{j} \\ = \frac{\partial v^{i}}{\partial θ^{j}} g_{i} \otimes g^{j} + v^{m} Γ_{mj}^{i} g_{i} \otimes g^{j} \\ = (\frac{\partial v^{i}}{\partial θ^{j}} + Γ_{mj}^{i} v^{m}) g_{i} \otimes g^{j} . \end{array}$

si504_e (2.116)

The coefficient $\frac{\partial v^{i}}{\partial θ^{j}} + Γ_{mj}^{i} v^{m}$ si505_e is called the covariant derivative of vⁱ, and is often denoted by ${v^{i} |}_{j}$ or ${v^{i} ‖}_{j}$ . Similarly, it can be shown that

$grad v = \frac{\partial v}{\partial x} = (\frac{\partial v_{i}}{\partial θ^{j}} - Γ_{ij}^{m} v_{m}) g^{i} \otimes g^{j} .$

(2.117)

With use of definition (2.97), the divergence of a vector v in curvilinear coordinates is given by

$\begin{array}{l} div v & \equiv tr (grad v) \\ = (\frac{\partial v^{i}}{\partial θ^{j}} + Γ_{mj}^{i} v^{m}) tr (g_{i} \otimes g^{j}) \\ = (\frac{\partial v^{i}}{\partial θ^{j}} + Γ_{mj}^{i} v^{m}) g_{i} \cdot\cdot g^{j} \\ = \frac{\partial v^{i}}{\partial θ^{i}} + Γ_{mi}^{i} v^{m} . \end{array}$

si509_e (2.118)

In can be shown (refer to Problem 2.63) that for the special case of cylindrical polar coordinates (r, θ, z), we have

$grad v = [\begin{matrix} \frac{\partial v_{r}}{\partial r} & \frac{1}{r} \frac{\partial v_{r}}{\partial θ} - \frac{v_{θ}}{r} & \frac{\partial v_{r}}{\partial z} \\ \frac{\partial v_{θ}}{\partial r} & \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{v_{r}}{r} & \frac{\partial v_{θ}}{\partial z} \\ \frac{\partial v_{z}}{\partial r} & \frac{1}{r} \frac{\partial v_{z}}{\partial θ} & \frac{\partial v_{z}}{\partial z} \end{matrix}]$

si510_e (2.119)

and (refer to Problem 2.64)

$div v = \frac{\partial v_{r}}{\partial r} + \frac{v_{r}}{r} + \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{\partial v_{z}}{\partial z} .$

si511_e (2.120)

In spherical coordinates (r, θ, φ), where θ is the polar angle and φ is the azimuthal angle, we have

$grad v = [\begin{matrix} \frac{\partial v_{r}}{\partial r} & \frac{1}{r} \frac{\partial v_{r}}{\partial θ} - \frac{v_{θ}}{r} & \frac{1}{r sin θ} \frac{\partial v_{r}}{\partial φ} - \frac{v_{φ}}{r} \\ \frac{\partial v_{θ}}{\partial r} & \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{v_{r}}{r} & \frac{1}{r sin θ} \frac{\partial v_{θ}}{\partial φ} - \frac{cot θ}{r} v_{φ} \\ \frac{\partial v_{φ}}{\partial r} & \frac{1}{r} \frac{\partial v_{φ}}{\partial θ} & \frac{1}{r sin θ} \frac{\partial v_{φ}}{\partial φ} + \frac{v_{r}}{r} + \frac{cot θ}{r} v_{θ} \end{matrix}]$

si512_e (2.121)

and

$div v = \frac{\partial v_{r}}{\partial r} + \frac{2 v_{r}}{r} + \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{cot θ}{r} v_{θ} + \frac{1}{r sin θ} \frac{\partial v_{φ}}{\partial φ} .$

si513_e (2.122)

Problem 2.62

Determine the Christoffel symbols Γ^k_ij in the cylindrical polar coordinate system (r, θ, z).

Solution

Recall from (c) in Problem 2.64 that the covariant basis of a cylindrical polar coordinate system (θ¹ = r, θ² = θ, θ³ = z) is

$g_{1} = cos θ e_{1} + sin θ e_{2}, g_{2} = - r sin θ e_{1} + r cos θ e_{2}, g_{3} = e_{3} .$

It follows that

$\frac{\partial g_{1}}{\partial θ^{1}} = \frac{\partial}{\partial r} (cos θ e_{1} + sin θ e_{2}) = 0$

si515_e

so, by (2.114),

$\begin{matrix} Γ_{11}^{1} = Γ_{11}^{2} = Γ_{11}^{3} = 0; \\ \frac{\partial g_{1}}{\partial θ^{2}} = \frac{\partial}{\partial θ} (cos θ e_{1} + sin θ e_{2}) = - sin θ e_{1} + cos θ e_{2} = e_{θ} = \frac{1}{r} g_{2}, \end{matrix}$

si516_e

$\begin{matrix} Γ_{12}^{1} = Γ_{12}^{3} = 0, Γ_{11}^{2} = \frac{1}{r}; \\ \frac{\partial g_{2}}{\partial θ^{1}} = \frac{\partial}{\partial r} (- r sin θ e_{1} + r cos θ e_{2}) = - sin θ e_{1} + cos θ e_{2} = \frac{1}{r} g_{2}, \end{matrix}$

si517_e

$Γ_{21}^{1} = Γ_{21}^{3} = 0, Γ_{21}^{2} = \frac{1}{r};$

si518_e

and

$\frac{\partial g_{2}}{\partial θ^{2}} = \frac{\partial}{\partial θ} (- r sin θ e_{1} + r cos θ e_{2}) = - r (cos θ e_{1} + sin θ e_{2}) = - r g_{1},$

si519_e

$Γ_{22}^{1} = - r, Γ_{22}^{2} = Γ_{22}^{3} = 0 .$

Also,

$\frac{\partial g_{1}}{\partial θ^{3}} = \frac{\partial g_{2}}{\partial θ^{3}} = \frac{\partial g_{3}}{\partial θ^{1}} = \frac{\partial g_{3}}{\partial θ^{2}} = \frac{\partial g_{3}}{\partial θ^{3}} = 0,$

si521_e

$Γ_{3 k}^{i} = Γ_{j 3}^{i} = 0 .$

Therefore, the only nonzero Christoffel symbols in the cylindrical polar coordinate system are

$Γ_{12}^{2} = Γ_{21}^{2} = \frac{1}{r}, Γ_{22}^{1} = - r .$

si523_e (a)

Problem 2.63

Determine grad v in cylindrical polar coordinates.

Solution

Recall from (2.116) that

$grad v = (\frac{\partial v^{i}}{\partial θ^{j}} + Γ_{mj}^{i} v^{m}) g_{i} \otimes g^{j} .$

si252_e

Then, using (b) and (d) in Problem 2.66 and (a) in Problem 2.68 we can determine the expression for grad v in physical cylindrical polar coordinates:

$\begin{array}{l} (i, j = 1, 1) & \Rightarrow (\frac{\partial v^{1}}{\partial θ^{1}} + 0) g_{1} \otimes g^{1} = \frac{\partial v_{r}}{\partial r} e_{r} \otimes e_{r}, \\ (i, j = 1, 2) & \Rightarrow (\frac{\partial v^{1}}{\partial θ^{2}} + Γ_{22}^{1} v^{2}) g_{1} \otimes g^{2} = [\frac{\partial v_{r}}{\partial θ} - r (\frac{v_{θ}}{r})] e_{r} \otimes \frac{1}{r} e_{θ} = (\frac{1}{r} \frac{\partial v_{r}}{\partial θ} - \frac{v_{θ}}{r}) e_{r} \otimes e_{θ}, \\ (i, j = 1, 3) & \Rightarrow (\frac{\partial v^{1}}{\partial θ^{3}} + 0) g_{1} \otimes g^{3} = \frac{\partial v_{r}}{\partial z} e_{r} \otimes e_{z}, \\ (i, j = 2, 1) & \Rightarrow (\frac{\partial v^{2}}{\partial θ^{1}} + Γ_{21}^{2} v^{2}) g_{2} \otimes g^{1} = [\frac{\partial}{\partial r} (\frac{v_{θ}}{r}) + \frac{1}{r} (\frac{v_{θ}}{r})] r e_{θ} \otimes e_{r} = (\frac{1}{r} \frac{\partial v_{θ}}{\partial r} - \frac{v_{θ}}{r^{2}} + \frac{v_{θ}}{r^{2}}) r e_{θ} \otimes e_{r} = \frac{\partial v_{θ}}{\partial r} e_{θ} \otimes e_{r}, \\ (i, j = 2, 2) & \Rightarrow (\frac{\partial v^{2}}{\partial θ^{2}} + Γ_{12}^{2} v^{1}) g_{2} \otimes g^{2} = [\frac{\partial}{\partial θ} (\frac{v_{θ}}{r}) + \frac{1}{r} v_{r}] r e_{θ} \otimes \frac{1}{r} e_{θ} = (\frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{v_{r}}{r}) e_{θ} \otimes e_{θ}, \\ (i, j = 2, 3) & \Rightarrow (\frac{\partial v^{2}}{\partial θ^{3}} + 0) g_{2} \otimes g^{3} = \frac{\partial}{\partial z} (\frac{v_{θ}}{r}) r e_{θ} \otimes e_{z} = \frac{\partial v_{θ}}{\partial z} e_{θ} \otimes e_{z}, \\ (i, j = 3, 1) & \Rightarrow (\frac{\partial v^{3}}{\partial θ^{1}} + 0) g_{3} \otimes g^{1} = \frac{\partial v_{z}}{\partial r} e_{z} \otimes e_{r}, \\ (i, j = 3, 2) & \Rightarrow (\frac{\partial v^{3}}{\partial θ^{2}} + 0) g_{3} \otimes g^{2} = \frac{1}{r} \frac{\partial v_{z}}{\partial θ} e_{z} \otimes e_{θ}, \\ (i, j = 3, 3) & \Rightarrow (\frac{\partial v^{3}}{\partial θ^{3}} + 0) g_{3} \otimes g^{3} = \frac{\partial v_{z}}{\partial z} e_{z} \otimes e_{z} . \end{array}$

si253_e

Thus, we have

$grad v = \frac{\partial v_{r}}{\partial r} e_{r} \otimes e_{r} + (\frac{1}{r} \frac{\partial v_{r}}{\partial θ} - \frac{v_{θ}}{r}) e_{r} \otimes e_{θ} + \frac{\partial v_{r}}{\partial z} e_{r} \otimes e_{z} + \frac{\partial v_{θ}}{\partial r} e_{θ} \otimes e_{r} + (\frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{v_{r}}{r}) e_{θ} \otimes e_{θ} + \frac{\partial v_{θ}}{\partial z} e_{θ} \otimes e_{z} + \frac{\partial v_{z}}{\partial r} e_{z} \otimes e_{r} + \frac{1}{r} \frac{\partial v_{z}}{\partial θ} e_{z} \otimes e_{θ} + \frac{\partial v_{z}}{\partial z} e_{z} \otimes e_{z}$

si254_e

or, in matrix form,

$[grad v] = [\begin{matrix} \frac{\partial v_{r}}{\partial r} & \frac{1}{r} \frac{\partial v_{r}}{\partial θ} - \frac{v_{θ}}{r} & \frac{\partial v_{r}}{\partial z} \\ \frac{\partial v_{θ}}{\partial r} & \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{v_{r}}{r} & \frac{\partial v_{θ}}{\partial z} \\ \frac{\partial v_{z}}{\partial r} & \frac{1}{r} \frac{\partial v_{z}}{\partial θ} & \frac{\partial v_{z}}{\partial z} \end{matrix}] .$

si255_e

Problem 2.64

Determine div v in cylindrical polar coordinates.

Solution

Recall from (2.118) that

$div v = \frac{\partial v^{i}}{\partial θ^{i}} + Γ_{mi}^{i} v^{m} .$

si256_e

Expanding this, we have

$div v = \frac{\partial v^{1}}{\partial θ^{1}} + \frac{\partial v^{2}}{\partial θ^{2}} + \frac{\partial v^{3}}{\partial θ^{3}} + Γ_{11}^{1} v^{1} + Γ_{12}^{2} v^{1} + \dots .$

si257_e

Then, with use of (d) in Problem 2.66 and (a) in Problem 2.68 this becomes

$div v = \frac{\partial v_{r}}{\partial r} + \frac{\partial}{\partial θ} (\frac{v_{θ}}{r}) + \frac{\partial v_{z}}{\partial z} + \frac{1}{r} v_{r} = \frac{\partial v_{r}}{\partial r} + \frac{v_{r}}{r} + \frac{1}{r} \frac{\partial v_{θ}}{\partial θ} + \frac{\partial v_{z}}{\partial z} .$

si258_e

Problem 2.65

Determine div T in cylindrical polar coordinates.

Solution

It follows from (2.124) that

$div T = (\frac{\partial T^{11}}{\partial θ^{1}} + \frac{\partial T^{12}}{\partial θ^{2}} + \frac{\partial T^{13}}{\partial θ^{3}} + Γ_{22}^{1} T^{22} + Γ_{12}^{2} T^{11} + \dots) g_{1} + (\frac{\partial T^{21}}{\partial θ^{1}} + \frac{\partial T^{22}}{\partial θ^{2}} + \frac{\partial T^{23}}{\partial θ^{3}} + Γ_{22}^{2} T^{12} + Γ_{21}^{2} T^{21} + Γ_{12}^{2} T^{21} + \dots) g_{2} + (\frac{\partial T^{31}}{\partial θ^{1}} + \frac{\partial T^{32}}{\partial θ^{2}} + \frac{\partial T^{33}}{\partial θ^{3}} + Γ_{12}^{2} T^{31} + \dots) g_{3} .$

si259_e

Using (b) in Problem 2.66, (c) in Problem 2.67, and (a) in Problem 2.68 we have

$\begin{array}{l} div T & = [\frac{\partial T_{rr}}{\partial r} + \frac{\partial}{\partial θ} (\frac{1}{r} T_{r θ}) + \frac{\partial T_{rz}}{\partial z} - r \frac{1}{r^{2}} T_{θ θ} + \frac{1}{r} T_{rr}] e_{r} + [\frac{\partial}{\partial r} (\frac{1}{r} T_{θ r}) + \frac{\partial}{\partial θ} (\frac{1}{r^{2}} T_{θ θ}) + \frac{\partial}{\partial z} (\frac{1}{r} T_{θ z}) + \frac{1}{r} (\frac{1}{r} T_{r θ} + \frac{2}{r} T_{θ r})] r e_{θ} + [\frac{\partial T_{zr}}{\partial r} + \frac{\partial}{\partial θ} (\frac{1}{r} T_{z θ}) + \frac{\partial T_{zz}}{\partial z} + \frac{1}{r} T_{zr}] e_{z} \\ = [\frac{\partial T_{rr}}{\partial r} + \frac{1}{r} \frac{\partial T_{r θ}}{\partial θ} + \frac{\partial T_{rz}}{\partial z} - \frac{1}{r} (T_{rr} - T_{θ θ})] e_{r} + [\frac{\partial T_{θ r}}{\partial r} + \frac{1}{r} \frac{\partial T_{θ θ}}{\partial θ} + \frac{\partial T_{θ z}}{\partial z} + \frac{1}{r} (T_{r θ} + T_{θ r})] e_{θ} + [\frac{\partial T_{zr}}{\partial r} + \frac{1}{r} \frac{\partial T_{z θ}}{\partial θ} + \frac{\partial T_{zz}}{\partial z} + \frac{1}{r} T_{zr}] e_{z} . \end{array}$

si260_e

2.6.3.2 Divergence of a tensor

Recall the definition (2.98) of the divergence of a tensor T:

$(div T) \cdot a = div (T^{T} a)$

for any vector a in $ε^{3}$ . For a = constant, we have

$\frac{\partial a}{\partial x} = 0,$

or, in curvilinear coordinates,

$\frac{\partial}{\partial θ^{j}} (a_{i} g^{i}) \otimes g^{j} = (\frac{\partial a_{i}}{\partial θ^{j}} - Γ_{ij}^{m} a_{m}) g^{i} \otimes g^{j} = 0,$

si527_e

which implies

$\frac{\partial a_{i}}{\partial θ^{j}} = Γ_{ij}^{m} a_{m}$

si528_e (2.123)

for a = constant. The right-hand side of (2.98) becomes in curvilinear coordinates

$\begin{array}{l} div (T^{T} a) & = div [(T^{ji} g_{i} \otimes g_{j}) a_{k} g^{k}] \\ = div [T^{ji} a_{k} (g_{j} \otimes g^{k}) g_{i}] \\ = div [T^{ji} a_{j} g_{i}] \\ = \frac{\partial}{\partial θ^{i}} (T^{ji} a_{j}) + Γ_{mi}^{i} T^{jm} a_{j} \\ = \frac{\partial T^{ji}}{\partial θ^{i}} a_{j} + T^{ji} \frac{\partial a_{j}}{\partial θ^{i}} + Γ_{mi}^{i} T^{jm} a_{j} . \end{array}$

si529_e

With use of (2.123), this becomes

$div (T^{T} a) = \frac{\partial T^{ji}}{\partial θ^{i}} a_{j} + T^{ji} Γ_{ji}^{m} a_{m} + Γ_{mi}^{i} T^{jm} a_{j} = (\frac{\partial T^{ji}}{\partial θ^{i}} + Γ_{mi}^{j} T^{mi} + Γ_{mi}^{i} T^{jm}) a_{j},$

si530_e

so (2.98) in curvilinear coordinates is

$(div T) \cdot g^{j} a_{j} = (\frac{\partial T^{ji}}{\partial θ^{i}} + Γ_{mi}^{j} T^{mi} + Γ_{mi}^{i} T^{jm}) a_{j} .$

si531_e

Therefore,

$div T = (\frac{\partial T^{ij}}{\partial θ^{j}} + Γ_{mj}^{i} T^{mj} + Γ_{mj}^{j} T^{im}) g_{i} .$

si532_e (2.124)

It can be shown (refer to Problem 2.65) that for the special case of cylindrical polar coordinates (r, θ, z), (2.124) becomes

$div T = [\frac{\partial T_{rr}}{\partial r} + \frac{1}{r} \frac{\partial T_{r θ}}{\partial θ} + \frac{\partial T_{rz}}{\partial z} + \frac{1}{r} (T_{rr} - T_{θ θ})] e_{r} + [\frac{\partial T_{θ r}}{\partial r} + \frac{1}{r} \frac{\partial T_{θ θ}}{\partial θ} + \frac{\partial T_{θ z}}{\partial z} + \frac{1}{r} (T_{r θ} - T_{θ r})] e_{θ} + [\frac{\partial T_{zr}}{\partial r} + \frac{1}{r} \frac{\partial T_{z θ}}{\partial θ} + \frac{\partial T_{zz}}{\partial z} + \frac{1}{r} T_{zr}] e_{z} .$

si533_e (2.125)

In spherical coordinates (r, θ, φ), we have

$div T = [\frac{\partial T_{rr}}{\partial r} + \frac{1}{r} \frac{\partial T_{r θ}}{\partial θ} + \frac{1}{r sin θ} \frac{\partial T_{r φ}}{\partial φ} + \frac{1}{r} (2 T_{rr} - T_{θ θ} - T_{φ φ}) + \frac{cot θ}{r} T_{r θ}] e_{r} + [\frac{\partial T_{θ r}}{\partial r} + \frac{1}{r} \frac{\partial T_{θ θ}}{\partial θ} + \frac{1}{r sin θ} \frac{\partial T_{θ φ}}{\partial φ} + \frac{1}{r} (T_{r θ} - 2 T_{θ r}) + \frac{cot θ}{r} (T_{θ θ} - T_{φ φ})] e_{θ} + [\frac{\partial T_{φ r}}{\partial r} + \frac{1}{r} \frac{\partial T_{φ θ}}{\partial θ} + \frac{1}{r sin θ} \frac{\partial T_{φ φ}}{\partial φ} + \frac{1}{r} (T_{r φ} + 2 T_{φ r}) + \frac{cot θ}{r} (T_{θ φ} - T_{φ θ})] e_{φ} .$

si534_e (2.126)

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 2.6 Curvilinear coordinates

Create new playlist

Sign In

Sign Up

2.6 Curvilinear coordinates

2.6.1 Covariant and contravariant basis vectors

2.6.2 Physical components

2.6.3 Spatial derivatives: covariant differentiation

2.6.3.1 Gradient and divergence of a vector

2.6.3.2 Divergence of a tensor

Table of Contents for
2.6 Curvilinear coordinates