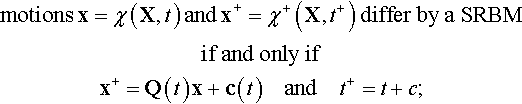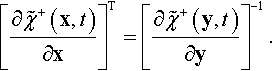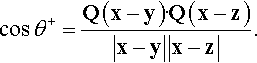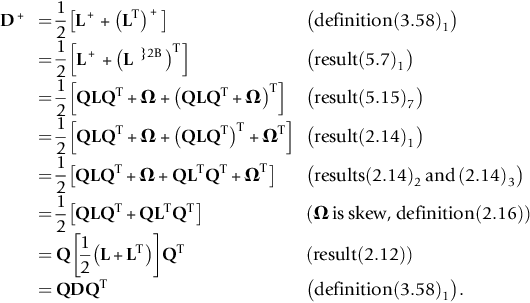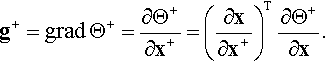Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 5

Constitutive Modeling in Mechanics and Thermomechanics

Abstract

The constitutive equations for a particular material, together with the conservation laws of mass, linear momentum, angular momentum, and energy, govern the response of that material. Unlike the conservation laws, however, the constitutive equations vary from material to material. In other words, they depend on the physical behavior of the particular material being modeled. In this chapter, we provide a broad overview of constitutive modeling in mechanics and thermomechanics. We describe how the constitutive equations must satisfy the second law of thermodynamics, conservation of angular momentum, material symmetry requirements, and invariance under superposed rigid body motions. Special attention is devoted to determining how various kinematic, kinetic, and thermodynamic quantities transform under a superposed rigid body motion and, in turn, how these transformations can be used to develop appropriate invariance requirements. We also examine useful thermodynamic concepts in constitutive modeling, such as thermomechanical processes and Legendre transformations.

Keywords

constitutive modeling

constitutive equations

response functions

invariance

material symmetry

thermomechanical process

Legendre transformation

Part I: Mechanics

5.1 Fundamental laws, constitutive equations, a well-posed initial-value boundary-value problem

Recall from Chapter 4 that the field equations, i.e., those equations that must be satisfied at each location and time in the domain of interest, are, in the mechanical theory,

$ρ^{'} + v \cdot grad ρ + ρ div v = 0,$

(5.1)

$div T + ρ b = ρ [v^{'} + (grad v) v],$

(5.2)

$T = T^{T} .$

(5.3)

Equations (5.1)–(5.3) are the local Eulerian forms of conservation of mass, conservation of linear momentum, and conservation of angular momentum, respectively. In this form, the density ρ, velocity v, and Cauchy stress T are scalar, vector, and tensor functions, respectively, of present position x and time t. Note that in the mechanical theory (sometimes referred to as the isothermal, or constant temperature, theory), we do not concern ourselves with the thermal quantities of temperature Θ, entropy η, heat flux h, and heat supply r, nor the first and second laws of thermodynamics. Recall from Chapter 3 the definitions of the partial derivatives ρ′, grad ρ, grad v, div v, and div T appearing in (5.1)–(5.3), e.g.,

$ρ^{'} = \frac{\partial}{\partial t} \tilde{ρ} (x, t), grad ρ = \frac{\partial}{\partial x} \tilde{ρ} (x, t), grad v \frac{\partial}{\partial x} \tilde{v} (x, t) .$

si89_e

The field equations (5.1)–(5.3) must be satisfied at all locations x in the open region $R$ of $E^{3}$ occupied by the body in the present configuration at each time t, for all time t in the interval of interest. In Cartesian component notation, (5.1)–(5.3) consist of seven coupled nonlinear partial differential equations (PDEs) for the 13 scalar functions ρ, v₁, v₂, v₃, T₁₁, T₁₂, T₁₃, T₂₁, T₂₂, T₂₃, T₃₁, T₃₂, and T₃₃ of the independent variables x₁, x₂, x₃, and t. To close this system of field equations (i.e., to have the same number of unknowns as equations, which is necessary for a well-posed initial-value boundary-value problem formulation), there must be six additional scalar equations.

These six scalar equations, called constitutive equations, depend on the physical behavior of the particular material being modeled. (In contrast, the field equations (5.1)–(5.3) are valid for all continua.) In general, different materials will have different constitutive equations. The constitutive equations proposed for a specific material or class of materials must be grounded on physical experiments.

In the Eulerian formulation, the six scalar constitutive equations are a single tensor equation relating the stress T to the motion χ (and possibly rates, gradients, or the history of the motion). In general, the stress T at time t can depend on the entire history of motion up to time t; for practical models, however, this dependence is reduced to manageable limits, while still including enough dependence to be physically useful. The tensorial constitutive equation defines the response of the continuum to the motion, and is therefore also called the response function of the continuum. In general, different materials have different responses to the same motion, and are thus characterized by different constitutive equations.

The tensor constitutive equation relating T to the motion must be consistent with conservation of angular momentum (5.3), so it must be symmetric in T. Therefore, although the tensor constitutive equation corresponds to nine scalar equations, only six of these are independent, since we must have T₂₁ = T₁₂, T₃₁ = T₁₃, and T₃₂ = T₂₃. By counting equations, we see that these six independent constitutive equations are the field equations necessary to close the set (5.1)–(5.3): the six constitutive equations plus (5.1)–(5.3) are 13 coupled nonlinear PDEs for the 13 functions of x₁, x₂, x₃, and t listed previously.

With the constitutive equations given and the set of equations closed, to complete a well-posed initial-value boundary-value problem formulation, it is necessary to specify the appropriate initial conditions and boundary conditions. The initial conditions and boundary conditions necessary in a particular problem depend on the differential operators present in the constitutive equation, as well as the differential operators appearing in the field equations (5.1) and (5.2). For instance, since first-order time derivatives of ρ and v appear in (5.1) and (5.2), it is necessary to give initial values of ρ and v throughout the domain. Initial conditions on ρ′ and v′, etc., will be necessary if there are higher-order time derivatives in the constitutive equations; see Table 5.1.

Table 5.1

Eulerian Formulation of the Mechanical Initial-Value Boundary-Value Problem

Domain	All $x \in R (t)$ , the region occupied by the body in the present configuration at time t
Time interval	t_o ≤ t ≤ t_f
	ρ′ + v · grad ρ + ρ div v = 0
Governing equations	div T + ρb = ρ[v′ + (grad v) v]
	$T = \overset{˘}{T} (motion)$ satisfying T = T^T
Specified functions	$b = \tilde{b} (x, t)$ specified for all $x \in R (t)$ , t_o ≤ t ≤ t_f
Unknowns	$\tilde{ρ} (x, t)$ , $\tilde{v} (x, t)$ , $\tilde{T} (x, t)$
Initial conditions	Specified at t = t_o for all $x \in R (t_{o})$
Boundary conditions	Specified on $x \in \partial R (t)$ for t_o ≤ t ≤ t_f

The Lagrangian formulation of the mechanical theory differs from the Eulerian formulation in that (1) it has different unknowns, (2) it has different differential operators in the field equations and hence different initial and boundary conditions, and (3) the concept of a reference configuration requires that information be supplied about the reference state. The independent variables in the Lagrangian formulation are reference position X and time t; see Table 5.2.

Table 5.2

Lagrangian Formulation of the Mechanical Initial-Value Boundary-Value Problem

Domain	All $X \in R_{R}$ , the region occupied by the body in the reference configuration
Time interval	t_o ≤ t ≤ t_f
	ρJ = ρ_R
Governing equations	$Div P + ρ_{R} b = ρ_{R} \ddot{χ}$
	$P = \overset{˘}{P} (motion)$ satisfying PF^T = FP^T
Specified functions	$b = \hat{b} (X, t)$ specified for all $X \in R_{R}$ , t_o ≤ t ≤ t_f
	$ρ_{R} = {\hat{ρ}}_{R} (X)$ specified for all $X \in R_{R}$
Unknowns	$\hat{ρ} (X, t)$ , χ(X, t), $\hat{P} (X, t)$
Initial conditions	Specified at t = t_o for all $X \in R_{R}$
Boundary conditions	Specified on $X \in \partial R_{R}$ for t_o ≤ t ≤ t_f

Exercises

1. Write the field equations (5.1)–(5.3) in indicial notation. Then fully expand them into their Cartesian component forms. Verify that the resulting system of equations consists of seven scalar PDEs for 13 scalar unknowns.

5.2 Restrictions on the constitutive equations

As discussed in Section 5.1, the tensor constitutive equation relating the Cauchy stress T to the motion χ must satisfy conservation of angular momentum. Additionally, it must satisfy invariance requirements, and perhaps some material symmetry conditions. These restrictions will prove useful. For instance, in Chapter 7, we will show how these restrictions allow us to reduce a proposed form of the constitutive equation for viscous fluids. Such reductions are welcomed since they allow the fluid to be characterized with fewer laboratory experiments.

5.2.1 Invariance under superposed rigid body motions

In this book, we require that the constitutive equation for the Cauchy stress T be invariant under all possible superposed rigid body motions (SRBMs) of the body. (Refer to Appendix A for other notions of invariance.) Invariance under SRBMs demands that if two motions of a body composed of the same material differ only by a SRBM, then physically the internal response generated in the two motions must be the same, apart from orientation. The response due to the SRBM should be zero. If it is not, the proposed constitutive equation is not physical.

5.2.1.1 Superposed rigid body motions

Consider two motions, given by the functions x = χ(X, t) and x⁺ = χ⁺(X, t⁺), both referred to the same reference configuration. A particle at reference position X is mapped by motion χ to position x at time t; this same particle at reference position X is mapped by motion χ⁺ to position x⁺ at time t⁺. Another particle, at position Y in the reference configuration, is mapped by motion χ to position y at time t, and by motion χ⁺ to position y⁺ at time t⁺; see Figure 5.1. The motions χ and χ⁺ differ by a SRBM if

f05-01-9780123946003 — Figure 5.1 Two motions χ and χ⁺ that differ by a SRBM.

(1) the elapsed time between an arbitrary pair of instants (or events) t₁ and t₂, and t⁺₁ and t⁺₂, is the same,

(2) the order in which two distinct instants t₁ and t₂, and t⁺₁ and t⁺₂, occur is the same, and

(3) the distance between an arbitrary pair of particles x and y, and x⁺ and y⁺, at any particular instant is the same.

Necessary and sufficient conditions that the two motions x = χ(X, t) and x⁺ = χ⁺(X, t⁺) differ by a SRBM are that x⁺ and t⁺ are related to x and t by

$x^{+} = Q (t) x + c (t),$

(5.4a)

$t^{+} = t + c,$

(5.4b)

where Q(t) is a proper orthogonal tensor-valued function of time t, c(t) is a vector-valued function of time t, and c is a scalar constant. (Refer to Section 2.2.6 for a discussion of proper orthogonal tensors.) Said differently,

$\begin{matrix} motions x = χ (X, t) and x^{+} = χ^{+} (X, t^{+}) differ by a SRBM \\ if and only if \\ x^{+} = Q (t) x + c (t) and t^{+} = t + c; \end{matrix}$

si94_e (5.5)

refer to Problem 5.1. Physically, the proper orthogonal tensor Q(t) can be interpreted as a rigid body rotation, and the vector c(t) can be interpreted as a rigid body translation. Note that the linear equation (5.4a) can be inverted, i.e.,

$x = Q^{T} (t) x^{+} - Q^{T} (t) c (t),$

$\frac{\partial x}{\partial x^{+}} = Q^{T} .$

si96_e (5.6)

Also, we can verify that

${(A^{T})}^{+} = {(A^{+})}^{T}, {(A^{- 1})}^{+} = {(A^{+})}^{- 1}, {(\dot{A})}^{+} = \dot{\bar{A^{+}}}$

(5.7)

for any tensor A.

Problem 5.1

Prove that motions x = χ(X, t) and x⁺ = χ⁺(X, t⁺) differ by a SRBM if and only if

$x^{+} = Q (t) x + c (t) and t^{+} = t + c .$

Solution

To prove necessity, we must show that if two motions x = χ(X, t) and x⁺ = χ⁺(X, t⁺) differ by a SRBM, then

$x^{+} = Q (t) x + c (t) and t^{+} = t + c$

for all proper orthogonal Q(t). In other words, we must show that requirements (1)-(3) discussed in Section 5.2.1.1 imply (5.4a) and (5.4b).

Requirements (1) and (2) demand that t⁺ = t + c, i.e., the two time scales differ only by their choice of an origin, so we have shown (5.4b). We now show that requirement (3) implies (5.4a).

At time t, a particle in the one motion occupies position x, given by the function

$x = χ (X, t) .$

At corresponding instant t⁺ = t + c in the other motion, the same particle occupies position x⁺, given by the function

$x^{+} = χ^{+} (X, t^{+}) .$

(a)

Another particle at time t in the first motion occupies position y, given by

$y = χ (Y, t),$

and at time t⁺ in the second motion occupies position y⁺, given by

$y^{+} = χ^{+} (Y, t^{+}) .$

(b)

To summarize, the motion χ takes the particles occupying reference positions X and Y to present positions x and y at time t, while the motion χ⁺ takes those same particles to present positions x⁺ and y⁺ at time t⁺. Recalling the inverse relation X = χ⁻¹(x, t) and using t⁺ = t + c, we may rewrite (a) as

$x^{+} = χ^{+} (X, t^{+}) = χ^{+} (χ^{- 1} (x, t), t + c) \equiv {\tilde{χ}}^{+} (x, t) .$

Similarly, (b) may be rewritten as

$y^{+} = {\tilde{χ}}^{+} (y, t) .$

Requirement (3) demands that the distance |x − y| between x and y at time t is the same as the distance |x⁺ − y⁺| between x⁺ and y⁺ at time t⁺ = t + c. This is equivalent to

$(x^{+} - y^{+}) \cdot (x^{+} - y^{+}) = (x - y) \cdot (x - y),$

$[{\tilde{χ}}^{+} (x, t) - {\tilde{χ}}^{+} (y, t)] \cdot [{\tilde{χ}}^{+} (x, t) - {\tilde{χ}}^{+} (y, t)] = (x - y) \cdot (x - y),$

(c)

for all x, y, and t. It follows from (2.99)₃ that differentiation of (c) with respect to x gives

$2 {[\frac{\partial {\tilde{χ}}^{+} (x, t)}{\partial x}]}^{T} [{\tilde{χ}}^{+} (x, t) - {\tilde{χ}}^{+} (y, t)] = 2 (x - y) .$

si31_e (d)

Then, differentiation of (d) with respect to y gives

$- 2 {[\frac{\partial {\tilde{χ}}^{+} (x, t)}{\partial x}]}^{T} [\frac{\partial {\tilde{χ}}^{+} (y, t)}{\partial y}] = - 2 I,$

si32_e

from which we deduce that

${[\frac{\partial {\tilde{χ}}^{+} (x, t)}{\partial x}]}^{T} = {[\frac{\partial {\tilde{χ}}^{+} (y, t)}{\partial y}]}^{- 1} .$

si33_e (e)

In (e) we have that a tensor-valued function of (y, t) is equal to a tensor-valued function of (x, t). Since x and y are independent, we deduce that both tensor-valued functions depend on t alone, i.e.,

$\frac{\partial {\tilde{χ}}^{+} (x, t)}{\partial x} = Q (t), \frac{\partial {\tilde{χ}}^{+} (y, t)}{\partial y} = Q (t),$

si34_e (f)

and thus, by (e),

$Q^{T} (t) = Q^{- 1} (t) .$

(g)

Equation (g) implies that Q(t) is orthogonal (refer to (2.51)), so det Q = ±1. However, the SRBM under consideration must include as a special case ${\tilde{χ}}^{+} (x, t) = x$ . For this particular case, Q = I and det Q = 1. Since motions are continuous, we must have det Q = 1 always, so Q(t) is proper orthogonal. The first-order PDE (f)₁ (or system of first-order PDEs in component form) can then be integrated to give

$x^{+} = {\tilde{χ}}^{+} (x, t) = Q (t) x + c (t),$

which is (5.4a). We have thus completed the necessity proof.

Now, to prove sufficiency, we must show that if

$x^{+} = Q (t) x + c (t) and t^{+} = t + c,$

with Q(t) proper orthogonal, then motions x = χ(X, t) and x⁺ = χ⁺(X, t⁺) differ by a SRBM. In other words, we must show that (5.4a) and (5.4b) imply conditions (1)-(3) discussed in Section 5.2.1.1.

Equation (5.4b) obviously implies requirements (1) and (2). From (5.4a), it follows that for any pair of particles,

$\begin{array}{l} {| x^{+} - y^{+} |}^{2} & = (x^{+} - y^{+}) \cdot (x^{+} - y^{+}) \\ = (Qx + c - Qy - c) \cdot (Qx + c - Qy - c) \\ = (Qx - Qy) \cdot (Qx - Qy) \\ = Q (x - y) \cdot Q (x - y) \\ = (x - y) \cdot (x - y) \\ = {| x - y |}^{2}, \end{array}$

si39_e

so the distance |x⁺ − y⁺| between x⁺ and y⁺ is the same as the distance |x − y| between x and y. Thus, requirement (3) is satisfied.

Exercises

1. Verify that for any tensor A,

(a) (A^T)⁺ = (A⁺)^T,

(b) (A⁻¹)⁺ = (A⁺)⁻¹,

5.2.1.2 Relationships between geometric and kinematic quantities under a SRBM

In addition to preserving the distance between a pair of particles (refer to Problem 5.1), it can be shown that the transformation (5.4a) also preserves the angle θ between any two nonzero vectors, so

$cos θ^{+} = cos θ;$

(5.8)

refer to Problem 5.2. Now consider a surface in the present configuration that contains two points x and y, and has outward unit normal n. Since the SRBM (5.4a) is angle preserving, the angle between n and x − y is the same as the angle between n⁺ and x⁺ − y⁺. As a consequence, it can be shown that

$n^{+} = Qn;$

(5.9)

refer to Problem 5.3. Similarly, it can be shown that the infinitesimal line elements dx⁺ and dx (refer to Section 3.3.1) differ only by a rotation, i.e.,

$d x^{+} = Q d x .$

(5.10)

Problem 5.2

Show that cos θ⁺ = cos θ.

Solution

Consider three different particles: one at reference position X, another at reference position Y, and a third at reference position Z. The motions χ and χ⁺, which differ by a SRBM, map these particles to positions x, y, z at time t, and x⁺, y⁺, z⁺ at time t⁺, respectively. Let θ be the angle between vectors x − y and x − z, and θ⁺ be the angle between vectors x⁺ − y⁺ and x⁺ − z⁺. It follows from definition (2.54) that

$cos θ^{+} = \frac{x^{+} - y^{+}}{| x^{+} - y^{+} |} \cdot \frac{x^{+} - z^{+}}{| x^{+} - z^{+} |} .$

The relations

$x^{+} = Qx + c, y^{+} = Qy + c, z^{+} = Qz + c,$

and the preservation of length under a SRBM, then imply that

$cos θ^{+} = \frac{Q (x - y) \cdot Q (x - z)}{| x - y | | x - z |} .$

si42_e

Orthogonality of Q (refer to definition (2.50)) demands that

$cos θ^{+} = \frac{Q (x - y) \cdot Q (x - z)}{| x - y | | x - z |} = \frac{(x - y) \cdot (x - z)}{| x - y | | x - z |} = cos θ .$

si43_e

Problem 5.3

Prove that n⁺ = Qn.

Solution

Consider a surface in the present configuration that contains two points x and y, and has outward unit normal n. Since the SRBM (5.4a) is angle preserving (refer, for instance, to Problem 5.2), the angle between n and x − y is the same as the angle between n⁺ and x⁺ − y⁺, i.e.,

$\frac{n \cdot (x - y)}{| n | | x - y |} = \frac{n^{+} \cdot (x^{+} - y^{+})}{| n^{+} | | x^{+} - y^{+} |} .$

si44_e

The vectors n and n⁺ are unit vectors, so |n| = |n⁺| = 1. Since SRBMs are length preserving, |x⁺ − y⁺| = |x − y|. Also,

$x^{+} - y^{+} = (Qx + c) - (Qy + c) = Qx - Qy = Q (x - y) .$

These results imply that the original expression simplifies to

$n \cdot (x - y) = n^{+} \cdot Q (x - y),$

$(n - Q^{T} n^{+}) \cdot (x - y) = 0 .$

Since n − Q^Tn⁺ is independent of x − y, we have

$n = Q^{T} n^{+},$

or, premultiplying both sides by Q,

$n^{+} - Qn .$

Recall that many kinematical quantities, such as v, F, C, L, D, and W, are derived from the motion χ. The SRBM χ⁺ will likewise be accompanied by v⁺, F⁺, C⁺, L⁺, D⁺, and W⁺. The transformation (5.4a) imposes relationships between these two sets of quantities. For instance,

$v^{+} = {\dot{x}}^{+} = \dot{\bar{Q (t) x + c (t)}} = \dot{Q} (t) x + Q (t) v + \dot{c} (t) .$

(5.11)

Defining

$Ω (t) = \dot{Q} (t) Q^{T} (t)$

(5.12)

allows us to rewrite (5.11) as

$v^{+} = ΩQx + Qv + \dot{c} .$

(5.13)

It can be shown (refer to Problem 5.4) that the tensor Ω(t) is skew. Another fundamental kinematic relationship is

$F^{+} = \frac{\partial x^{+}}{\partial X} = \frac{\partial x^{+}}{\partial x} \frac{\partial x}{\partial X} = \frac{\partial}{\partial x} [Q (t) x + c (t)] \frac{\partial x}{\partial X} = QF .$

si105_e (5.14)

Using (5.13) and (5.14), we can verify that

$\begin{array}{l} C^{+} = C, B^{+} = Q B Q^{T}, U^{+} = U, V^{+} = Q V Q^{T}, R^{+} = Q R, \\ E^{+} = E, L^{+} = Q L Q^{T} + Ω, D^{+} = Q D Q^{T}, W^{+} = Q W Q^{T} + Ω, \\ J^{+} = J, ρ^{+} = ρ, d a^{+} = d a, d v^{+} = d v, \end{array}$

si106_e (5.15)

where Q(t) is proper orthogonal and Ω(t) is skew; refer to Problems 5.5–5.10.

Problem 5.4

Prove that the tensor $Ω = \dot{Q} Q^{T}$ is skew.

Solution

Since Q is orthogonal,

$Q^{T} Q = I .$

The material derivative of this expression is

$\dot{\bar{Q^{T} Q}} = \dot{I} .$

It follows from (3.22) and (3.23) that

${\dot{Q}}^{T} Q + Q^{T} \dot{Q} = 0 .$

Use of definition (5.12) leads to

$Q^{T} Ω^{T} Q + Q^{T} ΩQ = 0,$

which implies that

$Ω^{T} + Ω = 0,$

$Ω^{T} = - Ω .$

Hence, Ω is skew (refer to definition (2.16)).

Problem 5.5

Prove that C⁺ = C.

Solution

$C^{+} = {(F^{T})}^{+} F^{+} = {(F^{+})}^{T} F^{+} = {(QF)}^{T} QF = F^{T} Q^{T} QF = F^{T} IF = F^{T} F = C .$

Problem 5.6

Prove that U⁺ = U.

Solution

$U^{+} = \sqrt{C^{+}} = \sqrt{C} = U .$

Problem 5.7

Prove that L⁺ = QLQ^T + Ω.

Solution

$L^{+} = \frac{\partial v^{+}}{\partial x^{+}} = \frac{\partial v^{+}}{\partial x} \frac{\partial x}{\partial x^{+}} = \frac{\partial}{\partial x} (ΩQx + Qv + \dot{c}) \frac{\partial x}{\partial x^{+}} = (Ω Q + QL) Q^{T} = Ω + QL Q^{T} .$

si59_e

Alternatively,

$L^{+} = {(\dot{F})}^{+} {(F^{- 1})}^{+} = \dot{\bar{F^{+}}} {(F^{+})}^{- 1} = \dot{\bar{QF}} {(QF)}^{- 1} = (\dot{Q} F + Q \dot{F}) F^{- 1} Q^{- 1} = \dot{Q} F F^{- 1} Q^{- 1} + Q \dot{F} F^{- 1} Q^{- 1} = \dot{Q} Q^{- 1} + QL Q^{- 1} = \dot{Q} Q^{T} + QL Q^{T} = Ω + QL Q^{T} .$

Problem 5.8

Prove that D⁺ = QDQ^T.

Solution

$\begin{array}{l} D^{+} & = \frac{1}{2} [L^{+} + {(L^{T})}^{+}] & (definition {(3.58)}_{1}) \\ = \frac{1}{2} [L^{+} + {(L^{+})}^{T}] & (result {(5.7)}_{1}) \\ = \frac{1}{2} [QL Q^{T} + Ω + {(QL Q^{T} + Ω)}^{T}] & (result {(5.15)}_{7}) \\ = \frac{1}{2} [QL Q^{T} + Ω + {(QL Q^{T})}^{T} + Ω^{T}] & (result {(2.14)}_{1}) \\ = \frac{1}{2} [QL Q^{T} + Ω + Q L^{T} Q^{T} + Ω^{T}] & (results {(2.14)}_{2} and {(2.14)}_{3}) \\ = \frac{1}{2} [QL Q^{T} + Q L^{T} Q^{T}] & (Ω is skew, definition (2.16)) \\ = Q [\frac{1}{2} (L + L^{T})] Q^{T} & (result (2.12)) \\ = QD Q^{T} & (definition {(3.58)}_{1}) . \end{array}$

si61_e

Problem 5.9

Prove that J⁺ = J.

Solution

$J^{+} = det F^{+} = det (QF) = (det Q) (det F) = det F = J .$

Problem 5.10

Prove that da⁺ = da.

Solution

It follows from (3.75) that

$d a^{+} = n^{+} \cdot (d {\overset{1}{x}}^{+} \times d {\overset{2}{x}}^{+}) .$

si63_e

Then, using (2.62), (5.9), and (5.10), we have

$d a^{+} = Qn \cdot (Q d \overset{1}{x} \times Q d \overset{2}{x}) = [\begin{array}{l} Qn & Q d \overset{1}{x} & Q d \overset{2}{x} \end{array}] .$

si64_e

Definition (2.64) and proper orthogonality of Q then imply that

$d a^{+} = (det Q) [\begin{array}{l} n & d \overset{1}{x} & d \overset{2}{x} \end{array}] = [\begin{array}{l} n & d \overset{1}{x} & d \overset{2}{x} \end{array}] = n \cdot (d \overset{1}{x} \times d \overset{2}{x}) = d a .$

si65_e

This result—that the element of area remains unaltered under a SRBM—is consistent with the length-preserving and angle-preserving properties of transformation (5.4a).

Exercises

1. Prove that dx⁺ = Q dx.

2. Prove that B⁺ = QBQ^T.

3. Prove that V⁺ = QVQ^T.

4. Show that R⁺ = QR.

5. Verify that E⁺ = E.

6. Show that W⁺ = QWQ^T + Ω.

7. Verify that ρ⁺ = ρ.

8. Prove that dv⁺ = dv.

5.2.1.3 Relationships between kinetic quantities under a SRBM

Consider now the tractions t and t⁺ associated with the motions χ and χ⁺, respectively, i.e.,

$t = t (x, t, n), t^{+} = t^{+} (x^{+}, t^{+}, n^{+}),$

where

$x^{+} = Qx + c, t^{+} = t + c, n^{+} = Qn .$

It is physical to assume that t is unaltered apart from orientation by a SRBM, i.e.,

(1) the magnitude of t(x, t, n) is equal to the magnitude of t⁺ (x⁺, t⁺, n⁺), and

(2) the angle θ between t(x, t, n) and x − y, for any y, is the same as the angle θ⁺ between t⁺(x⁺, t⁺, n⁺) and x⁺ − y⁺.

In mathematical language, these invariance assumptions become

$| t | = | t^{+} |$

(5.16a)

and

$\frac{t \cdot (x - y)}{| t | | x - y |} = \frac{t^{+} \cdot (x^{+} - y^{+})}{| t^{+} | | x^{+} - y^{+} |} .$

si110_e (5.16b)

It can be shown that as a consequence of (5.16a) and (5.16b),

$t^{+} = Qt,$

(5.17)

which, in turn, implies that

$T^{+} = QT Q^{T};$

(5.18)

refer to Problems 5.11 and 5.12. Also,

$P^{+} = QP, S^{+} = S .$

(5.19)

Problem 5.11

Prove that t⁺ = Qt.

Solution

Recall invariance assumption (5.16b), i.e.,

$\frac{t \cdot (x - y)}{| t | | x - y |} = \frac{t^{+} \cdot (x^{+} - y^{+})}{| t^{+} | | x^{+} - y^{+} |} .$

si66_e

Since the distance between two particles is unaltered by a SRBM,

$| x^{+} - y^{+} | = | x - y | .$

This observation, together with invariance assumption (5.16a), implies that (5.16b) becomes

$t \cdot (x - y) = t^{+} \cdot (x^{+} - y^{+}) .$

Then, use of

$x^{+} - y^{+} = (Qx + c) - (Qy + c) = Qx - Qy = Q (x - y)$

leads us to conclude that

$t \cdot (x - y) = t^{+} \cdot Q (x - y),$

$(t - Q^{T} t^{+}) \cdot (x - y) = 0 .$

Since t − Q^Tt⁺ and x are independent of y, it follows from (2.99)₃ that differentiation of this scalar expression with respect to vector y gives

$Q^{T} t^{+} - t = 0,$

$t^{+} = Qt .$

Problem 5.12

Prove that T⁺ = QTQ^T.

Solution

Recall from Problem 5.11 that t⁺ = Qt. Also recall from Section 4.6 that t = Tn. Together, these results imply that

$T^{+} n^{+} = QTn .$

Use of n⁺ = Qn leads to

$(T^{+} Q - QT) n = 0 .$

Since the coefficient of the unit normal n is independent of n itself, and n is arbitrary, we conclude that the coefficient vanishes:

$T^{+} Q - QT = 0 .$

Thus,

$T^{+} = QT Q^{T} .$

Exercises

1. Show that P⁺ = QP.

2. Verify that S⁺ = S.

5.2.1.4 Invariance requirements

In summary, for the Cauchy stress T to be invariant under all possible SRBMs of the body, any proposed constitutive equation for T must satisfy

$T^{+} = QT Q^{T}$

when

$x^{+} = Qx + c, v^{+} = ΩQx + Qv + \dot{c}, F^{+} = QF, D^{+} = QD Q^{T}, W^{+} = QW Q^{T} + Ω, etc .,$

for all proper orthogonal Q(t), skew Ω(t), and vector functions c(t) and $\dot{c} (t)$ . Collectively, these conditions are referred to as invariance requirements. As will become evident in Chapters 6 and 7, invariance requirements allow us to reduce postulated forms of the constitutive equation for the Cauchy stress T for different materials. Such reductions are welcomed since they allow the characterization of a material from fewer laboratory experiments.

5.2.2 Material symmetry

In addition to angular momentum and invariance requirements, the constitutive equation for the Cauchy stress T generally must satisfy material symmetry conditions. The motion of a body $B$ may be referred to any number of reference configurations (refer to Section 3.1). Let ₀κ and ₁κ be two such reference configurations. Consider a typical particle Y of $B$ located at position ₀X in reference configuration ₀κ, position ₁X in reference configuration ₁κ, and position x in the present configuration at time t (see Figure 5.2). In the notation of Section 3.1,

$\begin{array}{l} {}_{0} X = {}_{0} κ (Y), & x = \bar{χ} (Y, t) = \bar{χ} ({}_{0} κ^{- 1} ({}_{0} X), t) = {}_{0} χ ({}_{0} X, t), \\ {}_{1} X = {}_{1} κ (Y), & x = \bar{χ} (Y, t) = \bar{χ} ({}_{1} κ^{- 1} ({}_{1} X), t) = {}_{1} χ ({}_{1} X, t) . \end{array}$

si119_e

It follows that

${}_{1} X = {}_{1} χ^{- 1} (x, t) =_{1} χ^{- 1} ({}_{0} χ ({}_{0} X, t), t) = {}_{01} χ ({}_{0} X, t) .$

We denote

${}_{0} F = \frac{\partial_{0} χ}{\partial_{0} X}, {}_{1} F = \frac{\partial_{1} χ}{\partial_{1} X}, H = \frac{\partial_{1} X}{\partial_{0} X} .$

si121_e (5.20)

From (5.20) we have

$H = {}_{1} F^{- 1} {}_{0} F or_{1} F = {}_{0} F H^{- 1} .$

f05-02-9780123946003 — Figure 5.2 A motion referred to two reference configurations.

Suppose the constitutive equation for the Cauchy stress T is assumed to depend on the deformation gradient with respect to a specific reference configuration, say, ₀κ. (This assumption is appropriate for an elastic solid, as will soon become apparent in Chapter 6.) Then,

$T = {}_{0} \overset{˘}{T} ({}_{0} F) .$

The choice of reference configuration is arbitrary. Hence, the constitutive equation may just as well be assumed to depend on the deformation gradient with respect to another reference configuration, say, ₁κ:

$T = {}_{1} \overset{˘}{T} ({}_{1} F) .$

Hence, it follows that

${}_{0} \overset{˘}{T} ({}_{0} F) =_{1} \overset{˘}{T} ({}_{0} F H^{- 1}) .$

(5.21)

In general, the constitutive equation for T depends on the choice of reference configuration. For instance, ₀κ may be stress-free, and ₁κ may be stressed. We would not expect the addition of the same amount of stretch to each configuration to illicit the same response. It may happen, however, that the two reference configurations ₀κ and ₁κ are equivalent in the sense that constitutive functions referred to ₀κ are identical to those referred to ₁κ. If ₀κ and ₁κ are equivalent, then it follows from (5.21) that

${}_{0} \overset{˘}{T} ({}_{0} F) =_{0} \overset{˘}{T} ({}_{0} F H^{- 1}),$

(5.22)

and the tensor H is called a symmetry transformation with respect to the reference configuration ₀κ.

Consider now a particular reference configuration κ, and the set of all configurations _iκ, i = 1,2,…, equivalent to κ. Denote by _iH the gradient of the reference map _iκ with respect to the reference map κ. Each of _iH is then a symmetry transformation with respect to the reference configuration κ; see Figure 5.3. The set of all such symmetry transformations forms a group with respect to tensor multiplication, and is called the symmetry group $G$ of the material relative to the reference configuration κ.

f05-03-9780123946003 — Figure 5.3 Equivalent reference configurations.

One of the properties of a material is the amount of symmetry it possesses, which is reflected in its particular symmetry group $G$ for a given κ. Relations such as (5.22) must hold for all H in $G$ . The restrictions thus placed on the constitutive functions can therefore tell us much about the form of these functions. Hence, material symmetry considerations play a role in reducing the functional dependence of the response functions for a particular material.

On physical grounds, it can be argued that if the density of a material is altered, then the material will exhibit different behavior, i.e., the response function will be altered. Therefore, for H to be an element of the symmetry group $G$ , it must be unimodular (i.e., det H = ±1), so density is preserved between the two reference configurations.

The most symmetry a material can possess, relative to a particular reference configuration κ, is $G = μ$ , where μ is the full unimodular group. For such a material, there is no difference in the response from any two configurations having the same density. This has been taken as one definition of a fluid. By this definition, a fluid is a material for which $G = μ$ , i.e., the symmetry group is the full unimodular group.

The least symmetry that a material can possess in a particular reference configuration is $G = {I}$ . In this case the response functions in the reference configuration are different from those in any other reference configuration.

A material is said to be isotropic if there exists a reference configuration, called the undistorted or stress-free configuration, for which the symmetry group $G$ contains the full orthogonal group $O$ . Hence, for the isotropic material, there is a stress-free state in which there is no preferred orientation.

A solid can be defined as a material that has different responses from two reference configurations if the change from one configuration to the other involves a deformation (as opposed to a rigid rotation or translation). Therefore, under this definition, a solid possesses a reference configuration for which the symmetry group $G$ is a subgroup of the full orthogonal group $O$ .

Reviewing our definitions, we have the following:

$\begin{array}{l} fluid (maximal symmetry) : G = μ; \\ isotropic material : O \subseteq G; \\ solid : G \subseteq O . \end{array}$

si138_e

Since all orthogonal tensors are unimodular (i.e., $O \subset μ$ ), we note that fluids are isotropic.

It can be shown that there exists no group $A$ such that $O \subset A \subset μ$ , so $O$ is maximal in μ. This implies that all isotropic materials are either solids ( $G = O$ ) or fluids ( $G = μ$ ). However, not all solids are isotropic, since there are proper subgroups of the full orthogonal group (e.g., ${I} \subset O$ ). Therefore,

$\begin{array}{l} isotropic solid : G = O (for the stress-free configuration); \\ anisotropic solid : G \subset O (for the stress-free configuration) . \end{array}$

Part II: Thermomechanics

In the thermomechanical theory, the mechanical equations of motion are supplemented by the first and second laws of thermodynamics, and an appropriate set of constitutive equations for the thermal and mechanical quantities.

5.3 Fundamental laws, constitutive equations, thermomechanical processes

Recall from Chapter 4 that the field equations and second law inequality in the thermomechanical theory are

$\dot{ρ} + ρ div \dot{x} = 0,$

(5.23)

$div T + ρ b = ρ \overset{..}{x},$

(5.24)

$T = T^{T},$

(5.25)

$ρ \dot{ε} = T \cdot D + ρ r - div q,$

(5.26)

$- ρ \dot{ε} + T \cdot D + ρ Θ \dot{η} - \frac{1}{Θ} q \cdot grad Θ \geq 0 .$

si151_e (5.27)

Equations (5.23)–(5.26) are the local Eulerian forms of conservation of mass, conservation of linear momentum, conservation of angular momentum, and the first law of thermodynamics (conservation of energy). Inequality (5.27) is the Clausius-Duhem inequality, our particular statement of the second law of thermodynamics. Involved in (5.23)–(5.27) are the quantities

${x, η},$

(5.28)

${T, q, ε, Θ},$

(5.29)

${ρ, b, r} .$

(5.30)

These quantities have been conceptually divided into three sets. This division is not for the purposes of solving initial-value boundary-value problems, but rather for the purposes of placing restrictions on the constitutive equations (or response functions).

The elements of set (5.28) are the independent variables. Other quantities will be determined by constitutive equations that depend on these independent variables. For the purposes of restricting the forms of the constitutive equations, we will be able to specify the motion $\bar{χ} (Y, t)$ and entropy $\bar{η} (Y, t)$ as any function of material particle Y and time t, with the confidence that (5.23), (5.24), and (5.26) can be satisfied.

The elements of set (5.29) are the dependent variables. The stress T, heat flux vector q, internal energy ε, and temperature Θ at a particular particle Y and time t are determined through constitutive equations from $\bar{χ} (Y, τ)$ and $\bar{η} (Y, τ)$ , including time and space derivatives, with τ ≤ t (called the history of χ and η). Therefore, the specification of the motion χ and entropy η throughout the body and time interval of interest also fixes T, q, ε, and Θ.

The elements set of (5.30) are the balancing terms. With χ and η arbitrarily specified and T, q, ε, and Θ determined from χ and η through the response functions, the density ρ, body force b, and heat source r are assigned the values necessary to ensure that (5.23), (5.24), and (5.26) are satisfied. Note that the balancing term ρ depends only on the motion χ, and is independent of the choice of the constitutive functions, whereas the balancing terms b and r can be determined only after the constitutive assumptions have been made.

Therefore, the field equations (5.23)–(5.26) and inequality (5.27) are employed as follows: The conservation laws for mass (5.23), linear momentum (5.24), and energy (5.26) are employed to determine ρ, b, and r. Then, the conservation law for angular momentum (5.25) and the Clausius-Duhem inequality (5.27) place restrictions on the response functions for T, q, ε, and Θ. A group of quantities χ, η, T, q, ε, Θ, ρ, b, and r, each a function of material particle Y and time t, which satisfies the conservation laws (5.23)–(5.26) and Clausius-Duhem inequality (5.27) for all space and time in the domain of interest is called a thermomechanical process.

From the above discussion, we see that we can specify the motion χ and entropy η as functions of space and time arbitrarily and still have them part of a thermomechanical process (i.e., a process that satisfies all the equations and inequality of motion), as long as the constitutive equations for T, q, ε, and Θ satisfy the restrictions imposed by conservation of angular momentum and the Clausius-Duhem inequality, and ρ, b, and r are the functions of space and time demanded by conservation of mass (to determine ρ), conservation of linear momentum (to determine b), and conservation of energy (to determine r).

As an example, suppose we specify

$χ (X, t) = X, \hat{η} (X, t) = 10 t,$

(5.31)

for all X, t, so each particle remains at its reference location, and the entropy of each particle increases linearly in time. We can then explicitly calculate

$\dot{x} = \overset{..}{x} = 0, F = I, J = 1, \dot{η} = 10, etc .$

(5.32)

Constitutive equations have been provided for T, q, ε, and Θ, so they are determined as

$\begin{array}{l} T = \tilde{T} (χ, η) = \tilde{T} (X, 10 t), \\ q = \tilde{q} (χ, η) = \tilde{q} (X, 10 t), \\ ε = \tilde{ε} (χ, η) = \tilde{ε} (X, 10 t), \\ Θ = \tilde{Θ} (χ, η) = \tilde{Θ} (X, 10 t) . \end{array}$

With the functions $\tilde{T}$ , $\tilde{q}$ , $\tilde{ε}$ , and $\tilde{Θ}$ so prescribed for all X and t, the derivatives div T, $\dot{ε}$ , div q, and grad Θ appearing in (5.23)–(5.27) are also prescribed. Then from (5.23), (5.24), and (5.26) we can solve for

$\hat{ρ} (X, t) = ρ_{R}, \hat{b} (X, t) = - \frac{1}{ρ_{R}} div T, \hat{r} (X, t) = \frac{div q}{ρ_{R}} + \dot{ε},$

which are now uniquely determined, from conservation of mass, linear momentum, and energy, in terms of the known functions ρ_R, div T, div q, and $\dot{ε}$ . We know that if we could create these density, body force, and heat supply fields, and produce a material characterized by our chosen constitutive equations, we would observe the thermomechanical process with motion x = X and entropy η = 10t.

The conceptual division given in (5.28)–(5.30) is arbitrary, and was chosen on the basis of the form of the Clausius-Duhem inequality (5.27). Its drawback is the choice of entropy η as an independent variable. Any physical understanding that most people have of entropy is as a vague, conceptual measure of “disorder in the universe.” This understanding is then often exceeded when one is asked to propose a constitutive equation, say, for stress T, as a function of entropy.

A much more comfortable choice as an independent variable is absolute temperature Θ rather than entropy η, since the notion of stress depending on temperature (which can easily be measured with a thermometer or thermocouple) is more familiar. To accomplish the change of independent variable from η to Θ, we must replace the dependent variable ε with ψ through the Legendre transformation

$ψ = ε - Θ η,$

(5.33)

where ψ is the Helmholtz free energy and ε is the internal energy. Under the Legendre transformation (5.33), the fundamental laws (5.23)–(5.26) and the Clausius-Duhem inequality (5.27) become

$\dot{ρ} + ρ div \dot{x} = 0,$

(5.23)

$div T + ρ b = ρ \overset{..}{x},$

(5.24)

$T = T^{T},$

(5.25)

$ρ (\dot{ψ} + Θ \dot{η} + \dot{Θ} η) = T \cdot D + ρ r - div q,$

(5.34)

$- ρ \dot{ψ} + T \cdot D - ρ η \dot{Θ} - \frac{1}{Θ} q \cdot grad Θ \geq 0 .$

(5.35)

The independent variables, dependent variables, and balancing terms are then, as an alternative to (5.28)–(5.30),

${x, Θ},$

(5.36)

${T, q, ψ, η},$

(5.37)

${ρ, b, r} .$

(5.38)

The conservation laws for mass (5.23), linear momentum (5.24), and energy (5.26) or (5.34) hold for all thermomechanical materials. To complete the continuum model for a particular material or class of materials, we must

• postulate constitutive relations for T, q, ε, and Θ at point Y and time t, in terms of $\bar{χ} (Y, τ)$ and $\bar{η} (Y, τ)$ and their space and time derivatives, for τ ≤ t, or

• postulate constitutive relations for T, q, ψ, and η in terms of $\bar{χ} (Y, τ)$ and $\bar{η} (Y, τ)$ and their space and time derivatives, for τ ≤ t.

Either way, the specific choice of constitutive equations characterizes the material for all motion and entropy histories in the first case, or all motion and temperature histories in the second case.

Exercises

1. Show that use of the Legendre transformation (5.33) in inequality (5.27) leads to inequality (5.35).

5.4 Restrictions on the constitutive equations

In addition to being grounded on physical experiments, the constitutive equations proposed for a specific material or class of materials in the thermomechanical theory must satisfy

(1) conservation of angular momentum (5.25),

(2) invariance requirements under SRBMs (there is more on this in Section 5.4.1),

(3) the Clausius-Duhem inequality (5.27) or (5.35) for all thermomechanical processes, and perhaps

(4) some material symmetry requirements (refer to Section 5.2.2).

5.4.1 Invariance under superposed rigid body motions

In this section, we present invariance relations for the thermal quantities, which supplement the invariance relations developed in Section 5.2.1 for the geometric, kinematic, and kinetic quantities.

5.4.1.1 Relationships between thermal quantities under a SRBM

It is reasonable to assume that the specific internal energy ε, specific heat supply r, heat flux h, specific entropy η, and absolute temperature Θ are unaltered by a SRBM, i.e.,

$ε^{+} = ε, r^{+} = r, h^{+} = h, η^{+} = η, Θ^{+} = Θ .$

(5.39)

As a consequence of these invariance assumptions, we can show that

$g^{+} = Qg, g_{R}^{+} = g_{R}, ψ^{+} = ψ, q^{+} = Qq, q_{R}^{+} = q_{R};$

(5.40)

refer to Problems 5.13–5.15. Recall that g and g_R are the spatial and referential temperature gradients (refer, for instance, to (4.64) and (4.65)), ψ is the Helmholtz free energy (refer, for instance, to (5.33)), and q and q_R are the spatial and referential heat flux vectors (refer, for instance, to (4.31), (4.49)₂, and (4.53)).

Problem 5.13

Prove that g⁺ = Qg.

Solution

From definition (4.64)₁ and use of the chain rule, we have

$g^{+} = grad Θ^{+} = \frac{\partial Θ^{+}}{\partial x^{+}} = {(\frac{\partial x}{\partial x^{+}})}^{T} \frac{\partial Θ^{+}}{\partial x} .$

si78_e

It then follows from (5.6) and (5.39)5 that

$g^{+} = {(Q^{T})}^{T} \frac{\partial Θ}{\partial x} = Qg .$

si79_e

Problem 5.14

Prove that g⁺_R = g_R.

Solution

We have

$g_{R}^{+} = Grad Θ^{+} = \frac{\partial Θ^{+}}{\partial X} = \frac{\partial Θ}{\partial X} = Grad Θ = g_{R} .$

Alternatively,

$g_{R}^{+} = {(F^{T})}^{+} g^{+} = {(F^{+})}^{T} g^{+} = {(QF)}^{T} Qg = F^{T} Q^{T} Qg = F^{T} I g = F^{T} g = g_{R} .$

Problem 5.15

Prove that q⁺ = Qq.

Solution

It follows from the invariance assumption h⁺ = h that

$q^{+} \cdot n^{+} = q \cdot n .$

Use of the result n⁺ = Qn and definition (2.13) of the transpose leads to

$(Q^{T} q^{+} - q) \cdot n = 0 .$

Since Q^Tq⁺ − q is independent of n,

$Q^{T} q^{+} - q = 0,$

$q^{+} = Qq .$

If, in addition, we assume

$b^{+} - {\overset{..}{x}}^{+} = Q (b - \overset{..}{x}), P^{+} = P,$

si184_e (5.41)

it can be shown that our invariance relationships together with the integral form of conservation of energy (4.19) can be used to obtain the integral forms of conservation of mass (4.11a), linear momentum (4.11b), and angular momentum (4.11c). This demonstrates that our invariance assumptions (5.16a), (5.16b), (5.39), and (5.41) are sensible in that they are consistent with the conservation laws.

5.4.1.2 Invariance requirements

In summary, we find that for formulation (5.36)–(5.38), the constitutive equations for the Cauchy stress T, heat flux vector q, Helmholtz free energy ψ, and entropy η must satisfy

$T^{+} = QT Q^{T}, q^{+} = Qq, ψ^{+} = ψ, η^{+} = η$

when

$x^{+} = Qx + c, v^{+} = ΩQx + Qv + \dot{c}, F^{+} = QF, D^{+} = QD Q^{T}, W^{+} = QW Q^{T} + Ω, Θ^{+} = Θ, etc .,$

for all proper orthogonal Q(t), skew Ω(t), and vector functions c(t) and $\dot{c} (t)$ .

Exercises

1. Prove that ψ⁺ = ψ.

2. Verify that q⁺_R = q_R.

3. Show that the invariance relations developed in Sections 5.2.1 and 5.4.1, together with the integral form of conservation of energy (4.19), can be used to obtain the integral forms of conservation of mass (4.11a), conservation of linear momentum (4.11b), and conservation of angular momentum (4.11c). (Hint: Conservation of energy must be invariant under all possible SRBMs, i.e., for any proper orthogonal Q(t), skew Ω(t), and vector functions c(t) and $\dot{c} (t)$ . To derive the conservation laws of mass, linear momentum, and angular momentum, consider invariance of conservation of energy under several particular SRBMs. For instance, to derive conservation of mass and conservation of linear momentum, consider the particular SRBM that has, at time t, Q = I, $Ω = \dot{Ω} = 0$ , $\dot{c} = c_{0} \equiv constant$ , and $\dot{c} = 0$ . Then, to derive conservation of angular momentum, consider the particular SRBM that has, at time t, Q = I, Ω = Ω₀ ≡ constant, $\dot{Ω} = 0$ , and $\dot{c} = \dot{c} = 0$ .)