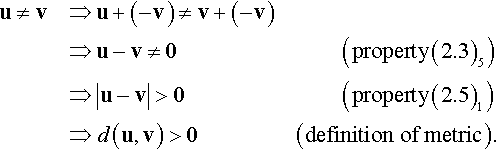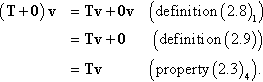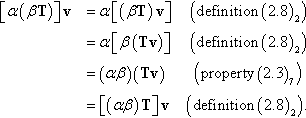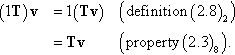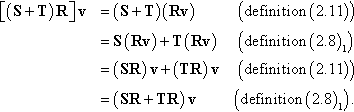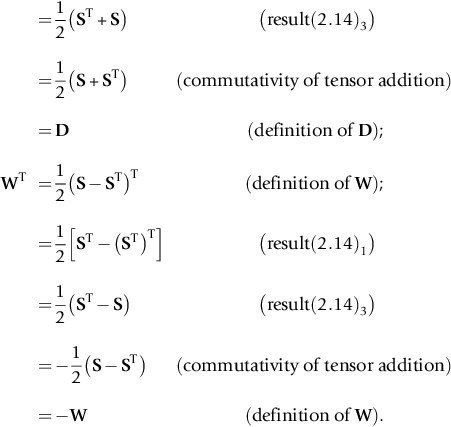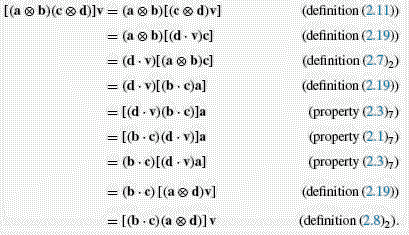2.1.1 Properties of real numbers

Physical quantities such as temperature, pressure, and mass are described by real numbers. For all scalars α, β, γ that are elements of the set of real numbers $\mathbb{R}$ (or, in simplified notation, $\forall \alpha ,\beta ,\gamma \in \mathbb{R}$), the following properties hold:

$\begin{array}{ll}\text{closure of addition,}\hfill & \alpha +\beta \in R;\hfill \\ \text{commutativity of addition,}\hfill & \alpha +\beta =\beta +\alpha ;\hfill \\ \text{associativity of addition,}\hfill & \alpha +\left(\beta +\gamma \right)=\left(\alpha +\beta \right)+\gamma ;\hfill \\ \text{existence of an additive identity,}\hfill & \exists 0\ni \alpha +0=\alpha ;\hfill \\ \text{existence of an additive inverse,}\hfill & \exists \left(-\alpha \right)\ni \alpha +\left(-\alpha \right)=0;\hfill \\ \text{closure of multiplication,}\hfill & \alpha \beta \in R;\hfill \\ \text{commutativity of multiplication,}\hfill & \alpha \beta =\beta \alpha ;\hfill \\ \text{associativity of multiplication,}\hfill & \left(\alpha \beta \right)\gamma =\alpha \left(\beta \gamma \right);\hfill \\ \text{existence of a multiplicative identity,}\hfill & 1\alpha =\alpha ;\hfill \\ \text{existence of a multiplicative inverse}\left(\text{or reciprocal}\right),\hfill & \exists \frac{1}{\alpha }\ni \alpha \frac{1}{\alpha }=1,\alpha \ne 0;\hfill \\ \text{zero product,}\hfill & 0\alpha =0;\hfill \\ \text{distributivity of multiplication over addition,}\hfill & \left(\alpha +\beta \right)\gamma =\alpha \gamma +\beta \gamma .\hfill \end{array}$

Real numbers are an ordered set, so any pair of scalars α and β that are elements of the set of real numbers $\mathbb{R}$ satisfy one and only one of

$\alpha <\beta ,\alpha =\beta ,\alpha >\beta .$

2.1.2 Properties of euclidean space

In this section, we arrive at Euclidean space by progressing from vector spaces, to metric spaces, to normed spaces, and finally to inner product spaces. The vector space (whose elements are called vectors) postulates the algebraic concepts of vector addition, scalar multiplication, and the zero element (or origin) of the space. The metric space (whose elements are called points) postulates topological concepts such as the distance between two points. The normed space (a vector space endowed with a norm) postulates the concept of the length of a vector. Finally, the inner product space (a vector space endowed with an inner product) postulates the concept of an angle between two vectors. Ultimately, we illustrate that every inner product space is also a vector space, a metric space, and a normed space, and is hence endowed with all of their separate properties (refer to Figure 2.3). An n-dimensional inner product space, where n is a positive integer, is known as a Euclidean space ${ℰ}^n$.

Vector space X. The elements of vector space X are called vectors. For all vectors u, v, w in vector space X, and for all scalars α, β that are elements of the set of real numbers $\mathbb{R}$ (or, in simplified notation, ∀ u, v, w ∈ X and $\forall \alpha ,\beta \in \mathbb{R}$), the following properties hold:

$\begin{array}{ll}\text{closure of vector addition,}\hfill & \mathbf{u}+\mathbf{v}\in X;\hfill \\ \text{commutativity of vector addition,}\hfill & \mathbf{u}+\mathbf{v}=\mathbf{v}+\mathbf{u};\hfill \\ \text{associativity of vector addition,}\hfill & \mathbf{u}+\left(\mathbf{v}+\mathbf{w}\right)=\left(\mathbf{u}+\mathbf{v}\right)+\mathbf{w};\hfill \\ \text{existence of an additive identity,}\hfill & \exists \mathbf{0}\ni \mathbf{u}+\mathbf{0}=\mathbf{u};\hfill \\ \text{existence of an additive inverse,}\hfill & \exists \left(-\mathbf{u}\right)\ni \mathbf{u}+\left(-\mathbf{u}\right)=\mathbf{0};\hfill \\ \text{closure of scalar multiplication,}\hfill & \alpha \mathbf{u}\in X;\hfill \\ \text{associativity of scalar multiplication,}\hfill & \alpha \left(\beta \mathbf{u}\right)=\left(\alpha \beta \right)\mathbf{u};\hfill \\ \text{existence of a multiplicative identity,}\hfill & 1\mathbf{u}=\mathbf{u};\hfill \\ \text{distributivity of scalar multiplication over scalar addition,}\hfill & \left(\alpha +\beta \right)\mathbf{u}=\alpha \mathbf{u}+\beta \mathbf{u};\hfill \\ \text{distributivity of scalar multiplication over vector addition,}\hfill & \alpha \left(\mathbf{u}+\mathbf{v}\right)=\alpha \mathbf{u}+\alpha \mathbf{v}.\hfill \end{array}$

For a vector space we have the algebraic concepts of linear combination, independence, dependence, span, linear manifold, basis, and dimension.

Metric space X. The elements of metric space X are called points. The real-valued function d(u, v) is called the metric of X; it accepts points u and v as inputs, and provides the real-valued distance between points u and v as output. The metric d(u, v) is defined such that the following properties hold ∀ u, v, w ∈ X:

$\mathbf{u}\ne \mathbf{v}\Rightarrow d\left(\mathbf{u},\mathbf{v}\right)>0,d\left(\mathbf{u},\mathbf{u}\right)=0,d\left(\mathbf{u},\mathbf{v}\right)=d\left(\mathbf{v},\mathbf{u}\right),d\left(\mathbf{u},\mathbf{w}\right)\le d\left(\mathbf{u},\mathbf{v}\right)+d\left(\mathbf{v},\mathbf{w}\right).$

For a metric space we have the topological concepts of open sets, closed sets, continuity, convergence, completeness, compactness, connectedness, and boundedness. Note that we can have a vector space without the notion of a metric, and a metric space without the notions of scalar multiplication or a zero element (i.e., an origin).

Normed space X. The normed space X is a vector space in which there exists a real-valued function |u| known as the norm of the vector u; the norm accepts vector u as input, and provides the real-valued length of u as output. The norm is defined such that the following properties hold ∀ u, v ∈ X and $\forall \alpha \in \mathbb{R}$:

$\mathbf{u}\ne \mathbf{0}\Rightarrow \left|\mathbf{u}\right|>0,\left|\mathbf{0}\right|=0,\left|\alpha \mathbf{u}\right|=\left|\alpha \right|\left|\mathbf{u}\right|,\left|\mathbf{u}+\mathbf{v}\right|\le \left|\mathbf{u}\right|+\left|\mathbf{v}\right|.$

By definition, every normed space is a vector space (properties (2.5) of a normed space are defined on a vector space). In addition, we can show (refer to Problem 2.1 and Figure 2.3) that every normed space is also a metric space if we define the metric d(u, v) ≡ |u − v|, called the natural metric generated by the norm. Hence, the elements of a normed space can be referred to as either vectors or points. That is, we may think of x as a point in space, or a vector from the zero element (origin) to the point. The length |x| of the vector x is the distance between point x and the origin. The distance d(u, v) between two points u, v is the length |u − v| of the difference u − v of the vectors u, v.

Inner product space X. The inner product space X is a vector space in which there exists a real-valued function u · v known as the inner product of vectors u and v; the inner product accepts vectors u and v as inputs, and provides a real-valued quantity related to the angle between u and v as output. (Look ahead to Eq. (2.54).) The inner product is defined such that the following properties hold ∀ u, v, w ∈ X and $\forall \alpha \in \mathbb{R}$:

$\mathbf{u}·\mathbf{v}=\mathbf{v}·\mathbf{u},\left(\alpha \mathbf{u}\right)·\mathbf{v}=\alpha \left(\mathbf{u}·\mathbf{v}\right),\left(\mathbf{u}+\mathbf{v}\right)·\mathbf{w}=\mathbf{u}·\mathbf{w}+\mathbf{v}·\mathbf{w},\mathbf{u}\ne 0\Rightarrow \mathbf{u}·\mathbf{u}>0.$

By definition, every inner product space is a vector space (properties (2.6) of an inner product space are defined on a vector space). It can be shown (refer to Problem 2.3 and Figure 2.3) that every inner product space is also a normed space and a metric space if |u| = (u · u)^1/2 and d(u, v) = [(u − v) · (u − v)]^1/2. These are called the natural norm and natural metric, respectively, generated by the inner product. An n-dimensional inner product space, where n is a positive integer, is known as a Euclidean space ${ℰ}^n$. We hereafter specialize to three-dimensional Euclidean space ${ℰ}^3$.

All results obtained in this treatise follow rigorously from the postulated properties(2.1)–(2.6).

2.2.1 Second-order tensors, zero tensor, identity tensor

A second-order tensor (or tensor, for short) is defined only by how it acts on an arbitrary vector (a vector is also known as a first-order tensor). In particular, a second-order tensor T is an operation that assigns to each vector v in vector space ${ℰ}^3$ a vector Tv in vector space ${ℰ}^3$ such that

$\mathbf{T}\left(\mathbf{v}+\mathbf{w}\right)=\mathbf{Tv}+\mathbf{Tw},\mathbf{T}\left(\alpha \mathbf{v}\right)=\alpha \left(\mathbf{Tv}\right)$

for any vectors $\mathbf{v},\mathbf{w}\in {ℰ}^3$ and scalars $\alpha \in \mathbb{R}$. Property (2.7)₁ indicates that the map of the sum is the sum of the maps, and property (2.7)₂ indicates that the map of the product is the product of the map; thus, a second-order tensor is a linear map from vector space ${ℰ}^3$ to vector space ${ℰ}^3$. The set of all second-order tensors is denoted by $\mathcal{L}$.

Addition and scalar multiplication of second-order tensors are defined by

$\left(\mathbf{S}+\mathbf{T}\right)\mathbf{v}=\mathbf{Sv}+\mathbf{Tv},\left(\alpha \mathbf{S}\right)\mathbf{v}=\alpha \left(\mathbf{Sv}\right)$

for any tensors $\mathbf{S},\mathbf{T}\in \mathcal{L}$, vectors $\mathbf{v}\in {\epsilon }^3$, and scalars $\alpha \in \mathbb{R}$. Note that the operations S + T and αS are defined by how they act on an arbitrary vector v. With definition (2.7), definition (2.8), and the properties of ${\epsilon }^3$ (refer to Section 2.1.2), it can be shown (refer to Problem 2.4) that all of the requirements (2.3) are satisfied. Hence, the set $\mathcal{L}$ of all second-order tensors is a vector space.

Recall from properties (2.3) that every vector space has a zero element. The zero element of $\mathcal{L}$ is the zero tensor 0 that maps every $\mathbf{v}\in {\epsilon }^3$ to the zero vector 0 of ${\epsilon }^3$, i.e.,

$\mathbf{0}\mathbf{v}=\mathbf{0}.$

The identity tensor I maps every $\mathbf{v}\in {\epsilon }^3$ to itself, i.e.,

$\mathbf{Iv}=\mathbf{v}.$

2.2.2 Product, transpose, symmetry

The product of two tensors is defined by

$\left(\mathbf{ST}\right)\mathbf{v}=\mathbf{S}\left(\mathbf{Tv}\right)$

for any vector $\mathbf{v}\in {\epsilon }^3$. Note that this product is defined such that v is first mapped by T to Tv, then Tv is mapped by S to S(Tv); see Figure 2.4. It can be shown (refer to Problem 2.5) that with definition (2.11) the product of two tensors is itself a tensor. Tensor multiplication is not commutative, since in general ST ≠ TS, although it is associative. It can be verified (refer to Problem 2.6) that tensor multiplication distributes over tensor addition as

$\left(\mathbf{S}+\mathbf{T}\right)\mathbf{R}=\mathbf{SR}+\mathbf{TR}.$

The transpose S^T of S is defined by

$\mathbf{Su}·\mathbf{v}=\mathbf{u}·{\mathbf{S}}^{\text{T}}\mathbf{v}$

for any vectors $\mathbf{u},\mathbf{v}\in {\epsilon }^3$. It can be shown (refer to Problem 2.7) that the transpose is unique. We have, for instance (refer to Problems 2.8–2.11),

${\left(\mathbf{S}+\mathbf{T}\right)}^{\text{T}}={\mathbf{S}}^{\text{T}}+{\mathbf{T}}^{\text{T}},{\left(\mathbf{SR}\right)}^{\text{T}}={\mathbf{R}}^{\text{T}}{\mathbf{S}}^{\text{T}},{\left({\mathbf{S}}^{\text{T}}\right)}^{\text{T}}=\mathbf{S},{\mathbf{I}}^{\text{T}}=\mathbf{I}.$

A tensor for which

${\mathbf{S}}^{\text{T}}=\mathbf{S}$

is called a symmetric tensor, and a tensor for which

${\mathbf{S}}^{\text{T}}=-\mathbf{S}$

is called a skew tensor. It can be shown (refer to Problem 2.12) that every tensor S can be additively decomposed into a symmetric part D and a skew part W, i.e.,

$\mathbf{S}=\mathbf{D}+\mathbf{W},$

where

$\mathbf{D}=\frac{1}{2}\left(\mathbf{S}+{\mathbf{S}}^{\text{T}}\right),\mathbf{W}=\frac{1}{2}\left(\mathbf{S}-{\mathbf{S}}^{\text{T}}\right).$

2.2.3 Dyadic product

The dyadic product (or tensor product) a ⊗ b accepts two vectors $\mathbf{a},\mathbf{b}\in {\epsilon }^3$ as inputs and provides as output a second-order tensor that maps each $\mathbf{v}\in {\epsilon }^3$ to the vector (b · v)a. That is,

$(\mathbf{a}\otimes \mathbf{b})\mathbf{v}=(\mathbf{b}·\mathbf{v})\mathbf{a},$

where (b · v)a is the projection of b onto v in the direction of a. We have, for instance (refer to Problems 2.14–2.17),

${(\mathbf{a}\otimes \mathbf{b})}^{\text{T}}=\mathbf{b}\otimes \mathbf{a},\mathbf{S}(\mathbf{a}\otimes \mathbf{b})=(\mathbf{Sa})\otimes \mathbf{b},(\mathbf{a}\otimes \mathbf{b})\mathbf{S}=\mathbf{a}\otimes ({\mathbf{S}}^{\mathbf{T}}\mathbf{b}),(\mathbf{a}\otimes \mathbf{b})(\mathbf{c}\otimes \mathbf{d})=(\mathbf{b}·\mathbf{c})(\mathbf{a}\otimes \mathbf{d}).$