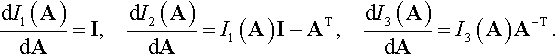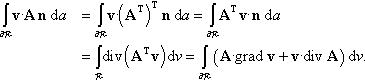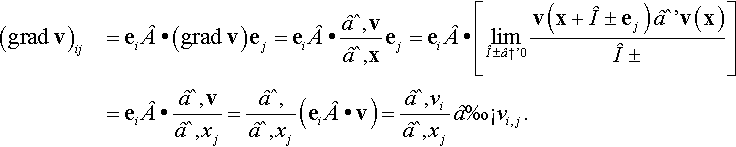2.3 Eigenvalues, eigenvectors, polar decomposition, invariants

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

2.2.7 Vector product, scalar triple product

The angle θ between two vectors u and v in $ε^{3}$ is defined by

$cos θ = \frac{u \cdot v}{| u | | v |},$

(2.54)

where |u| is the natural norm, i.e., |u| = (u · u)^1/2. Then the vector product in $ε^{3}$ is defined by

$u \times v = | u | | v | n sin θ, | n | = 1, u \cdot n = v \cdot n = 0 .$

(2.55)

As such, the vector product accepts two vectors u and v as inputs, and provides a single vector in the direction of n as output. Note that n is the unit normal to the plane containing u and v; thus, two vector products are possible in $ε^{3}$ . We single out the one for which {u, v, n} form a right-handed set. We also demand that the basis {e₁, e₂, e₃} is right-handed, so

$e_{1} \times e_{2} = e_{3}, e_{2} \times e_{3} = e_{1}, e_{3} \times e_{1} = e_{2}, e_{1} \times e_{3} = - e_{2}, e_{2} \times e_{1} = - e_{3}, e_{3} \times e_{2} = - e_{1}, e_{1} \times e_{1} = 0, e_{2} \times e_{2} = 0, e_{3} \times e_{3} = 0 .$

(2.56)

Using indicial notation, we can write the nine equations in (2.56) as the single expression

$e_{i} \times e_{j} = ε_{ijk} e_{k},$

(2.57)

where ε_ijk is the permutation symbol, defined such that

$ε_{ijk} = {\begin{array}{l} 1 & if ijk = 123 = 231 = 312, \\ - 1 & if ijk = 132 = 213 = 321, \\ 0 & otherwise . \end{array}$

si373_e (2.58)

Then, it can be shown (refer to Problem 2.41) that

$u \times v = ε_{ijk} u_{i} v_{j} e_{k},$

(2.59)

i.e.,

$u \times v = (u_{2} v_{3} - u_{3} v_{2}) e_{1} + (u_{3} v_{1} - u_{1} v_{3}) e_{2} + (u_{1} v_{2} - u_{2} v_{1}) e_{3} = | \begin{array}{l} e_{1} & e_{2} & e_{3} \\ u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \end{array} | .$

si375_e (2.60)

Note that the vector product is anticommutative, i.e.,

$u \times v = - v \times u .$

(2.61)

Problem 2.41

Show that u × v = ε_ijk u_i v_je_k.

Solution

$u \times v = u_{i} e_{i} \times v_{j} e_{j} = u_{i} v_{j} (e_{i} \times e_{j}) = ε_{ijk} u_{i} v_{j} e_{k} .$

The scalar triple product [u v w] of three vectors is defined by

$[u v w] = u \cdot (v \times w) .$

(2.62)

It can be shown that

$[u v w] = [v w u] = [w u v] .$

(2.63)

The absolute value of [u v w] is the volume of the parallelepiped determined by u, v, and w. Also,

$det S = \frac{[Su Sv Sw]}{[u v w]} .$

si379_e (2.64)

Corresponding to each skew tensor $W \in L$ is an axial vector $w \in ε^{3}$ , i.e.,

$Wv = w \times v$

(2.65)

for any $v \in ε^{3}$ . Because of this correspondence, the set of all skew tensors is a three-dimensional inner product space $ε^{3}$ (refer to Problem 2.42).

Problem 2.42

Verify in Cartesian component notation that the set of all symmetric tensors is a six-dimensional inner product space $ε^{6}$ , and the set of all skew tensors is a three-dimensional inner product space $ε^{3}$ .

Solution

Consider an arbitrary symmetric tensor D. The Cartesian component form of D is

$D = D_{ij} e_{i} \otimes e_{j} = D_{11} e_{1} \otimes e_{1} + D_{12} e_{1} \otimes e_{2} + D_{13} e_{1} \otimes e_{3} + D_{21} e_{2} \otimes e_{1} + D_{22} e_{2} \otimes e_{2} + D_{23} e_{2} \otimes e_{3} + D_{31} e_{3} \otimes e_{1} + D_{32} e_{3} \otimes e_{2} + D_{33} e_{3} \otimes e_{3} .$

But, since D is symmetric (i.e., D^T = D),

$D_{ij} = e_{i} \cdot D e_{j} = D e_{j} \cdot e_{i} = e_{j} \cdot D^{T} e_{i} = e_{j} \cdot D e_{i} = D_{ji},$

$D_{12} = D_{21}, D_{13} = D_{31}, D_{23} = D_{32} .$

Thus,

$D = D_{11} e_{1} \otimes e_{1} + D_{12} (e_{1} \otimes e_{2} + e_{2} \otimes e_{1}) + D_{13} (e_{1} \otimes e_{3} + e_{3} \otimes e_{1}) + D_{22} e_{2} \otimes e_{2} + D_{23} (e_{2} \otimes e_{3} + e_{3} \otimes e_{2}) + D_{33} e_{3} \otimes e_{3} .$

It follows that the basis of any symmetric tensor D has six elements, so the set of all symmetric tensors is a six-dimensional inner product space $ε^{6}$ . Note that only six components (D₁₁, D₁₂, D₁₃, D₂₂, D₂₃, D₃₃) are required to fully specify D.

Similarly, since W is skew (i.e., W^T = −W),

$W_{ij} = e_{i} \cdot W e_{j} = W e_{j} \cdot e_{i} = e_{j} \cdot W^{T} e_{i} = - e_{j} \cdot W e_{i} = - W_{ji},$

$W_{11} = W_{22} = W_{33} = 0, W_{12} = - W_{21}, W_{13} = - W_{31}, W_{23} = - W_{32} .$

Thus,

$W = W_{12} (e_{1} \otimes e_{2} - e_{2} \otimes e_{1}) + W_{13} (e_{1} \otimes e_{3} - e_{3} \otimes e_{1}) + W_{23} (e_{2} \otimes e_{3} - e_{3} \otimes e_{2}) .$

It follows that the basis of any skew tensor W has three elements, so the set of all skew tensors is a three-dimensional inner product space $ε^{3}$ . Note that only three components (W₁₂, W₁₃, W₂₃) are required to fully specify W.

2.3 Eigenvalues, eigenvectors, polar decomposition, invariants

The presentation of the conceptual material in this section again follows [2]. In general, a tensor S maps a vector u to a vector Su. The vector Su typically has a length and orientation different from those of u. However, for special unit vectors a called eigenvectors, the tensor S maps a to a vector Sa that is parallel to a, i.e.,

$Sa = α a .$

(2.66)

The scalar α is referred to as an eigenvalue of S corresponding to the eigenvector a.

It can be shown that if S is positive definite, then its eigenvalues are strictly positive (refer to Problem 2.43). Further, if S is both symmetric and positive definite, then it can be shown that det S > 0, so S⁻¹ exists (refer to Problem 2.44).

Problem 2.43

Prove that the eigenvalues of a positive-definite tensor are strictly positive.

Solution

Recall from (2.53) that if the tensor P is positive definite, then v · Pv > 0 for any vector v ≠ 0. Suppose, then, that we choose v = a, where a is any eigenvector of P. Then

$a \cdot Pa > 0 .$

But, by (2.66), we have Pa = αa, where α is the eigenvalue corresponding to a, which implies that

$α (a \cdot a) > 0 .$

Since eigenvectors are of unit length (a · a = |a|² = 1), it follows that α > 0, i.e., the eigenvalue α corresponding to any eigenvector a of tensor P is positive.

Problem 2.44

Prove that if the tensor P is symmetric and positive definite, then det P > 0, so its inverse P⁻¹ exists.

Solution

If P is a symmetric tensor, then by (2.67a) we have

$P = α_{1} a_{1} \otimes a_{1} + α_{2} a_{2} \otimes a_{2} + α_{3} a_{3} \otimes a_{3},$

where a₁, a₂, a₃ are the eigenvectors of P, and α₁, α₂, α₃ are the corresponding eigenvalues of P. Hence, by (2.46),

$det P = det [P] = det [\begin{array}{l} α_{1} & 0 & 0 \\ 0 & α_{2} & 0 \\ 0 & 0 & α_{3} \end{array}] = α_{1} α_{2} α_{3} .$

si203_e

Recall from Problem 2.43 that if a tensor P is positive definite, then its eigenvalues α₁, α₂, and α₃ are all positive. Hence, det P = α₁α₂α₃ > 0, and P is invertible.

If S is symmetric, its eigenvectors {a₁, a₂, a₃} constitute an orthonormal basis for $ε^{3}$ (the corresponding eigenvalues are α₁, α₂, and α₃). Additionally, any symmetric S in $L$ can be written with respect to a basis of its eigenvectors {a_i ⊗ a_j} as

$S = α_{1} a_{1} \otimes a_{1} + α_{2} a_{2} \otimes a_{2} + α_{3} a_{3} \otimes a_{3} = \sum_{i = 1} α_{i} a_{i} \otimes a_{i},$

(2.67a)

or, in matrix form,

$[S] = [\begin{matrix} α_{1} & 0 & 0 \\ 0 & α_{2} & 0 \\ 0 & 0 & α_{3} \end{matrix}] .$

si389_e (2.67b)

If B is a symmetric, positive-definite tensor, then there exists a unique symmetric, positive-definite tensor V such that

$V^{2} \equiv VV = B .$

(2.68)

That is, $V = \sqrt{B}$ .

If F is an invertible tensor (det F ≠ 0), then

$F = RU = VR,$

(2.69)

where U and V are symmetric, positive-definite tensors, and R is an orthogonal tensor. The multiplicative decomposition (2.69) is referred to as the polar decomposition of F. The tensors U, V, and R are unique, with

$U = \sqrt{F^{T} F}, V = \sqrt{F F^{T}}, R = F U^{- 1} .$

(2.70)

The terms in (2.70) make sense, because F^TF and FF^T can be shown to be symmetric and positive definite (refer to Problem 2.45), so we may use (2.68); also, det F ≠ 0 implies that det U ≠ 0, so U⁻¹ exists. Note that if det F > 0, then R is proper orthogonal.

Problem 2.45

Prove that if F is nonsingular, then F^TF and F F^T are symmetric and positive definite.

Solution

First, we verify that F^TF and F F^T are symmetric. We have

${(F^{T} F)}^{T} = F^{T} {(F^{T})}^{T} = F^{T} F, {(F F^{T})}^{T} = {(F^{T})}^{T} F^{T} = F F^{T} .$

Thus, according to definition (2.15), F^TF and F F^T are symmetric.

Next, we verify that F^TF is positive definite. We have

$v \cdot (F^{T} F) v = v \cdot F^{T} (Fv) = Fv \cdot Fv .$

According to property (2.6)₄ of inner product spaces, if Fv ≠ 0, then Fv · Fv > 0. Since F is nonsingular, det F ≠ 0, i.e., Fv = 0 if and only if v = 0. Hence, it follows that

$v \cdot (F^{T} F) v > 0$

for any vector v ≠ 0, so, according to definition (2.53), F^TF is positive definite.

Lastly, we verify that F F^T is positive definite. We use result (2.47)₂ to argue that det F^T = det F ≠ 0 (i.e., if F is nonsingular, then so is F^T), so F^Tv = 0 if and only if v = 0, which implies

$v \cdot (F F^{T}) v = v \cdot F (F^{T} v) = F^{T} v \cdot F^{T} v > 0$

for any vector v ≠ 0. Thus, according to definition (2.53), F F^T is positive definite.

A nontrivial solution of the eigenvalue problem (2.66) requires

$det (S - α I) = 0 .$

(2.71)

It can be shown that

$det (S - α I) = - α^{3} + α^{3} I_{1} (S) - α I_{2} (S) + I_{3} (S),$

(2.72)

so (2.71) becomes

$- α^{3} + α^{2} I_{1} (S) - α I_{2} (S) + I_{3} (S) = 0,$

(2.73)

where

$I_{1} (S) = tr S, I_{2} (S) = \frac{1}{2} [{(tr S)}^{2} - tr (S^{2})], I_{3} (S) = det S$

si397_e (2.74)

are called the principal invariants of S. Equation (2.73) is called the characteristic equation of S. According to the Cayley-Hamilton theorem, every tensor S satisfies its own characteristic equation, i.e.,

$- S^{3} + S^{2} I_{1} (S) - S I_{2} (S) + I I_{3} (S) = 0 .$

(2.75)

Note that if S is symmetric, then it follows from (2.67b) and (2.74) that

$I_{1} (S) = α_{1} + α_{2} + α_{3}, I_{2} (S) = α_{1} α_{2} + α_{2} α_{3} + α_{1} α_{3}, I_{3} (S) = α_{1} α_{2} α_{3} .$

(2.76)

Thus, two symmetric tensors with the same eigenvalues have the same principal invariants.

2.4 Tensors of order three and four

We call linear transformations from $ε^{3}$ to $L$ , or from $L$ to $ε^{3}$ , third-order tensors. Thus, a third-order tensor D⁽³⁾ is a linear map that assigns to each vector $u \in ε^{3}$ a second-order tensor $D^{(3)} u \in L$ such that

$D^{(3)} (u + v) = D^{(3)} u + D^{(3)} v, D^{(3)} (α v) = α (D^{(3)} v),$

(2.77)

or a linear map that assigns to each second-order tensor $T \in L$ a vector $D^{(3)} T \in ε^{3}$ such that

$D^{(3)} (S + T) = D^{(3)} S + D^{(3)} T, D^{(3)} (α T) = α (D^{(3)} T)$

(2.78)

for any second-order tensors $S, T \in L$ , vectors $u, v \in ε^{3}$ , and scalars $α \in R$ . The set of all third-order tensors is denoted by $L^{(3)}$ .

If a, b, and c are vectors in $ε^{3}$ , we define the third-order tensor a ⊗ b ⊗ c by

$(a \otimes b \otimes c) v = a \otimes b (c \cdot v), (a \otimes b \otimes c) v \otimes w = a (c \cdot v) (b \cdot w)$

(2.79)

for any vectors $v, w \in ε^{3}$ .

The Cartesian components D_ijk of a third-order tensor D⁽³⁾ are defined by

$D_{ijk} = (e_{i} \otimes e_{j}) \cdot (D^{(3)} e_{k}),$

(2.80)

and we have

$D^{(3)} = D_{ijk} e_{i} \otimes e_{j} \otimes e_{k} .$

(2.81)

e_i ⊗ e_j ⊗ e_k is a basis for $L^{(3)} = ε^{27}$ , a 27-dimensional inner product space.

We call linear transformations from $ε^{3}$ to $L^{(3)}$ , $L$ to $L$ , or $L^{(3)}$ to $ε^{3}$ fourth-order tensors. Thus, a fourth-order tensor C⁽⁴⁾ is a linear map that assigns to each vector $u \in ε^{3}$ a third-order tensor

$D^{(3)} = C^{(4)} u,$

(2.82)

or to each second-order tensor $T \in L$ a second-order tensor

$S = C^{(4)} T,$

(2.83)

or to each third-order tensor $ε^{(3)} \in L^{(3)}$ a vector

$v = C^{(4)} ε^{(3)} .$

(2.84)

The set of all fourth-order tensors is denoted by $L^{(4)}$ .

If a, b, c, and d are vectors in $ε^{3}$ , we define the fourth-order tensor a ⊗ b ⊗ c ⊗ d by

$\begin{array}{l} (a \otimes b \otimes c \otimes d) v = a \otimes b \otimes c (d \cdot v), \\ (a \otimes b \otimes c \otimes d) v \otimes w = a \otimes b (d \cdot v) (c \cdot w), \\ (a \otimes b \otimes c \otimes d) v \otimes w \otimes z = a (d \cdot v) (c \cdot w) (b \cdot z) \end{array}$

si434_e

for any vectors $v, w, z \in ε^{3}$ .

The Cartesian components C_ijkl of C⁽⁴⁾ are defined by

$C_{ijkl} = (e_{i} \otimes e_{j}) \cdot (C^{(4)} e_{k} \otimes e_{l}),$

(2.86)

and we have

$C^{(4)} = C_{ijkl} e_{i} \otimes e_{j} \otimes e_{k} \otimes e_{l} .$

(2.87)

e_i ⊗ e_j ⊗ e_k ⊗ e_l is a basis for $L^{(4)} = ε^{81}$ , an 81-dimensional inner product space.

2.5 Tensor calculus

2.5.1 Partial derivatives

Let φ be a scalar-valued function of a tensor T, vector x, and scalar t, i.e.,

$φ = φ (T, x, t) .$

(2.88)

We define the partial derivatives of φ by

$\begin{array}{l} \frac{\partial}{\partial t} φ (T, x, t) = lim_{α \to 0} \frac{1}{α} [φ (T, x, t + α) - φ (T, x, t)], \\ [\frac{\partial}{\partial x} φ (T, x, t)] \cdot u = lim_{α \to 0} \frac{1}{α} [φ (T, x, t + α u, t) - φ (T, x, t)], \\ [\frac{\partial}{\partial T} φ (T, x, t)] \cdot S = lim_{α \to 0} \frac{1}{α} [φ (T + α S, x, t) - φ (T, x, t)] \end{array}$

si440_e (2.89)

for all vectors u in $ε^{3}$ and all tensors S in $L$ . Note that α is a real number. Also note that ∂φ/∂t is a scalar, ∂φ/∂x is a vector, and ∂φ/∂T is a tensor.

Let v be a vector-valued function of tensor T, vector x, and scalar t, i.e.,

$v = v (T, x, t) .$

(2.90)

We define the partial derivatives of v by

$\begin{array}{l} \frac{\partial}{\partial t} v (T, x, t) = lim_{α \to 0} \frac{1}{α} [v (T, x, t + α) - v (T, x, t)], \\ [\frac{\partial}{\partial x} v (T, x, t)] u = lim_{α \to 0} \frac{1}{α} [v (T, x, t + α u, t) - v (T, x, t)], \\ [\frac{\partial}{\partial T} v (T, x, t)] S = lim_{α \to 0} \frac{1}{α} [v (T + α S, x, t) - v (T, x, t)], \end{array}$

si444_e (2.91)

for all vectors u in $ε^{3}$ and all tensors S in $L$ . Note that ∂v/∂t is a vector and ∂v/∂x is a tensor. The quantity ∂v/∂T maps a tensor S to a vector, and is called a third-order tensor (refer to Section 2.4).

Let A be a tensor-valued function of tensor T, vector x, and scalar t, i.e.,

$A = A (T, x, t) .$

(2.92)

The partial derivatives of A are defined by

$\begin{array}{l} \frac{\partial}{\partial t} A (T, x, t) = lim_{α \to 0} \frac{1}{α} [A (T, x, t + α) - A (T, x, t)], \\ [\frac{\partial}{\partial x} A (T, x, t)] u = lim_{α \to 0} \frac{1}{α} [A (T, x + α u, t) - A (T, x, t)], \\ [\frac{\partial}{\partial T} A (T, x, t)] S = lim_{α \to 0} \frac{1}{α} [A (T + α S, x, t) - A (T, x, t)], \end{array}$

si448_e (2.93)

for all vectors u in $ε^{3}$ and all tensors S in $L$ . Note that ∂A/∂t is a tensor. The quantity ∂A/∂x is a third-order tensor, i.e., it maps vectors to tensors; the fourth-order tensor ∂A/∂T maps tensors to tensors (refer to Section 2.4).

Recall from Section 2.3 that the principal invariants of a tensor A are

$I_{1} (A) = tr A, I_{2} (A) = \frac{1}{2} [{(tr A)}^{2} - tr (A^{2})], I_{3} (A) = det A .$

It can be shown that (refer to Problems 2.46–2.48)

$\frac{d I_{1} (A)}{d A} = I, \frac{d I_{2} (A)}{d A} = I_{1} (A) I - A^{T}, \frac{d I_{3} (A)}{d A} = I_{3} (A) A^{- T} .$

si452_e (2.94)

Problem 2.46

Prove in direct notation that $\frac{d I_{1} (A)}{d A} = I$ si208_e .

Solution

Using the definition (2.89)₃ of the derivative of a scalar with respect to a tensor, and the properties of the trace, we have, for all tensors S in $L$ ,

Since S is arbitrary, it follows that $\frac{d I_{1} (A)}{d A} = I$ si211_e .

Problem 2.47

Prove in direct notation that $\frac{d I_{2} (A)}{d A} = I_{1} (A) I - A^{T}$ .

Solution

Note that in what follows, we employ the notation AA ≡ A², as is done elsewhere in this book. Using the definition (2.89)₃ of the derivative of a scalar with respect to a tensor, and the properties of the trace, we have, for all tensors S in $L$ ,

Recall from Problem 2.46 that

$tr S = tr (SI) = tr (S I^{T}) = S \cdot I = I \cdot S .$

Thus, it follows that

$\frac{d I_{2} (A)}{d A} \cdot S = (I_{1} (A) I - A^{T}) \cdot S .$

si216_e

Since S is arbitrary, $\frac{d I_{2} (A)}{d A} = I_{1} (A) I - A^{T}$ si217_e .

Problem 2.48

Prove in direct notation that $\frac{d I_{3} (A)}{d A} = I_{3} (A) A^{- T}$ .

Solution

In this problem, we will make use of the result

$det (U + I) = 1 + tr U + \frac{1}{2} [{(tr U)}^{2} - tr U^{2}] + det U = det (I + U),$

which holds for any tensor U in $L$ and follows from (2.72) with α = −1. Note that I₃(A) = det A, and det A is a scalar. Using the definition (2.89)₃ of the derivative of a scalar with respect to a tensor, we have, for all tensors S in $L$ ,

Since S is arbitrary and I₃(A) = det A, it follows that $\frac{d I_{3} (A)}{d A} = I_{3} (A) A^{- T}$ .

2.5.2 Chain rule, gradient, divergence, curl, divergence theorem

If T and x in (2.88), (2.90), and (2.92) also depend on t, then the chain rule implies that

$\begin{array}{l} \frac{d}{d t} φ (T (t), x (t), t) & = \frac{\partial φ}{\partial T} \cdot \frac{d T}{d t} + \frac{\partial φ}{\partial x} \cdot \frac{d x}{d t} + \frac{\partial φ}{\partial t}, \\ \frac{d}{d t} v (T (t), x (t), t) & = \frac{\partial v}{\partial T} \frac{d T}{d t} + \frac{\partial v}{\partial x} \frac{d x}{d t} + \frac{\partial v}{\partial t}, \\ \frac{d}{d t} A (T (t), x (t), t) & = \frac{\partial A}{\partial T} \frac{d T}{d t} + \frac{\partial A}{\partial x} \frac{d x}{d t} + \frac{\partial A}{\partial t} . \end{array}$

si453_e (2.95)

If the vector x in (2.88), (2.90), and (2.92) is a position vector, we define gradients of the scalar-valued function φ, vector-valued function v, and tensor-valued function A by

$grad φ = \frac{\partial}{\partial x} φ (T, x, t), grad v = \frac{\partial}{\partial x} v (T, x, t), grad A = \frac{\partial}{\partial x} A (T, x, t) .$

si454_e (2.96)

Note that the gradients of scalars, vectors, and tensors are vectors, tensors, and third-order tensors, respectively.

The divergence of a vector-valued function v of position is defined

$div v = tr (grad v),$

(2.97)

which is a scalar. The divergence of a tensor-valued function A of position is defined through

$(div A) \cdot a = div (A^{T} a)$

(2.98)

for any vector a. The divergence of a tensor is a vector. It can be shown (refer to Problems 2.49–2.51) that

$\begin{array}{l} grad (φ v) = φ grad v + v \otimes grad φ, \\ div (φ v) = φ div v + v \cdot grad φ, \\ grad (v \cdot w) = {(grad v)}^{T} w + {(grad w)}^{T} v, \\ div (A^{T} v) = A \cdot grad v + v \cdot div A, \\ grad (\frac{1}{φ}) = - \frac{1}{φ^{2}} grad φ, \\ div (φ A) = φ div A + A grad φ, \\ div (v \otimes w) = v div w + (grad v) w . \end{array}$

si457_e (2.99)

Problem 2.49

Prove in direct notation that grad (φv) = φ grad v + v ⊗ grad φ.

Solution

Note that φv is a vector. Definition (2.96)₂ of the gradient of a vector and definition (2.91)₂ of the partial derivative of a vector with respect to a vector imply that

$[grad (φ v)] u = \frac{\partial (φ v)}{\partial x} u = lim_{α \to 0} \frac{φ (x + α u) v (x + α u) - φ (x) v (x)}{α} .$

Then adding and subtracting φ(x + αu) v(x) to and from the numerator, we have

$\begin{array}{l} [grad (φ v)] u = lim_{α \to 0} \frac{1}{α} [φ (x + α u) v (x + α u) - φ (x + α u) v (x) + φ (x + α u) v (x) - φ (x) v (x)] \\ = lim_{α \to 0} {φ (x + α u) [\frac{v (x + α u) - v (x)}{α}]} + lim_{α \to 0} {[\frac{φ (x + α u) - φ (x)}{α}] v (x)} \\ = [lim_{α \to 0} φ (x + α u)] {lim_{α \to 0} \frac{v (x + α u) - v (x)}{α}} + {lim_{α \to 0} \frac{φ (x + α u) - φ (x)}{α}} v (x) \\ = φ (x) (\frac{\partial v}{\partial x} u) + (\frac{\partial φ}{\partial x} \cdot u) v (x) \\ = (φ grad v) u + (v \otimes grad φ) u \\ = (φ grad v + v \otimes grad φ) u . \end{array}$

si225_e

Since u is arbitrary, it follows that grad (φv) = φ grad v + v ⊗ grad φ.

Problem 2.50

Prove in direct notation that div (φv) = φ div v + v · grad φ.

Solution

Again, note that φv is a vector. Using the definition (2.97) of the divergence of a vector, the result grad (φv) = φ grad v + v ⊗ grad φ from Problem 2.49, and the properties (2.38) of the trace, we have

$div (φ v) = tr [grad (φ v)] = tr (φ grad v + v \otimes grad φ) = tr (φ grad v) + tr (v \otimes grad φ) = φ tr (grad v) + v \cdot grad φ = φ div v + v \cdot grad φ .$

Problem 2.51

Prove in direct notation that grad (v · w) = (grad v)^Tw + (grad w)^Tv.

Solution

Definition (2.96)₁ of the gradient of a scalar and definition (2.89)₂ of the partial derivative of a scalar with respect to a vector imply that

$\begin{array}{l} [grad (v \cdot w)] \cdot u = \frac{\partial (v \cdot w)}{\partial x} \cdot u \\ = lim_{α \to 0} \frac{v (x + α u) \cdot w (x + α u) - v (x) \cdot w (x)}{α} \\ = lim_{α \to 0} \frac{1}{α} [v (x + α u) \cdot w (x + α u) - v (x) \cdot w (x + α u) + v (x) \cdot w (x + α u) - v (x) \cdot w (x)] \\ = lim_{α \to 0} {[\frac{v (x + α u) - v (x)}{α}] \cdot w (x + α u)} + lim_{α \to 0} {v (x) \cdot [\frac{w (x + α u) - w (x)}{α}]} \\ = [lim_{α \to 0} \frac{v (x + α u) - v (x)}{α}] \cdot [lim_{α \to 0} w (x + α u)] + v (x) \cdot [lim_{α \to 0} \frac{w (x + α u) - w (x)}{α}] \\ = \frac{\partial v}{\partial x} u \cdot w + v \cdot \frac{\partial w}{\partial x} u \\ = (grad v) u \cdot w + v \cdot (grad w) u \\ = {(grad v)}^{T} w \cdot u + {(grad w)}^{T} v \cdot u \\ = [{(grad v)}^{T} w + {(grad w)}^{T} v] \cdot u . \end{array}$

si227_e

Since the vector u is arbitrary, it follows that grad (v · w) = (grad v)^Tw + (grad w)^Tv.

The curl of a vector v is defined by

$(curl v) \times a = [grad v - {(grad v)}^{T}] a .$

(2.100)

We can show that the divergence of the curl of a vector v vanishes, i.e.,

$div (curl v) = 0 .$

(2.101)

Also,

$curl (v \times w) = (grad v) w - (grad w) v + v (div w) - w (div v) .$

(2.102)

Note that a useful property of the gradient, divergence, and curl is distributivity over vector and tensor addition, e.g.,

$curl (v + w) = curl v + curl w,$

(2.103a)

$div (A + B) = div A + div B .$

(2.103b)

If $R$ is an open region (volume) bounded by a closed surface $\partial R$ , and φ, v, and A are smooth functions of position, then, according to the divergence theorem,

$\int_{R} grad φ d v = \int_{\partial R} φ n d a, \int_{R} div v d v = \int_{\partial R} v \cdot n d a, \int_{R} div A d v = \int_{\partial R} An d a,$

(2.104)

where dv is the volume element of $R$ , da is the area element of $\partial R$ , and n is the outward unit normal on $\partial R$ . It follows that (refer to Problem 2.52)

$\int_{\partial R} v \cdot An d a = \int_{R} (A \cdot grad v + v \cdot div A) d v .$

(2.105)

Problem 2.52

Prove in direct notation that $\int_{\partial R} v \cdot A n d a = \int_{R} (A \cdot grad v + v \cdot div A) d v .$ si228_e

Solution

Recall that $R$ is an open volume bounded by a closed surface $\partial R$ , dv is the volume element of $R$ , da is the area element of $\partial R$ , and n is the outward unit normal on $\partial R$ . We have

$\begin{array}{l} \int_{\partial R} v \cdot A n d a & = \int_{\partial R} v \cdot {(A^{T})}^{T} n d a = \int_{\partial R} A^{T} v \cdot n d a \\ = \int_{R} div (A^{T} v) d v = \int_{\partial R} (A \cdot grad v + v \cdot div A) d v . \end{array}$

si234_e

Note that we have used result (2.99)₄.

2.5.3 Tensor calculus in cartesian component form

The Cartesian component form of the chain rule (2.95) is

$\begin{array}{l} \frac{d}{d t} φ (T (t), x (t), t) & = \frac{\partial φ}{\partial T_{ij}} \frac{d T_{ij}}{d t} + \frac{\partial φ}{\partial x_{j}} \frac{d x_{i}}{d t} + \frac{\partial φ}{\partial t}, \\ \frac{d}{d t} v_{i} (T (t), x (t), t) & = \frac{\partial v_{i}}{\partial T_{jk}} \frac{d T_{jk}}{d t} + \frac{\partial v_{i}}{\partial x_{j}} \frac{d x_{j}}{d t} + \frac{\partial v_{i}}{\partial t}, \\ \frac{d}{d t} A_{ij} (T (t), x (t), t) & = \frac{\partial A_{ij}}{\partial T_{kl}} \frac{d T_{kl}}{d t} + \frac{\partial A_{ij}}{\partial x_{k}} \frac{d x_{k}}{d t} + \frac{\partial A_{ij}}{\partial t} . \end{array}$

si470_e (2.106)

It can be shown (refer to Problems 2.53–2.57) that

${(grad φ)}_{i} = \frac{\partial φ}{\partial x_{i}} \equiv φ_{i}, {(grad v)}_{ij} = \frac{\partial v_{i}}{\partial x_{j}} \equiv v_{i, j}, {(grad A)}_{ijk} = \frac{\partial A_{ij}}{\partial x_{k}} \equiv A_{ij, k}, div v = \frac{\partial v_{i}}{\partial x_{i}} = v_{i, i}, {(div A)}_{i} = \frac{\partial A_{ij}}{\partial x_{j}} = A_{ij, j} .$

si471_e (2.107)

Then, it follows that the Cartesian component form of the divergence theorem is

$\int_{R} φ_{i} d v = \int_{\partial R} φ n_{i} d a, \int_{R} v_{i, i} d v = \int_{\partial R} v_{i} n_{i} d a, \int_{R} A_{ij, j} d v = \int_{\partial R} A_{ij} n_{j} d a .$

si472_e (2.108)

The Cartesian component form of the curl of a vector v is

${(curl v)}_{i} = ε_{ijk} v_{k, j} .$

(2.109)

Problem 2.53

Prove that (grad φ)_i = φ_,i (i.e., the Cartesian components of grad φ are φ_,i).

Solution

Note that the gradient of a scalar φ is a vector. Its Cartesian components are

${(grad φ)}_{i} = (grad φ) \cdot e_{i} = \frac{\partial φ}{\partial x} \cdot e_{i} = lim_{α \to 0} \frac{1}{α} [φ (x + α e_{i}) - φ (x)] = \frac{\partial φ}{\partial x_{i}} \equiv φ_{, i} .$

si235_e

Thus,

$grad φ = φ_{, i} e_{i} = φ_{, 1} e_{1} + φ_{, 2} e_{2} + φ_{, 3} e_{3} .$

Problem 2.54

Prove that (grad v)_ij = v_i_,j (i.e., the Cartesian components of grad v are v_i_,j).

Solution

Note that the gradient of a vector v is a tensor. Its Cartesian components are

$\begin{array}{l} {(grad v)}_{ij} & = e_{i} Â• (grad v) e_{j} = e_{i} Â• \frac{âˆ‚ v}{âˆ‚ x} e_{j} = e_{i} Â• [lim_{Î± â†’ 0} \frac{v (x + Î± e_{j}) âˆ’ v (x)}{Î±}] \\ = e_{i} Â• \frac{âˆ‚ v}{âˆ‚ x_{j}} = \frac{âˆ‚}{âˆ‚ x_{j}} (e_{i} Â• v) = \frac{âˆ‚ v_{i}}{âˆ‚ x_{j}} â‰¡ v_{i, j} . \end{array}$

si237_e

Thus,

$grad v = v_{i, j} e_{i} \otimes e_{j} = v_{1, 1} e_{1} \otimes e_{1} + v_{1, 2} e_{1} \otimes e_{2} + v_{1, 3} e_{1} \otimes e_{3} + v_{2, 1} e_{2} \otimes e_{1} + v_{2, 2} e_{2} \otimes e_{2} + v_{2, 3} e_{2} \otimes e_{3} + v_{3, 1} e_{3} \otimes e_{1} + v_{3, 2} e_{3} \otimes e_{2} + v_{3, 3} e_{3} \otimes e_{3}$

and

$[grad v] = [\begin{array}{l} v_{1, 1} & v_{1, 2} & v_{1, 3} \\ v_{2, 1} & v_{2, 2} & v_{2, 3} \\ v_{3, 1} & v_{3, 2} & v_{3, 3} \end{array}] .$

si239_e

Problem 2.55

Verify that (grad A)_ijk = A_ij_,k.

Solution

Note that the gradient of a tensor A is a third-order tensor. Hence, according to (2.80), its Cartesian components are

${(grad A)}_{ijk} = (e_{i} \otimes e_{j}) \cdot [(grad A) e_{k}] .$

Then,

$\begin{array}{l} {(grad A)}_{ijk} & = (e_{i} \otimes e_{j}) \cdot (\frac{\partial A}{\partial x} e_{k}) & (definition {(2.96)}_{3}) \\ = (e_{i} \otimes e_{j}) \cdot {lim_{α \to 0} \frac{1}{α} [A (x + α e_{k}) - A (x)]} & (definition {(2.93)}_{2}) \\ = (e_{i} \otimes e_{j}) \cdot \frac{\partial A}{\partial x_{k}} & (definition of partial derivative) \\ = \frac{\partial}{\partial x_{k}} [A \cdot (e_{i} \otimes e_{j})] & (e_{i} and e_{j} independent of x_{k}) \\ = \frac{\partial}{\partial x_{k}} tr [A {(e_{i} \otimes e_{j})}^{T}] & (definition (2.41)) \\ = \frac{\partial}{\partial x_{k}} tr [A (e_{j} \otimes e_{i})] & (result {(2.20)}_{1}) \\ = \frac{\partial}{\partial x_{k}} tr [(A e_{j}) \otimes e_{i}] & (result {(2.20)}_{2}) \\ = \frac{\partial}{\partial x_{k}} (e_{i} \otimes A e_{j}) & (definition {(2.38)}_{3}) \\ = \frac{\partial A_{ij}}{\partial x_{k}} & (definition (2.29)) \\ \equiv A_{ij, k} . \end{array}$

si241_e

Thus, grad A = A_ij_,ke_i ⊗ e_j ⊗ e_k.

Problem 2.56

Show that div v = v_i_,i.

Solution

Note that the divergence of a vector v is a scalar. Using definition (2.97) and the result grad v = v_i_,je_i ⊗ e_j from Problem 2.54, we have

$div v = tr (grad v) = tr (v_{i, j} e_{i} \otimes e_{j}) = v_{i, j} tr (e_{i} \otimes e_{j}) = v_{i, j} (e_{i} \cdot e_{j}) = v_{i, j} δ_{ij} = v_{i, i} .$

Expanding this result, we obtain

$div v = v_{i, i} = v_{1, 1} + v_{2, 2} + v_{3, 3} .$

Problem 2.57

Prove that (div A)_i = A_ij_,j.

Solution

The divergence of a tensor A is a vector. The ith component of this vector is

${(div A)}_{i} = (div A) \cdot e_{i} = div (A^{T} e_{i}),$

where we have used definition (2.24) of the Cartesian component of a vector and definition (2.98) of the divergence of a tensor. Then

$div (A^{T} e_{i}) = div [(A_{kj} e_{j} \otimes e_{k}) e_{i}] = div [A_{kj} (e_{k} \cdot e_{i}) e_{j}] = div (A_{kj} δ_{ki} e_{j}) = div (A_{ij} e_{j}) .$

Recalling that div v = div (v_ie_i) = v_i_,i from Problem 2.56, we deduce by analogy that div (A_ije_j) = A_ij_,j. Thus,

${(div A)}_{i} = A_{ij, j},$

$div A = {(div A)}_{i} e_{i} = A_{ij, j} e_{i} = (A_{11, 1} + A_{12, 2} + A_{13, 3}) e_{1} + (A_{21, 1} + A_{22, 2} + A_{23, 3}) e_{2} + (A_{31, 1} + A_{32, 2} + A_{33, 3}) e_{3} .$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 2.3 Eigenvalues, eigenvectors, polar decomposition, invariants

Create new playlist

Sign In

Sign Up

2.2.7 Vector product, scalar triple product

2.3 Eigenvalues, eigenvectors, polar decomposition, invariants

2.4 Tensors of order three and four

2.5 Tensor calculus

2.5.1 Partial derivatives

2.5.2 Chain rule, gradient, divergence, curl, divergence theorem

2.5.3 Tensor calculus in cartesian component form

Table of Contents for
2.3 Eigenvalues, eigenvectors, polar decomposition, invariants