Optimization basically involves either minimizing or maximizing some function, f(x), where x is a numerical vector or a scalar. Here, f(x) is called the objective function or criterion. In the context of neural networks, we call it the cost function, loss function, or error function. In the previous example, the loss function we want to minimize is E.

Suppose we have a function, y = f(x), where x and y are real numbers. The derivative of this function tells us how this function changes with small changes to x. So, the derivative can be used to reduce the value of the function by infinitesimally changing x. Suppose f'(x) > 0 at x. This means f(x) will increase if we increase x along positive x and hence f(x - ε) < f(x) for small enough ε. Note f(x) can be reduced by moving x in small steps within the opposite direction of the derivative:

If the derivative f'(x) = 0, then the derivative provides no information in which direction we need to move to reach the function minimum. The derivative can be zero at a local optimum (minimum/maximum). A point, x*, is called local minimum if the value of the function, f(x), at x* is less than all neighboring points of x*. Similarly, we can define a local maximum. Some points can be neither maximum nor minimum, but the derivative f'(x) is zero at those points. These are called saddle points. The following figure explains the three scenarios where f'(x) = 0:

A point that attains lowest value of f among all possible values of x is called a global minimum. A function can have one or many global minima. There could be local minima that are not a global minimum. However, if the function is convex, it's guaranteed that it has only one global minimum and no local minima. 

Generally in ML, we are interested in minimizing a real valued function of several variables f: . A simple example of a real valued function of several variables is the hotplate temperature function,  at a point with coordinates  on the plate. In deep learning, we generally minimize a loss function, which is a function of several variables, such as the weights in the neural network. These functions have many local minima, many saddle points that are surrounded by very flat regions, and they may or may not have any global minima. All this makes it very difficult to optimize such functions.

The derivatives of a function of several variables are expressed as partial derivatives, which measure the rate of change of the function as we change one of the input variables, x_i, keeping all other input variables constant. The vector of partial derivatives with regards to all the variables is called the gradient vector of f and is denoted by ∇f. We can also find out how fast the function might be changing with respect to some arbitrary direction,  (a unit vector). This is computed by projecting the gradient vector, ∇f, in the direction of the unit vector, , that is, the dot product, . This is called the directional derivative of f in the direction of  and is often denoted by . To minimize f, we need to find a direction, , in which to change , such that the value of f is reduced maximally. 

Let  be a point very close to , that is,  is very small. First, the order expansion of the Taylor series around 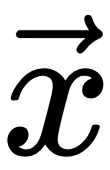 is given by:

The last term in the preceding equation is negligible for  to be close enough to  . The second term represents the directional derivative of f along . Here we have:

Therefore,  is maximally reduced if cos (θ) is minimum, that is, -1, which will happen if θ = π, that is,  should point in a direction opposite to the gradient vector, ∇f. This is the direction of steepest descent:  or the direction of steepest gradient descent. We explain this in the following figure: 

The Hot plate example: the temperature at a given coordinate (x and y) is given by the function f (x, y) = 50 -y² - 2x² . The plate is hottest at the center (0, 0), with a temperature of 50. The gradient vector at a point (x, y) is given by ∇f = (-4x, -2y). The temperature at point (2.3, 2) on the plate is 40. This point lies on a contour of constant temperature. Clearly, moving in a direction opposite to the gradient, as shown by the red arrow, with step size ε the temperature reduces to 30.

Let's implement gradient-descent optimization for the hot plate temperature function using tensorflow. We need to initialize the gradient descent, so let's start at x = y = 2:

import tensorflow as tf
#Initialize Gradient Descent at x,y =(2, 2)
x = tf.Variable(2, name='x', dtype=tf.float32)
y = tf.Variable(2, name='y', dtype=tf.float32)

temperature = 50 - tf.square(y) - 2*tf.square(x)

#Initialize Gradient Descent Optimizer
optimizer = tf.train.GradientDescentOptimizer(0.1) #0.1 is the learning rate
train = optimizer.minimize(temperature)
grad = tf.gradients(temperature, [x,y]) #Lets calculate the gradient vector

init = tf.global_variables_initializer()
with tf.Session() as session:
    session.run(init)    
    print("Starting at coordinate x={}, y={} and temperature there is 
            {}".format(
                   session.run(x),session.run(y),session.run(temperature)))
    grad_norms = []
    for step in range(10): 
        session.run(train)
        g = session.run(grad)
        print("step ({}) x={},y={}, T={}, Gradient={}".format(step,  
                     session.run(x), session.run(y), session.run(temperature), g))
        grad_norms.append(np.linalg.norm(g))

plt.plot(grad_norms)

The following is the output of the preceding code. In each step, new values of x, y are calculated as suggested by the gradient vector such that the overall temperature decreases maximally. Note that the gradient calculated exactly matches the formula stated previously. We are also calculating the gradient norm after each step. Here is how the gradient changes in 10 iterations:

Starting at coordinate x=2.0, y=2.0 and temperature there is 38.0
step (0)  x=2.79,y=2.40000, T=28.55, Gradient=[-11.2, -4.8000002]
step (1)  x=3.92,y=2.88000, T=10.97, Gradient=[-15.68, -5.7600002]
..........
step (9)  x=57.85,y=12.38347, T=-6796.81, Gradient=[-231.40375, -24.766947]