For training deep multilayered neural networks, we can still use the gradient decent/SGD. But, SGD will require computing the derivatives of the loss function with regards to all the weights of the network. We have seen how to apply the chain rule of derivatives to compute the derivative for the logistic unit.

Now, for a deeper network, we can recursively apply the same chain rule layer by layer to obtain the derivative of the loss function with regards to the weights corresponding to layers at different depths in the network. This is called the backpropagation algorithm. 

Backpropagation was invented in the 1970s as a general optimization method for performing automatic differentiation of complex nested functions or functions of a function. However, it wasn't until 1986, with the publishing of a paper by Rumelhart, Hinton, and Williams, titled Learning representations by back-propagating errors (https://www.iro.umontreal.ca/~vincentp/ift3395/lectures/backprop_old.pdf), that the importance of the algorithm was appreciated by the greater ML community. Backpropagation was one of the first methods able to demonstrate that artificial neural networks could learn good internal representations; that is, their hidden layers learned nontrivial features. 

The backpropagation algorithm is an efficient way of computing the error derivative, , for every weight on a single training example. To understand the backpropagation algorithm, let's first represent a neural network with a computational graph notation. A computational graph of a neural network will have nodes and directed edges, where the nodes represent variables (tensors) and the edges represent operations on variables connecting to the next variable. A variable, x, is connected to y by a directed edge if y = f(x), for some function, f.

For example, the graph for the logistic unit can be represented as follows:

We represent the computation nodes by u¹, u², ..., uⁿ. Also, we arrange the nodes in order so that they can be computed one after the other. Here, uⁿ is a scalar—the loss function. Let's denote the parameters or weights of the network by nodes, . To apply gradient descent, we need to compute all the derivatives, . The forward computation for this graph can be calculated by following the directed path in the computation graph from input nodes to the final node, . This is called forward pass.

Since the nodes in our graphs are tensors, to compute the partial derivatives, 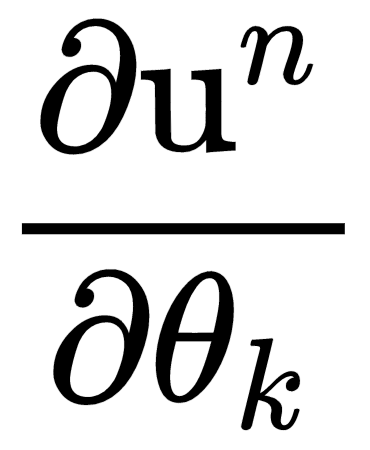, the chain rule of derivatives for functions of several variables will be used, which is represented by a multiplication of a Jacobian with a gradient. The backpropagation algorithm involves a sequence of such Jacobian-Gradient products.

Backpropagation algorithm is represented as follows:

1. Given input vectors, , target vectors, , a cost function C to measure network error, and a set of initial weights of a network, compute a forward pass of the network and calculate loss, C

2. Backward pass—for each training example , calculate the derivative of loss, C, with respect to each layer parameters/weights—this step is discussed as follows:
   1. Combine individual gradients by taking an average over all the gradients for the input-target pairs or a mini-batch of them
   2. Update each of the parameters, , α being the learning rate

We will explain backward pass with a fully connected three-layered neural network. The computation graph for this is shown in the preceding figure. Let z⁽ⁱ⁾ represent a computation node in the graph. To perform backpropagation, the computation of derivative  will proceed in exactly the reverse order of the forward pass. These are indicated by the downward arrows. Let’s denote the derivative of the cost function with regards to the layer l input z^(l) z^(l) by . For the topmost layer, let . To compute recursively, let's consider a single layer. A layer has an input, z^(l), and output, z^(l+1). Also, the layer will take input and produce and .

For layer l,

i represents the i^th component of the gradient . 

Thus, we arrive at a recursive formula for computing the backward messages. Using these, we can also compute the derivative of the cost with regards to the model parameters, as follows: 

The backpropagation algorithm computes the gradient of the scalar cost function, z, with respect to its ancestor, x, in the computation graph. The algorithm begins by computing the derivative of the cost, z, with regards to itself, . The gradient with regards to the parent of z can be computed by multiplying the current gradient by the Jacobian of the operation that produced z. We keep traversing the compute graph backwards and multiplying the Jacobians until we reach the input, x.