Chapter 14

Analysis of Variance and Experimental Designs

Learning Objectives

Upon completion of this chapter, you will be able to:

• Understand the concept of ANOVA and experimental designs
• Compute and interpret the result of completely randomized design (one-way ANOVA)
• Compute and interpret the result of randomized block design
• Compute and interpret the result of factorial design (two-way ANOVA)

14.1 Introduction

In the previous chapter, we discussed the various techniques of analysing data from two samples (taken from two populations). These techniques were related to means and proportions. In real life, there may be situations when instead of comparing two sample means, a researcher has to compare three or more than three sample means (specifically, more than two). A researcher may have to test whether the three or more sample means computed from the three populations are equal. In other words, the null hypothesis can be, that three or more population means are equal as against the alternative hypothesis that these population means are not equal. For example, suppose that a researcher wants to measure work attitude of the employees in four organizations. The researcher has prepared a questionnaire consisting of 10 questions for measuring the work attitude of employees. A five-point rating scale is used with 1 being the lowest score and 5 being the highest score. So, an employee can score 10 as the minimum score and 50 as the maximum score. The null hypothesis can be set as all the means are equal (there is no difference in the degree of work attitude of the employees) as against the alternative hypothesis that at least one of the means is different from the others (there is a significant difference in the degree of work attitude of the employees).

14.2 Introduction to Experimental Designs

An experimental design is the logical construction of an experiment to test hypothesis in which the researcher either controls or manipulates one or more variables. Some of the widely used terms while discussing experimental designs are as follows:

Independent variable: In an experimental design, the independent variable may be either a treatment variable or a classification variable.

Treatment variable: This is a variable which is controlled or modified by the researcher in the experiment. For example, in agriculture, the different fertilizers or the different methods of cultivation are the treatments.

Classification variable: Classification variable can be defined as the characteristics of the experimental subject that are present prior to the experiment and not a result of the researcher’s manipulation or control.

Experimental Units: The smallest division of the experimental material to which treatments are applied and observations are made are referred to as experimental units.

Dependent variable: In experimental design, a dependent variable is the response to the different levels of independent variables. This is also called response variable.

Factor: A factor can be referred to as a set of treatments of a single type. In most situations, a researcher may be interested in studying more than one factor. For example, a researcher in the field of advertising may be interested in studying the impact of colour and size of advertisements on consumers. In addition, the researcher may be interested in knowing the difference in average responses to three different colours and four different sizes of the advertisement. This is referred to as two-factor ANOVA.

14.3 Analysis of Variance

Analysis of variance or ANOVA is a technique of testing hypotheses about the ­significant difference in several population means. This technique was developed by R. A. Fisher. In this chapter, experimental designs will be analysed by using ANOVA. The main purpose of analysis of variance is to detect the difference among various population means based on the information gathered from the samples (sample means) of the respective populations.

Analysis of variance is also based on some assumptions. Each population should have a normal distribution with equal variances. For example, if there are n populations, variances of each population, that is, Each sample taken from the population should be randomly drawn and should be independent of each other.

In analysis of variance, the total variation in the sample data can be on account of two components, namely, variance between the samples and variance within the samples. Variance between samples is attributed to the difference among the sample means. This variance is due to some assignable causes. Variance within the samples is the difference due to chance or experimental errors. For the sake of clarity, the techniques of analysis of variance can be broadly classified into one-way classification and two-way classification. In fact, many different types of experimental designs are available to the researchers. This chapter will focus on three specific types of experimental designs, namely, completely randomized design, randomized block design, and factorial design. ANOVA is based on the following assumptions:

• Samples are drawn from normally distributed populations.
• Samples are randomly drawn from populations and are independent of each other.
• Populations from which samples are drawn have equal variances.

14.4 Completely randomized design (One-way ANOVA)

Completely randomized design contains only one independent variable, with two or more treatment levels or classifications. In case of only two treatment levels or classifications, the design would be the same as that used for hypothesis testing for two populations in Chapter 13. When there is a case of three or more classification levels, analysis of variance is used to analyse the data.

Suppose a researcher wants to test the stress level of employees in three different organizations. For conducting this research, he has prepared a questionnaire with a five-point rating scale with 1 being the minimum score and 5 being the maximum score. The researcher has administered the questionnaire and obtained the mean score for three organizations. The researcher could have used the z-test or t test for two populations if there had been only two populations. In this case, there are three populations, so there is no scope of using z-test or t test for testing the hypotheses. In this case, one-way analysis of variance technique can be effectively used to analyse the data. One-way analysis of variance can also be used very effectively in the case of comparison among sample means taken from more than two populations.

Suppose if k samples are being analysed by a researcher, then the null and alternative hypotheses can be set as below:

H₀: μ₁ = μ₂= μ₃= … = μ_k

The alternative hypothesis can be set as below:

H₁: Not all μ_js are equal (j = 1, 2, 3, …, k )

The null hypothesis indicates that all population means for all levels of treatments are equal. If one population mean is different from another, the null hypothesis is rejected and the alternative hypothesis is accepted.

In one-way analysis of variance, testing of hypothesis is carried out by partitioning the total variation of the data in two parts. The first part is the variance between the samples and the second part is the variance within the samples. The variance between the samples can be attributed to treatment effects and variance within the samples can be attributed to experimental errors. As part of this process, the total sum of squares can be divided into two additive and independent parts as shown in Figure 14.1:

FIGURE 14.1 Partitioning the total sum of squares of the variation for completely randomized design (one-way ANOVA)

SST (total sum of squares) = SSC (sum of squares between columns) + SSE (sum of squares within samples)

14.4.1 Steps in Calculating SST (Total Sum of Squares) and Mean Squares in One-Way Analysis of Variance

TABLE 14.3 Observations obtained for k independent samples based on one-criterion classification

As discussed above, the total sum of squares can be partitioned in two parts: sum of squares between columns and sum of squares within samples. So, there are two steps in calculating SST (total sum of squares) in one-way analysis of variance, in terms of calculating sum of squares between columns and sum of squares within samples. Let us say that the observations obtained for k independent samples is based on one-criterion classification and can be arranged as shown in the Table 14.3 above:

where

and

1. 1. Calculate variance between columns (samples): This is usually referred to as sum of squares between samples and is usually denoted by SSC. The variance between columns measures the difference between the sample mean of each group and the grand mean. Grand mean is the overall mean and can be obtained by adding all the individual observations of the columns and then dividing this total by the total number of observations. The procedure of calculating the variance between the samples is as below:
   1. In the first step, we need to calculate the mean of each sample. From Table 14.3, the means are
   2. Next, the grand mean is calculated. The grand mean is calculated as

      

   3. In Step 3, the difference between the mean of each sample and grand mean is calculated, that is, we calculate .
   4. In Step 4, we multiply each of these by the number of observations in the corresponding sample, square each of these deviations and add them. This will give the sum of the squares between samples.
   5. In the last step, the total obtained in Step 4 is divided by the degrees of freedom. The degrees of freedom is one less than the total number of samples. If there are k samples, the degrees of freedom will be v = k – 1. When the sum of squares obtained in Step 4 is divided by the number of degrees of freedom, the result is called mean square (MSC) and is an alternative term for sample variance.

      SSC (sum of squares between columns) =

      where k is the number of groups being compared, n_j the number of observations in Group j , the sample mean of Group j , and the grand mean.

      and MSC (mean square) =

      where SSC is the sum of squares between columns and k – 1 the degrees of freedom (number of samples – 1).

2. 2. Calculate variance within columns (samples): This is usually referred to as the sum of squares within samples. The variance within columns (samples) measures the difference within the samples (intra-sample difference) due to chance. This is usually denoted by SSE. The procedure of calculating the variance within the samples is as below:

   The variance within columns (samples) measures the difference within the samples (intra-sample difference) due to chance. This is usually denoted by SSE.

   1. In calculating the variance within samples, the first step is to calculate the mean of each sample. From Table 14.3 this is
   2. Second step is to calculate the deviation of each observation in k samples from the mean values of the respective samples.
   3. As a third step, square all the deviations obtained in Step 2 and calculate the total of all these squared deviations.
   4. As the last step, divide the total squared deviations obtained in Step 3 by the degrees of freedom and obtain the mean square. The number of degrees of freedom can be calculated as the difference between the total number of observations and the number of samples. If there are n observations and k samples then the degrees of freedom is v = n – k

      SSE (sum of squares within samples) =

      where x_ij is the ith observation in Group j , the sample mean of Group j , k the number of groups being compared, and n the total number of observations in all the groups.

      and MSE (mean square) =

      where SSE is the sum of squares within columns and n – k the degrees of freedom (total number of observations – number of samples).

3. 3. Calculate total sum of squares: The total variation is equal to the sum of the squared difference between each observation (sample value) and the grand mean . This is often referred to as SST (total sum of squares). So, the total sum of squares can be calculated as below:

   The total variation is equal to the sum of the difference between each observation (sample value) and the grand mean This is often referred to as SST (total sum of squares).

   SST (total sum of squares) = SSC (sum of squares between columns) + SSE (sum of squares within samples)

   

   SST (total sum of squares) =

   where x_ij is the ith observation in Group j , the grand mean, k the number of groups being compared, and n the total number of observations in all the groups

   and MST (mean square) =

   where SST is the total sum of squares and

   n – 1 the degrees of freedom (number of observations – 1).

14.4.2 Applying the F - Test Statistic

As discussed, ANOVA can be computed with three sums of squares: SSC (sum of squares between columns), SSE (sum of squares within samples), and SST (total sum of squares). As discussed in the previous chapter (Chapter 13), F is the ratio of two variances.

In case of ANOVA, F value is obtained by dividing the treatment variance (MSC) by the error variance (MSE). So, in case of ANOVA, F value is calculated as below:

F test statistic in one-way ANOVA

where MSC is the mean square column and MSE the mean square error.

The F test statistic follows F distribution with k – 1 degrees of freedom corresponding to MSC in the numerator and n – k degrees of freedom corresponding to MSE in the denominator. The null hypothesis is rejected if the calculated value of F is greater than the upper-tail critical value F_U with k – 1 degrees of freedom in the numerator and n – k degrees of freedom in the denominator. For a given level of significance α, the rules for acceptance or rejection of the null hypothesis are shown below:

For a given level of significance α, the rules for acceptance or rejection of the null hypothesis

Reject H₀, if calculated F > F_U (Upper tail value of F),

otherwise do not reject H₀.

Figure 14.2 exhibits the rejection and non-rejection region (acceptance region) when using ANOVA to test the null hypothesis.

FIGURE 14.2 Rejection and non-rejection region (acceptance region) when using ANOVA to test null hypothesis

14.4.3 The ANOVA Summary Table

The result of ANOVA is usually presented in an ANOVA table (shown in Table 14.4). The entries in the table consist of SSC (sum of squares between columns), SSE (sum of squares within samples) and SST(total sum of squares); corresponding degrees of freedom k – 1, n – k and, n – 1; MSC (mean square column) and MSE (mean square error); and F value. When using software programs such as MS Excel, Minitab, and SPSS, the summary table also includes the p value. The p value allows a researcher to make inferences directly without taking help from the critical values of the F distribution.

TABLE 14.4 ANOVA Summary Table

Example 14.1

Vishal Foods Ltd is a leading manufacturer of biscuits. The company has launched a new brand in the four metros; Delhi, Mumbai, Kolkata, and Chennai. After one month, the company realizes that there is a difference in the retail price per pack of biscuits across cities. Before the launch, the company had promised its employees and newly-appointed retailers that the biscuits would be sold at a uniform price in the country. The difference in price can tarnish the image of the company. In order to make a quick inference, the company collected data about the price from six randomly selected stores across the four cities. Based on the sample information, the price per pack of the biscuits (in rupees) is given in Table 14.5:

TABLE 14.5 Price per pack of the biscuits (in rupees)

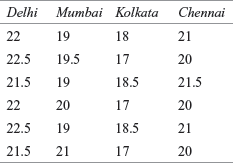
Use one-way ANOVA to analyse the significant difference in the prices. Take 95% as the confidence level.

Soultion

The seven steps of hypothesis testing can be performed as below:

Step 1: Set null and alternative hypotheses

The null and alternative hypothesis can be stated as below:

and H₁: All the means are not equal

Step 2: Determine the appropriate statistical test

The appropriate test statistic is F test statistic in one-way ANOVA given as below

where MSC = mean square column

MSE = mean square error

Step 3: Set the level of significance

Alpha has been specified as 0.05.

Step 4: Set the decision rule

For a given level of significance 0.05, the rules for acceptance or rejection of null hypothesis are as follows:

Reject H₀ if calculated F > F_U (upper-tail value of F),

otherwise, do not reject H₀.

In this problem, for the numerator and the denominator the degrees of freedom are 3 and 20 respectively. The critical F-value is F_{0.05, 3, 20} = 3.10.

Step 5: Collect the sample data

The sample data is as shown in Table 14.6.

TABLE 14.6 Sample data for Example 14.1

Step 6: Analyse the data

From the table

;

and n₁ = n₂ = n₃ = n₄ = 6

SSC (sum of squares between columns) =

= 25.0104 + 0.8437 + 31.5104 + 2.3437 = 59.7083

SSE (sum of squares within samples) =

= 9.25

SST (total sum of squares) =

= 68.9583

MSE (mean square) =

Table 14.7 exhibits the ANOVA table for Example 14.1

TABLE 14.7 ANOVA table for Example 14.1

Step 7: Arrive at a statistical conclusion and business implication

At 95% confidence level, the critical value obtained from the F table is F_{0.05, 3, 20} = 3.10. The calculated value of F is 43.03, which is greater than the tabular value (critical value) and falls in the rejection region. Hence, the null hypothesis is rejected and the alternative hypothesis is accepted.

There is enough evidence to believe that there is a significant difference in the prices across four cities. So, the management must initiate corrective steps to ensure that the prices should remain uniform. This must be done urgently to protect the credibility of the firm.

Self-Practice Problems

14A1. Use the following data to perform one-way ANOVA

Use α = 0.05 to test the hypotheses for the difference in means.

14A2. Use the following data to perform one-way ANOVA

Use α = 0.01 to test the hypotheses for the difference in means.

14A3. A company is in the process of launching a new product. Before launching, the company wants to ascertain the status of its product as a second alternative. For doing so, the company prepared a questionnaire consisting of 20 questions on a five-point rating scale with 1 being “strongly disagree” and 5 being “strongly agree.” The company administered this questionnaire to 8 randomly selected respondents from five potential sales zones. The scores obtained from the respondents are given in the table. Use one-way ANOVA to analyse the significant difference in the scores. Take 90% as the confidence level.

14.5 Randomized Block Design

We have already discussed that in one-way ANOVA the total variation is divided into two components: variations between the samples or columns, due to treatments and variation within the samples, due to error. There is a possibility that some of the variation, which was attributed to random error may not be due to random error, but may be due to some other measurable factors. If this measurable factor is included in the MSE, it will result in an increase in the MSE. Any increase in the MSE would result in a small F value (MSE being a denominator in the F-value formula), which would ultimately lead to the acceptance of the null hypothesis.

Like the completely randomized design, randomized block design also focuses on one independent variable of interest (treatment variable). Additionally, in randomized block design, we also include one more variable referred to as “blocking variable.” This blocking variable is used to control the confounding variable. Confounding variables, though not controlled by the researcher, can have an impact on the outcome of the treatment being studied. In Example 14.1, the selling price was different in the four metros. In this example, some other variable which is not controlled by the researcher may have an impact on the varying prices. This may be the tax policy of the state, transportation cost, etc. By including these variables in the experimental design, the possibility of controlling these variables can be explored. The blocking variable is a variable which a researcher wants to control but is not a treatment variable of interest. The term blocking has an agriculture origin where “blocking” refers to a block of land. For example, if we apply blocking in Example 14.1, under a given circumstance, each set of the four prices related to four metropolitan cities will constitute a block of sample data. Blocking provides the opportunity for a researcher to compare prices one to one.

In case of a randomized block design, variation within the samples can be partitioned into two parts as shown in Figure 14.3.

Figure 14.3 Partitioning the SSE in randomized block design

So, in randomized block design, the total sum of squares consists of three parts:

SST (total sum of squares) = SSC (sum of squares between columns) + SSR (sum of squares between rows) + SSE (sum of squares of errors)

14.5.1 Null and Alternative Hypotheses in a Randomized Block Design

It has already been discussed that in a randomized block design the total sum of squares consists of three parts. In light of this, the null and alternative hypotheses for the treatment effect can be stated as below:

Suppose if c samples are being analysed by a researcher then null hypothesis can be stated as:

The alternative hypothesis can be set as below:

H₁: All treatment means are not equal

For blocking effect, the null and alternative hypotheses can be stated as below (when r rows are being analysed by a researcher):

The alternative hypothesis can be set as below:

H₁: All blocking means are not equal

Formulas for calculating SST (total sum of squares) and mean squares in a randomized block design

SSC (sum of squares between columns) =

where c is the number of treatment levels (columns), r the number of observations in each treatment level (number of blocks), the sample mean of Group j (Column means), and the grand mean

and MSC(mean square) =

where SSC is the sum of squares between columns and c – 1 the degrees of freedom (number of columns – 1).

SSR (sum of squares between rows) =

where c is the number of treatment levels (columns), r the number of observations in each treatment level (number of blocks), the sample mean of Group i (row means), and the grand mean

and MSR(mean square) =

where SSE is the sum of squares within columns, and r – 1 the degrees of freedom (number of rows – 1).

SSE (sum of squares of errors) =

where c is the number of treatment levels (columns), r the number of observations in each treatment level (number of blocks), the sample mean of Group i (row means), x_j the sample mean of Group j (column means), x_ij the ith observation in Group j , and the grand mean

and MSE (mean square) =

where SSE is the sum of squares of errors and n – r – c = (c – 1)(r – 1) = degrees of freedom (number of observations – number of rows – number of columns = n = number of observations.

14.5.2 Applying the F-Test Statistic

As discussed, the total sum of squares consists of three parts: SST(total sum of squares) = SSC (sum of squares between columns) + SSR (sum of squares between rows) + SSE (sum of squares of errors)

In case of two-way ANOVA, F value can be obtained as below:

F-test statistic in randomized block design

where MSC is the mean square column and MSE the mean square error.

with c – 1, degrees of freedom for numerator

n – r – c = (c – 1)(r – 1), degrees of freedom for denominator

and

where MSR is the mean square row and MSE the mean square error.

with r – 1 = degrees of freedom for numerator and

n – r – c = (c – 1)(r – 1), degrees of freedom for denominator.

For a given level of significance α, rules for acceptance or rejection of null hypothesis are as below:

For a given level of significance α, rules for acceptance or rejection of null hypothesis

Reject H₀ if , F_calculated > F_critical . Otherwise, do not reject H₀.

14.5.3 ANOVA Summary Table for Two-Way Classification

The results of ANOVA are usually presented in an ANOVA table (shown in Table 14.8). The entries in the table consist of SSC(sum of squares between columns), SSR (sum of squares between rows), SSE (sum of squares of errors), SST (total sum of squares); corresponding degrees of freedom (c – 1); (r – 1); (c – 1)(r – 1), and (n – 1); MSC (mean square column); MSR (mean square row) and MSE (mean square error); F values in terms of F_treatment and F_block. As discussed, in randomized block design when using software programs such as MS Excel, Minitab, and SPSS, summary table also includes p value. The p value allows a researcher to make inferences directly without taking help from the critical values of the F distribution.

TABLE 14.8 ANOVA Summary table for two-way classification

Example 14.2

A company which produces stationary items wants to diversify into the photocopy paper manufacturing business. The company has decided to first test market the product in three areas termed as the north area, central area, and the south area. The company takes a random sample of five salesmen S1, S2, S3, S4, and S5 for this purpose. The sales volume generated by these five salesmen (in thousand rupees) and total sales in different regions is given in Table 14.9:

TABLE 14.9 Sales volume generated by five salesmen (in thousand rupees) and total sales in different regions (in thousand rupees)

Use a randomized block design analysis to examine:

1. Whether the salesmen significantly differ in performance?

2. Whether there is a significant difference in terms of sales capacity between the regions?

Take 95% as confidence level for testing the hypotheses.

Soultion

The seven steps of hypothesis testing can be performed as below:

Step 1: Set null and alternative hypotheses

The null and alternative hypotheses can be divided into two parts: For treatments (columns) and for blocks (rows).

For treatments (columns), null and alternative hypotheses can be stated as below:

and H₁: All the treatment means are not equal

For blocks (rows), null and alternative hypotheses can be stated as below:

and H₁: All the block means are not equal

Step 2: Determine the appropriate statistical test

F-test statistic in randomized block design

where MSC is the mean square column and MSE the mean square error.

with c – 1, degrees of freedom for numerator

n – r – c = (c – 1)(r – 1), degrees of freedom for denominator

and

where MSR is the mean square row and MSE the mean square error.

with r – 1, degrees of freedom for numerator

n – r – c = (c – 1)(r – 1), degrees of freedom for denominator.

Step 3: Set the level of significance

Let α = 0.05.

Step 4: Set the decision rule

For a given level of significance 0.05, the rules for acceptance or rejection of null hypothesis are as follows

Reject H₀, if F_calculated > F_critical, otherwise do not reject H₀.

For treatments, degrees of freedom = (c – 1) = (5 – 1) = 4

For blocks, degrees of freedom = (r – 1) = (3 –1) = 2

For error, degrees of freedom = (c – 1)(r – 1) = 4 = 8

Step 5: Collect the sample data

Sample data is given in Example 14.2. The treatment means and block means are shown in Table 14.10 as follows:

TABLE 14.10 Treatment means and block means for sales data

 

Step 6: Analyse the data

SSC (sum of squares between columns) =

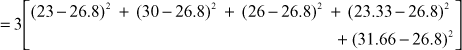
= 183.066

SSR (sum of squares between rows) =

= 5.2

SSE (sum of squares of errors) =

SST (total sum of squares of errors) =

= 200.40

The ANOVA summary table for Example 14.2 is shown in Table 14.11.

TABLE 14.11ANOVA Summary table for Example 14.2

 

Step 7: Arrive at a statistical conclusion and business implication

At 95% confidence level, critical value obtained from the F table is F_{0.05, 4, 8} = 3.84 and F_{0.05, 2, 8} = 4.46.

The calculated value of F for columns is 30.17. This is greater than the tabular value (3.84) and falls in the rejection region. Hence, the null hypothesis is rejected and alternative hypothesis is accepted.

The calculated value of F for rows is 1.71. This is less than the tabular value (4.46) and falls in the acceptance region. Hence, the null hypothesis is accepted and alternative hypothesis is rejected.

There is enough evidence to believe that there is a significant difference in the performance of five salesmen in terms of generation of sales. On the other hand, there is no significant difference in the capacity of generating sales for the three regions. The result that indicates a difference in the sales volume generation capacity of the three regions may be due to chance. Therefore, the management should concentrate on individual salesmen rather than concentrating on regions.

SELF-PRACTICE PROBLEMS

14B1. The table below shows data in the form of a randomized block design.

Use a randomized block design analysis to examine:

(1) Significant difference in the treatment level.

(2) Significant difference in the block level.

Take 95% as confidence level for testing the hypotheses.

14B2. The table below shows data in form of a randomized block design

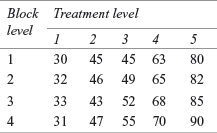
Use a randomized block design analysis to examine:

(1) Significant difference in the treatment level.

(2) Significant difference in the block level.

Take 90% as the confidence level for testing the hypotheses.

14B3. A researcher has obtained randomly selected sales data (in thousand rupees) of four companies: Company 1, Company 2, Company 3, and Company 4. These data are arranged in a randomized block design with respect to company and region. Use a randomized block design analysis to examine:

(1) Significant difference in average sales of four different companies.

(2) Significant difference in average sales of three different regions.

Take α = 0.05 for testing the hypotheses.

14.6 Factorial Design (Two-way ANOVA)

In some real-life situations, a researcher has to explore two or more treatments simultaneously. This type of experimental design is referred to as factorial design. In a factorial design, two or more treatment variables are studied simultaneously. For example, in the previous example, we had discussed the variation in performance of salesmen due to one blocking variable, region. Salesmen performance may also depend upon various other variables such as support provided by the company, attitude of a particular salesman, support from the dealer network, support from the retailer, etc. All these four variables (and many other ­variables depending upon the situation) can be included in the experimental design and can be studied simultaneously. In this section, we will study the factorial design with two treatment variables.

Factorial design has many advantages over completely randomized design. If we use completely randomized design for measuring the effect of two treatment variables, we will have to apply two complete randomized designs. Factorial design provides a platform to analyse both the treatment variables simultaneously in one experimental design. In a factorial design, a researcher can control the effect of multiple treatment variables. In addition, factorial design provides an opportunity to study the interaction effect of two treatment variables. It is important to understand that the randomized block design concentrates on one treatment (column) and control for a blocking effect (row effect). Randomized block design does not provide the opportunity to study the interaction effect of treatment and block. This facility is available only in factorial design.

14.6.1 Null and Alternative Hypotheses in a Factorial Design

A two-way analysis of variance is used to test the hypothesis of a factorial design having two factors. In light of this, the null and alternative hypotheses for the treatment effect can be stated as below:

Row effect: H₀: All the row means are equal.

H₁: All the row means are not equal.

Column effect: H₀: All the column means are equal.

H₁: All the column means are not equal.

Interaction effect: H₀: Interaction effects are zero.

H₁: Interaction effect is not zero (present).

14.6.2 Formulas for Calculating SST (Total Sum of Squares) and Mean Squares in a Factorial Design (Two-Way Analysis of Variance)

SSC (sum of squares between columns) =

where c is the number of column treatments, r the number of row treatments, n the number of observations in each cell, the sample mean of Group j , and the grand mean

and MSC (mean square) =

where SSC is the sum of squares between columns and c – 1 the degrees of freedom (number of columns – 1).

SSR (sum of squares between rows) =

where c is the number of column treatments, r the number of row treatments, n the number of observations in each cell, the sample mean of Group i (row means), and the grand mean

and MSR (mean square) =

where SSR is the sum of squares between rows and r – 1 the degrees of freedom (number of rows – 1).

SSI (sum of squares interaction) =

where c is the number of column treatments, r the number of row treatments, n the number of observations in each cell, the sample mean of Group i (row means), the sample mean of Group j (column means), the mean of the cell corresponding to ith row and jth column (cell mean), and the grand mean

and MSI (mean square) =

where SSI is the sum of squares interaction and (r – 1)(c – 1) the degrees of freedom.

SSE (sum of squares errors) =

where c is the number of column treatments, r the number of row treatments, n the number of observations in each cell, x_ijk the individual observation, the mean of the cell corresponding to ith row and jth column (cell mean)

and MSE (mean square) =

where SSE is the sum of squares of errors and rc (n – 1) the degrees of freedom.

SST (total sum of squares) =

where c is the number of column treatments, r the number of row treatments, n the number of observations in each cell, x_ijk the individual observation, the grand mean.

and MST (mean square) =

where SST is the total sum of squares and N – 1 the degrees of freedom (total number of observa- tions – 1).

14.6.3 Applying the F-Test Statistic

As discussed, the total sum of squares consists of four parts: SST (total sum of squares) = SSC (sum of squares between columns) + SSR (sum of squares between rows) + SSI (sum of squares interaction) + SSE (sum of squares of errors)

In case of two-wayANOVA, the F value can be obtained as below:

F-test statistic in two-way ANOVA

where MSC is the mean square column and MSE the mean square error

with c – 1, degrees of freedom for numerator and

rc (n – 1) degrees of freedom for denominator.

where MSR is the mean square row and MSE the mean square error

with r – 1, degrees of freedom for numerator and

rc (n – 1) degrees of freedom for denominator.

where MSI is the mean square interaction and MSE the mean square error

with (r – 1)(c – 1), degrees of freedom for numerator and

rc (n – 1), degrees of freedom for denominator.

For a given level of significance α, rules for acceptance or rejection of null hypothesis are as below:

For a given level of significance α, rules for acceptance or rejection of null hypothesis

Reject H₀, if F_calculated > F_critical, otherwise, do not reject H₀.

14.6.4 ANOVA Summary Table for Two-Way ANOVA

The result of ANOVA for a factorial design is usually presented in an ANOVA table (shown in Table 14.12).The entries in the table consist of SSC (sum of squares between columns), SSR (sum of squares between rows), SSI (sum of squares interaction), SSE (sum of squares of errors), SST (total sum of squares); corresponding degrees of freedom (c – 1); (r – 1); (c – 1)(r – 1); rc (n – 1) and (N – 1); MSC (mean square column); MSR (mean square row); MSI (mean square interaction) and MSE (mean square error); F values in terms of F_treatment; F_block , and F_interaction. Software programs such as MS Excel, Minitab, and SPSS, calculate p-value test in the ANOVA table, which allows a researcher to make inferences directly without taking help from the critical values of the F distribution.

TABLE 14.12 ANOVA Summary table for two-way ANOVA

Example 14.3

Chhattisgarh Steel and Iron Mills is a leading steel rod manufacturing company of Chhattisgarh. The company produces 8-metre long steel rods, which are used in the construction of buildings. The company has four machines which manufacture steel rods in three shifts. The company’s quality control officer wants to test whether there is any difference in the average length of the iron rods by shifts or by machines. Data given in Table 14.13 is organized by machines and shifts obtained through a random sampling process. Employ a two-way analysis of variance and determine whether there are any significant differences in effects. Take α = 0.05.

TABLE 14.13Length of the iron rod in different shifts and produced by different machines

 

Soultion

The seven steps of hypothesis testing can be performed as below:

Step 1: Set null and alternative hypotheses

The null and alternative hypotheses can be stated as below:

Row effect: H₀: All the row means are equal.

H₁: All the row means are not equal.

Column effect: H₀: All the column means are equal.

H₁: All the column means are not equal.

Interaction effect: H₀: Interaction effects are zero.

H₁: Interaction effect is not zero (present).

Step 2: Determine the appropriate statistical test

F-test statistic in two-way ANOVA

where MSC is the mean square column and MSE the mean square error

with c – 1, degrees of freedom for numerator and

rc (n – 1) degrees of freedom for denominator.

where MSR is the mean square row and MSE the mean square error

with r – 1, degrees of freedom for numerator and

rc (n – 1) degrees of freedom for denominator.

where MSI is the mean square interaction and MSE is the mean square error. with (r – 1)(c – 1), degrees of freedom for numerator and

rc (n – 1) degrees of freedom for denominator.

Step 3: Set the level of significance

Let α = 0.05.

Step 4: Set the decision rule

For a given level of significance α, the rules for acceptance or rejection of the null hypothesis are

Reject H₀ if F_calculated > F_critical, otherwise, do not reject H₀.

For treatments, degrees of freedom = (c – 1) = (3 – 1) = 2

For blocks, degrees of freedom = ( r – 1) = (4 – 1) = 3

For interaction, degrees of freedom = (c – 1)(r – 1) = 2 = 6

For error, degrees of freedom rc(n – 1) = 4 = 24

Step 5: Collect the sample data

The sample data is given in Table 14.14:

TABLE 14.14 Sample data for Example 14.3 and computation of different means

Grand mean = 7.99055

Step 6: Analyse the data

SSR (sum of squares between rows) =

= 1.02077

SSC (sum of squares between columns) =

= 0.00376

SSI (sum of squares interaction) =

= 0.02527

SSE (sum of squares errors) =

= 0.0568

SST (total sum of squares) =

= 1.106589

MSR (mean square)

MSC (mean square)

MSI (mean square)

MSE (mean square)

 

Table 14.15 presents the ANOVA summary table for Example 14.3.

TABLE 14.15 ANOVA Summary table for Example 14.3

Step 7: Arrive at a statistical conclusion and business implication

At 95% confidence level, the critical value obtained from the table is F_{0.05, 2, 24} = 3.40, F_{0.05, 3, 24} = 3.01 and F_{0.05, 6, 24} = 2.51.

The calculated value of F for columns is 0.79. This is less than the tabular value (3.40) and falls in the acceptance region. Hence, the null hypothesis is accepted and the alternative hypothesis is rejected.

The calculated value of F for rows is 143.77. This is greater than the tabular value (3.01) and falls in the rejection region. Hence, the null hypothesis is rejected and alternative hypothesis is accepted.

The calculated value of F for interaction is 1.78. This is less than the tabular value (2.51) and falls in the acceptance region. Hence, the null hypothesis is accepted and the alternative hypothesis is rejected.

The result indicates that there is a significant difference in the steel rods produced by different machines. The results also indicate that the difference in the length of the steel rods produced in three shifts are not significant and the differences obtained (as exhibited from the sample result) are due to chance. Additionally, interaction between machines and shifts is also not significant and differences (as exhibited from the sample result) are due to chance. Therefore, the management must focus on the machines to ensure that the steel rods produced by all the machines are uniform.

Self-Practice Problems

14C1. Perform two-way ANOVA on the data arranged in the form of a two-way factorial design below:

14C2. Perform two-way ANOVA analysis on the data arranged in form of a two-way factorial design as below:

14C3. A company organized a training programme for three categories of officers: sales managers, zonal managers, and regional managers. The company also considered the education level of the employees. Based on their qualifications, officers were also divided into three categories: graduate, post graduates, and doctorates. The company wants to ascertain the effectiveness of the training programme on employees across designation and educational levels. The scores obtained from randomly selected employees across different categories are given below:

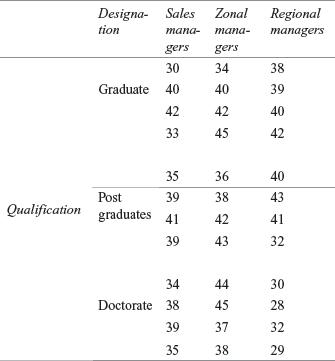
Employ a two-way analysis of variance and determine whether there are significant differences in effects. Take α = 0.05

SUMMARY

An experimental design is the logical construction of the experiment to test hypotheses in which researcher either controls or manipulates one or more variables. Analysis of variance or ANOVA is a technique of testing a hypothesis about the significant difference in several population means. In analysis of variance (one-way classification), the total variation in the sample data can be divided into two components, namely variance between the samples and variance within the samples. Variance between the samples is attributed to the difference among the sample means. This variance is due to some assignable causes. One-way ANOVA is used to analyse the data from completely randomized designs.

Like completely randomized design, randomized block design also focuses on one independent variable of interest (treatment variable). Additionally, in randomized block design, we also include one more variable referred to as “blocking variable.” This blocking variable is used to control the confounding variable. Confounding variables are not being controlled by the researcher but can have an impact on the outcome of the treatment being studied. In case of a randomized block design, variation within the samples can be partitioned in two parts: unwanted variance attributed to difference between block means (block sum of square) (SSR); variance attributed to random error sum of squares errors) (SSE).

In some real-life situations, a researcher has to explore two or more treatments simultaneously. This type of experimental design is referred to as factorial design. In a factorial design, two or more treatment variables are studied simultaneously. Factorial design provides a platform to analyse both the treatment variables simultaneously at the same time in one ­experimental design. In a factorial design, a researcher can control the effect of multiple treatment variables. In addition, factorial design provides an opportunity to study the interaction effect of two treatment variables. The total sum of squares consists of four parts: SSC (sum of squares between columns), SSR (sum of squares between rows), SSI (sum of squares interaction), and SSE (sum of squares of errors).

Key terms

Analysis of variance, 333

Classification variable, 332

Completely randomized design, 333

Dependent variable, 333

Experimental design, 332

Experimental units, 333

Factor, 333

Factorial design, 333

Independent variable, 332

Randomized block design, 333

Treatment variable, 332

note

1. www.tatamotors.com/our_world/profile.php, accessed August 2008.

Discussion Questions

1. Explain the concept of using experimental designs for hypothesis testing.
2. Define the following terms:
   • Independent variable
   • Treatment variable
   • Classification variable
   • Experimental units
   • Dependent variable
3. What do you understand by ANOVA? What are the major assumptions of ANOVA?
4. What is the concept of completely randomized design and under what circumstances can we use completely randomized design for hypothesis testing?
5. Explain the procedure for calculating SSC (sum of squares between columns) and SSE (sum of squares within samples) in a completely randomized design.
6. Discuss the concept of randomized block design? Under what circumstances can we adopt randomized block design? Explain your answer in light of blocking variable and confounding variable.
7. Explain the procedure of calculating SSC (sum of squares between columns), SSR(sum of squares between rows), and SSE (sum of squares of errors) in a randomized block design.
8. Explain the difference between completely randomized design and randomized block design.
9. What do you understand by factorial design? Explain the concept of interaction in a factorial design.
10. Explain the procedure of calculating SSC (sum of squares between columns), SSR (sum of squares between rows), SSI (sum of squares interaction), and SSE (sum of squares of errors).

Numerical Problems

1. There are four cement companies A, B, C, and D in ­Chhattisgarh. Company “A” is facing a problem of high employee turnover. The personnel manager of this company believes that the low job satisfaction levels of employees may be one of the reasons for the high employee turnover. He has decided to compare the job satisfaction levels of the employees of his plant with those of the three other plants. He has used a questionnaire with 10 questions on a Likert rating scale of 1 to 5. The maximum scores that can be obtained is 50 and the minimum score is 10. The personnel manager has taken a random sample of 10 employees from each of the organizations with the help of a professional research organization. The scores obtained by the employees are given in the table below.

Use one-way ANOVA to analyse the significant difference in the job satisfaction scores. Take 99% as the confidence level.

2. A company has launched a new brand of soap Brand 1 in the market. Three different brands of three different companies already exist in the market. The company wants to know the consumer preference for these four brands. The company has randomly selected 10 consumers of each of the four brands and used a 1 to 4 rating scale, with 1 being the minimum and 4 being the maximum. The scores obtained are tabulated below:

Use one-way ANOVA to analyse the significant difference in the consumer preference scores. Take 95% as the confidence level.

3. A consumer durable company located at New Delhi has launched a new advertisement campaign for a product. The company wants to estimate the impact of this campaign on different classes of consumers. For the same purpose, the company has divided consumer groups into three classes based on occupations. These are service class, business class, and consultants. For measuring the impact of the advertisement campaign, the company has used a questionnaire, which consists of 10 questions, on a 1 to 7 rating scale with 1 being minimum and 7 being maximum. The company has randomly selected 8 subjects (respondents) from each of the classes. So, a subject can score a minimum of 10 and maximum of 70. The scores obtained from the three classes of consumers are given below:

Use one-way ANOVA to determine the significant difference in the mean scores obtained by different consumers. Assume α = 0.05

4. A company has employed five different machines with five different operators working on it turn-by-turn. The table given below shows the number of units produced on randomly selected days by five machines with the concerned operator working on it:

Use a randomized block design analysis to examine:

(1) Whether the operators significantly differ in ­performance?

(2) Whether there is a significant difference between the machines?

Take 90% as the confidence level.

5. A woolen threads manufacturer recently purchased three new machines. The company wants to measure the performance of these three machines at three different temperatures (in terms of unit production per day). The following table depicts the performance of the three machines at three different temperatures on randomly selected days:

Use a randomized block design analysis to examine:

(1) Whether the machines are significantly different in terms of performance?

(2) Whether there is a significant difference between the three different temperatures in terms of production?

Take 95% as the confidence level.

6. A company wants to ascertain the month wise ­productivity of its salesmen. The sales volume generated by five randomly selected salesmen in the first five months is given in the following table:

Use a randomized block design analysis to examine:

(1) Whether the salesmen are significantly different in terms of performance?

(2) Whether there is a significant difference between five months in terms of production?

Take 90% as the confidence level.

7. A company wants to measure the satisfaction level of consumers for a particular product. For this purpose, the company has selected respondents belonging to four age groups and asked a simple question, “Are you satisfied with this product?” Respondents were also classified into four regions. On the basis of four different age groups and regions, 48 customers were randomly selected. The company used a nine-point rating scale. The data given below represents the responses of the consumers:

Employ two-way ANOVA to determine whether there are any significant differences in effects. Take α = 0.05.

9. A water purifier company wants to launch a new model of its popular product. The company has divided its potential customers into three categories, “middle class,” “upper-middle class,” and “upper class.” Potential customers are further divided among three states of India, “Gujarat,” “Delhi,” and “Punjab.” For determining the purchase intention of the potential randomly selected consumers, the company has used a simple question, “Does this new product appeal to you?” The questionnaire is administered to 36 randomly selected customers from different classes and states. The company has used a five-point rating scale. The table given below depicts the responses of these randomly selected potential consumers:

Employ a two-way ANOVA and determine whether there are any significant differences in effects. Take α = 0.01.

10. Black Pearl is a leading tyre manufacturing company in Pune. In the last 10 years, the company has achieved success in terms of branding, profitability, and market share. As a downside, the management has realized that the highly competitive and stressful environment has reduced its employee morale. For boosting employee morale, the company has opted for three methods: motivational speeches, meditation, and holidays with pay. The company researchers measure the success of the three-point programme after taking random samples from three departments, marketing, finance, and production. The researchers have used a questionnaire (10 questions) on a five-point rating scale. So, the maximum score can be 50 and minimum score can be 10. The scores obtained from 36 randomly selected employees are as shown in the given table:

Employ a two-way ANOVA and determine whether there are any significant differences in effects. Take α = 0.05.

Case Study

Case 14: Tyre Industry in India: A History of Over 75 Years

Introduction

The Indian government has been placing high emphasis on the building of infrastructure in the country. This has given a tremendous fillip to the development of road infrastructure and transport. After liberalization, there has been a remarkable increase in the numbers of vehicles on Indian roads. As a direct result of this, a heavy demand for tyres has been forecast in the near future. Indian tyre manufacturing companies have started re-engineering their businesses and are looking at strategic tie-ups worldwide to meet this demand.¹ Table 14.01 shows the market segmentation for different categories of tyres.

TABLE 14.01 Market segmentation for different categories of tyres

Major Players in the Market

MRF Ltd, Apollo Tyres Ltd, Ceat Ltd, JK Industries Ltd, GoodYear, Dunlop, etc. are some of the major players in the market. MRF Ltd is the leader in the market. The company is involved in the manufacturing, distribution, and the sales of tyres, tubes, and flaps for various vehicles. CEAT, established in 1958, is a part of the PRG group. CEAT is also a key player in the market and offers a wide range of tyres for almost all segments like heavy-duty trucks and buses, light commercial vehicles, earthmovers, forklifts, tractors, trailers, cars, motorcycles, and scooters, etc.

Apollo Tyres Ltd is also a dominant player in the truck, bus, and light commercial vehicle categories. In January 2008, the company announced an investment of 12,000 million to set up a passenger car radial plant in Hungary to cater to the needs of the European and the North American market. It acquired Dunlop Tyre International along with its subsidiaries in Zimbabwe and the UK in April 2006¹. Apollo Tyres CMD, Mr Onkar Singh Kanwar, optimistically stated, “We believe that alliances offer the power of many companies working together for the benefit of the customer. This ultimately is for the greater good of the market and the individual companies.”²

TABLE 14.02Net sales of four leading tyre manufacturers for six randomly selected quarters

JK Industries Ltd is the pioneer in launching radial tyres in India. Radial tyres cost 30% more but are technologically superior to conventional tyres. JK Tyres is the key player in the four-wheeler tyre market. In 1922, Goodyear tyre and rubber company Akron, Ohio, USA, entered the Indian market. Goodyear India has pioneered the introduction of tubeless radial tyres in the passenger car segment. Dunlop India Ltd is also a leading player in the market.

Worry Over Chinese Imports

Between April and December 2006, 550,000 trucks and bus tyres were imported from China when compared to just over 3 lakh units during the financial year 2005–2006. The increase in imports of low-priced tyres from China has become a sore point for Indian tyre manufacturers. Indian manufacturers are relying on the superior quality of Indian tyres to fight this battle. Mr Arun K. Bajoria, President, JK Tyre and Industries Ltd argued, “The quality of an Indian tyre and Chinese tyre cannot be compared. Indian tyres are exported to around 80 countries around the world and we have no complaints from anywhere on the quality.”³

With world class products under its stable, Indian tyre companies are getting ready to cater to an estimated demand of 22 million units of car and jeep tyres; 57 million units of two-wheelers tyres; 6.5 million units of LCV tyres; 17 million units of HCV tyres by 2014–2015.⁴

Let us assume that a researcher wants to compare the mean net sales of four leading companies Apollo Tyres Ltd, Ceat Ltd, JK Industries Ltd and MRF Ltd. The researcher is unable to access the complete net sales data of these companies and has taken a random sample of net sales for six quarters of the four companies taken for the study. Table 14.02 shows the net sales (in million rupees) of four leading tyre manufacturers in randomly selected quarters. Apply techniques presented in this chapter to find out whether:

1. The companies significantly differ in performance?
2. There is a significant difference between the quarterly sales of these companies?

NOTES

1. Prowess (V. 3.1), Centre for Monitoring Indian Economy Pvt. Ltd, Mumbai, accessed August 2008, reproduced with permission.
2. www.tribuneindia.com/2003/200330901/biz.htm, acce­ssed August 2008.
3. www.thehindubusinessline.com/2007/07/20/stories/ 2007072050461400.htm, accessed August 2008.
4. www.indiastat.com, accessed August 2008, reproduced with permission.