Chapter 16

Correlation and Simple Linear Regression Analysis

Learning Objectives

Upon completion of this chapter, you will be able to:

• Use the simple linear regression equation
• Understand the concept of measures of variation, coefficient of determination, and standard error of the estimate
• Understand and use residual analysis for testing the assumptions of regression
• Measure autocorrelation by using the Durbin–Watson statistic
• Understand statistical inference about slope, correlation coefficient of the regression model, and testing the overall model

16.1 Measures of association

Measures of association are statistics for measuring the strength of a relationship between two variables. This chapter focuses on only one measure of association, that is, correlation for two numerical variables.

16.1.1 Correlation

Correlation measures the degree of association between two variables. For example, a marketing manager may be interested in knowing the degree of relationship between two variables: sales and advertisement. In this section, we focus on one method of determining correlation between two variables: Karl Pearson’s coefficient of correlation.

16.1.2 Karl Pearson’s Coefficient of Correlation

Karl Pearson’s coefficient of correlation is a quantitative measure of the degree of relationship between two variables. Suppose these variables are x and y, then Karl Pearson’s coefficient of correlation is defined as

The coefficient of correlation lies in between +1 and –1. Figure 16.1 explains how coefficient of correlation measures the extent of relationship between two variables. Figure 16.2 exhibits five examples of correlation coefficient.

Figure 16.1 Interpretation of correlation coefficient

Figure 16.2 Five examples of correlation coefficient

Example 16.1

Table 16.2 shows the sales revenue and advertisement expenses of a company for the past 10 months. Find the coefficient of correlation between sales and advertisement.

Table 16.2 Sales and advertisement for 10 months

Solution As discussed, the correlation coefficient between sales and advertisement can be obtained by applying Karl Pearson’s coefficient of correlation formula as shown in Table 16.3.

Table 16.3 Calculation of correlation coefficient between sales and advertisement

Hence, correlation coefficient between sales and advertisement is –0.51. This indicates that sales and advertisement are negatively correlated to the extent of –0.51. We can conclude that an increase in the expenditure on advertisements will not result in an increase in sales.

16.2 INTRODUCTION TO SIMPLE LINEAR REGRESSION

Regression analysis is the process of developing a statistical model, which is used to predict the value of a dependent variable by at least one independent variable. In simple linear regression analysis, there are two types of variables. The variable whose value is influenced or is to be predicted is called the dependent variable and the variable which influences the value or is used for prediction is called the independent variable. In regression analysis, the independent variable is also known as regressor or predictor or explanatory while the dependent variable is also known as regressed or explained variable. In a simple linear regression analysis, only a straight line relationship between two variables is examined. In fact, simple linear regression analysis is focused on developing a regression model by which the value of the dependent variable can be predicted with the help of the independent variable, based on the linear relationship between these two. This does not mean that the value of a dependent variable cannot be predicted with the help of a group of independent variables. This concept will be discussed in the next chapter (Chapter 17). In the next chapter, we will focus on non-linear relationship and regression models with more than one independent variable. Determining the impact of advertisement on sales is an example of simple linear regression. Determining the impact of other variables such as personal selling, distribution support and advertisement on sales in an example of multiple regression.

16.3 DETERMINING THE EQUATION OF A REGRESSION LINE

Simple linear regression is based on the slope–intercept equation of a line. This equation is given as

y = ax + b

where a is the slope of the line and b the y intercept of the line.

The straight line regression model with respect to population parameters β₀ and β₁ can be given as

y = β₀ + β₁x

where β₀ is the population y intercept which represents the average value of the dependent variable when x = 0 and β₁ the slope of the regression line which indicates expected change in the value of y for per unit change in the value of x.

In case of specific dependent variable y_i

y_i = β₀ + β₁x_i + e_i

where β₀ is the population y intercept, β₁ the slope of the regression line, y_i the value of the dependent variable for ith value, x_i the value of the independent variable for ith value, and e_i the random error in y for observation i (e is the Greek letter epsilon).

e is the error of the regression line in fitting the points of the regression equation. If a point is on the regression line, the corresponding value of e is equal to zero. If the point is not on the regression line, the value of e measures the error. This concept leads to two models in regression; deterministic model and probabilistic model.

A deterministic model is given as

y = β₀ + β₁x

A probabilistic model is given as

y = β₀ + β₁x + e

It can be noticed that in the deterministic model, all the points are assumed to be

on the regression line and hence, in all the cases random error e is equal to zero. Probabilistic model includes an error term which allows the value of y to vary for any given value of x. Figure 16.3 presents error in simple regression.

Figure 16.3 Error in simple regression

In order to predict the value of y, a researcher has to calculate the value of β_o and β₁. In this process, difficulty occurs in terms of observing the entire population. This difficulty can be handled by taking a sample data and ultimately developing a sample regression model. This sample regression model can be used to make predictions about population parameters. So, β₀ and β₁ (population parameters) are estimated on the basis of the sample statistics b₀ and b₁. Thus, the simple regression equation (based on samples) is used to estimate the linear regression model.

The equation of the simple regression line is given as

where b₀ is the sample y intercept which represent the average value of the dependent variable when x =b₁ the slope of the sample regression line, which indicates expected change in the value of y for per unit change in the value of x.

For determining the equation of the simple regression line, values of b₀ (sample y intercept) and b₁ (slope of the sample regression line) must be determined. Once b₀ and b₁ are determined, a researcher can plot a straight line and the comparison of this straight line with the original data can be performed very easily. The main focus of simple regression analysis is on finding the straight line that fits the data best. In other words, we need to minimize the difference between the actual values ( y_i) and the regressed values . This difference between the actual values ( y_i) and the regressed values is referred to as residual (e). In order to minimize this difference, a mathematical technique “least-squares method” developed by Carl Friedrich Gauss is applied. The sample data are used in the least squares method to determine the values of b₀ and b₁ that minimizes the sum of squared differences be

tween the actual values ( y_i) and the regressed values

where y_i is the actual value of y for observation i and the regressed (predicted) value of y for observation i.

An equation for computing the slope of a regression line is given below:

Slope of a regression line

where

and

The sample y intercept of the regression line is given as

It has already been discussed that in the estimation process through a simple linear regression, unknown population parameters, β₀ and β₁, are estimated by sample statistics b₀ and b₁. Figure 16.4 exhibits the summary of the estimation process for simple linear regression.

Figure 16.4 Summary of the estimation process for simple linear regression.

Example 16.2

A cable wire company has spent heavily on advertisements. The sales and advertisement expenses (in thousand rupees) for the 12 randomly selected months are given in Table 16.4. Develop a regression model to predict the impact of advertisement on sales.

Table 16.4 Sales and advertisement expenses (in thousand rupees) of a cable wire company

Solution The first step is to determine whether the relationship between two variables is linear. For doing this, a scatter plot, drawn by any of the statistical software programs (MS Excel, Minitab, or SPSS) can be used. Figure 16.5 is the scatter plot produced using Minitab.

Figure 16.5 Scatter plot between sales and advertisement produced using Minitab

Scatter plot (Figure 16.5) exhibits the linear relationship between sales and advertisement. After confirming the linear relationship between the two variables, further steps for developing a linear regression model can be adopted. For computing the regression coefficient, b₀ and b₁, the values of Σx, Σy, Σx², and Σxy must be determined. Sales is a dependent variable and advertisement is an independent variable.

Computation of Σx, Σy, Σx2, and Σxy for Example 16.2

= 19.0704

Equation of the simple regression line

This result indicates that for each unit increase in x (advertisement), y (sales) is predicted to increase by 19.07 units. b₀ (Sample y intercept) indicates the value of y when x = 0. It indicates that when there is no expenditure on advertisement, sales is predicted to decrease by 852.08 thousand rupees.

16.4 USING MS EXCEL FOR SIMPLE LINEAR REGRESSION

The first step is to select Data from the menu bar. Then select Data Analysis from this menu bar. The Data Analysis dialog box will appear on the screen as shown in Figure 16.6. From the Data Analysis dialog box, select Regression and click OK (Figure 16.6). The Regression dialog box will appear on the screen (Figure 16.7). Place independent variable in Input X Range and place dependent variable in Input Y range. Place appropriate confidence level in the Confidence Level box. In the Residuals box, check Residuals, Residual Plots, Standardized Residuals, and Line Fit Plot. From Normal Probability, select Normal Probability Plots and click OK (Figure 16.7). The MS Excel output (partial) as shown in (Figure 16.8) will appear on the screen.

Figure 16.6 MS Excel Data Analysis dialog box

Figure 16.7 MS Excel Regression dialog box

Figure 16.8 MS Excel output (partial) for Example 16.2

16.5 USING MINITAB FOR SIMPLE LINEAR REGRESSION

Select Stat from the menu bar. From the pull-down menu select Regression. Another pull-down menu will appear on the screen. Select Regression (linear) as the first option from this pull down menu.

The Regression dialog box will appear on the screen (Figure 16.9). Place dependent variable in the Response box and independent variable in the Predictors box. Minitab has the ability to open various dimensions of regression. From the Regression dialog box, click Graph, Options, Result, and Storage. The Regression-Graphs dialog box (Figure 16.10), the Regression-Options dialog box (Figure 16.11), the Regression-Results dialog box (Figure 16.12), and the Regression-Storage dialog box (Figure 16.13) will appear on the screen. The required output range can be selected from these dialog boxes. After selecting required options from each of the four dialog boxes, click OK. The Regression dialog box will reappear on the screen. Click OK. The partial regression output produced using Minitab will appear on the screen as shown in Figure 16.14.

Figure 16.9 Minitab Regression dialog box

Figure 16.10 Minitab Regression-Graphs dialog box

Figure 16.11 Minitab Regression-Options dialog box

Figure 16.12 Minitab Regression-Results dialog box

Figure 16.13 Minitab Regression-Storage dialog box

Figure 16.14 Minitab output (partial) for Example 16.2

16.6 USING SPSS FOR SIMPLE LINEAR REGRESSION

Select Analyze from the menu bar. Select Regression from the pull-down menu. Another pull-down menu will appear on the screen. Select Linear from this menu.

The Linear Regression dialog box will appear on the screen (Figure 16.15). Place dependent variable in the Dependent box and independent variable in the Independent(s) box. Like Minitab, SPSS also has the ability to open various dimensions of regression. From the Regression dialog box, click Statistics, Plots, Options, and Save. The Linear Regression: Statistics dialog box (Figure 16.16), the Linear Regression: Plots dialog box (Figure 16.17), the Linear Regression: Options dialog box (Figure 16.18), and the Linear Regression: Save dialog box (Figure 16.19) will appear on the screen. The required output range can be selected from these dialog boxes. After selecting required options from each of the four dialog boxes, click OK. The Linear Regression dialog box will reappear on the screen. Click OK. The regression output (partial) produced using SPSS will appear on the screen as shown in Figure 16.20.

Figure 16.15 SPSS Linear Regression dialog box

Figure 16.16 SPSS Linear Regression: Statistics dialog box

Figure 16.17 SPSS Linear Regression: Plots dialog box

Figure 16.18 SPSS Linear Regression; Options dialog box

Figure 16.19 SPSS Linear Regression: Save dialog box

Figure 16.20 SPSS output (partial) for Example 16.2

Self-Practice Problems

16A1. Taking x as the independent variable and y as the dependent variable from the following data, determine the line of regression. Let a = 0.05.

16A2. Taking x as the independent variable and y as the dependent variable from the following data, construct a scatter plot and determine the line of regression. Let a = 0.05.

16A3. A company believes that the number of salespersons employed is a good predictor of sales. The following table exhibits sales (in thousand rupees) and number of salespersons employed for different years.

Develop a simple regression model to predict sales based on the number of salespersons employed.

16A4. Cadbury India Ltd, incorporated in 1948, is the wholly owned Indian subsidiary of the UK-based Cadbury Schweppes Plc., which is a global confectionary and beverages company. Cadbury India Ltd operates in India in the segments of chocolates, sugar confectionary, and food drinks.² The following table provides data relating to the profit after tax and advertisement of Cadbury India Ltd from 1989–1990 to 2006–2007.

Develop a simple regression line to predict the profit after tax from advertisement.

16.7 Measures of Variation

While developing a regression model to predict the dependent variable with the help of the independent variable, we need to focus on a few measures of variations. Total variation (SST) can be partitioned into two parts: variation which can be attributed to the relationship between x and y and unexplained variation. The first part of variation, which can be attributed to the relationship between x and y is referred to as explained variation or regression sum of squares (SSR). The second part of variation, which is unexplained can be attributed to factors other than the relationship between x and y, and is referred to as error sum of squares (SSE). So, in a simple linear regression model, total variation, that is, the total sum of squares is given as:

Total sum of squares (SST) = Regression sum of squares (SSR) + Error sum of squares (SSE)

Total sum of squares (SST) is the sum of squared differences between each observed value (y_i) and the average value of y.

Total sum of squares = (SST) =

Regression sum of squares (SSR) is the sum of squared differences between regressed (predicted) values and the average value of y.

Regression sum of squares = (SSR) =

Error sum of squares (SSE) is the sum of squared differences between each observed value (y_i) and regressed (predicted) value of y.

Error sum of squares = (SSE) =

Figure 16.21 exhibits the measures of variation in simple linear regression. It can be seen easily that Total sum of squares (SST) = regression sum of squares (SSR) = 125,197.4582 (SSR) +13,769.20842 (SSE)

Figure 16.21 Measures of variation in simple linear regression

Figure 16.22 is the ANOVA table produced using MS Excel exhibiting values of SST, SSR and SSE and other values for Example 16.2. The same ANOVA table as shown in Figure 16.22 can be obtained using Minitab and SPSS. Figures 16.14 and 16.20 exhibit this ANOVA table containing SST, SSR, and SSE values obtained from Minitab and SPSS, respectively.

Figure 16.22 Values of SST, SSR and SSE for Example 16.2 produced using MS Excel

16.7.1 Coefficient of Determination

Coefficient of determination is a very commonly used measure of fit for regression models and is denoted by r². The utility of SST, SSR, and SSE is limited in terms of direct interpretation. The ratio of regression sum of squares (SSR) to total sum of squares (SST) leads to a very important result, which is referred to as coefficient of determination. In a regression model, the coefficient of determination measures the proportion of variation in y that can be attributed to the independent variable x. The values of coefficient of determination range from 0 to 1. Coefficient of determination can be defined as

In Example 16.2, coefficient of determination r² can be calculated as

As discussed, the coefficient of determination leads to an important interpretation of the regression model. In Example 16.2, r² is calculated as 0.9009. This indicates that 90.09% of the variation in sales can be explained by the independent variable, that is, advertisement. This result also explains that 9.91% of the variation in sales is explained by factors other than advertisement.

Figures 16.23, 16.24, and 16.25, are the partial regression outputs from MS Excel, Minitab, and SPSS respectively, exhibiting coefficient of determination and other important results.

Figure 16.23 Partial regression output from MS Excel showing coefficient of determination and other important results

Figure 16.24 Partial regression output from Minitab showing coefficient of determination and other important results

Figure 16.25 Partial regression output from SPSS showing coefficient of determination and other important results

16.7.2 Standard Error of the Estimate

It has already been

discussed that sample data are used in the least squares method to determine the values of b₀ and b₁ that minimize the sum of squared differences between the actual values (y_i) and the regressed values . Variability in actual values (y_i) and the regressed values is measured in terms of residuals. A residual is the difference between the actual values (y_i) and the regressed values x. The residual around the regression line is given as

Residual (e_i) = actual values (y_i) – regressed values

Variation of the dots around the regression line represents the degree of

relationship between two variables x and y. Though the least squares method results in a regression line that fits the data best, all the observed data points do not fall exactly on the regression line. There is an obvious variation of the observed data points around the regression line. So, there is a need to develop a statistic which can measure the differences between the actual values (y_i) and the regressed values . Standard error fulfils this need. Standard error measures the amount by which the regressed values are away from the actual values (y_i). This is the same as the concept of standard deviation that we developed in Chapter 11. Standard deviation measures the deviation of data around the arithmetic mean; similarly, standard error can be understood as the standard deviation around the regression line. Standard error of the estimate can be defined as

Standard error of the estimate

where y_i is the actual value of y, for observation i and the regressed (predicted) value of y, for observation i.

In the above formula, the numerator is the error sum of squares and the denominator is degrees of freedom determined by subtracting the number of parameters, β₀ and β₁, that is, 2 from sample size n. Hence, the degrees of freedom is n – 2. In Example 16.2, the sample size is 12 and there are two parameters. Therefore, the degrees of freedom can be computed as 12 – 2 = 10. A large standard error indicates a large amount of variation or scatter around the regression line and a small standard error indicates small amount of variation or scatter around the regression line. A standard error equal to zero indicates that all the observed data points fall exactly on the regression line.

For Example 16.2, standard error of the estimate can be computed as

Figures 16.23, 16.24, and 16.25 exhibit the computation of standard error from MS Excel, Minitab, and SPSS, respectively. Figure 16.26 is the scatter plot exhibiting actual values and the regression line for Example 16.2.

Figure 16.26 Scatter plot exhibiting actual values and the regression line for Example 16.2

Table 16.5 indicates the predicted (regressed) values and residuals for Example 16.2.

Table 16.5 Predicted (regressed) values and residuals for Example 16.2

Figures 16.27, 16.28, and 16.29 exhibit the computation of predicted values (fits) and residuals, and are the part of the regression outputs obtained from MS Excel, Minitab, and SPSS, respectively.

Figure 16.27 MS Excel output (partial) exhibiting the computation of predicted values, residuals, and standardized residuals for Example 16.2

Figure 16.28 Minitab output (partial) exhibiting the computation of residuals and predicted values (fits) for Example 16.2

Figure 16.29 SPSS output (partial) exhibiting the computation of predicted values (fits) and residuals for Example 16.2

It is important to note that the sum of residuals is approximately zero. Ignoring some rounding off errors, the sum of residuals is always equal to zero. The logic behind this is very simple. Residuals are geometrically the vertical distance from the regression line to the data point. The regression equation used to solve for the intercept and slope place the line of regression in the middle of all the data points. So, the vertical distance from the line to data points cancel each other and lead to a sum that is approximat

ely equal to zero. Figure 16.26 is the scatter plot with residuals (distance between actual values and predicted values) for Example 16.2. This figure clearly exhibits that that the line of regression is geometrically in the middle of all the data points. This also exhibits that the residuals with (+) sign fall above the regression line and residuals with (–) sign fall below the regression line. Table 16.5 clearly exhibits that the sum of residuals is approximately equal to zero. Residuals are also used to find out outliers in the data set. This can be done by examining the scatter plot. Outliers can produce residuals with large magnitudes. These outliers may be due to misreported or miscoded data. These outliers sometimes pull the regression line towards them and hence put undue influence on the regression line. A researcher after identifying the origin of the outlier can decide whether the outlier should be retained in the regression equation or regression line should be computed without it.

Self-Practice Problems

16B1. Compute the value of r² and standard error for Problem 15A1. Discuss the meaning of the value of r² and standard error in developing a regression model.

16B2. Compute the value of r² and standard error for Problem 15A2. Discuss the meaning of the value of r² and standard error in developing a regression model.

16B3. Nestle India Ltd, incorporated in 1959, is one of the largest dairy product companies in India. The company has a broad product portfolio comprising of milk products, beverages, prepared dishes, cooking aids, chocolate, and confectionary. The following table shows the net sales (in million rupees) and salaries and wages (in million rupees) of the company for different quarters.

Develop a simple regression line to predict net sales from salaries and wages. Discuss the meaning of the value of r² and standard error in developing a regression model.

16.8 STATISTICAL INFERENCE ABOUT SLOPE, CORRELATION COEFFICIENT OF THE REGRESSION MODEL, AND TESTING THE OVERALL MODEL

If there is no serious violation of the assumption of linear regression and residual analysis has confirmed that the straight line regression model is appropriate, an inference about the linear relationship between variables can be obtained on the basis of sample results.

16.8.1 t Test for the Slope of the Regression Line

After verifying the assumptions of linear regression, a researcher has to determine whether a significant linear relationship exists between the independent variable x and the dependent variable y. This is determined by performing a hypothesis test to check whether the population slope (β₁) is zero. The hypotheses for the test can be stated as below:

H₀: β₁ = 0 (There is no linear relationship)

H₁: β₁ ≠ 0 (There is a linear relationship)

Any negative or positive value of the slope will lead to the rejection of the null hypothesis and acceptance of the alternative hypothesis (as the above hypothesis test is two-tailed). A negative value of the slope indicates the inverse relationship between the independent variable x and the dependent variable y. This means that larger values of the independent variable x are related to smaller values of the dependent variable y and vice versa. In order to test the significant positive relationship between the two variables, the null and alternative hypotheses can be stated as below:

H₀: β₁ = 0 (There is no linear relationship)

H₁: β₁ > 0 (There is a positive relationship)

To test the significant negative relationship between the two variables, the null and alternative hypotheses can be stated as below:

H₀: β₁ = 0 (There is no linear relationship)

H₁: β₁ > 0 (There is a negative relationship)

The test statistic t can be defined as below:

where

The test statistic t follows a t distribution with n – 2 degrees of freedom and β₁ as the hypothesized population slope.

On the basis of above formula, the t statistic for Example 16.2 can be computed as

where

Figures 16.30(A), 16.30(B), and 16.30(C) show the computation of the t statistic using MS Excel, Minitab, and SPSS, respectively.

Figure 16.30(a) Computation of the t statistic for Example 16.2 using MS Excel

Figure 16.30(b) Computation of t statistic for Example 16.2 using Minitab

Figure 16.30(c) Computation of the t statistic for Example 16.2 using SPSS

Using the p value from the above outputs, the null hypothesis is rejected and the alternative hypothesis is accepted at 5% level of significance. In light of the positive value of b₁ and p value = 0.000, it can be concluded that a significant positive linear relationship exists between the independent variable x and the dependent variable y.

16.8.2 Testing the Overall Model

The F test is used to determine the significance of overall regression model in regression analysis. More specifically, in case of a multiple regression model, the F test determines that at least one of the regression coefficients is different from zero. In case of simple regression, where there is only one predictor the F test for overall significance tests the same phenomenon as the t-statistic test in simple regression. The F statistic can be defined as the ratio of regression mean square (MSR) and error mean square (MSE).

F statistic for testing the slope

where = 1).

The F statistic follows the F distribution with degrees of freedom k and n – k – 1.

Figures 16.31(A), 16.31(B), and 16.31(C) illustrate the computation of F statistic using MS Excel, Minitab, and SPSS, respectively. On the basis of the p value obtained from the outputs, it can be concluded that expenses on advertisement is significantly (at 5% level of significance) related to sales. If we compare the p value obtained from Figures 16.30 and 16.31, we find that the p values are the same in both the cases.

Figure 16.31(b) Computation of F statistic for Example 16.2 using Minitab

Figure 16.31(a) Computation of the F statistic from MS Excel for Example 16.2

Figure 16.31(b) Computation of F statistic for Example 16.2 using Minitab

Figure 16.31(c) Computation of F statistic for Example 16.2 using SPSS

16.8.3 Estimate of Confidence Interval for the Population Slope (β₁)

Estimate of confidence interval for the population slope (β₁) provides an alternative approach to test the linear relationship between the independent variable x and the dependent variable y. This can be done by determining whether the hypothesized value of β₁ (β₁ = 0) is within the interval or outside the interval. For understanding the concept, we will take Example 16.2 again. Confidence interval for the population slope (β₁) is defined as

Estimate of confidence interval for the population slope (β₁)

From the outputs given in Figures 16.8, 16.14, and 16.20, the following values can be obtained

b₁ = 19.0704 n = 12, and S_b = 1.9999

From the table, for = n – 2 = 10, the value of t is 2.2281. By substituting all these values in the formula of confidence interval estimate for the population slope, we get

b₁ = 19.0704 = 19.0704 ± (4.4559)

So, the upper limit is 23.5263 (19.0704 + 4.4559) and the lower limit is 14.6145 (19.0704 – 4.4559).

So, population slope β₁ is estimated with 95% confidence to be in the interval of 14.6145 and 23.5263. Hence,

14.6145 ≤ β₁ ≤ 23.5263

The upper limit as well as the lower limit is greater than 0 and population slope lies in between these two limits. So, it can be concluded with 95% confidence that there exists a significant linear relationship between advertisement and sales. If the interval would have included 0, the inference would have been different. In this situation, the existence of a significant linear relationship between the two variables could not have been concluded. This confidence interval also indicates that for each thousand rupee increase in the advertisement expenditure, sales will increase by at least 14,614.50 but less than 23,526.30 (with 95% confidence).

16.8.4 Statistical Inference about Correlation Coefficient of the Regression Model

From Figures 16.8, 16.14, and 16.20, it can be seen that the value of correlation coeffic

ient is a part of the output. Correlation coefficient (r) measures the strength of the relationship between two variables. Correlation coefficient (r) specifies whether there is a statistically significant relationship between two variables. The t test can be applied to check this. The population correlation coefficient (r) can be hypothesized as equal to zero. In this case, the null and the alternative hypotheses can be stated as follows:

H₀: r = 0

H₁: r ≠ 0

In order to test the significant relationship between two numerical variables statistically, the t statistic can be defined as

The t statistic for testing the statistical significant correlation coefficient

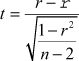
where , if b₁ ≥ 0

, if b₁ < 0

The t statistic follows the t distribution with n – 2 degrees of freedom. From Figures 16.8, 16.14, and 16.20, the following values can be obtained:

r = 0.9491 and b₁ = 19.0704

By substituting these values in the above formula, we get

From the table, for = n – 2 = 10, the value of t is 2.2281. The calculated value of t is 9.53. The calculated value of t (= 9.53) = 2.2281). Hence, the null hypothesis is rejected and the alternative hypothesis is accepted. So, it can be concluded there is a significant relationship between two variables. It is important to note that the value of t is the same as calculated in Figures 16.8, 16.14, and 16.20.

The statistical significance of correlation coefficient can be directly inferred using Minitab and SPSS.

SUMMARY

Regression analysis is the process of developing a statistical model which is used to predict the value of a dependent variable by at least one independent variable. In simple linear regression analysis, there are two types of variables. The variable whose value is influenced or is to be predicted is called dependent variable and the variable which influences the value or is used for prediction is called independent variable. Simple linear regression is based on the slope–intercept equation of a line. In regression analysis, sample regression model can be used to make predictions about population parameters. So, β₀ and β₁ (population parameters) are estimated on the basis of sample statistics b₀ and b₁. For this purpose, least squares method is used. Least-squares method use the sample data to determine the values of b₀ and b₁ that minimizes the sum of squared differences between actual values (y_i) and the regressed values . Once line of regression is developed, by substituting the required variable values and values of regression coefficient, regressed values, or predicted values can be obtained.

While developing a regression model to predict the dependent variable with the help of independent variable, we need to focus on a few measures of variations. Total variation (SST) can be partitioned in two parts: variation which can be attributed to the relationship between x and y and unexplained variation. First part of variation which can be attributed to the relationship between x and y is referred to as explained variation or regression sum of squares (SSR). The second part of the variation, which is unexplained can be attributed to factors other than the relationship between x and y is referred to as error sum of squares (SSE). Coefficient of determination is also a very important phenomenon in regression analysis. Coefficient of determination measures the proportion of variation in y that can be attributed to independent variable x. A residual is the difference between actual values (y_i) and the regressed values and is used to examine the magnitude of the errors produced by the regression model. In addition, residual analysis can be used to verify the assumptions of regression analysis. These assumptions are (1) linearity of the regression model (2) constant error variance (homoscedasticity) (3) independence of error (4) normality of error.

After verifying the assumptions of linear regression, a researcher determines whether a significant linear relationship between independent variable x and dependent variable y exists. This can be done by performing a hypothesis test to check whether the population slope (β₁) is zero or not. The t test is applied for this purpose. A significant p value for the t statistic establishes the linear relationship between the independent variable x and the dependent variable y. In regression analysis, the F test is used to determine the significance of the overall regression model. More specifically, in case of a multiple regression model, the F test determines that at least one of the regression coefficients is different from zero. In case of simple regression, where predictor is only one, the F test for overall significance tests the same phenomenon as the t-statistic test in simple regression. Apart from coefficient of determination (r²), regression analysis also provides the correlation coefficient (r), which measures the strength of the relationship between two variables. Correlation coefficient (r) specifies whether there is a significant relationship between two variables. Again t statistic is used to determine the significant relationship between two variables.

Key terms

Coefficient of determination (r²), 400

Correlation, 384

Correlation coefficient (r), 409

Dependent variable, 386

Error sum of squares (SSE), 399

Independent variable, 386

Least-squares method, 388

Measures of association, 384

Regression sum of squares (SSR), 399

Residual, 388

Standard error, 402

Total sum of squares (SST), 399

NOTES

1. www.tatasteel.com/Company/profile.asp,accessed September 2008.
2. Prowess (V. 3.1), Centre for Monitoring Indian Economy Pvt. Ltd, Mumbai, accessed September 2008, reproduced with permission.

Discussion questions

1. What is the conceptual framework of simple linear regression and how can we use it for marketing decision making?
2. Regression analysis is an important tool for forecasting. Explain this statement.
3. Explain the concept of regression sum of squares (SSR) and error sum of squares (SSE) in a regression model.
4. Explain the concept of coefficient of determination and standard error of the estimate in a regression model.
5. How can we use the t test for determining the statistical significance of the slope of the regression line?
6. How can we test the significance of the overall regression model?
7. How can we use correlation coefficient (r) for determining the statistical significance of the relationship between two variables in a regression model?

Numerical problems

1. A large supermarket has adopted a new strategy to increase its sales. It has adopted a few consumer friendly policies and is using video clips of 15 minutes to propagate the new policies. The following table provides data about the number of video clips shown in a randomly selected day and the sales turnover of the supermarket in the corresponding day.

(1) Develop a regression model to predict sales from the number of video clips shown.

(2) Calculate the coefficient of determination and interpret it.

(3) Calculate the standard error of the estimate.

2. The HR manager of a multinational company wants to determine the relationship between experience and income of employees. The following data are collected from 14 randomly selected employees.

(1) Develop a regression model to predict income based on the years of experience.

(2) Calculate the coefficient of determination and interpret it.

(3) Calculate the standard error of the estimate.

(4) Predict the income of an employee who has 22 years of experience.

3. A dealer of a motorcycle company believes that there is a positive relationship between the number of salespeople employed and the increase in the sales of bikes. Data for 14 randomly selected weeks are given in the following table.

(1) Develop a regression model to predict sales from the number of salespeople employed.

(2) Calculate the coefficient of determination and interpret it.

(3) Calculate the standard error of the estimate.

(4) Predict sales when number of salespeople employed are 100.

4. For Problem 3, estimate the following:

(1) t Test for the slope of the regression line

(2) Testing the overall model

(3) Statistical inference about the correlation coefficient of the regression model

5. For Problem 2, estimate the following:

(1) t Test for the slope of the regression line

(2) Testing the overall model

(3) Statistical inference about the correlation coefficient of the regression model

6. The municipal corporation of a newly formed capital city is planning to launch a new water supply scheme for the city. For this, the Municipal Corporation has considered past data on water consumption in 16 randomly selected weeks of the previous summer and the average temperature in the corresponding week. On the basis of the data, the corporation wants to estimate the water requirement for the current year. Data are given as below:

(1) Develop a regression model to predict water consumption from the temperature of the corresponding week.

(2) Calculate the coefficient of determination and interpret it.

(3) Calculate the standard error of the estimate.

(4) Predict the water consumption when temperature is 47 °F.

(5) t Test for the slope of the regression line

(6) Test the overall model

(7) Statistical inference about correlation coefficient of the regression model

7. A company is concerned about the high rates of absenteeism among its employees. It organized a training programme to boost the morale of its employees. The following table gives the number of days that sixteen randomly selected employees have received training, and the number of days they have availed leave.

(1) Develop a regression model to predict leaves based on training days.

(2) Calculate the coefficient of determination and state its interpretation.

(3) Calculate the standard error of the estimate.

(4) Predict the leaves when training days are 25.

(5) t Test for the slope of the regression line

(6) Test the overall model

(7) Statistical inference about the correlation coefficient of the regression model

(8) Calculate Durbin–Watson statistic and interpret it.

Case study

Case 16: Boom in the Indian Cement Industry: ACC’s Role

Introduction

The Indian cement industry was delicensed in 1991. After China, India is the second largest producer of cement. The estimated demand for cement is 265 million metric tonnes by 2114–2115.¹ The Indian cement industry saw a growth of 11.6% in 2006. The financial year 2007 also witnessed a muted growth of 7.1%. In order to meet the increasing demand, several manufacturers have embarked on significant capacity expansion plans.²

ACC—A Pioneer in the Indian Cement Industry

Associated Cement Companies Ltd (ACC) came into existence in 1936, after the merger of 10 companies belonging to four important business groups: Tatas, Khataus, Killick Nixon, and F E Dinshaw. The Tata group was associated with ACC since its inception. It sold 14.45% of its share to Gujarat Ambuja Cements Ltd between 1999 and 2000. After this strategic alliance, Gujarat Ambuja Cements Ltd became the largest single stakeholder in ACC. In 2005, ACC entered into a strategic relationship with the Holcim group of Switzerland, a world leader in cement as well as a large supplier of concrete, aggregates, and certain construction related services. These global strategic alliances have strengthened the company.³

ACC is India’s foremost manufacturer of cement and concrete. The company has a wide range of operations with 14 modern cement factories, more than 30 ready mix concrete plants, 20 sales offices, and several zonal offices. ACC’s research and development facility has a unique track record of innovative research, product development, and specialized consultancy services. ACC’s brand name is synonymous with cement and it enjoys a high level of equity in the Indian market.⁴

The Impact of Cartelization

Cartelization is one of the major problems in the cement industry. Cartelization takes place when dominant players of the industry join together to control prices and limit competition. In the Indian market, manufacturers have been known to enter into agreements to artificially limit the supply of cement so that the price remains high. When markets are not sufficiently regulated, large companies may be tempted to collude instead of competing with each other. For example, in May 2006, the Competition Council of Romania imposed a combined fine of 27 million euros on France’s Lafarge, Switzerland’s Holcim, and Germany’s Carpatcement for being involved in the cement cartel in the Romanian market. These three companies share 98% of Romanian cement capacity.⁴ The government should take appropriate action to check acts of cartelization.

Escalating input and fuel costs have forced manufacturers to tap new sources of supply and increase the quest for alternative fuels and raw materials. The cement industry is faced with the challenge of optimizing the utilization of scare basic raw materials and fossil fuels while simultaneously protecting the environment and maintaining emission levels within acceptable limits. It is vital for the cement industry to achieve high levels of energy utilization efficiencies and to sustain them continuously.² Table 16.01 exhibits sales turnover and advertisement expenses of ACC from 1995 to 2007.

Table 16.01 Sales turnover and advertisement expenditure of ACC from 1995–2007

1. 1. Develop an appropriate regression model to predict sales from advertisement.
2. 2. Calculate the coefficient of determination and state its interpretation.
3. 3. Calculate the standard error of the estimate.
4. 4. Predict the sales when advertisement is 500 million.
5. 5. Test the significance of the overall model.

NOTES

1. www.indiastat.com, accessed September 2008, reproduced with permission.
2. Prowess (V. 3.1), Centre for Monitoring Indian Economy Pvt. Ltd, accessed September 2008, reproduced with permission.
3. www.acclimited.com/newsite/heritage.asp, accessed September 2008.
4. www.acclimited.com/newsite/corprofile.asp, accessed September 2008.
5. ww.businesstoday.org/index.php?option=com_content &task=viewed&id=370&Itemi, accessed September 2008.