APPENDIX A

Review of Set Theory

The purpose for reviewing set theory is to provide a mathematical structure for organizing methods for counting and grouping objects. Set theory may be used to define the probabilities of possible outcomes of experiments. There are two common methods for defining a set. The first method, known as the roster method, is to list the elements of a set. Synonyms for sets include class, aggregate, and collection. We will denote sets by capital letters, A, B, C, etc. The elements or objects of a set will be indicated by lowercase letters, such as a, b, c, etc. If a is an element (or object or member or point) of A, then we denote this as a ∈ A. If a is not an element of A, this is denoted as a ∉ A. A second way of defining a set is called the property method, which describes some property held by all elements of the set, but is not held by objects that do not belong to the set.

Definition A.1: A set A is said to be a subset of another set B if all elements of A are also in B. In which case we write A ⊆ B. With this definition, it is possible that the two sets are equal (i.e., they have all the same elements) in which case A ⊆ B and at the same time B ⊆ A. If on the other hand, A is a subset of B and there are some elements of B which are not in A, then we say that A is a proper subset of B and we write A ⊂ B.

Definition A.2: The universal set, S, is the set of all objects under consideration in a given problem, while the empty set, Ø, is the set that contains no elements.

Definition A.3: The complement of a set A, written , is the set of all elements in S which are not in A. For two sets A and B which satisfy A ⊂ B, the difference set, written B − A, is the set of elements in B which are not in A.

Note that for any set A, Ø ⊆ A ⊆ S and A ⊆ A. Also, if A ⊆ B and B ⊆ C, then A ⊆ C. Finally, we also note the relationship = Ø.

Definition A.4: For any two sets A and B, the union of the two sets, A ∪ B, is the set of all elements which are contained in either A or B and the intersection of the two sets, A ∩ B, is the set of all elements which are contained in both A and B. In the algebra of sets, the union operation plays the role of addition and so sometimes the notation A + B is used while the intersection operation plays the role of multiplication and hence the alternative notations A • B or AB are common.

Some of the concepts just presented are illustrated using a Venn diagram in Figure A.1. The set A is contained within the thick solid line, the set B within the dashed line, the set A + B is the set of points inside either line and the set AB is the set of points inside both. The set A − AB is the set of points inside the solid line but not inside the dashed line, while the set B − AB is the set of points inside the dashed line but not inside the solid line. The set is the set of all points outside of both lines.

Definition A.5: Two sets A and B are said to be mutually exclusive, or disjoint, if and only if they have no common elements, in which case A ∩ B = Ø. A collection of sets A₁, A₂, …, A_n are said to be exhaustive if each element in the universal set is contained in at least one of the sets in the collection. For exhaustive sets, A₁ ∪ A₂ ∪ … ∪ A_n = S.

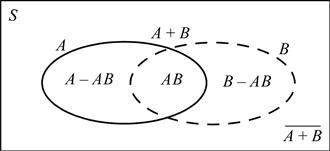
Figure A.1 A Venn diagram illustrating some of the concepts of sets.

The following laws are consequences of the definitions we have just introduced. The reader should verify these laws to gain familiarity with the algebra of sets.

De Morgan’s laws can be stated in the following way. To find the complement of an expression replace each set by its complement and interchange additions with multiplications and multiplications with additions.