APPENDIX B

Review of Linear Algebra

The study of probability and random processes draws heavily upon concepts and results from elementary linear algebra. In the text, we assume that the reader has a working knowledge of undergraduate level linear algebra. The aim of this appendix is to provide a review for those who need to brush up on these concepts. This review is not intended to be an exhaustive treatment of the topic, but rather is a summary of selected concepts that are used within the text.

Definition B.1: A matrix is a two-dimensional array of numbers. We say that a matrix has size m × n if the array has m rows and n columns. If the matrix has only one row, then we refer to it as a row vector while if there is only one column it is a column vector. A matrix with one row and one column is called a scalar. The elements of a matrix, B, are written as b_i,j , where the first subscript represents the row number and the second subscript gives the column number.

Definition B.2: The transpose of a matrix is obtained by exchanging the row and column number of each element. That is, if matrix B has elements b_i,j , then the element in the ith row and j th column of B^T is b_j,i . Hence if a matrix has size m × n, then its transpose has size n χ m. Also, the transpose of a column vector is a row vector and the transpose of a row vector is a column vector. A matrix B is said to be symmetric if B^T = B.

Definition B.3: The Hermitian transpose (or just Hermitian) of a matrix B is written B^H and is formed by taking the complex conjugate of the transpose. That is, if matrix B has elements b_i,j , then the element in the ith row and jth column of B^H is b^* _{j, i} . A matrix B is said to be Hermitian symmetric if B^H = B. Sometimes such a matrix is simply called a Hermitian matrix.

Definition B.4: Addition and multiplication of matrices is defined as follows. If two matrices A and B have the same size (same number of rows and columns), then their sum is defined as C = A + B where c_{i, j} = a_ij+ b_{i, j} . That is, matrix addition is done on an element-by-element basis. If the two matrices do not have the same dimensions, they cannot be added. If A has size m × k and B has size k × n, then their product C = AB will be an m × n matrix whose elements are given by

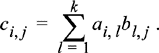(B.1)

In order for the matrix product AB to be defined, the number of columns in A must equal the number of rows in B.

It is also common to define two different products involving vectors, the so-called scalar (or dot) product and the matrix (or cross) product. We have no occasion to use the cross product in this text and so we do not consider it here. For two column vectors a and b (both with the same number of elements), the dot product is defined as a • b = a^Hb where the standard definition of matrix multiplication as it applies to vectors is used. Two vectors are said to be orthogonal if their dot product is zero. Finally, the norm of a vector is .

With these definitions in place, the reader should be able to verify the following properties of matrix arithmetic:

In much of this text, many of the matrices we deal with are square. The following definition identifies some characteristics which can be applied to square matrices.

Definition B.5: A matrix B is diagonal if its elements satisfy b_{i, j} = 0 for all i ≥ j. A matrix is upper triangular if b_{i, j} = 0 for all i > j and lower triangular if b_i,j = 0 for all i ≤ j. Note that a diagonal matrix is simultaneously upper and lower triangular. Finally, a matrix is an m × m identity matrix if it is a diagonal matrix whose diagonal entries are all equal to one. The letter I is reserved to represent an identity matrix.

An identity matrix has the form

(B.2)

Sometimes we use a subscript to indicate the dimensions of the identity matrix. For example, I _m×m would represent an identity matrix with m rows and columns. Note that the identity matrix is the identity with respect to matrix multiplication. That is, for any m × n matrix B, I _{m × m} B = BI _{n × n} = B. The identity with respect to matrix addition would be a matrix of all zeros.

Definition B.6: The inverse of a square matrix B, written B⁻¹ (if it exists), is a matrix which satisfies BB^{− 1} = B⁻¹ B = I. If the matrix B is not square, then it may have a left inverse which satisfies B⁻¹ B = I and a different right inverse which satisfies BB^{− 1} = I. In fact, for non-square matrices, the left inverse and right inverse will not have the same dimensions.

The inverse of a square matrix need not exist, but if it does, it is unique and the left and right inverses are identical. If the inverse of a matrix does not exist, then the matrix is said to be singular, while if the inverse exists, the matrix is non-singular or invertible.

The inverse of a matrix plays an important role in the solutions of simultaneous linear equations. Consider the following system of n linear equations in n unknowns, .

(B.3)

By defining A as the n × n matrix of coefficients whose elements are a_{i, j} and the column vectors x = (x_1, x_2, …, x _n )^T and b = (b₁, b₂, …, b_n )^T, this system of equations can be written in matrix form as

(B.4)

Multiplying both sides by the inverse of A leads us to the solution

(B.5)

Hence if the coefficient matrix is invertible, the system has a unique solution. On the other hand, if the coefficient matrix is singular, then A⁻¹ does not exist and the set of equations does not have a unique solution. This would be the case if some of the equations in (B.3) were linearly dependent (redundant), in which case the system would have more than one solution, or if some of the equations were inconsistent which would lead to no solution. In either case of redundant or inconsistent equations, the rows of the A matrix will be linearly dependent and the inverse will not exist. Conversely, if the rows of A are linearly independent, the matrix will be invertible.

A few properties of matrices that are related to the inverse are listed below:

A single quantity that is extremely useful in characterizing the invertibility of a matrix is its determinant. The determinant can be rather difficult to define in a simple manner, but it has many useful properties. We use a recursive definition which may seem rather cryptic, but is probably the simplest definition and is also consistent with how determinants are often calculated.

Definition B.7: Let B be an n × n matrix with elements b_{i, j.} Define B_{(i, j)} to be the (n − 1)×(n − 1) matrix obtained by removing the ith row and jth column from B. Then, the determinant of B is defined recursively according to

(B.6)

This recursion, together with the definition that for a 1× 1 matrix B = [B], det(B) = b, is sufficient to calculate the determinant of any n × n matrix.

To see how this works, consider a 2×2 matrix.

(B.7)

This was obtained using i = 1 in (B.6). We could have also used i = 2 and achieved the same result

(B.8)

For a general 3 × 3 matrix, the determinant works out to be

(B.9)

Probably the most important property of determinants is that if det (B) = 0 then the matrix B is singular and conversely if det(B) ≠ 0, then B is invertible. This, along with some other important properties, are listed below. We will not prove any of these properties in this review.

In addition to computing determinants of matrices, we will also find need throughout the text to compute eigenvalues and eigenvectors of square matrices.

Definition B.8: For a square matrix B, the scalar λ is an eigenvalue and the vector x is a corresponding eigenvector if

(B.10)

Note that the previous equation can be written in the slightly different form (B − λ I)x = 0. The eigenvector x will be non-zero only if the matrix B − λ I is singular. If it were non-singular, we could multiply both sides by its inverse to obtain the trivial solution x = 0. Hence, the eigenvalues of the matrix B must be solutions to the equation

(B.11)

This is the so-called characteristic equation for the matrix B. For an n × n matrix, B, the characteristic equation will be an n th order polynomial equation in λ and hence an n × n matrix will have n eigenvalues (although some of them may be repeated). Corresponding to each eigenvalue, λ_k , is an eigenvector, x _k . Note that the eigenvector is not unique since if x_k satisfies (B.10) then any multiple of x _k will also satisfy the same equation and hence will also be an eigenvector. In order to resolve this ambiguity, it is common to normalize the eigenvectors so that ||x||² = 1, but the vector is still an eigenvector even if it is not normalized. In the case of repeated eigenvalues, there may also be corresponding eigenvectors which differ by more than just a scale constant.

Before listing the important properties of eigenvalues and eigenvectors, it is necessary to include one more definition.

Definition B.9: A matrix B is positive definite if z^HBz > 0 for any vector z and it is negative definite if z^HBz ≤ 0 for all z. If z^HBz = 0, then the matrix is referred to as positive semi-definite and if z^HBz ≤ 0, the matrix is negative semi-definite.

With this definition in place, we now list the following properties of eigenvalues and eigenvectors.

In many of the applications encountered in this text, the matrices we are dealing with are Hermitian. These matrices possess further properties which are not necessarily shared by all matrices. These additional properties make Hermitian matrices particularly convenient to work with.