10

Exploiting the Register Access Delays Before Instruction Scheduling

Usual periodic scheduling problems deal with precedence constraints having non-negative latencies. This seems a natural way for modeling scheduling problems, since task or instruction delays are generally non-negative quantities. However, in some cases, we need to consider edge latencies that not only model instruction latencies, but also model other precedence constraints. For instance, in register optimization problems devoted to optimizing compilation, a generic machine or processor model can allow considering access delays into/from registers. Edge latencies may be then non-positive, leading to a difficult scheduling problem in the presence of resource constraints.

This chapter is related to the problem of periodic scheduling with register requirement optimization; its aim is to solve the practical problem of register optimization in optimizing compilation. We show that preconditioning a data dependence graph (DDG) to satisfy register constraints before periodic scheduling under resources constraints may create circuits with non-positive distances, resulting from the acceptance of non-positive edge latencies. As a compiler construction strategy, it is forbidden to allow the creation of circuits with non-positive distances during the compilation flow because such DDG circuits do not guarantee the existence of a valid instruction schedule under resource constraints. We study two solutions to avoid the creation of these problematic circuits. The first solution is reactive; it tolerates the creation of non-positive circuits in a first step, and if detected in a further check step, makes a backtrack to eliminate them. The second solution is proactive; it prevents the creation of non-positive circuits in the DDG during the register optimization process. It is based on shortest path equations that define a necessary and sufficient condition to free any DDG from these problematic circuits. Then we deduce a linear program accordingly. We have implemented our solutions and we present successful experimental results.

10.1. Introduction

In an optimizing compilation process for instruction-level parallelism, we may be faced with the opportunity of bounding the register pressure before instruction scheduling. A typical problem, which we solve in this chapter, arises for all strategies handling registers before instruction scheduling. Indeed, when we have a target processor with architecturally visible delays to access registers (such as in very long instruction word (VLIW), Digital Signal Processing (DSP), explicitly parallel instruction computing (EPIC) and transport triggered architectures (TTA)), the model of register requirement offers more opportunities to reduce the register pressure than in a regular sequential/ superscalar processor. Such architectures are also called non-unit-assumed-latencies (NUAL).

Unfortunately, the opportunities offered by NUAL architectures are not fully or optimally exploited in existing register allocators. Two main reasons are as follows:

This chapter studies the latter point, i.e. we show that minimizing the number of registers in a loop program may prohibit the compiler from generating a code. That is, in theory, if registers are optimized before instructions scheduling as done in some optimizing compilers, we may be faced with the problem of impossible instructions scheduling. This situation is not acceptable in optimizing compilation, because when a programer writes a correct code, the compiler must be able to generate a executable low-level code.

We follow a formal methodology to deal with the above problem. We use a graph theoretical framework to define the exact problem and to prove a necessary and sufficient condition for its existence. We provide solutions based on graphs and linear programming. This chapter demonstrates the following points:

While the problem of non-positive circuits may arise in theory for any register optimization method performing before periodic scheduling, this chapter shows how to avoid the problem in the schedule independent register allocation (SIRA) framework [TOU 04]. As far as we know, the SIRA framework is the only existing formal method that handles register constraints before periodic instruction scheduling with multiple register types and delayed access to registers.

Before continuing, readers must be familiar with our notations on DDG and periodic instruction scheduling (SIRA) defined in previous chapters. This chapter is organized as follows. We start with describing the problem in section 10.2: we explain the problem resulted if we insert non-positive edges inside DDG (which in turn create non-positive circuits). Section 10.3 studies a sufficient and necessary condition that defines a DDG without non-positive circuits. This mathematical characteristic is used to propose a linear program in section 10.4, which is the core of our proactive method. Section 10.5 summarizes our experimental results and draws comparisons between the efficiency of the reactive and the proactive methods.

10.2. Problem description of DDG circuits with non-positive distances

A circuit C is said to be lexicographic-positive if λ(C) > 0, while λ(C) is a notation for Σ_e∈Cλ(e). A DDG is said to be lexicographic-positive iff all its circuits are also lexicographic-positive. A DDG is said to be schedulable iff there exists a valid SWP, that is an SWP satisfying all its cyclic precedence constraints, not necessarily satisfying other constraints such as resources or registers. A DDG computed from a sequential program is always lexicographic-positive, it is an inherent characteristic of imperative sequential languages. When a DDG is lexicographic-positive, there is a guarantee that a schedule exists for it (at least the initial sequential schedule).

Since SIRA is applied before instruction scheduling (see section 9.3), it modifies the DDG under the condition that it remains schedulable. If the target architecture has unit-assumed-latencies (UAL) code semantics (sequential code), then the introduced edges by any SIRA method (such as SIRALINA) have unit-assumed latencies, and the DDG remains lexicographic-positive. If the target architecture has explicit architectural delays in accessing registers (NUAL code semantics), then the introduced edges by SIRA are of the form e′ = (k_u^t ,v) with latencies δ(e′) = –δ_ω,t(v). Such latencies are non-positive.

If an edge latency is non-positive, this does not create specific problems for cyclic scheduling in theory, unless the latency of a circuit is negative too. The following lemma proves that if δ(C) < 0, then the DDG may not be lexicographic-positive.

LEMMA 10.1.– [BRI 10] Let G be a schedulable loop DDG with SWP. Let C be an arbitrary circuit in G. Then the following implications are true:

1) δ(C) ≥ 0 ⇒ λ(C) > 0;

2) δ(C) ≤ 0 ⇒ λ(C) may be non-positive.

The previous lemma proves that inserting negative edges inside a DDG can generate circuits with λ(C) ≤ 0. So, what is the problem with such circuits? Indeed, the answer comes from the cyclic scheduling theory. Given a cyclic DDG, let C ⁺ be the set of circuits with λ(C) > 0, let C^– be the set of circuits with λ(C) < 0 and let C⁰ be the set of circuits with λ(C) = 0. Then the following inequality is true [KOR 11]:

In other words, the existence of circuits inside C^– imposes hard real-time constraints on the value of I I. Such constraints can be satisfied with cyclic scheduling if we consider only precedence constraints [KOR 11]. However, if we add resource constraints (as will be carried out during the subsequent instruction scheduling pass), then the DDG may not be schedulable. Simply, it may be possible that the conflicts on the resources do not allow us to have an I I lower than .

When a circuit C ∈ C⁰ exists, this means that there is a precedence relationship between the statements belonging to the same iteration: that is, the loop body is no longer an acyclic graph as in the initial DDG.

For the sake of brevity, we also say that a circuit in C⁰ C^– is a non-positive circuit. Some concrete examples demonstrating the possible existence of non-positive circuits are drawn in [BRI 10]. According to our experiments in [BRI 10], inserting non-positive edges inside a large sample of representative DDG produce non-positive circuits in 30.77% of loops in SPEC2000 C applications (respectively, 28.16%, 41.90% and 92.21% for SPEC 2006, MEDIABENCH and FFMPEG loops). Note that this problem of non-positive circuits is not related exclusively to SIRA, but it is related to any pass of register optimization performing on the DDG level before SWP. As shown in [TOU 02, BRI 10], if register requirement is minimized or bounded (with any optimal method) before instruction scheduling, it may create a non-positive circuit.

As a compiler construction strategy, we must guarantee that the schedulable DDG produced after applying SIRA is always lexicographic-positive. Otherwise, there is no guarantee that the subsequent SWP pass would find a solution under resource constraints, and the code generation may fail. This problem is studied and solved in the next section.

10.3. Necessary and sufficient condition to avoid non-positive circuits

As mentioned previously, we need to ensure that the associated DDG computed by any SIRA method is lexicographic-positive. We have also noted that if the processor has UAL semantics then it is guaranteed that any associated DDG found by SIRA is lexicographic-positive. This is because the UAL semantic is used to model sequential processors; all inserted anti-dependence edges have latency equal to 1. Since all the edges in the associated DDG have positive latencies, and since the associated DDG is schedulable by SWP (guaranteed by SIRA), the DDG is necessarily lexicographic- positive.

Hence, a naive strategy is to always consider UAL semantics, which defines the first sufficient condition to eliminate non-positive circuits. That is, we do not exploit the access delays to registers. This solution works in practice but the register requirement model is not optimal, since it does not exploit NUAL code semantics. Consequently, the computed register requirement is not well optimized.

A more clever, yet naive, way to ensure that any associated DDG computed by SIRA is lexicographic-positive is to have a reactive strategy. It tolerates the problem as follows:

Considering a UAL semantic for SIRA on a processor that has a NUAL semantic cannot hurt: it just possibly implies a loss of optimality in either II or in the register requirement. The above method is optimistic (reactive) in the sense that it considers that non-lexicographic DDGs are rare in practice. This is not true in theory of course, but maybe the practice would highlight that the proportion of the problems producing DDG that must be corrected is low. In this case, it is better in practice not to try to restrict SIRA, but to correct the solution afterwards if we detect the problem.

Thus, the question that naturally arises is the following: is it possible to devise a better method to ensure a priori that the associated DDG computed by SIRA is lexicographic-positive while exploiting the benefit of NUAL semantics? That is, we are willing to study a proactive strategy that prevents the problem. The following simple lemmas, deduced from [COR 01], are a basis for a necessary and sufficient condition to eliminate non-positive circuits. Their proof is easy due to shortest path equations.

LEMMA 10.2.– [TOU 13a] Let G = (V, E) be a directed graph and w : E → be a cost function. Then G has a circuit C of non-positive cost with respect to cost w if and only if G has a circuit of negative cost with respect to cost w′ defined by

LEMMA 10.3.– [TOU 13a] Let G = (V, E) be a directed graph and w : E → be a cost function.

Then G has a circuit C of negative cost (i.e. Σ_e∈C w(e) < 0 ) if and only if the constraints’ system S_G,w defined below is infeasible.

From lemmas 10.2 and 10.3, we deduce the following corollary, which defines a necessary and sufficient condition to eliminate non-positive circuits.

COROLLARY 10.1.– Let G = (V, E) be a directed graph and w : E → be a cost function.

Then G has a circuit C of non-positive cost with respect to cost w (i.e. Σ_e∈C w(e) ≤ 0) if and only if the system composed of the following constraints is infeasible.

where ∀_υ ∈ V, x_υ ∈ .

Now, any produced DDG by any register optimization method (hence, any SIRA method), must guarantee the above condition to eliminate non-positive circuits. In this chapter, we show how to combine the above condition with an efficient heuristic of SIRA that constructs a reuse graph (and hence the associated DDG accordingly), named SIRALINA. The next section studies this question.

10.4. Application to the SIRA framework

The problem that must be solved by SIRA is to construct a reuse graph. There are many heuristics and methods that may be used. SIRALINA [DES 11, TOU 11] is our most powerful method; we have already demonstrated that it is really an efficient heuristic for SIRA: it considers an initial DDG with multiple register types and produces an associated DDG to bound or to minimize the register requirement before SWP. SIRALINA is a two-step heuristic, with an algorithmic complexity equal to O(||V||³ log ||V||), where ||V|| is a notation for the cardinality of a set. It has been shown that SIRALINA, applied on a large set of benchmarks [DES 11, TOU 11], is fast and efficient in practice. So it has been connected to an industry quality compiler for embedded systems targeting VLIW ST231 processors. The next section briefly recalls SIRALINA; if the readers are familiar with our previous publication on the topic, they may skip the section. The following section shows how to eliminate non-positive circuits in the context of SIRALINA.

10.4.1. Recall on SIRALINA heuristic

Computing a valid reuse graph for a fixed-period II that minimizes Σ_{er∈E^reuse,t} μ^t(e_r) is NP-complete [TOU 04]. SIRALINA heuristic [DES 11, TOU 11] computes an approximate solution to this problem for all register types conjointly. In order to balance between the importance of each involved register type, we assume to have a weight ψ_t ∈ attributed to each type t ∈ . This weight may be set to 1 if all register types have the same importance.

SIRALINA is composed of two polynomial steps summarized as follows (here, the period II is fixed):

1) Step 1 (scheduling problem): determine minimal reuse distances for all pairs of values (i.e. compute, for each type t, a function );

2) Step 2 (linear assignment problem): determine a bijection E^reuse,t : V^R,i → V^R,t that minimizes for each t.

These two steps allow the construction of a reuse graph for a period II. Then G′ = (, ε) the associated DDG is constructed as explained previously: = V ∪ K and ε = E ∪ E^k ∪ E^μ. The two following sections detail each of the two above steps.

10.4.2. Step 1: the scheduling problem for a fixed II

The objective of the scheduling problem [DES 11, TOU 11] is to guarantee the existence of a SWP schedule for the associated DDG. The problem is formulated as an integer linear problem with a totally unimodular constraints matrix. In addition, it aims to determine minimal reuse distances for all pairs of values. The two next paragraphs define the integer linear program of the scheduling problem.

Integer variables of the linear problem

For any u ∈ , define a variable σ_u ∈ representing a scheduling date.

Linear program formulation

The scheduling problem is expressed as follows (section 9.4):

The constraints matrix of this integer linear program is an incidence matrix of the DDG G (with killing nodes); consequently, it is totally unimodular. Hence, it can be solved with a polynomial algorithm.

Let σ_u* and σ_kut * be the values of the variables of the optimal solution of the above scheduling problem. The minimal reuse distance function, denoted by , is then defined as follows for all pairs of values (u, v):

This minimal reuse distance constitutes the lower bound of the optimal values of the optimization problem solved by SIRALINA.

10.4.3. Step 2: the linear assignment problem

The objective of the linear assignment problem for a register type t is to find a bijection θ^t : V ^R,t → V ^R,t such that is minimal. It can be solved in polynomial time complexity with the so-called Hungarian algorithm [KUH 55]. Such an optimal bijection θ^t defines a set of reuse edges E^reuse,t as follows:

10.4.4. Eliminating non-positive circuits in SIRALINA

Thus, our idea is the following. Once an initial reuse graph has been computed by SIRALINA, the DDG associated with it may contain non-positive circuits. So, we have to eliminate these circuits. All the edge distances are fixed, except that we can increase the anti-dependence edge distances. That is, we can modify the values of to eliminate non-positive circuits. Modifying these reuse distances is a valid transformation as long as it does not violate the scheduling constraints. However, this transformation may require the use of more registers.

Indeed, observe that in the associated DDG, the added edges , where e_r = (u, v) is a reuse edge of type t, have a distance equal to λ(e) = (u, v), and that the distances of the other edges are entirely determined by the initial DDG and are not subject to changes. By modifying (u, v), the optimal solution to the linear assignment problem may be affected (step 2 of SIRALINA). In this case, we may choose to recompute the linear assignment. This defines an iterative process. We start by explaining this iterative process; then we describe how we modify the reuse distances.

Our iterative process is thus given by Algorithm 10.1. At each iteration i of the algorithm, it computes new reuse distances and new reuse edges , based on the previous reuse distances ) and previous reuse edges . This algorithm is parameterized by two functions:

– Linear Assignment(G, ) computes a bijection θ^t : V ^R,t × V ^R,t that minimizes . In other words, it solves the linear assignment problem and is typically implemented by the Hungarian algorithm, as done in the second step of SIRALINA. The result of this function is a new set of reuse edges

– Update Reuse Distances uses corollary 10.1 to compute new distance functions such that the associated DDG with respect to and is lexicographic-positive.

Our process stops after a certain number of iterations according to the time budget allowed for this optimization process. The body of the repeat-until loop is executed with a finite number of iterations, denoted n. The loop may be interrupted before reaching n iterations when a fixed point is reached, that is when the set of reuse edges stabilizes from one iteration to another . Since the body of algorithm loop is executed at least once, it is guaranteed that the associated DDG will be lexicographic-positive.

The following section explains our implementation of the function Update Reuse Distances.

10.4.5. Updating reuse distances

Our proactive method, named shortest path equations (SPE), is based on corollary 10.1. We deduce from it that the associated DDG is lexicographic-positive if and only if there exist || variables x_v ∈ for v ∈ such that

Recall that = V ∪ K where V is the set of vertices of the initial DDG and K is the set of all killing nodes. We are willing to modify each reuse distance by adding an integral increment γ^t to it. Our objective is still to minimize the register requirement, which means that we need to minimize the sum of γ^t . We thus define a linear problem as follows, which is our main contribution in this chapter.

For each vertex υ ∈ , we define a continuous variable x_υ. For each anti-dependence edge corresponding to the reuse edge e_r = (u, v), we define a variable γ^t(u, v), so that the distance of e is .

We seek to minimize the register requirement, which means minimizing , where ψ^t is a weight given to a register type, as defined in section 9.4. In order to guarantee that modifying the reuse distances is a valid transformation, we must ensure that the scheduling constraints are not violated. This means that the modified reuse distances must be greater than or equal to their minimal values: for any , where (u, v) is the solution of the scheduling problem (step 1 of SIRALINA), which are indeed the minimal valid values for the reuse distances. Since γ^t denotes integral values, we should write a mixed integer linear program. But such a solution is computationally expensive. So we decided to write a relaxed linear program in Figure 10.1, where γ^t variables are declared as continuous. Afterwards, we safely ceil these variables to obtain integer values. The linear program of Figure 10.1 contains O(|| + |ε|) variables and O(|ε|) linear equations. Once a solution is found for the linear program of Figure 10.1, we set the new distance of e = (k_u^t, v) ∈ E^μ,t as equal to .

Figure 10.1. Linear program based on shortest paths equations (SPE)

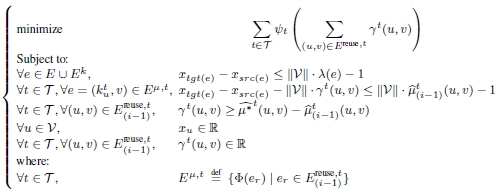
Hence, our implementation of Update Reuse Distances, is given by Algorithm 10.2.

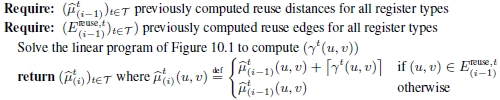
10.5. Experimental results on eliminating non-positive circuits

Our SPE method is integrated inside SIRAlib, available as an open source in [BRI 10]. Full experiments and public data are also exposed. A summary is provided in Appendix 4.

Our experiments declare the following conclusions:

10.6. Conclusion on non-positive circuit elimination

Preconditioning a DDG before SWP is a beneficial approach for reducing spill code and improving the performance of loops. Until now, schedule-sensitive register optimization was studied only for sequential and superscalar codes, with UAL code semantics.

When considering NUAL code semantics, the access to registers may be architecturally delayed. These delay accesses provide interesting compilation opportunities to save registers. These opportunities are exploited by the insertion of edges with non-positive latencies inside DDG.

Inserting edges with non-positive latencies inside DDG highlights two open questions. First, existing SWP and periodic scheduling methods do not handle these non-positive latencies yet. Second, a preconditioning step that optimizes registers before SWP may create circuits with non-positive distances.

DDG with non-positive circuits have the drawback of not being lexicographic-positive. This means that, when resource constraints are considered, the existence of a valid SWP is no longer guaranteed. This may cause the failure of the compilation process (no code is generated while the program is correct). Our experiments show that, if care is not taken, 30.77% of loops in SPEC2000 applications induce non-lexicographic positive circuits (respectively, 28.16%, 41.90% and 92.21% for SPEC 2006, MEDIABENCH and FFMPEG loops).

In order to avoid the situation of creating non-lexicographic positive DDG, we studied two strategies. First, we studied a reactive strategy that tolerates the problem: we start by optimizing the register pressure at the DDG level without special care; if a non-positive circuit is detected, then backtrack and consider a UAL code semantic instead of NUAL; this means that we degrade the model of the processor architecture by not exploiting the opportunities offered by delayed accesses to registers. Second, we designed a proactive strategy that prevents the problem. The proactive strategy is based on a necessary and sufficient condition that we prove. It is implemented as an iterative process that increases the reuse distances until a fixed point is observed (or until we reach a limit in terms of iterations).

Concerning the efficiency of the methods presented in this chapter, the reactive strategy seems to perform well in practice in a regular compilation process: when the number of architectural registers is fixed, register minimization is not necessary (just be sure to be below the architectural capacity). In this context, it is advised not to try preventing the problem of non-positive circuits, but to tolerate it in order to save compilation time. In other contexts of compilation, the number of architectural registers is not fixed. This is the case of reconfigurable circuits where the number of registers needed may be decided after code optimization and generation. It is also the case of architectures with frame registers such as EPIC IA64, where a minimal register requirement reduces the cost of function calls. Also, this may be used to keep as many registers as possible free in order to be used for other code optimization methods. In such situations, our proactive strategy is efficient in practice: the iterative register minimization saves better registers than in the reactive strategy, while the compilation time stays reasonable (although greater than the reactive strategy).

The SIRA framework allows us to make a formal relationship between the register requirement, the initiation interval and the unrolling degree. This formal relationship proved in theorem 9.1 gives us the opportunity to define an interesting problem of minimal loop unrolling using the set of remaining registers, as shown in the next chapter.

1 Due to Corollary 10.1, to be defined later.