4.1. The L²(Ω) space

The construction of complete function spaces is complex: as shown in the preceding examples, there is a contradiction between the assumptions of regularity used in order to verify that (u, u) = 0 ⇒ u = 0 and the assumption that Cauchy sequences have a limit in the space.

Such a difficulty has been illustrated, for instance, in example 3.5, with is continuous on Ω and (v, v) < ∞} and

In this example, we have shown a sequence {u_n: n ^*} such that u_n → u strongly, but . In order to overcome this difficulty, the method of completion has been introduced. Completion consists of generating a new vector space, referred to as L² (Ω) and formed by sets of Cauchy sequences on V (see [SOU 10]). L²(Ω) may be interpreted as follows: let V be the set of continuous square summable functions:

and

Then

is a Hilbert space (see [SOU 10]). Indeed, in this case,

In general, in order to alleviate the notation, the square brackets are not written and [v] is denoted by v. When using this simple notation, we must keep in mind that v (i.e. [v]) contains infinitely many elements, so that u(x) has no meaning. For instance, let us consider,

Then, ∀α ,u_α [0]. So, [u_α] = [0] and, u_α(x) = α, so that the class of the null function contains an infinite amount of elements and the value of has no meaning. When denoting [0] by 0, we must keep in mind that the values of 0 in a particular point vary. By these reasons, elements of L²(Ω) are sometimes referred to as generalized functions and completion implies a loss of information: point values are lost when passing to the complete space L²(Ω). In order to help the reader to keep in mind the difference between u and [u], we will use the notation:

Thus, index zero recalls that the elements on the scalar products are not standard functions, but classes, for which point values are not defined.

It must be noted that the construction of L²(Ω) may be carried using other spaces such as, for instance,

or

is often referred to as the set of test functions. A square summable function may be approximated by elements of these spaces, namely by using mollifiers introduced by Sobolev [SOB 38] and Friedrichs [FRI 44, FRI 53]. Moreover, these spaces are dense in L²(Ω).

In the following, this approach is generalized by Sobolev spaces, and a way to retrieve the notion of point values is given.

4.2. Weak derivatives

As observed above, passing from standard functions to generalized functions involves the loss of the notion of point values. This implies that the standard notion of derivative does not apply. Indeed, let Ω = (a,b), v L²(Ω): the quotient used to define the derivative at point x Ω reads as and has no meaning, since the values of v(x) and v(x + h) are undefined. Distribution theory proposed by Schwarz introduces a new concept, based on the integration by parts. Indeed, assume that v:Ω → is regular enough.

and, for a regular function φ such that φ(a) = φ(b) = 0,

so that v′ is characterized by the linear functional

This remark suggests the following definition:

DEFINITION 4.1.– Let Ω ⊂ ⁿ be a regular domain and u L²(Ω). The weak derivative is the linear functional defined by:

Weak derivatives are also referred to as distributional derivatives or generalized derivatives. We have:

THEOREM 4.1.– Let be the weak derivative ∂u/∂x_i, and verify:

Then, there exists a unique w_i L² (Ω) such that,

In this case, we say that w_i = ∂u/∂x_i.

PROOF–. Theorem 3.23 shows that ℓ_i extends to a linear continuous functional ℓ_i:L²(Ω) → . Therefore, the result is a consequence of Riesz (theorem 3.24).

COROLLARY 4.1.– Let ψ C¹(Ω)be such that both ψ and ∇ψ are square summable. Let u = [ψ] L²(Ω). Then ∂u/∂x_i = ∂ψ/∂x_i, for 1 ≤ i ≤ n, i.e. the weak and classical derivatives coincide.

PROOF.– We observe that:

Thus, Green’s formula:

yields:

so that, taking M = ||∂ψ/∂x_i||₀,

and the result follows from theorem 4.1.

REMARK 4.1.– Standard derivation rules apply to weak derivatives, under the assumption that each element is defined. For instance, if , then,

However, in derivatives of composite functions, change of variables have the same properties as classical derivatives, provided each element is defined.

EXAMPLE 4.1.– Let Ω = (−1, 1), u(x) = |x|. Let us show that u’(x) = sign(x). Indeed,

and we have (recall that φ(−1) = φ(1) = 0).

Thus,

EXAMPLE 4.2.– Let Ω = (−1, 1), u(x) = sign(x). Let us show that u’ = 2δ₀, with δ₀(φ) = φ(0) [Dirac’s delta – see Chapter 6]. Indeed,

and we have (recall that φ(−1) = φ(1) = 0).

In this case, there is no w L²(Ω) such that ℓ(v) = (w, v)₀, ∀v L²(Ω).

4.2.1. Second-order weak derivatives

We have, for Ω = (a,b), (thus, φ(a) = φ(b) = φ′(a) = φ′(b) = 0)

Then, we may define:

DEFINITION 4.2.– Let Ω ⊂ ⁿ be a regular domain and u L²(Ω). The weak derivative ∂²u/∂x_i ∂x_j is the linear functional defined by:

Analogous to theorem 4.1, we have:

THEOREM 4.2.– Let be the weak derivative ∂²u/∂x_i ∂x_j, and verify:

Then, there exists a unique w_ij L² (Ω) such that:

In this case, we say that w_ij = ∂²u/∂x_i ∂x_j.

The proof is analogous to these given in theorem 4.1.

EXAMPLE 4.3.– Let Ω = (−1, 1), u(x) = |x|. Let us show that u" = 2δ₀, with δ₀(φ) = φ(0) (Dirac’s delta, see Chapter 6). Indeed,

and we have (recall that φ′(−1) = φ′(1) = 0):

4.2.2. Gradient, divergence, Laplacian

Let Ω ⊂ ⁿ be a regular domain. Let u L²(Ω). The gradient of u, denoted by ∇u, is defined as , given by:

The Laplacian of u, denoted by Δu, is defined as , given by:

Let u = (u₁, …, u_n) [L²(Ω)]ⁿ. The divergence of u, denoted by div(u), is defined as , given by:

REMARK 4.2.– Classical results such as Green’s formulas or Stokes’ formula remain valid when using weak derivatives, under the assumption of each term has a meaning. For instance,

under the condition that each term (including products) is defined.

EXAMPLE 4.4.– Let , u(x) = ln r, . Let us show that Δu = 2πδ₀. Let , . Notice that , so that the weak and classical derivatives coincide on Ω_ε. Then, Green’s formula shows that:

Since on ∂Ω,

Using polar coordinates (r, θ) and taking into account that , ds = rdθ and that r = εon ∂Ω_ε, we have:

Since ε ln ε → 0 and

we have:

Thus,

EXAMPLE 4.5.– Let , , . Analogously to the preceding situation, we have . In this case, , and, using spherical coordinates (r, θ, ψ), we have ds = r² sinψdθdψ and that r = ε on ∂Ω_ε, so that

Thus

and

4.2.3. Higher-order weak derivatives

We have, for Ω = (a, b), φ ∈ (Ω),

Thus, we may define:

DEFINITION 4.3.– Let Ω ⊂ ⁿ be a regular domain and v ∈ L²(Ω). Let . The weak derivative is the linear functional defined by:

We have:

THEOREM 4.3.– Let be the weak derivative and verify:

Then, there exists a unique w_α ∈ L²(Ω) such that:

In this case, we say that

The proof is analogous to those given in theorem 4.1.

4.2.4. Matlab® determination of weak derivatives

Approximations of classical derivatives may be obtained by using the method derive defined in the class basis introduced in section 2.2.6. The evaluation of weak derivatives requests the use of scalar products, analogous to those defined in section 3.2.5. We present below a Matlab implementation using this last class. Recall that du = u′ verifies:

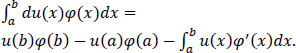
Let us consider a basis {φ_i:i ∈ } ⊂ S and

We have:

Thus, vector DU = (du₁, … , du_n) is the solution of a linear system A. DU = B, where .

Let us assume that the family is defined by a cell array basis such that basis{i} defines φ_i according to the standard defined in section 3.2.6: basis{i} is a structure having properties dim, dimx, component, where component is a cell array such that each element is a structure having as properties value and grad. u is assumed to be analogously defined. In this case, the weak derivative is evaluated as follows (Program 4.1):

EXAMPLE 4.6.– Let us consider the family φ_i(x) = xⁱ⁻¹ and u(x) = x⁴ The weak derivative is u′(x) = 4x³. We consider a = −1, b = 1. We generate the function by using the commands:

xlim.lower.x = a;
xlim.upper.x = b;
xlim.dim = 1;
u.dim = 1;
u.dimx = 1;
u.component = cell(u.dim,1);
u.component{1}.value = @(x) x^4;
ua = u.component{1}.value(a);
ub = u.component{1}.value(b);

Then, the commands

sp_space = @(u,v) scalar_product.sp0(u,v,xlim,'subprogram');
c = weak_derivative.coeffs(u,basis,sp_space,a,b,ua,ub,'subprogram');
du = weak_derivative.funcwd(c,basis);

generate the weak derivative by using the method “subprogram”. We may also generate a table containing the values of u as follows:

x = a:0.01:b;
p.x = x;
p.dim = 1;
U.dim = 1;
U.dimx = 1;
U.component = cell(U.dim,1);
U.component{1}.value = spam.partition(u.component{1}.value,p);

The commands

sp_space = @(u,v) scalar_product.sp0(u,v,p,'table');
ctab = weak_derivative.coeffs(U,tb,sp_space,a,b,ua,ub,'table');
dutab = weak_derivative.funcwd(ctab,basis);

generate the weak derivative by using the method “table”. The results are shown in Figure 4.1.

EXAMPLE 4.7.– Let us consider the family and u(x) = |x|. The weak derivative is u′(x) = sign(x). We consider a = −1, b = 1. The results are exhibited in Figure 4.2.

4.3. Sobolev spaces

As previously indicated, Serguei Lvovitch Sobolev was the Russian mathematician that introduced functional spaces fitting to variational methods, giving a complete mathematical framework. In his works, Sobolev formulated a theory of variational solutions and introduced Hilbert spaces involving derivatives [SOB 64], such as, for instance,

and

We may also consider Γ ⊂ ∂Ω such that meas(Γ) ≠ 0, i.e. Γ has a strictly positive length if its dimension is 1 and a strictly positive surface if its dimension is 2:

Sobolev spaces are generated by completion of particular spaces [SOB : 8]. For instance, by considering

and∇v are continuous on Ω and (v, v)₁<∞}

with the scalar product

the completion method generates H¹(Ω). Analogously, the completion

generates . Taking Γ = ∂Ω. generates .

The generic Sobolev space is denoted by:

and has a scalar product:

It is obtained by completion of a convenient space of continuous functions. We have H⁰(Ω) = L²(Ω).

Sobolev spaces are often invoked when solving partial differential equations. Note that they are formed by generalized functions.

One of the main properties of elements of Sobolev spaces are inequalities connecting an element and its weak derivatives. These inequalities are often referred to as Sobolev imbedding inequalities. For instance, we have Morrey’s inequality (see [EVA 10]).

THEOREM 4.4.– There exists ∈ such that

and Poincaré’s inequality (see [EVA 10]).

THEOREM 4.5.– Let Ω ⊂ ⁿ be open bounded, not empty. There exists ⊂ such that:

Sobolev spaces are separable (see, for instance, [LEB 96]).

4.3.1. Point values

The point value may have a meaning for elements from Sobolev spaces other than H⁰(Ω). For instance, let us consider Ω = (a,b) and u ∈ H¹(Ω)We have:

Let λ

We have:

so that,

This equality may be used to determine u(b). Let us define:

and ℓ_b:→ given by:

T_b is linear, so that ℓ_b is also linear. We have:

Moreover, there exists C such that,

Then, ℓ_b:→ is linear and continuous. From the Riesz theorem, there exists β such that ℓ_b (λ) = βλ. We define u(b) =β

The map H¹(Ω) ∋ u → β is the trace of u at b., denoted by γu.

It generalizes to higher dimension by considering Ω ⊂ ⁿ, u H¹(Ω), Γ ⊂ ∂Ω – in this case, we use the Green’s formula:

We may consider, for instance, ƒ L²(Γ) and

In this case,

and this equality may be used in order to define u on Γ, into an analogous way. Here,

Again, T_Γ is linear and

so that the existence of C such that:

yields that ℓ_Γ: L²(Γ) → is linear and continuous. In this case, from the Riesz theorem, there exists g L² (Γ) such that,

We define γu = g on Γ.

4.4. Variational equations involving elements of a functional space

Variational equations were introduced in Chapter 3 when considering orthogonal projections (equations [3.5], [3.7], [3.8]) and in Chapter 2.

The standard form of a variational equation is:

[4.1]

where H ⊂ V is a linear subspace, ℓ: V → is linear continuous and is such that v → a(u, v) is linear. The standard formulation includes situations where the variational equation is a nonlinear one. For orthogonal projections, only linear or affine situations have to be considered:

1. 1) In the case of the orthogonal projection Px of x V onto a vector subspace H, u = Px H, a(u, v) is the scalar product (u, v), ℓ(v) = (x, v) and H = S.
2. 2) In the case of the orthogonal projection Px of x V onto an affine subspace S = S₀ + {x₀} (S₀ vector subspace, x₀ V), u = Px − u₀, a(u, v) is the scalar product (u, v), ℓ(v) = (x − x₀, v) and H = S₀.

Approximations of the solution of the variational equation [4.1] are generated by considering a total family on S, denoted by F = {φ_i}_i. and looking for an approximated solution having the form:

where the coefficients U = (u_{1, … ,} u_k)^tk have to be determined. More generally, we may consider a sequence of finite families such that F = _kF_k is a total family on S − this is the situation when finite element approximations are used. In both these situations, S is approximated by:

and the variational equation becomes:

Since both v → a(u, v) and v → ℓ(v) are linear, we have

Let us introduce G: ^k → ^k given by:

Then, U is the solution of the algebraical system:

i.e.

If

with a₁ bilinear and a₀ linear, we have.

and

where A is the n × n matrix given by:

while B is the k × l matrix given by:

In this case, U is the solution of the linear system

4.5. Reducing multiple indexes to a single one

The main applications of variational equations in engineering concern Sobolev spaces such as, for instance, V = H⁰(Ω) =

For , with d > 1, these spaces become Cartesian products of spaces , such as, for instance, , .

In these situations, the simplest way to generate a total multidimensional family for a space V is to consider products of total families on . For instance, let be such that _m F_m is a total family on . Then we may consider:

Then, . In order to apply the methods previously exposed, it becomes necessary to transform the multi-index i = (i₁, i₂, … , i_d) into a single index. Such a transformation is standard in the framework of finite elements. For instance, we may use the transformations:

For a two-dimensional (2D) region Ω ⊂ ², these transformations lead to:

The number of unknowns to be determined is . Into an analogous way, the coefficient u_j, correspond to a multidimensionally indexed such that

For a three-dimensional (3D) region Ω ⊂ ³, the transformation leads to:

The number of unknowns to be determined is . In an analogous way, the coefficient u_j, corresponds to a multidimensionally indexed such that:

4.6. Existence and uniqueness of the solution of a variational equation

The reader will find in the literature a large number of results concerning the existence and uniqueness of solutions of variational equations, among all the result known as the theorem of Lax-Milgram [LAX 54], from Peter David Lax and Arthur Norton Milgram.

We give below one of these results, containing the essential assumptions and which applies to nonlinear situations. Let us consider the variational equation:

We have:

THEOREM 4.6.– Assume that:

• i) H is a Hilbert space or a closed vector subspace of a Hilbert space;
• ii) v → a(u, v)is linear, ∀v H;
• iii) ℓ:H→ is linear continuous;
• iv) ∃M such that:
  
• v) such that:
  

Then there exists a unique uV such that:

PROOF.– From (vi) and Riesz’s theorem, we have:

and the variational equation reads as A(u) = f_ℓ or, equivalently,

This equation may be reformulated as:

i.e.

where P_H is the orthogonal projection onto H. We have:

Thus

so that

and

Thus,

Moreover,

and we have:

so that,

and

Taking

We have,

so that F is a contraction and the result yields from Banach’s fixed point theorem (theorem 3.11).

4.7. Linear variational equations in separable spaces

Let us consider the situation where a(, ) is bilinear, i.e.

In this case, conditions (iv)–(v) in theorem 4.6 are equivalent to:

This situation corresponds to the classical result [LAX 54].

When the space H is separable, we may consider a Hilbert basis F ={φ_n:n ^*} ⊂ H and consider the sequence {u_n : n ^*} defined as:

We observe that u_n is determined by solving a linear system:

where

Then, u_n is uniquely determined and is given by:

Moreover,

so that,

and is bounded. As a consequence, there is a subsequence such that (weakly). Thus, Riezs’s theorem shows that:

Indeed, there exists w_ℓ H such that ℓ(v) = (w_ℓ, v), ∀v H and, as a consequence, . Moreover, we have:

so that (strongly). Thus, ∀v H:

Let us denote by P_nv the orthogonal projection of v H on to H_n.

Then,∀v H:

From theorem 3.21 (iii), we obtain:

The uniqueness of u shows that . Thus, theorem 3.5 shows that u_n → u.

4.8. Parametric variational equations

In some situations, we are interested in the solution of variational equations depending upon a parameter. For instance, let us consider the situation where a and/or ℓ depends on a parameter θ:

In this situation, the solution u = u_θ depends upon θ and we may

consider:

i.e. the coefficients of the expansion depend upon θ. In this case, the approach presented in section 4.4 leads to parametric equalities which may be solved by the methods introduced in section 2.2 (other methods of approximation may be found in [SOU 15]). Indeed, using the same notation of section 4.4, we have

so that is the solution of the algebraical system:

which may be solved as in section 2.2: assuming that the functional space where u_j = u_j(θ) is chosen is a separable Hilbert space, we may consider a convenient Hilbert basis and the expansion:

The coefficients may be determined as in section 2.2. This approach may be reinterpreted as follows: we consider the expansion as:

Finite dimensional approximations are obtained by truncation. For instance,

Let us collect all the unknowns in a vector U of kn elements: we may use the map ind₂(i, j) = (i − 1)n + j, so that, for m = ind₂ (i, j), . Let . Then, we look for a vector U such that:

Then, U is the solution of the algebraical system,

4.9. A Matlab® class for variational equations.

The numerical solution of variational equations is performed analogously to the determination of orthogonal projections or weak derivatives. Let us assume that a subprogram avareq evaluates the value of a(u, v) and a subprogram ell evaluates ℓ(v). Both v → a(u, v) and v → ℓ(v) are linear.

In the general situation, u → a(u, v) is nonlinear and we must solve a system of nonlinear algebraic equations G(U) = 0. Assume that a use a subprogram eqsolver solves these equations – for instance, we may look for the minimum of ||G(U)||or call the Matlab® program fsolve, if the Optimization Toolbox is available. If u → a(u, v) is linear, G(U) = AU – B and the equations correspond to a linear system, so that we may use linear solvers, such as the anti-slash operator of Matlab®.

Under these assumptions, we may use the class below:

The variational equation is nonlinear and its solution is u(x) = tan (x). We have:

a and e may be evaluated as follows:

sp = @(u,v) scalar_product.sp0(u,v,xlim,'subprogram');
avareq = @(u,v) a1(u, v,sp,b);
ell = @(v) ell1(v,sp);

where a1 and ell1 are defined in Program 4.3 below.

Results obtained using the family and the family , i > 1 are shown in Figure 4.3.

EXAMPLE 4.9.– Let us consider a = 0, b = 1 and the variational equation:

Here

In this case, the problem is linear. Since u(0) = 0, we eliminate the function constant equal to one from the basis and we consider the families and . The results are shown in Figure 4.4.

4.10. Exercises

EXERCISE 4.1.– Let Ω = (0,1) and .

• 1) Show that ℓ is linear.
• 2) Let :
  • a) Show that there exists such that .
  • b) Conclude that there exists one and only one u V such that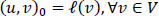
  • c) Show that u(x) = 1 on Ω.
• 3) Let V = H¹(Ω):
  • a) Show that there exists such that: ∀v V: |ℓ(v)| ≤ M||v||_1,1.
  • b) Conclude that there exists one and only one u V such that .
  • c) Show that
• 4) Let V = H¹(Ω), but .
  • a) Let v V.
    Verify that :
    – show that
    – conclude that
    – show that
  • b) Conclude that there exists one and only one u V such that
  • c) Show that −u″ = 1 on .
• 5) Let , with the scalar product (, )_{1, 0}.
  • a) Le tv V:
    – verify that
    – conclude that
    – show that there exists M such that: .
  • b) Conclude that there exists one and only one u V such that .
  • c) Show that .

    

EXERCISE 4.2– Let and ℓ(v) = v(0).

• 1) Show that ℓ is linear.
• 2) Let and . Show that . Conclude verifies
• 3) Let V = H¹(Ω):
  • a) Verify that:
    
  • b) Show that:
    
  • c) Conclude that:
    

    and show that .

  • d) Conclude that ℓ: V → is continuous.
• 4) Let , but consider .
  • a) Verify that .
  • b) Use the equality to show that .
  • c) Conclude that there exists one and only one u V such that .

    

EXERCISE 4.3.– Let Ω = (0,1), a Ω and . Let and .

• 1) Verify that (, ) is a scalar product on V.
• 2) Show that:
• 3) Show that .
• 4) Show that .
• 5) Conclude that there exists M such that .
• 6) Show that there exists one and only one u V such that .

  

EXERCISE 4.4.– Let us consider the variational equation (ƒ )

1) Let us consider the trigonometrical basis , with φ₀ = 1 and, for k > 0:

Let . Determine the coefficients u_n as functions of ƒ. Draw a graphic of the solution for ƒ = −1 and compare it to:

2) Let us consider the polynomial basis F = {φ_n: n }, with φ_n = xⁿ. Let . Determine the coefficients u_n as functions of ƒ. Draw a graphic of the solution for ƒ = −1 and compare it to u¹.

3) Consider the family F = {φ_n: n } of the P1 shape functions

Determine the coefficients u_n as functions of f. Draw a graphic of the solution for f = −l and compare it to u¹.