The Basics of Projective Geometry

The relation that maps a set of points in the physical world  with coordinates (X_i, Y_i, Z_i) to the points on the projection screen with coordinates (x_i, y_i) is called a projective transform.  When you are working with such transforms, it is convenient to use what are known as homogeneous coordinates. The homogeneous coordinates associated with a point in a projective space of dimension n are typically expressed as an (n + 1)-dimensional vector (e.g., x, y, z becomes x, y, z, w), with the additional restriction that any two points whose values are proportional are, in fact, equivalent points. In our case, the image plane is the projective space and it has two dimensions, so we will represent points on that plane as three-dimensional vectors . Recalling that all points having proportional values in the projective space are equivalent, we can recover the actual pixel coordinates by dividing through by q₃. This allows us to arrange the parameters that define our camera (i.e., f_x, f_y, c_x and c_y) into a single 3 × 3 matrix, which  we will call the camera intrinsics matrix.⁶ The projection of the points in the physical world into the camera is now summarized by the following simple form:

where:

Multiplying this out, you will find that w = Z and so, since the point is in homogeneous coordinates, we can divide through by w (or Z) in order to recover our earlier definitions. The minus sign is gone because we are now looking at the noninverted image on the projective plane in front of the pinhole rather than the inverted image on the projection screen behind the pinhole.

While we are on the topic of homogeneous coordinates, there are a few functions in the OpenCV library that are appropriate to introduce here. The functions cv::convertPointsToHomogeneous() and cv::convertPointsFromHomogeneous() allow us to convert to and from homogeneous coordinates.⁷ They have the following prototypes:

void cv::convertPointsToHomogeneous(
  cv::InputArray  src,        // Input vector of N-dimensional points
  cv::OutputArray dst         // Result vector of (N+1)-dimensional points
);

void cv::convertPointsFromHomogeneous(
  cv::InputArray  src,        // Input vector of N-dimensional points
  cv::OutputArray dst         // Result vector of (N-1)-dimensional points
);

The first function expects a vector of N-dimensional points (in any of the usual representations) and constructs a vector of (N + 1)-dimensional points from that vector. All of the entries of the newly constructed vector associated with the added dimension are set to 1. The result is that:

The second function does the conversion back from homogeneous coordinates. Given an input vector of points of dimension N, it constructs a vector of (N – 1)-dimensional points by first dividing all of the components of each point by the value of the last components of the point’s representation and then throwing away that component. The result is that:

With the ideal pinhole, we have a useful model for some of the three-dimensional geometry of vision. Remember, however, that very little light goes through a pinhole; thus, in practice, such an arrangement would make for very slow imaging while we wait for enough light to accumulate on whatever imager we are using. For a camera to form images at a faster rate, we must gather a lot of light over a wider area and bend (i.e., focus) that light to converge at the point of projection. To accomplish this, we use a lens. A lens can focus a large amount of light on a point to give us fast imaging, but it comes at the cost of introducing distortions.

Rodrigues Transform

When dealing with three-dimensional spaces, one most often represents rotations in that space by 3 × 3 matrices. This representation is usually the most convenient because multiplying a vector by this matrix is equivalent to rotating the vector in some way. The downside is that it can be difficult to intuit just what 3 × 3 matrix goes with what rotation. Briefly, we are going to introduce an alternative representation for such rotations that is used by some of the OpenCV functions in this chapter, as well as a useful function for converting to and from this alternative representation.

This alternate, and somewhat easier-to-visualize,⁸ representation for a rotation is essentially a vector about which the rotation operates together with a single angle. In this case it is standard practice to use only a single vector whose direction encodes the direction of the axis to be rotated around, and to use the length of the vector to encode the amount of rotation in a counterclockwise direction. This is easily done because the direction can be equally well represented by a vector of any magnitude; hence, we can choose the magnitude of our vector to be equal to the magnitude of the rotation. The relationship between these two representations, the matrix and the vector, is captured by the Rodrigues transform.⁹

Let be the three-dimensional vector ; this vector implicitly defines θ, the magnitude of the rotation by the length (or magnitude) of . We can then convert from this axis-magnitude representation to a rotation matrix R as follows:

We can also go from a rotation matrix back to the axis-magnitude representation by using:

Thus we find ourselves in the situation of having one representation (the matrix representation) that is most convenient for computation and another representation (the Rodrigues representation) that is a little easier on the brain. OpenCV provides us with a function for converting from either representation to the other:

void cv::Rodrigues(
  cv::InputArray  src,                     // Input rotation vector or matrix
  cv::OutputArray dst,                     // Output rotation matrix or vector
  cv::OutputArray jacobian = cv::noArray() // Optional Jacobian (3x9 or 9x3)
);

Suppose we have the vector and need the corresponding rotation matrix representation R; we set src to be the 3 × 1 vector and dst to be the 3 × 3 rotation matrix R. Conversely, we can set src to be a 3 × 3 rotation matrix R and dst to be a 3 × 1 vector . In either case, cv::Rodrigues() will do the right thing. The final argument is optional. If jacobian is something other than cv::noArray(), then it should be a pointer to a 3 × 9 or a 9 × 3 matrix that will be filled with the partial derivatives of the output array components with respect to the input array components. The jacobian outputs are mainly used for the internal optimization of the cv::solvePnP() and cv::calibrateCamera() functions; your use of the cv::Rodrigues() function will mostly be limited to converting the outputs of cv::solvePnP() and cv::calibrateCamera() from the Rodrigues format of 1 × 3 or 3 × 1 axis-angle vectors to rotation matrices. For this, you can leave jacobian set to cv::noArray().

Lens Distortions

In theory, it is possible to define a lens that will introduce no distortions. In practice, however, no lens is perfect. This is mainly for reasons of manufacturing; it is much easier to make a “spherical” lens than to make a more mathematically ideal “parabolic” lens. It is also difficult to mechanically align the lens and imager exactly. Here we describe the two main lens distortions and how to model them.¹⁰ Radial distortions arise as a result of the shape of lens, whereas tangential distortions arise from the assembly process of the camera as a whole.

We start with radial distortion. The lenses of real cameras often noticeably distort the location of pixels near the edges of the imager. This bulging phenomenon is the source of the “barrel” or “fisheye” effect (see the room-divider lines at the top of Figure 18-17 for a good example). Figure 18-3 gives some intuition as to why this radial distortion occurs. With some lenses, rays farther from the center of the lens are bent more than those closer in. A typical inexpensive lens is, in effect, stronger than it ought to be as you get farther from the center. Barrel distortion is particularly noticeable in cheap web cameras but less apparent in high-end cameras, where a lot of effort is put into fancy lens systems that minimize radial distortion.

Figure 18-3. Radial distortion: rays farther from the center of a simple lens are bent too much compared to rays that pass closer to the center; thus, the sides of a square appear to bow out on the image plane (this is also known as barrel distortion)

For radial distortions, the distortion is 0 at the (optical) center of the imager and increases as we move toward the periphery. In practice, this distortion is small and can be characterized by the first few terms of a Taylor series expansion around r = 0.¹¹ For cheap web cameras, we generally use the first two such terms; the first of which is conventionally called k₁ and the second k₂. For highly distorted cameras such as fisheye lenses, we can use a third radial distortion term, k₃. In general, the radial location of a point on the imager will be rescaled according to the following equations:¹²

and:

Here, (x, y) is the original location (on the imager) of the distorted point and is the new location as a result of the correction. Figure 18-4 shows displacements of a rectangular grid that are due to radial distortion. External points on a front-facing rectangular grid are increasingly displaced inward as the radial distance from the optical center increases.

Figure 18-4. Radial distortion plot for a particular camera lens: the arrows show where points on an external rectangular grid are displaced in a radially distorted image (courtesy of Jean-Yves Bouguet)¹³

The second-largest common distortion is tangential distortion. This distortion is due to manufacturing defects resulting from the lens not being exactly parallel to the imaging plane; see Figure 18-5.

Figure 18-5. Tangential distortion results when the lens is not fully parallel to the image plane; in cheap cameras, this can happen when the imager is glued to the back of the camera (image courtesy of Sebastian Thrun)

Tangential distortion is minimally characterized by two additional parameters: p₁ and p₂, such that:¹⁴

and:

Thus in total there are five distortion coefficients that we require. Because all five are necessary in most of the OpenCV routines that use them, they are typically bundled into one distortion vector; this is just a 5 × 1 matrix containing k₁, k₂, p₁, p₂, and k₃ (in that order). Figure 18-6 shows the effects of tangential distortion on a front-facing external rectangular grid of points. The points are displaced elliptically as a function of location and radius.

Figure 18-6. Tangential distortion plot for a particular camera lens: the arrows show where points on an external rectangular grid are displaced in a tangentially distorted image (courtesy of Jean-Yves Bouguet)

There are many other kinds of distortions that occur in imaging systems, but they typically have lesser effects than radial and tangential distortions. Hence, neither we nor OpenCV will deal with them further.

Rotation Matrix and Translation Vector

For each image the camera takes of a particular object, we can describe the pose of the object relative to the camera coordinate system in terms of a rotation and a translation; see Figure 18-8.

Figure 18-8. Converting from object to camera coordinate systems: the point P on the object is seen as point p on the image plane; we relate the point p to point P by applying a rotation matrix R and a translation vector t to P

In general, a rotation in any number of dimensions can be described in terms of multiplication of a coordinate vector by a square matrix of the appropriate size. Ultimately, a rotation is equivalent to introducing a new description of a point’s location in a different coordinate system. Rotating the coordinate system by an angle θ is equivalent to counter-rotating our target point around the origin of that coordinate system by the same angle θ. The representation of a two-dimensional rotation as matrix multiplication is shown in Figure 18-9. Rotation in three dimensions can be decomposed into a two-dimensional rotation around each axis in which the pivot axis measurements remain constant. If we rotate around the x-, y-, and z-axes in sequence¹⁸ with respective rotation angles ψ, φ, and θ, the result is a total rotation matrix R that is given by the product of the three matrices , , and , where:

Figure 18-9. Rotating points by θ (in this case, around the z-axis) is the same as counter-rotating the coordinate axis by θ; by simple trigonometry, we can see how rotation changes the coordinates of a point

Thus . The rotation matrix R has the property that its inverse is its transpose (we just rotate back); hence, we have , where I₃ is the 3 × 3 identity matrix consisting of 1s along the diagonal and 0s everywhere else.

The translation vector is how we represent a shift from one coordinate system to another system whose origin is displaced to another location; in other words, the translation vector is just the offset from the origin of the first coordinate system to the origin of the second coordinate system. Thus, to shift from a coordinate system centered on an object to one centered at the camera, the appropriate translation vector is simply . We then know (with reference to Figure 18-8) that a point in the object (or world) coordinate frame has coordinates in the camera coordinate frame:

Combining this equation for with the camera intrinsic-corrections will form the basic system of equations that we will be asking OpenCV to solve. The solution to these equations will contain the camera calibration parameters we seek.

We have just seen that a three-dimensional rotation can be specified with three angles and that a three-dimensional translation can be specified with the three parameters (x, y, z); thus we have six parameters so far. The OpenCV intrinsics matrix for a camera has four parameters (f_x, f_y, c_x, and c_y), yielding a grand total of 10 parameters that must be solved for each view (but note that the camera-intrinsic parameters stay the same between views). Using a planar object, we’ll soon see that each view fixes eight parameters. Because the six parameters of rotation and translation change between views, for each view we have constraints on two additional parameters that we then use to resolve the camera-intrinsic matrix. Thus, we need (at least) two views to solve for all the geometric parameters.

We’ll provide more details on the parameters and their constraints later in the chapter, but first we’ll discuss the calibration object. The calibration objects used in OpenCV are flat patterns of several types described next. The first OpenCV calibration object was a “chessboard” as shown in Figure 18-10. The following discussion will mostly refer to this type of pattern, but other patterns are available, as we will see.

Calibration Boards

In principle, any appropriately characterized object could be used as a calibration object. One practical choice is a regular pattern on a flat surface, such as a chessboard¹⁹ (see Figure 18-10), circle-grid (see Figure 18-15), randpattern²⁰ (see Figure 18-11), ArUco (see Figure 18-12), or ChArUco patterns²¹ (see Figure 18-13). Appendix C has usable examples of all the calibration patterns available in OpenCV.  Some calibration methods in the literature rely on three-dimensional objects (e.g., a box covered with markers), but flat chessboard patterns are much easier to deal with; among other things, it is rather difficult to make (and to store and distribute) precise three-dimensional calibration objects. OpenCV thus opts for using multiple views of a planar object rather than one view of a specially constructed three-dimensional object. For the moment, we will focus on the chessboard pattern. The use of a pattern of alternating black and white squares (see Figure 18-10) ensures that there is no bias toward one side or the other in measurement. Also, the resulting grid corners lend themselves naturally to the subpixel localization function discussed in Chapter 16. We will also discuss another alternative calibration board, called a circle-grid (see Figure 18-15), which has some desirable properties, and which in some cases may give superior results to the chessboard. For the other patterns, please see the documentation referenced in the figures in this chapter. The authors have had particularly good success using the ChArUco pattern.

Figure 18-10. Images of a chessboard being held at various orientations (left) provide enough information to completely solve for the locations of those images in global coordinates (relative to the camera) and the camera intrinsics

Figure 18-11. A calibration pattern made up of a highly textured random pattern; see the multicamera calibration tutorial in the opencv_contrib/modules/ccalib/tutorial directory²²

Figure 18-12. A calibration pattern made up of a grid of ArUco (2D barcode) squares. Note that because each square is identified by its ArUco pattern, much of the board can be occluded and yet still have enough spatially labeled points to be used in calibration. See “ArUco marker detection (aruco module)” in the OpenCV documentation²³

Figure 18-13. Checkerboard with embedded ArUco (ChArUco). A checkerboard calibration pattern where each corner is labeled with an ArUco (2D barcode) pattern. This allows much of the checkerboard to be occluded while allowing for the higher positional accuracy of corner intersections. See “ArUco marker detection (aruco module)” in the OpenCV documentation²⁴

bool cv::findChessboardCorners(    // Return true if corners were found
  cv::InputArray  image,           // Input chessboard image, 8UC1 or 8UC3
  cv::Size        patternSize,     // corners per row, and per column
  cv::OutputArray corners,         // Output array of detected corners
  int             flags      = cv::CALIB_CB_ADAPTIVE_THRESH
                             | cv::CALIB_CB_NORMALIZE_IMAGE
);

Drawing chessboard corners with cv::drawChessboardCorners()

Particularly when one is debugging, it is often desirable to draw the found chessboard corners onto an image (usually the image that we used to compute the corners in the first place); this way, we can see whether the projected corners match up with the observed corners. Toward this end, OpenCV provides a convenient routine to handle this common task. The function cv::drawChessboardCorners() draws the corners found by cv::findChessboardCorners() onto an image that you provide. If not all of the corners were found, then the available corners will be represented as small red circles. If the entire pattern was found, then the corners will be painted into different colors (each row will have its own color) and connected by lines representing the identified corner order.

void cv::drawChessboardCorners(
  cv::InputOutputArray image,          // Input/output chessboard image, 8UC3
  cv::Size             patternSize,    // Corners per row, and per column
  cv::InputArray       corners,        // corners from findChessboardCorners()
  bool                 patternWasFound // Returned from findChessboardCorners()
);

The first argument to cv::drawChessboardCorners() is the image to which the drawing will be done. Because the corners will be represented as colored circles, this must be an 8-bit color image. In most cases, this will be a copy of the image you gave to cv::findChessboardCorners() (but you must convert it to a three-channel image yourself, if it wasn’t already). The next two arguments, patternSize and corners, are the same as the corresponding arguments for cv::findChessboardCorners(). Finally, the argument patternWasFound indicates whether the entire chessboard pattern was successfully found; this can be set to the return value from cv::findChessboardCorners(). Figure 18-14 shows the result of applying cv::drawChess​boardCorners() to a chessboard image.

We now turn to what a planar object such as the calibration board can do for us. Points on a plane undergo a perspective transformation when viewed through a pinhole or lens. The parameters for this transform are contained in a 3 × 3 homography matrix, which we will describe shortly, after a brief discussion of an alternative pattern to square grids.

Figure 18-14. Result of cv::drawChessboardCorners(); once you find the corners using cv::findChessboardCorners(), you can project where these corners were found (small circles on corners) and in what order they belong (as indicated by the lines between circles)

Circle-grids and cv::findCirclesGrid()

An alternative to the chessboard is the circle-grid. Conceptually, the circle-grid is similar to the chessboard, except that rather than an array of alternating black and white squares, the board contains an array of black circles on a white background.

Calibration with a circle-grid proceeds exactly the same as with cv::findChessboardCorners() and the chessboard, except that a different function is called and a different calibration image is used. That different function is cv::findCirclesGrid(), and it has the following prototype:

bool cv::findCirclesGrid(// Return true if corners were found
  cv::InputArray  image,           // Input chessboard image, 8UC1 or 8UC3
  cv::Size        patternSize,     // corners per row, and per column
  cv::OutputArray centers,         // Output array of detected circle centers
  int             flags      = cv::CALIB_CB_SYMMETRIC_GRID,
  const cv::Ptr<cv::FeatureDetector>& blobDetector
                             = new SimpleBlobDetector()
);

Like cv::findChessboardCorners(), it takes an image and a cv::Size object defining the number (and arrangement) of the circle pattern. It outputs the location of the centers, which are equivalent to the corners in the chessboard.

The flags argument tells the function what sort of array the circles are arranged into. By default, cv::findCirclesGrid() expects a symmetric grid of circles. A “symmetric” grid is a grid in which the circles are arranged neatly into rows and columns in the same way as the chessboard corners. The alternative is an asymmetric grid. We use the asymmetric grid by setting the flags argument to cv::CALIB_CB_ASYMMETRIC_GRID. In an “asymmetric” grid, the circles in each row are staggered transverse to the row. (The grid shown in Figure 18-15 is an example of an asymmetric grid.)

Figure 18-15. With the regular array of circles (upper left), the centers of the circles function analogously to the corners of the chessboard for calibration. When seen in perspective (lower right), the deformation of the circles is regular and predictable

When you are using an asymmetric grid, it is important to remember how rows and columns are counted. By way of example, in the case shown in Figure 18-15, because it is the rows that are “staggered,” then the array shown has only 4 rows, and 11 columns. The final option for flags is cv::CALIB_CB_CLUSTERING. It can be set along with cv::CALIB_CB_SYMMETRIC_GRID or cv::CALIB_CB_ASYMMETRIC_GRID with the logical OR operator. If this option is selected, then cv::findCirclesGrid() will use a slightly different algorithm for finding the circles. This alternate algorithm is more robust to perspective distortions, but (as a result) is also a lot more sensitive to background clutter. This is a good choice when you are trying to calibrate a camera with an unusually wide field of view.

Note

In general, one often finds the asymmetric circle-grid to be superior to the chessboard, both in terms of the quality of final results, as well as the stability of those results between multiple runs. For these reasons, asymmetric circle-grids increasingly became part of the standard toolkit for camera calibration. In very modern times, patterns such as ChArUco (see the contrib experimental code section of the library) are gaining significant traction as well. 

Homography

In computer vision, we define planar homography as a projective mapping from one plane to another.²⁷ Thus, the mapping of points on a two-dimensional planar surface to the imager of our camera is an example of planar homography. It is possible to express this mapping in terms of matrix multiplication if we use homogeneous coordinates to express both the viewed point and the point on the imager to which is mapped. If we define:

then we can express the action of the homography simply as:

Here we have introduced the parameter s, which is an arbitrary scale factor (intended to make explicit that the homography is defined only up to that factor). It is conventionally factored out of H, and we’ll stick with that convention here.

With a little geometry and some matrix algebra, we can solve for this transformation matrix. The most important observation is that H has two parts: the physical transformation, which essentially locates the object plane we are viewing, and the projection, which introduces the camera intrinsics matrix. See Figure 18-16.

Figure 18-16. View of a planar object as described by homography: a mapping—from the object plane to the image plane—that simultaneously comprehends the relative locations of those two planes as well as the camera projection matrix

The physical transformation part is the sum of the effects of some rotation R and some translation that relate the plane we are viewing to the image plane. Because we are working in homogeneous coordinates, we can combine these within a single matrix as follows:²⁸

Then, the action of the camera matrix M, which we already know how to express in projective coordinates, is multiplied by , which yields:

where:

It would seem that we are done. However, it turns out that in practice our interest is not the coordinate that is defined for all of space, but rather a coordinate that is defined only on the plane we are looking at. This allows for a slight simplification.

Without loss of generality, we can choose to define the object plane so that Z = 0. We do this because, if we also break up the rotation matrix into three 3 × 1 columns (i.e., ), then one of those columns is no longer needed. In particular:

The homography matrix H that maps a planar object’s points onto the imager is then described completely by , where:

Observe that H is now a 3 × 3 matrix.²⁹

OpenCV uses the preceding equations to compute the homography matrix. It uses multiple images of the same object to compute both the individual translations and rotations for each view as well as the intrinsics (which are the same for all views). As we have discussed, rotation is described by three angles and translation is defined by three offsets; hence there are six unknowns for each view. This is OK, because a known planar object (such as our chessboard) gives us eight equations—that is, the mapping of a square into a quadrilateral can be described by four (x, y) points. Each new frame gives us eight equations at the cost of six new extrinsic unknowns, so given enough images we should be able to compute any number of intrinsic unknowns (more on this shortly).

The homography matrix H relates the positions of the points on a source image plane to the points on the destination image plane (usually the imager plane) by the following simple equations:

Notice that we can compute H without knowing anything about the camera intrinsics. In fact, computing multiple homographies from multiple views is the method OpenCV uses to solve for the camera intrinsics, as we’ll see.

OpenCV provides us with a handy function, cv::findHomography(), that takes a list of correspondences and returns the homography matrix that best describes those correspondences. We need a minimum of four points to solve for H, but we can supply many more if we have them³⁰ (as we will with any chessboard bigger than 3 × 3). Using more points is beneficial, because invariably there will be noise and other inconsistencies whose effect we would like to minimize:

cv::Mat cv::findHomography(
  cv::InputArray  srcPoints,                 // Input array source points (2-d)
  cv::InputArray  dstPoints,                 // Input array result points (2-d)
  cv::int         method                = 0, // 0, cv::RANSAC, cv::LMEDS, etc.
  double          ransacReprojThreshold = 3, // Max reprojection error
  cv::OutputArray mask                  = cv::noArray() // use only non-zero pts
);

The input arrays srcPoints and dstPoints contain the points in the original plane and the target plane, respectively. These are all two-dimensional points, so they must be N × 2 arrays, N × 1 arrays of CV_32FC2 elements, or STL vectors of cv::Point2f objects (or any combination of these).

The input called method determines the algorithm that will be used to compute the homography. If left as the default value of 0, all of the points will be considered and the computed result will be the one that minimizes the reprojection error. In this case, the reprojection error is the sum of squared Euclidean distances between H times the “original” points and the target points.

Conveniently, fast algorithms exist to solve such problems in the case of an error metric of this kind. Unfortunately, however, defining the error in this way leads to a system in which outliers—individual data points that seem to imply a radically different solution than the majority—tend to have a drastic effect on the solution. In practical cases such as camera calibration, it is common that measurement errors will produce outliers, and the resulting solution will often be very far from the correct answer because of these outliers. OpenCV provides three robust fitting methods that can be used as an alternative, and tend to give much better behavior in the presence of noise.

The first such option, which we select by setting method to cv::RANSAC, is the RANSAC method (also known as the “random sampling with consensus” method). In the RANSAC method, subsets of the provided points are selected at random, and a homography matrix is computed for just that subset. It is then refined by all of the remaining data points that are roughly consistent with that initial estimation. The “inliers” are those that are consistent, while the “outliers” are those that are not. The RANSAC algorithm computes many such random samplings, and keeps the one that has the largest portion of inliers. This method is extremely efficient in practice for rejecting noisy outlier data and finding the correct answer.

The second alternative is the LMeDS algorithm (also known as the “least median of squares” algorithm). As the name suggests, the idea behind LMeDS is to minimize the median error, as opposed to what is essentially the mean squared error minimized by the default method.³¹

The advantage of LMeDS is that it does not need any further information or parameters to run. The disadvantage is that it will perform well only if the inliers constitute at least a majority of the data points. In contrast, RANSAC can function correctly and give a satisfactory answer given almost any signal-to-noise ratio. The cost of this, however, is that you will have to tell RANSAC what constitutes “roughly consistent”—the maximum distance reprojected points can be from its source and still be considered worth including in the refined model. If you are using the cv::RANSAC method, then the input ransacReprojThreshold controls this distance. If you are using any other method, this parameter can be ignored.

Finally, there is RHO algorithm, introduced in [Bazargani15] and available in OpenCV 3, which is based on a “weighted” RANSAC modification called PROSAC and runs faster in the case of many outliers.

The final argument, mask, is used only with the robust methods, and it is an output. If an array is provided, cv::findHomography() will fill that array indicating which points were actually used in the best computation of H.

The return value will be a 3 × 3 matrix. Because there are only eight free parameters in the homography matrix, we chose a normalization where H₃₃ = 1 (which is usually possible except for the quite rare singular case H₃₃ = 0). Scaling the homography could be applied to the ninth homography parameter, but usually prefer to instead scale by multiplying the entire homography matrix by a scale factor, as described earlier in this chapter.

Camera Calibration

We finally arrive at camera calibration for camera intrinsics and distortion parameters. In this section, we’ll explain how to compute these values using cv::calibrateCamera() and also how to use these models to correct distortions in the images that the calibrated camera would have otherwise produced. First we will say a little more about just how many views of a chessboard are necessary in order to solve for the intrinsics and distortion. Then we’ll offer a high-level overview of how OpenCV actually solves this system before moving on to the code that makes it all easy to do.

What’s under the hood?

This subsection is for those who want to go deeper; it can be safely skipped if you just want to call the calibration functions.

If you’re still with us, the question remains: how does the actual mathematics work for calibration? Although there are many ways to solve for the camera parameters, OpenCV chose one that works well on planar objects. The algorithm OpenCV uses to solve for the focal lengths and offsets is based on Zhang’s method [Zhang00], but OpenCV uses a different method based on Brown [Brown71] to solve for the distortion parameters.

To get started, we pretend that there is no distortion in the camera while solving for the other calibration parameters. For each view of the chessboard, we collect a homography H, as described previously (i.e., a map from the physical object to the imager). We’ll write H out as column vectors, , where each h is a 3 × 1 vector. Then, in view of the preceding homography discussion, we can set H equal to the camera intrinsics matrix M multiplied by a combination of the first two rotation matrix columns, and , and the translation vector . After we include the scale factor s, this yields:

Reading off these equations, we have:

with:

The rotation vectors are orthogonal to each other by construction, and since the scale is extracted we can take and to be orthonormal. Orthonormal implies two things: the rotation vector’s dot product is 0, and the vectors’ magnitudes are equal. Starting with the dot product, we have:

For any vectors and we have , so we can substitute for and to derive our first constraint:

where M^–T is shorthand for (M^–1)^T. We also know that the magnitudes of the rotation vectors are equal:

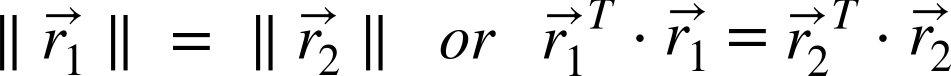
Substituting for and yields our second constraint:

To make things easier to manage, we define B = M^–T · M^–1. Writing this out, we have:

It so happens that this matrix B has a general closed-form solution:

Using the B-matrix, both constraints have the general form in them. Let’s multiply this out to see what the components are. Because B is symmetric, it can be written as one six-dimensional vector dot product. Arranging the necessary elements of B into the new vector , we have:

Using this definition for , our two constraints may now be written as:

If we collect K images of chessboards together, then we can stack K of these equations together:

where V is a 2 · K × 6 matrix. As before, if K ≥ 2 then this equation can be solved for our vector . The camera intrinsics are then pulled directly out of our closed-form solution for the B-matrix:

and:

with:

The extrinsics (rotation and translation) are then computed from the equations we read off of the homography condition:

and:

Here the scaling parameter is determined from the orthonormality condition . Some care is required because, when we solve using real data and put the r-vectors together (), we will not likely end up with an exact rotation matrix for which holds.³³

To get around this problem, the usual trick is to take the singular value decomposition (SVD) of R. As discussed in Chapter 5, SVD is a method of factoring a matrix into two orthonormal matrices, U and V, and a middle matrix D of scale values on its diagonal. This allows us to turn R into . Because R is itself orthonormal, the matrix D must be the identity matrix I₃ such that . We can thus “coerce” our computed R into being a rotation matrix by taking R’s singular value decomposition, setting its D matrix to the identity matrix, and multiplying by the SVD again to yield our new, conforming rotation matrix R.

Despite all this work, we have not yet dealt with lens distortions. We use the camera intrinsics found previously—together with the distortion parameters set to 0—for our initial guess to start solving a larger system of equations.

The points we “perceive” on the image are really in the wrong place owing to distortion. Let (x_p, y_p) be the point’s location if the pinhole camera were perfect and let (x_d, y_d) be its distorted location; then:

We use the results of the calibration without distortion using the following substitution:³⁴

A large list of these equations are collected and solved to find the distortion parameters, after which the intrinsics and extrinsics are re-estimated. That’s the heavy lifting that the single function cv::calibrateCamera()³⁵ does for you!

double cv::calibrateCamera(
  cv::InputArrayOfArrays  objectPoints,    // K vecs (N pts each, object frame)
  cv::InputArrayOfArrays  imagePoints,     // K vecs (N pts each, image frame)
  cv::Size                imageSize,       // Size of input images (pixels)
  cv::InputOutputArray    cameraMatrix,    // Resulting 3-by-3 camera matrix
  cv::InputOutputArray    distCoeffs,      // Vector of 4, 5, or 8 coefficients
  cv::OutputArrayOfArrays rvecs,           // Vector of K rotation vectors
  cv::OutputArrayOfArrays tvecs,           // Vector of K translation vectors
  int                     flags       = 0, // Flags control calibration options
  cv::TermCriteria        criteria    = cv::TermCriteria(
    cv::TermCriteria::COUNT | cv::TermCriteria::EPS,
    30,                                    // ...after this many iterations
    DBL_EPSILON                            // ...at this total reprojection error
  )
);

bool cv::solvePnP(
  cv::InputArray  objectPoints,              // Object points (object frame)
  cv::InputArray  imagePoints,               // Found pt locations (img frame)
  cv::InputArray  cameraMatrix,              // 3-by-3 camera matrix
  cv::InputArray  distCoeffs,                // Vector of 4, 5, or 8 coeffs
  cv::OutputArray rvec,                      // Result rotation vector
  cv::OutputArray tvec,                      // Result translation vector
  bool            useExtrinsicGuess = false, // true='use vals in rvec and tvec'
  int             flags             = cv::ITERATIVE
);

bool cv::solvePnPRansac(
  cv::InputArray  objectPoints,              // Object points (object frame)
  cv::InputArray  imagePoints,               // Found pt locations (img frame)
  cv::InputArray  cameraMatrix,              // 3-by-3 camera matrix
  cv::InputArray  distCoeffs,                // Vector of 4, 5, or 8 coeffs
  cv::OutputArray rvec,                      // Result rotation vector
  cv::OutputArray tvec,                      // Result translation vector
  bool            useExtrinsicGuess = false, // read vals in rvec and tvec ?
  int             iterationsCount   = 100,   // RANSAC iterations
  float           reprojectionError = 8.0,   // Max error for inclusion
  int             minInliersCount   = 100,   // terminate if this many found
  cv::OutputArray inliers           = cv::noArray(), // Contains inlier indices
  int flags                         = cv::ITERATIVE  // same as solvePnP()
)

Undistortion Maps

When performing undistortion on an image, we must specify where every pixel in the input image is to be moved in the output image. Such a specification is called an undistortion map (or sometimes just a distortion map). There are several representations available for such maps.

The first and most straightforward representation is the two-channel float representation. In this representation, a remapping for an N × M image is represented by an N × M array of two-channel floating-point numbers as shown in Figure 18-18. For any given entry (i, j) in the image, the value of that entry will be a pair of numbers (i^*, j^*) indicating the location to which pixel (i, j) of the input image should be relocated. Of course, because (i^*, j^*) are floating-point numbers, interpolation in the target image is implied.⁴¹

Figure 18-18. In the float-float representation, two different floating-point arrays, the X-map and the Y-map, encode the destination of a pixel at (i, j) in the original image. A pixel at (i, j) is mapped to (x_map(i, j), y_map(i, j)) in the destination image. Because that destination is not necessarily integer, the interpolation is used to compute the final image pixel intensities

The next representation is the two-array float representation. In this representation, the remapping is described by a pair of N × M arrays, each of which is a single-channel floating-point array. The first of these arrays contains at location (i, j) the value i^*, the x-coordinate of the remapped location of pixel (i, j) from the original array. Similarly, the second array contains at the same location j^*, the y-coordinate of the remapped location of pixel (i, j).

The final representation is the fixed-point representation. In this representation, a mapping is specified by a two-channel signed integer array (i.e., of type CV_16SC2). The interpretation of this array is the same as the two-channel float representation, but operations with this format are much faster. In the case in which higher precision is required, the necessary information required for interpolation during the remapping is encoded in a second single-channel unsigned integer array (i.e., CV_16UC1). The entries in this array refer to an internal lookup table, which is used for the interpolation (and thus there are no “user-serviceable parts” in this array).

Converting Undistortion Maps Between Representations with cv::convertMaps()

Because there are multiple representations available for undistortion maps, it is natural that one might want to convert between them. We do this with the cv::convertMaps() function. This function allows you to provide a map in any of the four formats we just discussed, and convert it into any of the others. The prototype for cv::convertMaps() is the following:

void cv::convertMaps(
  cv::InputArray  map1,          // First in map: CV_16SC2/CV_32FC1/CV_32FC2
  cv::InputArray  map2,          // Second in map: CV_16UC1/CV_32FC1 or none
  cv::OutputArray dstmap1,       // First out map
  cv::OutputArray dstmap2,       // Second out map
  int             dstmap1type,   // dstmap1 type: CV_16SC2/CV_32FC1/CV_32FC2
  bool            nninterpolation = false  // For conversion to fixed point types
);

The inputs map1 and map2 are your existing maps, and the outputs dstmap1 and dstmap2 are the outputs where the converted maps will be stored. The argument dstmap1type tells cv::convertMaps() what sort of maps to create for you; from the type specified here, the remapping you want is then inferred. You use the final argument, nninterpolation, when converting to the fixed point type to indicate whether you would like the interpolation tables to be computed as well. The possible conversions are shown in Table 18-1, along with the correct settings for dstmap1type and nninterpolation for each conversion.

Note that, because the conversion from floating point to fixed point naturally loses precision (even if nninterpolation is used), if you convert one way and then convert back again, you should not expect to necessarily receive back exactly what you started with.

Computing Undistortion Maps with cv::initUndistortRectifyMap()

Now that we understand undistortion maps, the next step is to see how to compute them from camera parameters. In fact, distortion maps are much more general than just this one specific situation, but for our current purpose, the interesting thing is to know how we can use the results of our camera calibrations to create nicely rectified images. So far, we have been discussing the situation of monocular imaging. In fact, one of the more important applications of rectification is in preparing a pair of images to be used for stereoscopic computation of depth images. We will get back to the topic of stereo in the next chapter, but it is worth keeping this application in mind, partially because some of the arguments to the functions that do undistortion are primarily for use in that stereo vision context.

The basic process is to first compute the undistortion maps, and then to apply them to the image. The reason for this separation is that, in most practical applications, you will compute the undistortion maps for your camera only once, and then you will use those maps again and again as new images come streaming in from your camera. The function cv::initUndistortRectifyMap() computes the distortion map from camera-calibration information:

void cv::initUndistortRectifyMap(
  cv::InputArray  cameraMatrix,           // 3-by-3 camera matrix
  cv::InputArray  distCoeffs,             // Vector of 4, 5, or 8 coefficients
  cv::InputArray  R,                      // Rectification transformation
  cv::InputArray  newCameraMatrix,        // New camera matrix (3-by-3)
  cv::Size        size,                   // Undistorted image size
  int             m1type,                 // 'map1' type: 16SC2, 32FC1, or 32FC2
  cv::OutputArray map1,                   // First output map
  cv::OutputArray map2,                   // Second output map
);

The function cv::initUndistortRectifyMap() computes the undistortion map (or maps). The first two arguments are the camera intrinsic matrix and the distortion coefficients, both in the form you received them from cv::calibrateCamera().

The next argument, R, may be used or, alternatively, set to cv::noArray(). If used, it must be a 3 × 3 rotation matrix, which will be preapplied before rectification. The function of this matrix is to compensate for a rotation of the camera relative to some global coordinate system in which that camera is embedded.

Similar to the rotation matrix, newCameraMatrix can be used to affect how the images are undistorted. If used, it will “correct” the image before undistortion to how it would have looked if taken from a different camera with different intrinsic parameters. In practice, the aspect that one changes in this way is the camera center, not the focal length. You will typically not use this when dealing with monocular imaging, but it is important in the case of stereo image analysis. For monocular images, you will typically just set this argument to cv::noArray().

The argument size simply sets the size of the output maps; this should correspond to the size of images you will be undistorting.

The final three arguments—m1type, map1, and map2—specify the final map type and provide a place for that map to be written, respectively. The possible values of m1type are CV_32FC1 or CV_16SC2, and correspond to the type that will be used to represent map1. In the case of CV_32FC1, map2 will also be of type CV_32FC1. This corresponds to the two-array float representation of the map we encountered in the previous section. In the case of CV_16SC2, map1 will be in the fixed-point representation (recall that this single-channel array contains the interpolation table coefficients).

Undistorting an Image with cv::remap()

Once you have computed the undistortion maps, you can apply them to incoming images using cv::remap(). We encountered cv::remap() earlier, when discussing general image transforms; this is one specific, but very important, application for that function.

As we saw previously, the cv::remap() function has two map arguments that correspond to the undistortion maps, such as those computed by cv::initUndistortRectifyMap(). cv::remap() will accept any of the distortion map formats we have discussed: the two-channel float, the two-array float, or the fixed-point format (with or without the accompanying array of interpolation table indexes).

Undistortion with cv::undistort()

In some cases, you will either have only one image to rectify, or need to recompute the undistortion maps for every image. In such cases, you can use the somewhat more compact cv::undistort(), which effectively computes the maps and applies them in a single go.

void cv::undistort(
  cv::InputArray  src,                        // Input distorted image
  cv::OutputArray dst,                        // Result corrected image
  cv::InputArray  cameraMatrix,               // 3-by-3 camera matrix
  cv::InputArray  distCoeffs,                 // Vector of 4, 5, or 8 coeffs
  cv::InputArray  newCameraMatrix = noArray() // Optional new camera matrix
);

The arguments to cv::undistort() are identical to the corresponding arguments to cv::initUndistortRectifyMap().

Sparse Undistortion with cv::undistortPoints()

Another situation that arises occasionally is that, rather than rectifying an entire image, you have a set of points you have collected from an image, and you care only about the location of those points. In this case, you can use cv::undistortPoints() to compute the “correct” locations for your specific list of points:

void cv::undistortPoints(
  cv::InputArray  src,                             // Input array, N pts. (2-d)
  cv::OutputArray dst,                             // Result array, N pts. (2-d)
  cv::InputArray  cameraMatrix,                    // 3-by-3 camera matrix
  cv::InputArray  distCoeffs,                      // Vector of 4, 5, or 8 coeffs
  cv::InputArray  R               = cv::noArray(), // 3-by-3 rectification mtx.
  cv::InputArray  P               = cv::noArray()  // 3-by-3 or 3-by-4 new camera
                                                   //   or new projection matrix
);

As with cv::undistort(), the arguments to cv::undistortPoints() are analogous to the corresponding arguments to cv::initUndistortRectifyMap(). The primary difference is that the src and dst arguments are vectors of two-dimensional points, rather than two-dimensional arrays. (As always, these vectors can be of any of the usual forms: N × 1 array of cv::Vec2i objects, N × 1 array of float objects, an STL-style vector of cv::Vec2f objects, etc.)

The argument P of cv::undistortPoints() corresponds to newCameraMatrix of cv::undistortPoints(). As before, these two extra parameters relate primarily to the function’s use in stereo rectification, which we will discuss in Chapter 19. The rectified camera matrix P can have dimensions of 3 × 3 or 3 × 4 deriving from the first three or four columns of cv::stereoRectify()’s return value for camera matrices P1 or P2 (for the left or right camera; see Chapter 19). These parameters are by default cv::noArray(), which the function interprets as identity matrices.