CHAPTER 5
Pairs of Random Variables
The previous two chapters dealt with the theory of single random variables. However, many problems of practical interest require the modeling of random phenomenon using two or maybe even more random variables. This chapter extends the theory of Chapters 3 and 4 to consider pairs of random variables. Chapter 6 then generalizes these results to include an arbitrary number of random variables. A common example that involves two random variables is the study of a system with a random input. Due to the randomness of the input, the output will naturally be random as well. Quite often it is necessary to characterize the relationship between the input and the output. A pair of random variables can be used to characterize this relationship: one for the input and another for the output.
Another class of examples involving random variables are those involving spatial coordinates in two dimensions. A pair of random variables can be used to probabilistically describe the position of an object which is subject to various random forces. There are endless examples of situations where we are interested in two random quantities that may or may not be related to one another, for example, the height and weight of a student, or the grade point average and GRE scores of a student, or the temperature and relative humidity at a certain place and time.
To start with, consider an experiment E whose outcomes lie in a sample space,S. A two-dimensional random variable is a mapping of the points in the sample space to ordered pairs {x, y}. Usually, when dealing with a pair of random variables, the sample space naturally partitions itself so that it can be viewed as a combination of two simpler sample spaces. For example, suppose the experiment was to observe the height and weight of a typical student. The range of student heights could fall within some set which we call sample space S1, while the range of student weights could fall within the space S2. The overall sample space of the experiment could then be viewed as S = S1 x S2. For any outcome s ∈ S of this experiment, the pair of random variables (X, Y) is merely a mapping of the outcome s to a pair of numerical values (x(s), y(s)). In the case of our height/weight experiment, it would be natural to choose x(s) to be the height of the student (in inches perhaps), while y(s) is the weight of the student (in pounds). Note that it is probably not sufficient to consider two separate experiments, one where the student’s height is measured and assigned to the random variable X and another where a student’s weight is measured and assigned to the random variable Y.
While the density functions fX (x) and fY (y) do partially characterize the experiment, they do not completely describe the situation. It would be natural to expect that the height and weight are somehow related to each other. While it may not be very rare to have a student 74 in. tall nor unusual to have a student who weighs 120 pounds, it is probably rare indeed to have a student who is both 74 in. tall and weighs 120 pounds. A careful reading of the wording in the previous sentence makes it clear that in order to characterize the relationship between a pair of random variables, it is necessary to look at the joint probabilities of events relating to both random variables. We accomplish this through the joint cumulative distribution function (CDF) and the joint probability density function (PDF) in the next two sections.
5.1 Joint Cumulative Distribution Functions
When introducing the idea of random variables in Chapter 3, we started with the notion of a CDF. In the same way, to probabilistically describe a pair of random variables, {X, Y}, we start with the notion of a joint CDF.
Definition 5.1: The joint CDF of a pair of random variables, {X, Y}, is FXY , (x, y) = Pr(X ≤ x, Y ≤ y). That is, the joint CDF is the joint probability of the two events {X ≤ x} and {Y ≤ y}.
As with the CDF of a single random variable, not any function can be a joint CDF. The joint CDF of a pair of random variables will satisfy properties similar to those satisfied by the CDFs of single random variables. First of all, since the joint CDF is a probability, it must take on a value between 0 and 1. Also, since the random variables X and Y are real valued, it is impossible for either to take on a value less than −∞ and both must be less than ∞. Hence, F X, Y (x, y) evaluated at either x = −∞ or y = −∞ (or both) must be zero and FX , Y (∞,∞) must be one. Next, for x1≤x2 and y1≤y2, {X≤x1} ∩ {Y≤y1} is a subset of {X≤x2} ∩ {Y≤y2} so that FX , Y (x1, y1)≤FX , Y (x2, y2). That is, the CDF is a monotonic, nondecreasing function of both x and y. Note that since the event { {X≤∞} must happen, then {X≤∞} ∩ {Y≤y} = {Y≤y} so that FX , Y (∞, y) = FY (y). Likewise, FX , Y (x, ∞) = FX (x). In the context of joint CDFs, FX (x) and FY (y) are referred to as the marginal CDFs of X and Y, respectively.
Finally, consider using a joint CDF to evaluate the probability that the pair of random variables (X, Y) falls into a rectangular region bounded by the points (x1, y1), (x2, y1), (x1, y2), and (x2, y2). This calculation is illustrated in Figure 5.1. The desired rectangular region is the lightly shaded area. Evaluating FX , Y (x2, y2) gives the probability that the random variable falls anywhere below or to the left of the point (x2, y2); this includes all of the area in the desired rectangle, but it also includes everything below and to the left of the desired rectangle. The probability of the random variable falling to the left of the rectangle can be subtracted off using FX , Y (x1, y2). Similarly, the region below the rectangle can be subtracted off using FX , Y (x2, y1); these are the two medium-shaded regions in Figure 5.1. In subtracting off these two quantities, we have subtracted twice the probability of the pair falling both below and to the left of the desired rectangle (the dark-shaded region). Hence we must add back this probability using FX ,Y (x1, y1). All of these properties of joint CDFs are summarized as follows:

Figure 5.1 Illustrating the evaluation of the probability of a pair of random variables falling in a rectangular region.
With the exception of property (4), all of these properties are analogous to the ones listed in Equation (3.3) for CDFs of single random variables.
Property (5) tells us how to calculate the probability of the pair of random variables falling in a rectangular region. Often, we are interested in also calculating the probability of the pair of random variables falling in a region which is not rectangular (e.g., a circle or triangle). This can be done by forming the required region using many infinitesimal rectangles and then repeatedly applying property (5). In practice, however, this task is somewhat overwhelming, and hence we do not go into the details here.
Example 5.1
One of the simplest examples (conceptually) of a pair of random variables is one which is uniformly distributed over the unit square (i.e., 0 ≤ x ≤ 1, 0 ≤ y ≤ 1). The CDF of such a random variable is

Even this very simple example leads to a rather cumbersome function. Nevertheless, it is straightforward to verify that this function does indeed satisfy all the properties of a joint CDF. From this joint CDF, the marginal CDF of X can be found to be

Hence, the marginal CDF of X is also a uniform distribution. The same statement holds for Y as well.
5.2 Joint Probability Density Functions
As seen in Example 5.1, even the simplest joint random variables can lead to CDFs which are quite unwieldy. As a result, working with joint CDFs can be difficult. In order to avoid extensive use of joint CDFs, attention is now turned to the two dimensional equivalent of the PDF.
Definition 5.2: The joint probability density function of a pair of random variables (X, Y) evaluated at the point (x, y) is
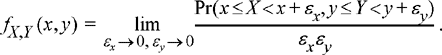 (5.2)
(5.2)
Similar to the one-dimensional case, the joint PDF is the probability that the pair of random variables (X, Y) lies in an infinitesimal region defined by the point (x, y) normalized by the area of the region.
For a single random variable, the PDF was the derivative of the CDF. By applying Equation (5.1e) to the definition of the joint PDF, a similar relationship is obtained.
Theorem 5.1: The joint PDF fX,Y (x, y) can be obtained from the joint CDF FX,Y (x, Y) by taking a partial derivative with respect to each variable. That is,
 (5.3)
(5.3)
Proof: Using Equation (5.1e),
 (5.4)
(5.4)
Dividing by εx and taking the limit as εx → 0 results in
 (5.5)
(5.5)
Then dividing by εy and taking the limit as εy → 0 gives the desired result:
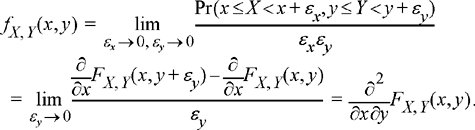 (5.6)
(5.6)
This theorem shows that we can obtain a joint PDF from a joint CDF by differentiating with respect to each variable. The converse of this statement would be that we could obtain a joint CDF from a joint PDF by integrating with respect to each variable. Specifically,
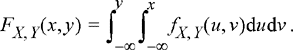 (5.7)
(5.7)
Example 5.2
From the joint CDF given in Example 5.1, it is found (by differentiating the joint CDF with respect to both x and y) that the joint PDF for a pair of random variables uniformly distributed over the unit square is
![]()
Note how much simpler the joint PDF is to specify than is the joint CDF.
From the definition of the joint PDF in Equation (5.2) as well as the relationships specified in Equations (5.3) and (5.7), several properties of joint PDFs can be inferred. These properties are summarized as follows:
Property (1) follows directly from the definition of the joint PDF in Equation (5.2) since both the numerator and denominator there are nonnegative. Property (2) results from the relationship in Equation (5.7) together with the fact that FX, Y
(∞,∞) = 1. This is the normalization integral for joint PDFs. These first two properties form a set of sufficient conditions for a function of two variables to be a valid joint PDF. Properties (3) and (4) have already been developed. Property (5) is obtained by first noting that the marginal CDF of X is FX
(x) = FX, Y
(x, ∞). Using Equation (5.7) then results in ![]() . Differentiating this expression with respect to x produces the expression in property (5) for the marginal PDF of x. A similar derivation produces the marginal PDF of y. Hence, the marginal PDFs are obtained by integrating out the unwanted variable in the joint PDF. The last property is obtained by combining Equations (5.1e) and (5.7).
. Differentiating this expression with respect to x produces the expression in property (5) for the marginal PDF of x. A similar derivation produces the marginal PDF of y. Hence, the marginal PDFs are obtained by integrating out the unwanted variable in the joint PDF. The last property is obtained by combining Equations (5.1e) and (5.7).
Example 5.3
Suppose two random variables are jointly uniformly distributed over the unit circle. That is, the joint PDF fX , Y (x, y) is constant anywhere such that x2 + y2 ≤ 1:
![]()
The constant c can be determined using the normalization integral for joint PDFs:
![]()
The marginal PDF of X is found by integrating y out of the joint PDF:
![]()
By symmetry, the marginal PDF of Y would have the same functional form:
![]()
Although X and Y were jointly uniformly distributed, the marginal distributions are not uniform. Stated another way, suppose we are given just the marginal PDFs of X and Y as just specified. This information alone is not enough to determine the joint PDF. One may be able to form many joint PDFs that produce the same marginal PDFs. For example, suppose we form

It is easy to verify that this is a valid joint PDF and leads to the same marginal PDFs. Yet, this is clearly a completely different joint PDF than the uniform distribution with which we started. This reemphasizes the need to specify the joint distributions of random variables and not just their marginal distributions.
Property (6) of joint PDFs given in Equation (5.8f) specifies how to compute the probability that a pair of random variables takes on a value in a rectangular region. Often, we are interested in computing the probability that the pair of random variables falls in a region which is not rectangularly shaped. In general, suppose we wish to compute Pr((X, Y) ∈ A), where A is the region illustrated in Figure 5.2. This general region can be approximated as a union of many nonoverlapping rectangular regions as shown in the figure. In fact, as we make the rectangles ever smaller, the approximation improves to the point where the representation becomes exact in the limit as the rectangles get infinitely small. That is, any region can be represented as an infinite number of infinitesimal rectangular regions so that A = ∪ Ri , where Ri represents the ith rectangular region. The probability that the random pair falls in A is then computed as
 (5.9)
(5.9)

Figure 5.2 Approximation of an arbitrary region by a series of infinitesimal rectangles.
The sum of the integrals over the rectangular regions can be replaced by an integral over the original region A:
 (5.10)
(5.10)
This important result shows that the probability of a pair of random variables falling in some two-dimensional region A is found by integrating the joint PDF of the two random variables over the region A.
Example 5.4
Suppose a pair of random variables has the joint PDF given by
![]()
The probability that the point (X, Y) falls inside the unit circle is given by

Converting this integral to polar coordinates results in

Example 5.5
Now suppose that a pair of random variables has the joint PDF given by
![]()
First, the constant c is found using the normalization integral
![]()
Next, suppose we wish to determine the probability of the event {X>Y}. This can be viewed as finding the probability of the pair (X, Y) falling in the region A that is now defined as A = {(x, y):x > y}. This probability is calculated as
![]()
Example 5.6
![]() In many cases, evaluating the probability of a pair a random variables falling in some region may be quite difficult to calculate analytically. For example, suppose we modify Example 5.4 so that the joint PDF is now of the form
In many cases, evaluating the probability of a pair a random variables falling in some region may be quite difficult to calculate analytically. For example, suppose we modify Example 5.4 so that the joint PDF is now of the form
![]()
Again, we would like to evaluate the probability that the pair (X, Y) falls in the unit circle. To do this analytically we must evaluate

Converting to polar coordinates the integral becomes
![]()
Either way the double integral looks formidable. We can enlist MATLAB to help in one of two ways. First, we could randomly generate many samples of the pair of random variables according to the specified distribution and count the relative frequency of the number that falls within the unit circle. Alternatively, we can get MATLAB to calculate one of the preceding double integrals numerically. We will take the latter approach here and evaluate the double integral in polar coordinates. First, we must define a MATLAB function to evaluate the integrand:
![]()
MATLAB will then evaluate the integral by executing the command
![]()
By executing these MATLAB commands, we find the value of the integral to be 0.002072.
5.3 Joint Probability Mass Functions
When the random variables are discrete rather than continuous, it is often more convenient to work with probability mass functions (PMFs) rather than PDFs or CDFs. It is straightforward to extend the concept of the PMF to a pair of random variables.
Definition 5.3: The joint PMF for a pair of discrete random variables X and Y is given by PX, Y (x, y) = Pr({X=x} ∩ {Y=y}).
In particular, suppose the random variable X takes on values from the set {x1, x2, …, xM } and the random variable Y takes on values from the set {y1, y2, …, yN . Here, either M or N could be potentially infinite, or both could be finite. Several properties of the joint PMF analogous to those developed for joint PDFs should be apparent.
Furthermore, the joint PDF or the joint CDF of a pair of discrete random variables can be related to the joint PMF through the use of delta functions or step functions by
 (5.12)
(5.12)
 (5.13)
(5.13)
Usually, it is most convenient to work with PMFs when the random variables are discrete. However, if the random variables are mixed (i.e., one is discrete and one is continuous), then it becomes necessary to work with PDFs or CDFs since the PMF will not be meaningful for the continuous random variable.
Example 5.7
Two discrete random variables N and M have a joint PMF given by
![]()
The marginal PMF of N can be found by summing over m in the joint PMF:
![]()
To evaluate this series, the following identity is used:
![]()
The marginal PMF then reduces to

Likewise, by symmetry, the marginal PMF of M is
![]()
Hence, the random variables M and N both follow a geometric distribution.
5.4 Conditional Distribution, Density, and Mass Functions
The notion of conditional distribution functions and conditional density functions was first introduced in Chapter 3. In this section, those ideas are extended to the case where the conditioning event is related to another random variable. For example, we might want to know the distribution of a random variable representing the score a student achieves on a test given the value of another random variable representing the number of hours the student studied for the test. Or, perhaps we want to know the probability density function of the outside temperature given that the humidity is known to be below 50%.
To start with, consider a pair of discrete random variables X and Y with a PMF, PX , Y (x, y). Suppose we would like to know the PMF of the random variable X given that the value of Y has been observed. Then, according to the definition of conditional probability
 (5.14)
(5.14)
We refer to this as the conditional PMF of X given Y. By way of notation we write![]()
Example 5.8
Using the joint PMF given in Example 5.7 along with the marginal PMF found in that example, it is found that
![]()
Note that the conditional PMF of N given M is quite different than the marginal PMF of N. That is, knowing M changes the distribution of N.
The simple result developed in Equation (5.14) can be extended to the case of continuous random variables and PDFs. The following theorem shows that the PMFs in (5.14) can simply be replaced by PDFs.
Theorem 5.2: The conditional PDF of a random variable X given that Y = y is
 (5.15)
(5.15)
Proof: Consider the conditioning event A= y≤ Y ≤ y + dy. Then

Passing to the limit as dy → 0, the event A becomes the event {Y = y}, producing the desired result.
Integrating both sides of this equation with respect to x produces the appropriate result for CDFs:
 (5.16)
(5.16)
Usually, the conditional PDF is much easier to work with, so the conditional CDF will not be discussed further.
Example 5.9
A certain pair of random variables has a joint PDF given by
![]()
for some positive constants a, b, and c. The marginal PDFs are easily found to be
![]()
The conditional PDF of X given Y then works out to be
![]()
The conditional PDF of Y given X could also be determined in a similar way:
![]()
Example 5.10
This example involves two Gaussian random variables. Suppose X and Y have a joint PDF given by
![]()
The marginal PDF is found as follows:
![]()
In order to evaluate the integral, complete the square in the exponent:
![]()
Now the integrand is a Gaussian-looking function. If the appropriate constant is added to the integrand, the integrand will be a valid PDF and hence must integrate out to one. In this case, the constant we need to add to the integrand to make the integral unity is ![]() . Stated another way, the integral as just written must evaluate to
. Stated another way, the integral as just written must evaluate to ![]() . Hence, the marginal PDF of X is
. Hence, the marginal PDF of X is
![]()
and we see that X is a zero-mean, unit-variance, Gaussian (i.e., standard normal) random variable. By symmetry, the marginal PDF of Y must also be of the same form. The conditional PDF of X given Y is

So, the conditional PDF of X given Y is also Gaussian. But, given that it is known that Y = y, the mean of X is now y/2 (instead of zero), and the variance of X is 3/4 (instead of one). In this example, knowledge of Y has shifted the mean and reduced the variance of X.
In addition to conditioning on a random variable taking on a point value such as Y = y, the conditioning can also occur on an interval of the form y1 ≤ Y≤y2. To simplify notation, let the conditioning event A be A = {y1 ≤ Y ≤ y2}. The relevant conditional PMF, PDF, and CDF are then given, respectively, by
 (5.17)
(5.17)
 (5.18)
(5.18)
 (5.19)
(5.19)
It is left as an exercise for the reader to derive these expressions.
Example 5.11
Using the joint PDF of Example 5.10, suppose we want to determine the conditional PDF of X given that Y>yo. The numerator in Equation (5.18) is calculated according to

Since the marginal PDF of Y is a zero-mean, unit-variance Gaussian PDF, the denominator of Equation (5.18) becomes
![]()
Therefore, the PDF of X conditioned on Y>yo is

Note that when the conditioning event was a point condition on Y, the conditional PDF of X was Gaussian; yet, when the conditioning event is an interval condition on Y, the resulting conditional PDF of X is not Gaussian at all.
5.5 Expected Values Involving Pairs of Random Variables
The notion of expected value is easily generalized to pairs of random variables. To begin, we define the expected value of an arbitrary function of two random variables.
Definition 5.4: Let g(x, y) be an arbitrary two-dimensional function. The expected value of g(X, Y), where X and Y are random variables, is
![]() (5.20)
(5.20)
For discrete random variables, the equivalent expression in terms of the joint PMF is
![]() (5.21)
(5.21)
If the function g(x, y) is actually a function of only a single variable, say x, then this definition reduces to the definition of expected values for functions of a single random variable as given in Definition 4.2.
 (5.22)
(5.22)
To start with, consider an arbitrary linear function of the two variables g(x, y) = ax + by, where a and b are constants. Then
 (5.23)
(5.23)
This result merely states that expectation is a linear operation.
In addition to the functions considered in Chapter 4 which led to statistics such as means, variances, and the like, functions involving both variables x and y will be considered here.
These new functions will lead to statistics that will partially characterize the relationships between the two random variables.
Definition 5.5: The correlation between two random variables is defined as
![]() (5.24)
(5.24)
Furthermore, two random variables which have a correlation of zero are said to be orthogonal.
One instance in which the correlation appears is in calculating the second moment of a sum of two random variables. That is, consider finding the expected value of g(X, Y) = (X + Y)2.
![]() (5.25)
(5.25)
Hence the second moment of the sum is the sum of the second moments plus twice the correlation.
Definition 5.6: The covariance between two random variables is
![]() (5.26)
(5.26)
If two random variables have a covariance of zero, they are said to be uncorrelated.
The correlation and covariance are strongly related to one another as shown by the following theorem.
Proof: 
As a result, if either X or Y (or both) has a mean of zero, correlation and covariance are equivalent. The covariance function occurs when calculating the variance of a sum of two random variables.
![]() (5.28)
(5.28)
This result can be obtained from Equation (5.25) by replacing X with X –μX and Y with Y –μY.
Another statistical parameter related to a pair of random variables is the correlation coefficient, which is nothing more than a normalized version of the covariance.
Definition 5.7: The correlation coefficient of two random variables X and Y, ρXY , is defined as
 (5.29)
(5.29)
The next theorem quantifies the nature of the normalization. In particular, it shows that a correlation coefficient can never be more than 1 in absolute value.
Theorem 5.4: The correlation coefficient is less than 1 in magnitude.
Proof: Consider taking the second moment of X + aY, where a is a real constant:
![]()
Since this is true for any a, we can tighten the bound by choosing the value of a that minimizes the left-hand side. This value of a turns out to be
![]()
Plugging in this value gives

If we replace X with X – μX and Y with Y – μY the result is
![]()
Rearranging terms then gives the desired result:
![]() (5.30)
(5.30)
Note that we can also infer from the proof that equality holds if Y is a constant times X. That is, a correlation coefficient of 1 (or –1) implies that X and Y are completely correlated (knowing Y determines X). Furthermore, uncorrelated random variables will have a correlation coefficient of zero. Therefore, as its name implies, the correlation coefficient is a quantitative measure of the correlation between two random variables. It should be emphasized at this point that zero correlation is not to be confused with independence. These two concepts are not the same (more on this later).
The significance of the correlation, covariance, and correlation coefficient will be discussed further in the next two sections. For now, we present an example showing how to compute these parameters.
Example 5.12
Consider once again the joint PDF of Example 5.10. The correlation for these random variables is
![]()
In order to evaluate this integral, the joint PDF is rewritten ![]() and then those terms involving only x are pulled outside the inner integral over y.
and then those terms involving only x are pulled outside the inner integral over y.
![]()
The inner integral (in square brackets) is the expected value of a Gaussian random variable with a mean of x/2 and variance of 3/4 which thus evaluates to x/2. Hence,
![]()
The remaining integral is the second moment of a Gaussian random variable with zero-mean and unit variance which integrates to 1. The correlation of these two random variables is therefore E[XY]=1/2. Since both X and Y have zero means, Cov(X, Y) is also equal to 1/2. Finally, the correlation coefficient is also ρXY = 1/2 due to the fact that both X and Y have unit variance.
The concepts of correlation and covariance can be generalized to higher-order moments as given in the following definition.
Definition 5.8: The (m, n)th joint moment of two random variables X and Y is
![]() (5.31)
(5.31)
The (m, n)th joint central moment is similarly defined as
![]() (5.32)
(5.32)
These higher-order joint moments are not frequently used and therefore are not considered further here.
As with single random variables, a conditional expected value can also be defined for which the expectation is carried out with respect to the appropriate conditional density function.
Definition 5.9: The conditional expected value of a function g(X) of a random variable X given that Y = y is
![]() (5.33)
(5.33)
Conditional expected values can be particularly useful in calculating expected values of functions of two random variables that can be factored into the product of two one-dimensional functions. That is, consider a function of the form g(x, y) = g1(x)g2(y). Then
![]() (5.34)
(5.34)
From Equation (5.15) the joint PDF is rewritten as fX ,Y (x, y) = fY X (y x)fX (x), resulting in
 (5.35)
(5.35)
Here, the subscripts on the expectation operator have been included for clarity to emphasize that the outer expectation is with respect to the random variable X, while the inner expectation is with respect to the random variable Y (conditioned on X). This result allows us to break a two-dimensional expectation into two one-dimensional expectations. This technique was used in Example 5.12, where the correlation between two variables was essentially written as
![]() (5.36)
(5.36)
In that example, the conditional PDF of Y given X was Gaussian, thus finding the conditional mean was accomplished by inspection. The outer expectation then required finding the second moment of a Gaussian random variable, which is also straightforward.
5.6 Independent Random Variables
The concept of independent events was introduced in Chapter 2. In this section, we extend this concept to the realm of random variables. To make that extension, consider the events A = {X ≤ x} and B = {Y≤y} related to the random variables X and Y. The two events A and B are statistically independent if Pr(A, B) = Pr(A)Pr(B). Restated in terms of the random variables, this condition becomes
![]() (5.37)
(5.37)
Hence, two random variables are statistically independent if their joint CDF factors into a product of the marginal CDFs. Differentiating both sides of this equation with respect to both x and y reveals that the same statement applies to the PDF as well. That is, for statistically independent random variables, the joint PDF factors into a product of the marginal PDFs:
![]() (5.38)
(5.38)
It is not difficult to show that the same statement applies to PMFs as well. The preceding condition can also be restated in terms of conditional PDFs. Dividing both sides of Equation (5.38) by fX (x) results in
![]() (5.39)
(5.39)
A similar result involving the conditional PDF of X given Y could have been obtained by dividing both sides by the PDF of Y. In other words, if X and Y are independent, knowing the value of the random variable X should not change the distribution of Y and vice versa.
Example 5.13
Returning once again to the joint PDF of Example 5.10, we saw in that example that the marginal PDF of X is
![]()
while the conditional PDF of X given Y is
![]()
Clearly, these two random variables are not independent.
Example 5.14
Suppose the random variables X and Y are uniformly distributed on the square defined by 0 ≤ x, y ≤ 1. That is
![]()
The marginal PDFs of X and Y work out to be
![]()
These random variables are statistically independent since fX , Y (x, y) = fX (x)fY (y).
Theorem 5.5: Let X and Y be two independent random variables and consider forming two new random variables U = g1 (X) and V = g2(Y). These new random variables U and V are also independent.
Proof: To show that U and V are independent, consider the events A = {U≤u} and B = {V≤v}. Next define the region R u to be the set of all points x such that g1 (x) ≤ u. Similarly, define R to be the set of all points y such that g2(y) ≤ v. Then

Since X and Y are independent, their joint PDF can be factored into a product of marginal PDFs resulting in

Since we have shown that F U, V (u, v) = FU (u)FV(v), the random variables U and V must be independent.
Another important result deals with the correlation, covariance, and correlation coefficients of independent random variables.
Theorem 5.6: If X and Y are independent random variables, then E[XY] = μXμY , Cov(X, Y) = 0, and ρX ,Y = 0.
Proof: 
The conditions involving covariance and correlation coefficient follow directly from this result.
Therefore, independent random variables are necessarily uncorrelated, but the converse is not always true. Uncorrelated random variables do not have to be independent as demonstrated by the next example.
Example 5.15
Consider a pair of random variables X and Y that are uniformly distributed over the unit circle so that

The marginal PDF of X can be found as follows:
![]()
By symmetry, the marginal PDF of Y must take on the same functional form. Hence, the product of the marginal PDFs is
![]()
Clearly, this is not equal to the joint PDF, and therefore, the two random variables are dependent. This conclusion could have been determined in a simpler manner. Note that if we are told that X = 1, then necessarily Y = 0, whereas if we know that X = 0, then Y can range anywhere from –1 to 1. Therefore, conditioning on different values of X leads to different distributions for Y.
Next, the correlation between X and Y is calculated.
![]()
Since the inner integrand is an odd function (of y) and the limits of integration are symmetric about zero, the integral is zero. Hence, E[XY] = 0. Note from the marginal PDFs just found that both X and Y are zero-mean. So, it is seen for this example that while the two random variables are uncorrelated, they are not independent.
Example 5.16
![]() Suppose we wish to use MATLAB to generate samples of a pair of random variables (X, Y) that are uniformly distributed over the unit circle. That is, the joint PDF is
Suppose we wish to use MATLAB to generate samples of a pair of random variables (X, Y) that are uniformly distributed over the unit circle. That is, the joint PDF is

If we generated two random variables independently according to the MATLAB code: X=rand(1); Y=rand(1); this would produce a pair of random variables uniformly distributed over the square 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. One way to achieve the desired result is to generate random variables uniformly over some region which includes the unit circle and then only keep those pairs of samples which fall inside the unit circle. In this case, it is straightforward to generate random variables which are uniformly distributed over the square, –1 ≤ x ≤ 1,–1 ≤ y ≤ 1, which circumscribes the unit circle. Then we keep only those samples drawn from within this square that also fall within the unit circle. The code that follows illustrates this technique. We also show how to generate a three-dimensional plot of an estimate of the joint PDF from the random data generated. To get a decent estimate of the joint PDF, we need to generate a rather large number of samples (we found that 100,000 worked pretty well). This requires that we create and perform several operations on some very large vectors. Doing so tends to make the program run slowly. In order to speed up the operation of the program, we choose to create shorter vectors of random variables (1000 in this case) and then repeat the procedure several times (100 in this case). Although this makes the code a little longer and probably a little harder to follow, by avoiding the creation of very long vectors, it substantially speeds up the program. The results of this program are shown in Figure 5.3.

Figure 5.3 Estimate of the joint PDF of a pair of random variables uniformly distributed over the unit circle from the data generated in Example 5.16. (For color version of this figure, the reader is referred to the web version of this chapter.)


5.7 Jointly Gaussian Random Variables
As with single random variables, the most common and important example of a two-dimensional probability distribution is that of a joint Gaussian distribution. We begin by defining what is meant by a joint Gaussian distribution.
Definition 5.10: A pair of random variables X and Y is said to be jointly Gaussian if their joint PDF is of the general form
 (5.40)
(5.40)
where μX and μY are the means of X and Y, respectively; σX and σY are the standard deviations of X and Y, respectively; and ρXY is the correlation coefficient of X and Y.
It is left as an exercise for the reader (see Exercise 5.35) to verify that this joint PDF results in marginal PDFs that are Gaussian. That is,
 (5.41)
(5.41)
It is also left as an exercise for the reader (see Exercise 5.36) to demonstrate that if X and Y are jointly Gaussian, then the conditional PDF of X given Y = y is also Gaussian, with a mean of μX+ρXY(σX/σY)(y−μY) and a variance of σX 2(1 – ρX 2 Y ). An example of this was shown in Example 5.10, and the general case can be proven following the same steps shown in that example.
Figure 5.4 shows the joint Gaussian PDF for three different values of the correlation coefficient. In Figure 5.4a, the correlation coefficient is ρXY = 0 and thus the two random variables are uncorrelated (and as we will see shortly, independent). Figure 5.4b shows the joint PDF when the correlation coefficient is large and positive, ρXY = 0.9. Note how the surface has become taller and thinner and largely lies above the line y = x. In Figure 5.4c, the correlation is now large and negative, ρXY = –0.9. Note that this is the same picture as in Figure 5.4b, except that it has been rotated by 90°. Now the surface lies largely above the line y = –x. In all three figures, the means of both X and Y are zero and the variances of both X and Y are 1. Changing the means would simply translate the surface but would not change the shape. Changing the variances would expand or contract the surface along either the X – or Y-axis depending on which variance was changed.


Figure 5.4 The joint Gaussian PDF: (a) μX =μY = 0, σX =σY =1, ρXY =0; (b) μX =μY =0, σX = σY = 1, ρXY = 0.9; (c) μX = μY = 0, σX = σY = 1, ρXY = –0.9.
Example 5.17
The joint Gaussian PDF is given by

Suppose we equate the portion of this equation that is within the square brackets to a constant. That is,
![]()
This is the equation for an ellipse. Plotting these ellipses for different values of c results in what is known as a contour plot. Figure 5.5 shows such plots for the two-dimensional joint Gaussian PDF. The following code can be used to generate such plots. The reader is encouraged to try creating similar plots for different values of the parameters in the Gaussian distribution.

Figure 5.5 Estimate of the joint PDF of a pair of random variables uniformly distributed over the unit circle from the data generated in Example 5.16. (For color version of this figure, the reader is referred to the web version of this chapter.)


Theorem 5.7: Uncorrelated Gaussian random variables are independent.
Proof: Uncorrelated Gaussian random variables have a correlation coefficient of zero. Plugging ρXY = 0 into the general joint Gaussian PDF results in

This clearly factors into the product of the marginal Gaussian PDFs.

While Example 5.15 demonstrated that this property does not hold for all random variables, it is true for Gaussian random variables. This allows us to give a stronger interpretation to the correlation coefficient when dealing with Gaussian random variables. Previously, it was stated that the correlation coefficient is a quantitative measure of the amount of correlation between two variables. While this is true, it is a rather vague statement. After all, what does “correlation” mean? In general, we cannot equate correlation and statistical dependence. Now, however, we see that in the case of Gaussian random variables, we can make the connection between correlation and statistical dependence. Hence, for jointly Gaussian random variables, the correlation coefficient can indeed be viewed as a quantitative measure of statistical dependence. This relationship is illustrated in Figure 5.6.

Figure 5.6 Interpretation of the correlation coefficient for jointly Gaussian random variables.
5.8 Joint Characteristic and Related Functions
When computing the joint moments of random variables, it is often convenient to use characteristic functions, moment-generating functions, or probability-generating functions. Since a pair of random variables is involved, the “frequency domain” function must now be two dimensional. We start with a description of the joint characteristic function which is similar to a two-dimensional Fourier transform of the joint PDF.
Definition 5.11: Given a pair of random variables X and Y with a joint PDF, fX ,Y (x, y), the joint characteristic function is
![]() (5.42)
(5.42)
The various joint moments can be evaluated from the joint characteristic function using techniques similar to those used for single random variables. It is left as an exercise for the reader to establish the following relationship:
 (5.43)
(5.43)
Example 5.18
Consider a pair of zero-mean, unit-variance, jointly Gaussian random variables whose joint PDF is
![]()
One way to calculate the joint characteristic function is to break the problem into two one-dimensional problems.
![]()
Conditioned on Y, X is a Gaussian random variable with a mean of ρY and a variance of 1–ρ2. The general form of the characteristic function (one-dimensional) of a Gaussian random variable with mean μX and variance σX 2 is (see Example 4.20)
![]()
Therefore, the inner expectation above evaluates to
![]()
The joint characteristic function is then
![]()
The remaining expectation is the characteristic function of a zero-mean, unit-variance Gaussian random variable evaluated at ω= ρω1 +ω2. The resulting joint characteristic function is then found to be
![]()
From this expression, various joint moments can be found. For example, the correlation is

Since the two random variables were zero mean, Cov(X, Y) = ρ. Furthermore, since the two random variables were unit variance, ρ is also the correlation coefficient. We have proved therefore that the parameter ρ that shows up in the joint Gaussian PDF is indeed the correlation coefficient.
We could easily compute higher-order moments as well. For example, suppose we needed to compute E[X2 Y2]. It can be computed in a similar manner to the preceding:

Definition 5.12: For a pair of discrete random variables defined on a two-dimensional lattice of nonnegative integers, one can define a joint probability-generating function as
 (5.44)
(5.44)
The reader should be able to show that the joint partial derivatives of the joint probability-generating function evaluated at zero are related to the terms in the joint PMF, whereas those same derivatives evaluated at 1 lead to joint factorial moments. Specifically:
 (5.45)
(5.45)
 (5.46)
(5.46)
Example 5.19
Consider the joint PMF given in Example 5.7:
![]()
It is not too difficult to work out the joint probability-generating function for this pair of discrete random variables.

It should be noted that the closed form expression used for the various series preceding limits the range in the (z1, z2) plane for which these expressions are valid; thus, care must be taken when evaluating this function and its derivatives at various points. However, for this example, the expression is valid in and around the points of interest (i.e., (z1, z2) = (0, 0) and (z1, z2) = (1, 1)).
Now that the joint probability-generating function has been found, joint moments are fairly easy to compute. For example,

Putting these two results together, it is found that
![]()
By symmetry, we can also conclude that E[NM(M – 1)] = 6ab2 and E[NM2] = 6ab2 + 2ab. As one last example, we note that

From this and the previous results, we can find E[N2 M2] as follows:
![]()
The moment-generating function can also be generalized in a manner virtually identical to what was done for the characteristic function. We leave the details of this extension to the reader.
5.9 Transformations of Pairs of Random Variables
In this section, we consider forming a new random variable as a function of a pair of random variables. When a pair of random variables is involved, there are two classes of such transformations. The first class of problems deals with the case when a single new variable is created as a function of two random variables. The second class of problems involves creating two new random variables as two functions of two random variables. These two distinct, but related, problems are treated in this section.
Consider first a single function of two random variables, Z = g(X, Y). If the joint PDF of X and Y is known, can the PDF of the new random variable Z be found? Of course, the answer is yes, and there are a variety of techniques to solve these types of problems depending on the nature of the function g(![]() ). The first technique to be developed is an extension of the approach we used in Chapter 4 for functions of a single random variable.
). The first technique to be developed is an extension of the approach we used in Chapter 4 for functions of a single random variable.
The CDF of Z can be expressed in terms of the variables X and Y as
 (5.47)
(5.47)
The inequality g(x, y) ≤ z defines a region in the (x, y) plane. By integrating the joint PDF of X and Y over that region, the CDF of Z is found. The PDF can then be found by differentiating with respect to z. In principle, one can use this technique with any transformation; however, the integral to be computed may or may not be analytically tractable, depending on the specific joint PDF and the transformation.
To illustrate, consider a simple, yet very important example where the transformation is just the sum of the random variables, Z = X+Y. Then,
 (5.48)
(5.48)
Differentiating to form the PDF results in
![]() (5.49)
(5.49)
The last step in the previous equation is completed using Liebnitz’s rule*. An important special case results when X and Y are independent. In that case, the joint PDF factors into the product of the marginals producing
![]() (5.50)
(5.50)
Note that this integral is a convolution. Thus, the following important result has been proven:
Theorem 5.8: If X and Y are statistically independent random variables, then the PDF of Z = X + Y is given by the convolution of the PDFs of X and Y, fZ(z)=fX(z)*fY(z).
Example 5.20
Suppose X and Y are independent and both have exponential distributions,
![]()
The PDF of Z = X+Y is then found by performing the necessary convolution:

The above result is valid assuming that a ≠ b. If a = b, then the convolution works out to be
![]()
Students familiar with the study of signals and systems should recall that the convolution integral appears in the context of passing signals through linear time invariant systems. In that context, most students develop a healthy respect for the convolution and will realize that quite often the convolution can be a cumbersome operation. To avoid difficult convolutions, these problems can often by solved using a frequency domain approach in which a Fourier or Laplace transform is invoked to replace the convolution with a much simpler multiplication. In the context of probability, the characteristic function or the moment generating function can fulfill the same role. Instead of finding the PDF of Z = X+ Y directly via convolution, suppose we first find the characteristic function of Z:
![]() (5.51)
(5.51)
If X and Y are independent, then the expected value of the product of a function of X times a function of Y factors into the product of expected values:
![]() (5.52)
(5.52)
Once the characteristic function of Z is found, the PDF can be found using an inverse Fourier Transform.
Again, the characteristic function can be used to simplify the amount of computation involved in calculating PDFs of sums of independent random variables. Furthermore, we have also developed a new approach to find the PDFs of a general function of two random variables. Returning to a general transformation of the form Z = g(X, Y), one can first find the characteristic function of Z according to
![]() (5.53)
(5.53)
An inverse transform of this characteristic function will then produce the desired PDF. In some cases, this method will provide a simpler approach to the problem, while in other cases the direct method may be easier.
Example 5.21
Suppose X and Y are independent, zero-mean, unit-variance Gaussian random variables. The PDF of Z = X + Y2 can be found using either of the methods described thus far. Using characteristic functions,
![]()
The expected values are evaluated as follows:
![]()
The last step is accomplished using the normalization integral for Gaussian functions. The other expected value is identical to the first since X and Y have identical distributions. Hence,
![]()
The PDF is found from the inverse Fourier transform to be
![]()
The other approach is to find the CDF as follows:

Converting to polar coordinates,
![]()
Finally, differentiating with respect to z results in
![]()
Another approach to solving these types of problems uses conditional distributions. Consider a general transformation, Z = g(X, Y). Next, suppose we condition on one of the two variables, say X = x. Conditioned on X = x, Z = g(x, Y) is now a single variable transformation. Hence, the conditional PDF of Z given X can be found using the general techniques presented in Chapter 4. Once fZX (z x) is known, the desired (unconditional) PDF of Z can be found according to
![]() (5.54)
(5.54)
Example 5.22
Suppose X and Y are independent zero-mean, unit-variance Gaussian random variables and we want to find the PDF of Z = Y/X. Conditioned on X = x, the transformation Z = Y/x is a simple linear transformation and
![]()
Multiplying the conditional PDF by the marginal PDF of X and integrating out x gives the desired marginal PDF of Z.

Evaluating the integral in the last step can be accomplished by making the substitution u = (1 +z2)x2/2. Thus, the quotient of two independent Gaussian random variables follows a Cauchy distribution.
Up to this point, three methods have been developed for finding the PDF of Z = g(X, Y) given the joint PDF of X and Y. They can be summarized as follows:
• Method 1—CDF approach
Define a set R(z) = {(x, y): g(x, y) ≤ z}. The CDF of Z is the integral of the joint PDF of X and Y over the region R(z). The PDF is then found by differentiating the expression for the CDF:
 (5.55)
(5.55)
• Method 2—Characteristic function approach
First, find the characteristic function of Z according to:
![]() (5.56)
(5.56)
Then compute the inverse transform to get the PDF of Z.
• Method 3—Conditional PDF approach
Fix either X = x or Y = y (whichever is more convenient). The conditional PDF of Z can then be found using the techniques developed for single random variables in Chapter 4. Once the conditional PDF of Z is found, the unconditional PDF is given by
![]() (5.57)
(5.57)
Next, our attention moves to solving a slightly more general class of problems. Given two random variables X and Y, suppose we now create two new random variables W and Z according to some 2 × 2 transformation of the general form
 (5.58)
(5.58)
The most common example of this type of problem involves changing coordinate systems. Suppose, for example, the variables X and Y represent the random position of some object in Cartesian coordinates. In some problems, it may be easier to view the object in a polar coordinate system, in which case, two new variables R and Θ could be created to describe the location of the object in polar coordinates. Given the joint PDF of X and Y, how can we find the joint PDF of R and Θ?
The procedure for finding the joint PDF of Z and W for a general transformation of the form given in Equation (5.58) is an extension of the technique used for a 1 × 1 transformation. First, recall the definition of the joint PDF given in Equation (5.2) which says that for an infinitesimal region Ax, y = (x, x + εX ) x (y, y + εy ), the joint PDF, fx, y (x, y), has the interpretation
![]() (5.59)
(5.59)
Assume for now that the transformation is invertible. In that case, the transformation maps the region Ax, y into a corresponding region Az, w in the (z, w)-plane. Furthermore,
![]() (5.60)
(5.60)
Putting the two previous equations together results in
 (5.61)
(5.61)
A fundamental result of multi-variable calculus states that if a transformation of the form in Equation (5.58) maps an infinitesimal region Ax, y, to a region Az, w, then the ratio of the areas of these regions is given by the absolute value of the Jacobian of the transformation,
 (5.62)
(5.62)
The PDF of Z and W is then given by
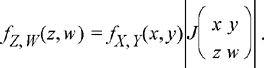 (5.63)
(5.63)
If it is more convenient to take derivatives of z and w with respect to x and y rather than vice-versa, we can alternatively use
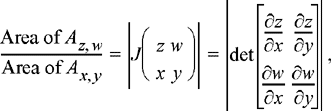 (5.64)
(5.64)
 (5.65)
(5.65)
Whether Equation (5.63) or (5.65) is used, any expressions involving x or y must be replaced with the corresponding functions of z and w. Let the inverse transformation of Equation (5.58) be written as
 (5.66)
(5.66)
Then these results can be summarized as
 (5.67)
(5.67)
If the original transformation is not invertible, then the inverse transformation may have multiple roots. In this case, as with transformations involving single random variables, the expression in Equation (5.67) must be evaluated at each root of the inverse transformation and the results summed together. This general procedure for transforming pairs of random variables is demonstrated next through a few examples.
Example 5.23
A classical example of this type of problem involves the transformation of two independent Gaussian random variables from cartesian to polar coordinates. Suppose
![]()
We seek the PDF of the polar magnitude and phase given by
![]()
The inverse transformation is
![]()
In this case, the inverse transformation takes on a simpler functional form and so we elect to use this form to compute the Jacobian.

The joint PDF of R and Θ is then

Note that in these calculations, we do not have to worry about taking the absolute value of the Jacobian since for this problem the Jacobian (= r) is always nonnegative. If we were interested, we could also find the marginal distributions of R and Θ to be
![]()
The magnitude follows a Rayleigh distribution while the phase is uniformly distributed over (0,2π).
Example 5.24
Suppose X and Y are independent and both uniformly distributed over (0,1), so that
![]()
Consider forming the two new random variables
![]()
The inverse transformation in this case is found to be

In this example, we compute the Jacobian by taking derivatives of z and w with respect to x and y to produce

Note that since x is always nonnegative, the absolute value of the Jacobian will just be 2π/x. The joint PDF of Z and W is then found to be

This transformation is known as the Box-Muller transformation. It transforms a pair of independent uniform random variables into a pair of independent Gaussian random variables. This transformation has application in the world of computer simulations. Techniques for generating uniform random variables are well known. This transformation then allows us to generate Gaussian random variables as well. More material on this subject is given in Chapter 12.
Example 5.25
Suppose X and Y are independent Gaussian random variables, both with zero-mean and unit variance. Two new random variables Z and W are formed through a linear transformation of the form
![]()
The inverse transformation is given by

With this general linear transformation, the various partial derivatives are trivial to compute and the resulting Jacobian is
![]()
Plugging these results into the general formula results in

With a little algebraic manipulation, it can be shown that this joint PDF fits the general form of a joint Gaussian PDF. In particular,

where ![]() and
and ![]()
A few remarks about the significance of the result of Example 5.25 are appropriate. First, we have performed an arbitrary linear transformation on a pair of independent Gaussian random variables and produced a new pair of Gaussian random variables (which are no longer independent). In the next chapter, it will be shown that a linear transformation of any number of jointly Gaussian random variables always produces jointly Gaussian random variables. Second, if we look at this problem in reverse, two correlated Gaussian random variables Z and W can be transformed into a pair of uncorrelated Gaussian random variables X and Y using an appropriate linear transformation. More information will be given on this topic in the next chapter as well.
5.10 Complex Random Variables
In engineering practice, it is common to work with quantities which are complex. Usually, a complex quantity is just a convenient shorthand notation for working with two real quantities. For example, a sinusoidal signal with amplitude, A, frequency, ω, and phase, θ, can be written as
![]() (5.68)
(5.68)
where j = ![]() The complex number Z = Aejθ is known as a phasor representation of the sinusoidal signal. It is a complex number with real part of X = Re[Z] = A cos (θ) and imaginary part of Y = Im[Z] = A sin (θ). The phasor Z can be constructed from two real quantities (either A and θ or X and Y).
The complex number Z = Aejθ is known as a phasor representation of the sinusoidal signal. It is a complex number with real part of X = Re[Z] = A cos (θ) and imaginary part of Y = Im[Z] = A sin (θ). The phasor Z can be constructed from two real quantities (either A and θ or X and Y).
Suppose a complex quantity we are studying is composed of two real quantities which happen to be random. For example, the sinusoidal signal above might have a random amplitude and/or a random phase. In either case, the complex number Z will also be random. Unfortunately, our formulation of random variables does not allow for complex quantities. When we began to describe a random variable via its CDF in the beginning of Chapter 3, the CDF was defined as FZz) = Pr(Z ≤ z). This definition makes no sense if Z is a complex number: what does it mean for a complex number to be less that another number? Nevertheless, the engineering literature is filled with complex random variables and their distributions.
The concept of a complex random variable can often be the source of great confusion to many students, but it does not have to be as long as we realize that a complex random variable is nothing more than a shorthand representation of two real random variables. To motivate the concept of a complex random variable, we use the most common example of a pair of independent, equal variance, jointly Gaussian random variables, X and Y. The joint PDF is of the form
 (5.69)
(5.69)
This joint PDF (of two real random variables) naturally lends itself to be written in terms of some complex variables. Define Z = X+jY, z = x + jy and μz = μ x +]μ y . Then,
 (5.70)
(5.70)
We reemphasize at this point that this is not to be interpreted as the PDF of a complex random variable (since such an interpretation would make no sense); rather, this is just a compact representation of the joint PDF of two real random variables. This density is known as the circular Gaussian density function (since the contours of fZ (z) = constant form circles in the complex z-plane).
Note that the PDF in Equation (5.70) has two parameters, μZ and σ. The parameter μZ is interpreted as the mean of the complex quantity, Z= X+ jY,
![]() (5.71)
(5.71)
But what about σ2? We would like to be able to interpret it as the variance of Z= X+ jY. To do so, we need to redefine what we mean by variance of a complex quantity. If we used the definition we are used to (for real quantities) we would find
![]() (5.72)
(5.72)
In the case of our independent Gaussian random variables, since Cov(X, Y) = 0 and Var(X) = Var(Y), this would lead to E [(Z – μZ )2] = 0. To overcome this inconsistency, we redefine the variance for a complex quantity as follows.
Definition 5.13: For a complex random quantity, Z = X+jY, the variance is defined as
![]() (5.73)
(5.73)
We emphasize at this point that this definition is somewhat arbitrary and was chosen so that the parameter σ2 which shows up in Equation (5.70) can be interpreted as the variance of Z. Many textbooks do not include the factor of 1/2 in the definition, while many others (besides this one) do include the 1/2. Hence, there seems to be no way to avoid a little bit of confusion here. The student just needs to be aware that there are two inconsistent definitions prevalent in the literature.
Definition 5.14: For two complex random variables Z1 = X1 + jY1 and Z2 = X2 + jY2, the correlation and covariance are defined as
![]() (5.74)
(5.74)
![]() (5.75)
(5.75)
As with real random variables, complex quantities are said to be orthogonal if their correlation is zero, whereas they are uncorrelated if their covariance is zero.
5.11 Engineering Application: Mutual Information, Channel Capacity, and Channel Coding
In Section 4.12, we introduced the idea of the entropy of a random variable which is a quantitative measure of how much randomness there is in a specific random variable. If the random variable represents the output of a source, the entropy tells us how much mathematical information there is in each source symbol. We can also construct similar quantities to describe the relationships between random variables. Consider two random variables X and Y that are statistically dependent upon one another. Each random variable has a certain entropy associated with it, H(X) and H(Y), respectively. Suppose it is observed that Y = y. Since X and Y are related, knowing Y will tell us something about X and hence the amount of randomness in X will be changed. This could be quantified using the concept of conditional entropy.
Definition 5.15: The conditional entropy of a discrete random variable X given knowledge of a particular realization of a related random variable Y= y is
 (5.76)
(5.76)
Averaging over all possible conditioning events produces
 (5.77)
(5.77)
The conditional entropy tells how much uncertainty remains in the random variable X after we observe the random variable Y. The amount of information provided about X by observing Y can be determined by forming the difference between the entropy in X before and after observing Y.
Definition 5.16: The mutual information between two discrete random variables X and Y is
 (5.78)
(5.78)
We leave it as an exercise for the reader to prove the following properties of mutual information:
Now we apply the concept of mutual information to a digital communication system. Suppose we have some digital communication system which takes digital symbols from some source (or from the output of a source encoder) and transmits them via some modulation format over some communications medium. At the receiver, a signal is received and processed and ultimately a decision is made as to what symbol(s) was most likely sent. We will not concern ourselves with the details of how the system operates, but rather we will model the entire process in a probabilistic sense. Let X represent the symbol to be sent, which is randomly drawn from some n-letter alphabet according to some distribution p = (p0, p1, …, pn –1). Furthermore, let Y represent the decision made by the receiver, with Y taken to be a random variable on an m-letter alphabet. It is not unusual to have m ≠ n, but in order to keep this discussion as simple as possible, we will only consider the case where m = n so that the input and output of our communication system are taken from the same alphabet. Also, we assume the system to be memoryless so that decisions made on one symbol are not affected by previous decisions nor do they affect future decisions. In that case, we can describe the operation of the digital communication system using a transition diagram as illustrated in Figure 5.7 for a three-letter alphabet. Mathematically, the operation of this communication system can be described by a matrix Q whose elements are qi, j = Pr(Y = i|X=j).

Figure 5.7 A transition diagram for a ternary (three-letter) communication channel.
We can now ask ourselves how much information does the communication system carry? Or, in other words, if we observe the output of the system, how much information does this give us about what was really sent? The mutual information answers this question. In terms of the channel (as described by Q) and the input (as described by p), the mutual information is
 (5.79)
(5.79)
Note that the amount of information carried by the system is a function not only of the channel but also of the source. As an extreme example, suppose the input distribution were p = (1, 0, …, 0). In that case it is easy to show that I(X, Y) = 0; that is, the communication system carries no information. This is not because the communication system is incapable of carrying information, but because what we are feeding into the system contains no information. To describe the information carrying capability of a communication channel, we need a quantity which is a function of the channel only and not of the input to the channel.
Definition 5.17: Given a discrete communications channel described by a transition probability matrix Q, the channel capacity is given by
 (5.80)
(5.80)
The maximization of the mutual information is with respect to any valid probability distribution p.
Example 5.26
As a simple example, consider the so-called binary symmetric channel (BSC) described by the transition probability matrix
![]()
The BSC is described by a single parameter q, which has the interpretation of the probability of bit error of the binary communications system. That is, q is the probability of the receiver deciding a 0 was sent when a 1 was actually sent and it is also the probability of the receiver deciding a 1 was sent when a 0 was actually sent. Since the input to this channel is binary, its distribution can also be described by a single parameter. That is, p = (p, 1–p). Likewise, the output of the channel is also binary and thus can be described in terms of a single parameter, r = (r, 1–r) where r= Pr (Y = 0) = p(1 – q) + q(1 – p). The mutual information for the BSC is
![]()
Some straightforward algebraic manipulations reveal that the above expression can be simplified to I(X; Y) = H (r)–H(q), where H(·) is the binary entropy function. Maximization with respect to p is now straightforward. The mutual information is maximized when the output distribution is r = (0.5,0.5) and the resulting capacity is
![]()
Due to the symmetry of the channel, the output distribution will be symmetric when the input distribution is also symmetric, p = (0.5,0.5). This function is illustrated in Figure 5.8.

Figure 5.8 Capacity of a binary symmetric channel.
The channel capacity provides a fundamental limitation on the amount of information that can reliably be sent over a channel. For example, suppose we wanted to transmit information across the BSC of Example 5.26. Furthermore, suppose the error probability of the channel was q = 0.1. Then the capacity is C = 1–H(0.1) = 0.53 bits. That is, every physical bit that is transmitted across the channel must contain less than 0.53 bits of mathematical information. This is achieved through the use of redundancy via channel coding. Consider the block diagram of the digital communication system in Figure 5.9. The binary source produces independent bits which are equally likely to be “0” or “1.” This source has an entropy of 1 bit/source symbol. Since the channel has a capacity of 0.53 bits, the information content of the source must be reduced before these symbols are sent across the channel. This is achieved by the channel coder which takes blocks of k information bits and maps them to n bit code words where n > k. Each code word contains k bits of information and so each coded bit contains k/n bits of mathematical information. By choosing the code rate, k/n, to be less than the channel capacity, C, we can assure that the information content of the symbols being input to the channel is no greater than the information carrying capability of the channel.
![]()
Figure 5.9 A functional block diagram of a digital communication system.
Viewed from a little more concrete perspective, the channel used to transmit physical bits has an error rate of 10%. The purpose of the channel code is to add redundancy to the data stream to provide the ability to correct the occasional errors caused by the channel. A fundamental result of information theory known as the channel coding theorem states that as k and n go to infinity in such a way that k/n ≤ C, it is possible to construct a channel code (along with the appropriate decoder) which will provide error-free communication. That is, the original information bits will be provided to the destination with arbitrarily small probability of error. The channel coding theorem does not tell us how to construct such a code, but significant progress has been made in recent years towards finding practical techniques to achieve what information theory promises is possible.
Exercises
Section 5.1: Joint CDFs
5.1 Recall the joint CDF given in Example 5.1,

5.2 A colleague of your proposes that a certain pair of random variables be modeled with a joint CDF of the form
![]()
(a) Find any restrictions on the constants a, b, and c needed for this to be a valid joint CDF.
(b) Find the marginal CDFs, FX (x) and Fy (y) under the restrictions found in part (a).
5.3 Consider again the joint CDF given in Exercise 5.2.
(a) For constants a and b, such that 0 ≤ a ≤ 1, 0 ≤ b ≤ 1 and a ≤ b, find Pr(a ≤ X ≤ b).
(b) For constants c and d, such that 0 ≤ c ≤ 1, 0 ≤ d ≤ 1 and c ≤ d, find Pr(c ≤ Y ≤ d).
(c) Find Pr(a ≤ X ≤ b|c ≤ Y≤d). Are the events {a ≤ X ≤ b} and {c ≤ Y ≤ d} statistically independent?
5.4 Suppose a random variable X has a CDF given by FX (x) and similarly, a random variable Y has a CDF, Fy (y). Prove that the function F(x, y) = FX (x)Fy (y) satisfies all the properties required of joint CDFs and hence will always be a valid joint CDF.
5.5 For the joint CDF that is the product of two marginal CDFs, FX, Y (x, y) = FX(x)FY (y), as described in Exercise 5.4, show that the events { a ≤ X ≤ b } and { c ≤ Y ≤ d } are always independent for any constants a ≤ b and c ≤ d.
Section 5.2: Joint PDFs
5.6 For positive constants a and b, a pair of random variables has a joint PDF specified by
![]()
5.7 For positive constants a, b,c, and positive integer n, a pair of random variables has a joint PDF specified by
![]()
5.8 A pair of random variables has a joint PDF specified by
![]()
(a) Find the constant d in terms of a, b, and c. Also, find any restrictions needed for a, b, and c themselves for this to be a valid PDF.
5.9 A pair of random variables has a joint PDF specified by

5.10 A pair of random variables has a joint PDF specified by
![]()
(b) Find Pr(0 ≤X≤ 2,|Y + 1| > 2).
(c) Find Pr(Y > X) Hint: Set up the appropriate double integral and then use the change of variables: u = x – y, v = x + y.
5.11 A pair of random variables, (X, Y), is equally likely to fall anywhere in the ellipse described by 9X2 + 4Y2 ≤ 36.
(a) Write the form of the joint PDF, fX, Y (x, y).
(b) Find the marginal PDFs, fX (x) and fy (y).
(c) Find Pr(X > 1) and Pr(Y ≤ 1)
(d) Find Pr(Y ≤ 1|X > 1). Are the events {X > 1} and { Y ≤ 1} independent?
5.12 A pair of random variables, (X, Y), is equally likely to fall anywhere within the region defined by |X| + |Y| ≤ 1.
Section 5.3: Joint PMFs
5.13 For some integer L and constant c, two discrete random variables have a joint PMF given by

5.14 Two discrete random variables have a joint PMF as described in the following table.

5.15 For a constant κ, two discrete random variables have a joint PMF given by

5.16 Let M be a random variable that follows a Poisson distribution, so that for some constant α, its PMF is
![]()
Let N be another random variable that, given M= m, is equally likely to take on any value in the set {0, 1, 2, …, m}.
Section 5.4: Conditional Distribution, Density and Mass Functions
5.17 For the discrete random variables whose joint PMF is described by the table in Exercise 5.14, find the following conditional PMFs:
5.18 Consider again the random variables in Exercise 5.11 that are uniformly distributed over an ellipse.
5.19 Recall the random variables of Exercise 5.12 that are uniformly distributed over the region |X| + |Y| ≤ 1.
(a) Find the conditional PDFs, fX|Y (x|y) and fY |X (y|x).
5.20 Suppose a pair of random variables (X, Y) is uniformly distributed over a rectangular region, A: x1
≤ X ≤ X2, y1 ≤ Y ≤ y2. Find the conditional PDF of (X, Y) given the conditioning event (X, Y) ε B, where the region B is an arbitrary region completely contained within the rectangle A as shown in the accompanying figure.

Section 5.5: Expected Values Involving Pairs of Random Variables
5.21 A pair of random variables has a joint PDF specified by

(a) Find the marginal PDFs, fX (x) and fY (y).
(b) Based on the results of part (a), find E[X], E[Y], Var(X), and Var(y).
(c) Find the conditional PDF, fX |Y (x|y).
(d) Based on the results of part (c), find E[XY], Cov(X, ν), and ρX, Y
5.22 A pair of random variables is uniformly distributed over the ellipse defined by x2 + 4y2 ≤ 1.
(a) Find the marginal PDFs, fX (x) and fY(y).
(b) Based on the results of part (a), find E[X], E[Y], Var(X), and Var(Y).
(c) Find the conditional PDFs, fX|Y (x|y) and fY |X (y|x).
(d) Based on the results of part (c), find E[XY], Cov(X, Y), and ρX, Y .
5.23 Prove that if two random variables are linearly related (i.e., Y = aX + b for constants a ≠ 0 and b), then

Also, prove that if two random variables have |ρ
X, Y
| = 1, then they are linearly related.
5.24 Prove the triangle inequality which states that
![]()
5.25 Two random variables X and Y have, μX =2, μY = –1, σ X = 1, σY = 4, and ρX,Y = 1/4. Let U = X +2Y and V = 2X – Y. Find the following quantities:
5.26 Suppose two random variables are related by Y = aX2 and assume that fX (x) is symmetric about the origin. Show that ρX, Y = 0.
5.27 Let X and Y be random variables with means μX and μY , variances σ2 X and σ2 Y , and correlation coefficient ρX, Y.
(a) Find the value of the constant a which minimizes [(Y – aX)2]
(b) Find the value of E[(Y – aX)2] when a is given as determined in part (a).
5.28 For the discrete random variables whose joint PMF is described by the table in Exercise 5.14, compute the following quantities:
5.29 Let Θ be a phase angle which is uniformly distributed over (0, 2π). Suppose we form two new random variables according to X = cos(aΘ) and Y = sin(aΘ) for some constant a.
(a) For what values of the constant a are the two random variables X and Y orthogonal?
(b) For what values of the constant a are the two random variables X and Y uncorrelated?
5.30 Suppose two random variables X and Y are both zero mean and unit variance. Furthermore, assume they have a correlation coefficient of ρ. Two new random variables are formed according to:

Determine under what conditions on the constants a, b, c, and d the random variables W and Z are uncorrelated.
Section 5.6: Independent Random Variables
5.31 Find an example (other than the one given in Example 5.15) of two random variables that are uncorrelated but not independent.
5.32 Determine whether or not each of the following pairs of random variables are independent:
(a) The random variables described in Exercise 5.6;
(b) The random variables described in Exercise 5.7;
(c) The random variables described in Exercise 5.14;
(d) The random variables described in Exercise 5.13.
5.33 Consider two discrete random variables X and Y which take on values from the set {1, 2, 3, …, k}. Suppose we construct an n × n matrix P whose elements comprise the joint PMF of the two random variables. That is, if pi, j is the element in the i th row and jth column of P, then pi, j = PX, Y (i, j) = Pr (X= i, Y=j).
(a) Show that if X and Y are independent random variables, then the matrix P can be written as an outer product of two vectors. What are the components of the outer product?
(b) Show that the converse is also true. That is, show that if P can be factored as an outer product, the two random variables are independent.
5.34 Two fair dice are rolled. Let one of the dice be red and the other green so that we can tell them apart. Let X be the sum of the two values shown on the dice and Y be the difference (red minus green) of the two values shown on the dice. Determine whether these two random variables are independent or not. Does you answer make sense?
Section 5.7: Joint Gaussian Random Variables
5.35 Starting from the general form of the joint Gaussian PDF in Equation (5.40), show that the resulting marginal PDFs are both Gaussian.
5.36 Starting from the general form of the joint Gaussian PDF in Equation (5.40) and using the results of Exercise 5.35, show that conditioned on Y = y, X is Gaussian with a mean of μX + ρXY (σX/σY ) (y – μY ) and a variance of σ2 X (1 – ρ2 XY ).
5.37 Two random variables are jointly Gaussian with means of μ X = 2, μY = –3, variances of σ2X = 1, σ2 Y = 4, and a covariance of Cov (X, Y) = –1.
(a) Write the form of the joint PDF of these jointly Gaussian random variables.
(b) Find the marginal PDFs, fX (x) and fY (y).
(c) Find Pr(X≤ 0) and Pr(Y > 0) and write both in terms of Q-functions.
5.38 Two random variables have a joint Gaussian PDF given by

5.39 Two random variables have a joint Gaussian PDF given by

Find E[X], E[Y], Var(X), Var(Y), ρX, Y , Cov(X, Y), and E[XY].
Section 5.8: Joint Characteristic and Related Functions
5.40 Let X and Y be zero-mean jointly Gaussian random variables with a correlation coefficient of ρ and unequal variances of σ2 X and σ2 Y .
(a) Find the joint characteristic function, ΦX, Y (ω1, ω2).
(b) Using the joint characteristic function, find the correlation, E[XY].
5.41 Find the general form of the joint characteristic function of two jointly Gaussian random variables.
5.42 A pair of random variables has a joint characteristic function given by
![]()
5.43 A pair of random variables has a joint characteristic function given by
![]()
(a) Find the joint PGF for the pair of discrete random variables given in Exercise 5.13.
5.45 A pair of discrete random variables has a PGF given by
![]()
5.46 The joint moment-generating function (MGF) for two random variables, X and Y, is defined as
![]()
Develop an equation to find the mixed moment E[XnYm
] from the joint MGF.
Section 5.9: Transformations of Pairs of Random Variables
5.48 A quarterback throws a football at a target marked out on the ground 40 yards from his position. Assume that the PDF for the football’s hitting the target is Gaussian within the plane of the target. Let the coordinates of the plane of the target be denoted by the x and y axes. Thus, the joint PDF of (X, Y) is a two-dimensional Gaussian PDF. The average location of the hits is at the origin of the target, and the standard deviation in each direction is the same and is denoted as σ. Assuming X and Y are independent, find the probability that the hits will be located within an annular ring of width dr located a distance r from the origin; that is, find the probability density function for hits as a function of the radius from the origin.
5.49 Let X and Y be independent and both exponentially distributed with
![]()
5.50 Let X and Y be jointly Gaussian random variables. Show that Z = aX + b Y is also a Gaussian random variable. Hence, any linear transformation of two Gaussian random variables produces a Gaussian random variable.
5.51 Let X and Y be jointly Gaussian random variables with E[X] = 1, E[Y] = – 2, Var(X) = 4, Var (Y) = 9, and ρ
X, Y
= 1/3. Find the PDF of Z = 2X – 3 Y – 5.
Hint: To simplify this problem, use the result of Exercise 5.50.
5.52 Let X and Y be independent Rayleigh random variables such that
![]()
5.53 Suppose X is a Rayleigh random variable and Y is an arcsine random variable, so that

Furthermore, assume X and Y are independent. Find the PDF of Z= XY.
5.54 Let X and Y be independent and both uniformly distributed over (0, 2π). Find the PDF of Z = (X + Y) mod 2π.
5.55 Let X be a Gaussian random variable and let Y be a Bernoulli random variable with Pr(Y=1) = p and Pr(Y=-1) = 1 – p. If X and Y are independent, find the PDF of Z= XY. Under what conditions is Z a Gaussian random variable?
5.56 Let X and Y be independent zero-mean, unit-variance Gaussian random variables. Consider forming the new random variable U, V according to
![]()
Note that this transformation produces a coordinate rotation through an angle of θ. Find the joint PDF of U and V. Hint: The result of Example 5.25 will be helpful here.
5.57 Let X and Y be zero-mean, unit-variance Gaussian random variables with correlation coefficient, ρ. Suppose we form two new random variables using a linear transformation:
![]()
Find constraints on the constants a, b, c, and d such that U and V are independent.
5.58 Suppose X and Y are independent and Gaussian with means of μX and μY, respectively, and equal variances of σ2. The polar variables are formed according to ![]() and Θ = tan−1 (Y/X).
and Θ = tan−1 (Y/X).
(a) Find the joint PDF of R and Θ.
(b) Show that the marginal PDF of R follows a Rician distribution.
5.59 Suppose X and Y are independent, zero-mean Gaussian random variables with variances of σ2X and σ2Y respectively. Find the joint PDF of
![]()
5.60 Suppose X and Y are independent, Cauchy random variables with PDFs specified by
![]()
Find the joint PDF of
![]()
5.61 Suppose M and N are independent discrete random variables. Find the PMF of L = M + N for each of the following cases:
(a) M and N both follow a uniform distribution,
![]()
(b) M and N follow different geometric distributions,

(c) M and N both follow the same geometric distribution,
![]()
5.62 Suppose M and N are independent discrete random variables with identical Poisson distributions,
![]()
Find the PMF of L= M – N. Hint: For this problem, you may find the series expansion for the modified Bessel function helpful:

Section 5.10: Complex Random Variables
5.63 A complex random variable is defined by Z = AejΘ, where A and Θ are independent and Θ is uniformly distributed over (0, 2π).
5.64 Suppose Z = X+jY is a circular Gaussian random variable whose PDF is described by Equation (5.70),

Find the characteristic function associated with this complex Gaussian random variable, ΦZ(ω) = E[exp(jωZ)]. Do you get the same (or different) results as with a real Gaussian random variable.
5.65 Suppose Z = X+jY is a circular Gaussian random variable whose PDF is described by Equation (5.70),

(a) Find the PDF of the magnitude, R =|Z|, and phase angle, Θ = ∠Z, for the special case when μz = 0.
(b) Find the PDF of the magnitude, R = Z, and phase angle, Θ = ∠Z, for the general case when μz ≠ 0. Hint: In this case, you will have to leave the PDF of the phase angle in terms of a Q-function.
(c) For the case when μz » σ, show that the PDF of the phase angle is well approximated by a Gaussian PDF. What is the variance of the Gaussian PDF that approximates the PDF of the phase angle?
Section 5.11: Mutual Information, Channel Capacity, and Channel Coding
5.66 Suppose  in Figure 5.7 and pi = 1/3, i = 1, 2, 3. Determine the mutual information for this channel.
in Figure 5.7 and pi = 1/3, i = 1, 2, 3. Determine the mutual information for this channel.
5.67 Repeat Exercise 5.66 if 
5.68 Repeat Exercise 5.66 if  Can you give an interpretation for your result.
Can you give an interpretation for your result.
5.69 Find the capacity of the channel described by the transition matrix,

5.70 For the transition matrix Q given in Exercise 5.66, prove that the equally likely source distribution, pi = 1/3, i = 1,2,3, is the one that maximizes mutual information and hence the mutual information found in Exercise 5.66 is the capacity associated with the channel described by Q.
Miscellaneous Problems
5.71 Suppose X and Y are independent and exponentially distributed both with unit-mean. Consider the roots of the quadratic equation z2+Xz +Y = 0.
(a) Find the probability that the roots are real.
5.72 In this problem, we revisit the light bulb problem of Exercises 3.43. Recall that there were two types of bulbs, long-life (L) and short-life (S) and we were given a box of unmarked bulbs and needed to identify which type of bulbs are in the box. In Exercise 3.43, we chose to run one of the bulbs until it burned out in order to help us identify which type of bulbs are in the box. This time, in order to obtain a more reliable decision, we are going to burn two different bulbs from the box, observe how long it takes each bulb to burn out, and then make a decision as to what type of bulbs are in the box. Let X represent the time that it takes the first bulb to burn out and let Y represent the time it takes the second bulb to burn out. It would seem reasonable to assume that X and Y are independent and since both bulbs are taken from the same box, the PDFs of there lifetimes should be the same. Modeling the conditional PDFs as in Exercise 3.43, we have

The a priori probability of the bulb types were Pr(S) = 0.75 and Pr(L) = 0.25.
(a) If the two bulbs are tested and it is observed that the first bulb burns out after 200 h and the second bulb burns out after 75 h, which type of bulb was most likely tested?
(b) What is the probability that your decision in part (b) was incorrect?
(c) Determine what decision should be made for each possible observation pair, {X= x, Y=y}. That is, divide the first quadrant of the (x, y)-plane into two regions, one including all sets of points for which we would decide that the bulbs are S-type and its complement where we decide the bulbs are L-type.
5.73 Once again, we will modify the light bulb problem of Exercise 5.72 in a manner similar to what was done in Exercise 3.44. Suppose we select two light bulbs to turn on when we leave the office for the weekend on Friday at 5 pm. On Monday morning at 8 am we will observe which of the light bulbs have burned out, if any. Let X be the lifetime of the first bulb and Y the lifetime of the second bulb. When we arrive at the office on Monday morning, there are four possible outcomes of the experiment:
(i) both bulbs burned out ⇔ {X ≤ 63 } ∩ { Y ≤ 63 },
(ii) the first bulb burned out while the second did not ⇔ {X ≤ 63 } ∩ { Y > 63 },
(iii) the second bulb burned out while the first did not ⇔ {X > 63 } ∩ { Y ≤ 63 },
(iv) neither bulb burned out ⇔ {X> 63} ∩ {Y > 63}.
For each of the four cases, determine what decision should be made regarding the type of bulbs that were in the box (i.e., L-type or S-type) and calculate the probability that the decision is wrong. As before, assume a priori probabilities of Pr(S) = 0.75 and Pr(L)= 0.25.
(a) Repeat Exercise 5.73 if we run the experiment over a 3-day weekend so that the experiment runs for 87 hours instead of 63.
(b) If we could choose the length of the experiment described in Exercise 5.73 to be anything we wanted, how long should we run the experiment in order to maximize our chances of correctly identifying the bulb type?
MATLAB Exercises
5.75 Provide contour plots for the ellipses discussed in Example 5.17. Consider the following cases:
Let c2 be the same for each case. Discuss the effect σX, σY and ρXY have on the shape of the contour. Now select one of the cases and let c2 increase and decrease. What is the significance of c2.
5.76 Let X and Y have a joint PDF given by
![]()
as in Example 5.6. Write a MATLAB program to generate many samples of this pair of random variables. Note that X and Y are independent, Gaussian random variables with unit variances and means of 2 and 3, respectively. After a large number of sample pairs have been generated, compute the relative frequency of the number of pairs that fall within the unit circle, X2+Y2 ≤ 1. Compare your answer with that obtained in Example 5.6. How many random samples must you generate in order to get a decent estimate of the probability?
5.77 Let X and Y have a joint PDF given by
![]()
5.78 Write a MATLAB program to evaluate Pr((X, Y ∈ ℜ)), where ℜ is the shaded region bounded by the lines y= x and y= – x as shown in the accompanying figure. You should set up the appropriate double integral and use MATLAB to evaluate the integral numerically. Note in this case that one of the limits of integration is infinit How will you deal with this?

5.79 Write a MATLAB program to generate pairs of random variables that are uniformly distributed over the ellipse x2 + 4y2 ≤ 1. Use the technique employed in Example 5.16. Also, create a three-dimensional plot of an estimate of the PDF obtained from the random data you generated.
* Liebnitz’s rule states that: ![]()

 (5.1e)
(5.1e) (5.8c)
(5.8c) (5.8d)
(5.8d) (5.8f)
(5.8f) (5.11b)
(5.11b)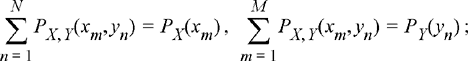 (5.11c)
(5.11c)