11 Basis theorems

In earlier chapters we have seen examples of uncountable sets of reals (e.g. and certain -sets) that contain perfect subsets. In this chapter we study basis theorems for uncountable sets of reals as well as basis properties of perfect sets.

11.1 A basis theorem for 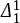-sets of reals

11.1.1 Friedman’s conjecture

Friedman [29] conjectured that every uncountable -set of reals has a member in each hyperdegree greater than or equal to the hyperdegree of . This conjecture was settled by Martin [94] and Friedman independently.

Theorem 11.1.1. (Martin [94] and Friedman). If A ⊆ ωω is an uncountable -set, then there is a perfect tree T ≤T such that [T]⊆ A and for any x ≥h , there is a z ∈ [T] with z ≡h x.

Suppose that A ⊆ ωω is an uncountable -set. By Corollary 2.2.14, there is a recursive function h : ωω → ωω and a -set B ⊆ ωω such that h maps B onto A and is injective on B. Then for every x ∈ B, h(x) ≡h x and for every y ∈ A, there exists an x ∈ B such that x ≡h h(x) = y. Hence it suffices to show that every x ≥h satisfies z ≡h x for some z ∈ B. Since B is a -class, there is a recursive tree T ⊆ ω<ω so that B =[T]= {x | (∀n) (x ↾ n ∈ T)}. We shall prove in the next section a slightly stronger result:

Theorem 11.1.2. Every -tree T1 with uncountably many infinite paths has a member in each hyperdegree greater than or equal to that of .

11.1.2 Proof of Friedman’s conjecture

We prove Theorem 11.1.2 following [172]. Let T1 ⊆ ω<ω be a -tree with a nonhyperarithmetic path. Then there is a enumeration of the nodes of ω<ω T1. We use T1[β] to denote the collection of nodes not yet enumerated up to stage β. Then Fix a nonempty recursive tree T0 ⊆ ω<ω having an infinite path and without a hyperarithmetic infinite path. Let f be the leftmost path of T0. Then f ≡h .

Lemma 11.1.3. If T1 ∩ [ν]= {τ ∈ T1 | τ ≻ ν} has no nonhyperarithmetic infinite path, then there is a stage β < ω1CK witnessing it. In other words, there is a partial function H : ω<ω → {0} such that H(σ) is undefined if and only if T1 ∩ [σ] contains a nonhyperarithmetic infinite path.

Proof. Suppose that σ ∈ T1 and T1 ∩ [σ] has no nonhyperarithmetic infinite path. We perform a Cantor–Bendixon type operation on T1 ∩ [σ] as follows: Let <KB be the Kleene–Brouwer ordering on ω<ω. At stage β < ω1CK, define a subtree T1β. T1β is in fact T1[β] except for the removal of those strings σ where [σ] is seen at stage β not to contain a nonhyperarithmetic path in T1.

Stage 0. Let T01 = T1[].

Stage β + 1. Given σ ∈ T1β and τ ≻ σ, if either

(1) there exists a <KB order-preserving function h : T1β ∩ [τ]→ β in Lβ (hence there is no infinite path in T1β ∩ [τ], or

(2) there exists a function h ∈ Lβ that enumerates T1β ∩ [τ] as a unique hyperarithmetic path.

Then let T1β+1 = T1β [τ] and declare that τ is removed from T1β at stage β + 1.

By the usual Cantor–Bendixon proof as in Proposition 3.6.10, if T1 ∩ [σ] has no nonhyperarithmetic infinite path, then every τ ≻ σ is removed at some stage β. Then by the admissibility of ω1CK, there is a stage βσ < ω1CK such that every τ ≻ σ is removed at βσ. At stage βσ, define H(σ) = 0.

Thus H may be viewed as a -partial enumeration function. A node σ ∈ ω<ω is a splitting node in the tree T1 if there exist i ≠ j such that both H(σ⌢i) and H(σ⌢j) are undefined. For a node σ ∈ ω<ω is a splitting node in the tree T1[β] if there exist i ≠ j such that both H(σ⌢i) and H(σ⌢j) are undefined at stage β. By a similar argument, there is a -partial function K : ω<ω → {0} such that K(σ) is undefined if and only if there exists an infinite path in T0 ∩ [σ]. Notethat K is different from H.

We call a node σ ∈ ω<ω a terminal node in T0 if K(σ) is defined. For β < ω1CK, σ ∈ ω<ω is a terminal node in T0[β] if K(σ) is defined at stage β.

Now for any x ≥h in 2ω, we builda z ∈ [T1] such that x ≡h z:

Stage 0. Let σ0 = .

Stage s + 1. Let σ' ≻ σs be the leftmost splitting node of T1 extending σs so that there are f(s) many splitting nodes between σs and σ'. Let σ'' ≻ σ' be the second leftmost splitting node extending σ' in T1. Set σs+1 ≻ σ'' to be the x(s)+ 1-th leftmost splitting node extending σ'' in T1.

Let z = ⋃s ∈ ω σs.

We prove that In fact we show that there is a (and hence -definable increasing sequence of ordinals {αs}s ∈ ω below ω1CK such that Then proving

The idea is to decode the construction of z in For each n < ω we use z to identify the value of f(n), where f is the leftmost path of T0. As an example, consider the case n = 0. Given β < ω1CK, we compute, beginning at the root of T1[β], the number lβ of times z “turns left” in T1[β]. Then lβ is a possible value of f(0). Of course this guess may be wrong. As an aid to making a better guess, we also determine if lβ is f(0) by asking if ⌢lβ is not a terminal node in T0[β] but ⌢l' is terminal for every l' < lβ. If this is not true, proceed to a stage β' > β where this holds. By the coding procedure, there must be a β' < ω1CK greater than β such that lβ'matches these requirements.

Let β1 be the first such stage. One is not able to conclude that lβ1 is indeed the real value of f(0). Both lβ1 and the computed value of f(0) (as seen in T0[β1])may change at a later stage. However, this situation does not occur infinitely often since otherwise either lβ goes to infinity or lβ = l infinitely often for some finite number l. In either case, since “σ is a terminal node in T1”isa Σ1-statement, z would be the leftmost path in T1, a contradiction. Hence incorrect guesses occur at most finitely many times and lβ reaches a limit after finitely many changes.

In general, to compute f(n) from z one imitates the guessing procedure for f(0). This will involve a finite injury argument. Thus once the finite sequence matches the computed values of f ↾ n at stage s, we set βs to be β. The sequence and values of f ↾ n computed at a later stage may change, but changes happen at most finitely often. Hence will reach a limit. Let γ be the least upper bound of {βs}s ∈ ω. Clearly γ < ω1z and the limit of {fβs }s ∈ ω is an infinite path in T0[γ]. Since [T0]=[T0[γ]], it is also an infinite path in T0. Moreover, it is the leftmost path. Hence z hyperarithmetically computes the leftmost path of T0.Using this, one shows by a decoding method that z ≡h x.

We now proceed with the formal proof.

Define αs, σsn, fs(n) as follows. The aim is to ensure that lims→ω fs(n) = f(n).

Stage 0. Let σ00 = and β0 = f0(n) = 0 for every n. We say that 0 receives attention.

Assume that at stage s ≥ 0, βs is defined and that if j ≤ s receives attention, then fs(j) and σsj are defined. Then z is said to be correct up to j at β if for every i ≤j, if 0 < i then

(1) fs ↾(i + 1) is the leftmost nonterminal node in T0[β];

(2) there exists a σ' ≺ σsi which is the leftmost splitting node of T1[β] so that σ' has fs(i)-many splitting nodes extending σsi−1 in T1[β], and

(3) for the σ' above, there is a node σ'' ≺ σsi extending σ' which is the second leftmost splitting node extending σ' in T1[β] so that σsi is the next splitting node extending σ'' in T1[β].

Stage s + 1. Let js+1 be the minimum of j ≤ s such that z is not correct up to j at βs + 1 if such a j exists, andletitbe s +1 otherwise. Initialize each j > js+1 and let fs+1(j) = fs(j) and σsj+1 = σsj for j < js+1. For j = js+1, there are two cases:

Case 1. js+1 has not received any attention since its last initialization, if any. Let be the next splitting node in T1[βs+1] and fs+1(js+1) = 0 and declare that js+1 receives attention at stage s + 1.

Case 2. Otherwise. Search for a β > βs less than ω1CK such that z is correct up to js+1 − 1 at β, and there exists a σ ≺ z extending for which there is an l satisfying

(i) fs ↾ js+1⌢(js+1, l) is the leftmost nonterminal node in T0[β];

(ii) there exists a σ' ≺ σ which is the leftmost splitting node of T1[β] such that σ' has l-many splitting nodes extending σsj−1 in T1[β], and

(iii) for the σ' above, there is a node σ'' ≺ σ extending σ' which is the second leftmost splitting node extending σ' in T1[β] so that σ is the next splitting node extending σ'' in T1[β].

Suppose that during the search in Case 2, z is always correct up to js+1 − 1. By the definition of z, a β as stipulated exists. Then let Declare that js+1 receives attention at stage s + 1.

Otherwise, z is not correct up to js+1 − 1 at β, and we replace js+1 by js+1 − 1 to do the search. However, this process of replacement occurs only finitely many times since z is always correct up to 0 at any β.

This completes the construction.

Let Then -sequence and hence γ < ω1z.

Lemma 1.1.4. For every j, there exists a stage sj such that if s ≥ sj then z is correct up to j at βs.

Proof. Suppose otherwise. Let j∗ be the least j such that for infinitely many s, z is not correct up to j∗ at βs. Then Case 2 in the construction applies to j∗. Let sj∗−1 be the least stage such that for every s ≥ sj ∗−1, z is correct up to j∗ − 1 at βs.

For s > sj ∗−1, let σ's be the σ' defined in the construction for j∗ at stage s. In other words, for some initial segment σ of z, σ's ≺ σ is the leftmost splitting node of T1[βs] such that σ's has fs(j∗)-many splitting nodes extending Note that for any Hence |σ's+1|≥|σ's| whenever s > sj∗−1. Since for any τ, z is not the leftmost path of T1 ∩ [τ], σj∗ = lims σ's exists. Let s1 > sj∗−1 be chosen such that σ's = σj∗ for s ≥ s1. By the construction, fs(j∗) = fs1(j∗) for s ≥ s1. It follows that there exists an sj∗ ≥ s1 such that for all s ≥ sj any s ≥ sj∗, z is correct up to j∗ at βs.

By Lemma 11.1.4, we may let Obviously, Note that for any So is an infinite path in T0. By the construction, = f and hence f ∈ Lγ+1[z]. Since f ≥h , we have ≤ h z and ω1CK < ωz1. Then the construction may be decoded from z. Thus z ≥h x. If x ≥h , then x may also decode the construction so that x ≡h z.

The construction in the proof above yields a perfect tree T ≤T with [T]⊆ A in which every infinite path x is hyperarithmetically above . This completes the proof of Theorem 11.1.2.

11.1.3 Exercises

Exercise 11.1.1. Prove that there is a -set A containing a real x ≥h byt not every hyperdegree above that of has a representative in A.

Exercise 11.1.2. (Feferman). Prove that there is a -set A in which any two distinct members are hyperarithmetically incomparable.

Exercise 11.1.3. Prove that if a -set A contains a member which hyperarithmetically computes every constructible real, then there is a cone of hyperdegrees in which every member has a representative in A.

Exercise 11.1.4. Prove that there is a perfect-set A ⊆ 2ω in which no member Turing computes '.

Exercise 11.1.5. Prove that the set {x ⊕ y | x ≤ h y} ⊆ 2ω is not Borel.

Exercise 11.1.6. (Kechris [64]). Prove that HYP is the largest -proper subset of 2ω which is closed under hyperarithmetic reducibility.

11.2 An antibasis theorem for -sets

11.2.1 An analysis of Theorem 11.1.1

A natural question arising from Theorem 11.1.1 is whether the condition x ≥h statement may be weakened to x(β) ≥T or even x(β) ≥T (β+1) for some β < ω1CK. The proof of the theorem requires at least ω1CK-many iterates of the Turing jump. A negative answer is given by Harrington:

Theorem 11.2.1. (Harrington [43]). For any ordinal β < ω1CK, there is an uncountable set A ⊆ ωω such that for each

We begin our discussion with the finite version of Theorem 11.2.1.

Theorem 11.2.2. There is an uncountable-set A ⊆ ωω such that for any x ∈ A and

Harrington’s proof uses an ingenious reverse induction construction. The following proof is more complicated than necessary, but the argument is applicable to a more general situation. By Theorem 2.1.4, the set H = {(i, (i)) | i < ω} ⊆ ω × 2ω is . Hence there is a recursive predicate P(i, σ, m) such that (i, x) ∈ H ⇔ (∀m)(∃k)P(i, x ↾ k, m). Let Tω ⊆ ω × ω<ω be a recursive tree such that

It is easy to verify that for each i < ω, there is a unique zi such that (i, zi) ∈ [Tω] and zi = (i) ⊕ yi for some yi ∈ ωω. Hence uniformly each (i) is a -singleton (in ωω).

We define three sequences of trees a sequence of functions {ψi}i<ω, and constants {cj}j ≤ 3 in ω such that for each i < ω,

Assume that these sequences have been defined.

Lemma 11.2.3. For each x ∈ and i < ω,

(i) x(i) ≡ x ⊕(i) and

(ii)

Proof. By (4), (5) and an induction on i, (i) is immediate. If x(i) ≥T (i+1), then x(i+1) ≡T x ⊕ (i+1) ≡T x(i), a contradiction. Hence (ii) holds.

Lemma 11.2.4. is homeomorphic to 2ω.

Proof. We define a bijection f between and 2ω as follows: For each x ∈ , let

Moreover, by (5b), for each i, |τn, n+i|≥ n+i. Let xn = ∪i∈ωτn, n+i. Then xn ∈ [Tn0] ∩ [y ↾ n]. Since ψ−1n is one-one, by (7) By the definition of f, we have f(x0) = y. So f is onto.

Now assume x0, x1 ∈ such that f(x0) = f(x1) and for some n0, and i ≠ j, x0 ↾ n0 = x1 ↾ n0, and x0 ≻ x0 ↾ n0⌢i, x1 ≻ x1 ↾ n0⌢j. By (5b) and (7), Then by (5a) and (5b), x0 ↾ n0 + 1 = x1 ↾ n0 + 1, a contradiction.

Clearly both f and f −1 are continuous. Thus [T0] is homeomorphic to 2ω.

Note that is a recursive tree. Hence the set A = [T0] is an uncountable -set with the desired property.

We turn now to defining the sequence of trees and functions as well as constants that satisfy (1)–(7). Given a tree T, write T = Φix if for any σ, σ ∈ T if and only if Φix(σ) = 1.

Lemma 11.2.5. There is a recursive function t : ω → ω such that for any x ∈ 2ω and tree is a tree in ω<ω and , where hx is an x-recursive function so that hx(〈e, n〉) is either 0 or min

Proof. Let

Then is as required. Since is obtained uniformly, we have a recursive function t : ω → ω such that = Φxt(i).

Now for i, j < ω such that we define a tree Ti such that Ti satisfies (1)–(7) upon substituting {cj}j ≤ 3 with parameters depending on Ti+1. The construction will be uniform in i and j. This means that there is a recursive function t such that By the Recursion Theorem, there is a c0 such that

The other parameters ci for 1 ≤ i ≤ 3 are obtained in the same way. Thus we may assume that has properties (1)–(7). Ti0 is defined from .

Lemma 11.2.6. Given a recursive tree T0 ⊆ ω<ω, there is a recursive tree T1 and a Δ02-homeomorphism ψ : T0 → T1 such that for any x ∈ [T1], x' ≡T x ⊕ '.

Proof. The proof is a finite injury argument. Given a recursive tree T0 ⊆ ω<ω, we define ψ and T1 by a full approximation construction.

Stage 0. Let ψ0() = and T1,0 = . We declare that all nodes σ ∈ T0 are fresh.

Stage s + 1. Suppose ψs : T0 → T1, s ⊆ 2≤s is partially defined. Search for the least t ≤ s withafresh σ ∈ 2t ∩ T0 for which there is a τ ∈ T1, s ∩ [ψs(σ)] ∩ 2≤s so that For each such σ, define ψs+1(σ) = τ' τ where |τ'|= τ⌢ s+1−t. For all ν’s in T0 ∩ Dom(ψs) which are incompatible with such σ’s, set ψs+1(ν) = ψs(ν). Define ψs+1(ν⌢i) = ψs(ν)⌢i if ν ∈ Dom(ψs) is incompatible with the σ’s and ν⌢i ∈ T0 Dom(ψs). Declarethat σ is not fresh for each such σ and τ is fresh for any τ extending such a σ. Let T1, s+1 = Range(ψs+1).

This completes the construction at stage s + 1. Note that for each σ, |{s | ψs(σ) ≠ ψs+1(σ)}| ≤ |σ|. Hence ψ(σ) = lims→∞ ψs(σ) exists for every σ. Then ψ is .

Let By the construction, ψ : [T0]→[T1] is a homeomorphism. Suppose x ∈ [T1]. Given t, todecideif Φtx(t) converges, we '-recursively search for a σ ∈ T1 ∩ 2t and a stage s ≥ t such that ψs(σ) = ψ(σ)≺ x. Then Φtx(t) is convergent if and only if Φψs(σ)t(t)[s]. Thus x' ≤T x ⊕ '.

Now for i < ω and σ ∈ 2i, let be a (i)-recursive tree as in Lemma 11.2.5 by setting T as and x as (i). Relativizing Lemma 11.2.6 to (i) by replacing T with ̂Ti+1, σ, we havea (i)-recursive homeomorphism where Ti, σ is T1 in Lemma 11.2.6. Define Ti0 to be a (i)-recursive tree so that τ ∈ Ti0 if and only if either

–|τ| ≤ i, or

–τ = (τ ↾ i)⌢τ' for some τ' ∈ Ti, τ↾i.

Define ψi ≤T (i+1) : such that

–if τ ∈ 2 ≤ i, then ψi(τ) = τ;

–otherwise, let τ =(τ ↾ i)⌢τ'. Define

Hence for any path x ∈ [Ti0],

Since the construction is uniform, it is straightforward to verify that (1)–(7) are satisfied. This completes the proof of Theorem 11.2.2.