2 Hyperarithmetic theory

In this chapter, we introduce the hyperarithmetic hierarchy and prove that the class of hyperarithmetic sets is precisely that of the -sets. Hence the hyperarithmetic hierarchy provides the right framework for analyzing and -sets. This equivalence also allows one to perform transfinite induction over -sets.

2.1 H-sets and -singletons

2.1.1 H-sets

Definition 2.1.1.

–The sequence is defined by transfinite induction over as follows.

–A member of is called an H-set. A real y is hyperarithmetic if y ≤T Hn for some n ∈ . We use HYP to denote the collection of all hyperarithmetic sets.

–Similarly, for any real x, the set is defined for all n ∈ :

Clearly n <o m implies Hn <T Hm. In fact,

Lemma 2.1.2 (Kleene). There is a recursive function f such that for all n, m, n <o m implies .

Proof. Let e0 be an index such that and let p, q be recursive functions such that implies and where 〈m, n〉 ∈ x. Fix a function g as in (i) of Theorem 1.3.4.

Define f by induction on <o. By the Recursion Theorem, we may assume that if n <o m then for all m′ <o m. If m = 2m′ for some m′ ∈ , then . If m = 3 ⋅ 5i for some i, then a recursive search for a pair (m′, k) such that m′ = Φi(k) and n ∈ Wg(m′) allows one to define .

Lemma 2.1.2 remains valid for relativized H-sets. Thus there is a recursive function f such that for all x, if n <ox m then .

2.1.2 -singletons

Let x be the unique real satisfying a predicate in the class Γ. Then x is said to be a Γ-singleton. We have seen that every -singleton is and is a -singleton. In this section we will show that every H-set is a -singleton.

Lemma 2.1.3. If x is a -singleton, then x′ and any y ≡T x is a -singleton.

Proof. Let x be a -singleton for the predicate R. Note that the set is for each e. Let e0 be an index such that for all y. Then the predicate

is . Note that x′ is the unique y such that Q(y) holds. If and then the predicate

is and witnesses the uniqueness of y.

Theorem 2.1.4. There exists a -predicate H such that for all reals y and ,

Hence every Hy-set is a (y)-singleton.

Proof. By the Recursion Theorem, we may assume that there exists a -predicate H(n, x, y) such that for each is defined and is the unique real y satisfying H(m′, y, x). If m = 2m′, by Lemma 2.1.3 we may define if and only if . If m = 3 ⋅ 5k for some k, then define if and only if .

We remark that the condition in Theorem 2.1.4 cannot be replaced by . It is not difficult to show that every -singleton in 2ω is recursive. On the other hand, every -singleton in 2ω is Turing reducible to a -singleton in ωω.

Proposition 2.1.5. If x ∈ 2ω is a -singleton, then there is a -singleton T ⊆ ωω whose unique member y is Turing equivalent to x.

Proof. Suppose that x ∈ 2ω is a -singleton. Then there is a recursive predicate R(n, σ) such that x is the unique real z satisfying (∀n)(∃m)R(n, z ↾ m). We may assume that (∀n)(∀σ)(R(n, σ) →|σ|≥ n). Let T be the set of y’s such that

–If y(n) = σ then R(n, σ);

–(∀τ ≺ y(n))(¬R(n, τ)), and

–.

Then T is a -set. Furthermore, if y ∈ T then for each n, y(n) is the shortest initial segment σ of x satisfying R(n, σ). Hence if y ∈ T, then ⋃n∈ω y(n) = x. It follows that y is the unique real in T.Clearly y ≡T x.

2.1.3 Exercise

Exercise 2.1.1. Prove that every -real x ∈ 2ω is a -singleton but there is a -real in 2ω which is not a -singleton.

2.2 -ness and hyperarithmeticity

In this section we prove the fundamental result that a set is if and only if it is hyperarithmetic.

2.2.1 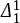-subsets of ω

Lemma 2.2.1. The following two predicates are :

Proof. Note that if and only if ∧(∀z)(H(n, z, y) → k ∈ z), and if and only if ∧(∀z)(H(n, z, y) → k ∉ z). By Proposition 1.2.5 and Theorem 2.1.4, both are .

Corollary 2.2.2 (Kleene [69]).

(i)If x is hyperarithmetic in y, then x is (y).

(ii)The set {(x, y) | x ∈ HYPy} is .

Proof. If x is hyperarithmetic in y, then there is an Hy-set such that x ≤T for some . Hence for some e. Then both the predicates

and

are (y) by Lemma 2.2.1.

Now where H is as in Theorem 2.1.4. Thus the set {(x, y) | x ∈ HYPy} is .

For each , define .

Lemma 2.2.3. The following predicates are :

Proof. By Theorem 1.3.4, define a -predicate P(x, y) to be the conjunction of the following three sentences:

and

Define a -set A = {〈m, n, y〉| (∀z)(P(z, y) → 〈m, n〉 ∈ z)}. It is easy to see that

The argument for (ii) is similar and is left as an exercise.

Lemma 2.2.4. There is a recursive function g such that for all .

Proof. We prove the unrelativized version. By the Recursion Theorem, we may assume that for all m <o n.

If n = 2m, define

where f is the function in (i) of Theorem 1.3.4. Note . If m ≠ 1 and m ∈ , then

Thus 2m may be computed by H2n via an oracle Turing machine whose index can be effectively obtained from g(m). Set the index to be g(n). Then .

If n = 3 ⋅ 5e, then

By Lemma 2.1.2, H2Φe(k) may be computed by Hn, and hence by H2n uniformly. Thus n is over Hn and so recursive in H2n. Moreover, the computation from H2n is uniform. Hence the index i of the oracle Turing machine computing n from H2n can be obtained effectively. Set g(n) = i. Then .

Corollary 2.2.5. If x is (y), then x is hyperarithmetic in y.

Proof. If x is (y), then there is recursive function f such that n ∈ x ⇔ f(n) ∈ y. The set A = {f(n) | n ∈ x} is (y). By Spector’s Boundedness Theorem (1.5.5), there is a number m ∈ y such that . Then . Hence by Lemma 2.2.4.

We have as a consequence the following characterization due to Kleene.

Theorem 2.2.6 (Kleene [69]). A real x is (y) if and only if it is hyperarithmetic in y.

The following corollary says that -sets are strongly reducible to H-sets.

Corollary 2.2.7. Every -real is many-one reducible to an H-set.

Proof. By Theorem 2.2.6, if x is then it is Turing reducible to Hn for some n ∈ .

Then x is many-one reducible to H2n =(Hn)′.

2.2.2 -sets of reals

There is a subtle point regarding uniformity when it comes to defining the notion of hyperarithmetic sets of reals. For this, we define ̂Hx-sets by induction on rather than on :

and

Definition 2.2.8. A set of reals A is hyperarithmetic if there is a number n ∈ and an index e such that for all .

Hence if A is hyperarithmetic, then there exist n and e such that

and

It follows that Lemma 2.2.1 remains true for such ̂Hx-sets and so A is .

Conversely, assume A is . According to the discussion in § 1.5.1, there are two numbers k0 and k1 such that x ∈ A ⇔ k0 ∈ ⇔ k1 ∉ . By relativizing Corollary 1.5.4, there is a recursive function p such that min{|k0|x, |k1|x}≤|p(k0, k1) |x for all x. Let n = 2p(k0, k1). Note that n ∈ for all x and so n ∈ = . Since Lemma 2.2.4 remains true, for all x. Hence there is a recursive function h such that for all n, giving . Thus we arrive at the following conclusion.

Theorem 2.2.9. A set of reals is hyperarithmetic if and only if it is .

Hyperarithmeticity also provides a scheme for inductive analysis of -sets of reals. We will show how this is implemented after introducing the ramified analytical hierarchy in § 3.8. The notion of a hyperarithmetic code, to be introduced in § 2.7, will also provide a powerful tool for the study of -sets of reals. The next proposition sets an effective bound on |n|x if n ∈ for all x.

Proposition 2.2.10. If n ∈ for all x, then there is a recursive ordinal β such that |n|x < β for all x.

Proof. If not, m ∈ WF0 ⇔ (∃f)(∃x)(∀i)(∀j)(Rm(i, j) → 〈f(i), f(j)〉 ∈ ) where g is the recursive function in (ii) of Theorem 1.3.4. So WF0 is , a contradiction.

It also follows from the discussion above that = if and only if every y ≤h x is recursive in for some n ∈ .

2.2.3 Parametrization of 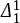-sets

As a first application of the results above, we demonstrate a parametrization of -reals.

Proposition 2.2.11. There is a partial function D : ω × ω → ω with a -graph GD such that for all x, x ∈ ⇔ (∃m)(∀i)(∀j)(x(i) = j ↔(m, i, j) ∈ D).

Proof. Define D = {(〈n, e〉, i, j) |n ∈ ∧ is total ∧ (i) = j}. By Theorem 2.2.6, for all x, x ∈ ⇔ (∃m)(∀i)(∀j)(x(i) = j ↔(m, i, j) ∈ D)).Moreover, (〈n, e〉, i, j) ∈ D ⇔ n ∈ ∧(∀z)(H(n, z)∧ is total → (i) = j), where H is as defined in § 2.1.2. Hence GD is .

Proposition 2.2.11 may be applied to reduce certain -predicates to .

Corollary 2.2.12. For any -predicate P(x, y), the predicate Q(y) ⇔ (∃x ∈ )(P(x, y)) is .

Proof. By Proposition 2.2.11, Q(y) ⇔ (∃x ∈ )P(x, y) is equivalent to

Note that for each m, if (∀i)(∃j)((m, i, j) ∈ D), then the predicate (m, i, j) ∈ D is . Hence Q is .

One may relativize the above proposition to the statement “for any -predicate P(x, y), the predicate Q(y) ⇔ (∃x ∈ (y))P(x, y) is ”, which is used to derive a classical result in descriptive set theory:

Corollary 2.2.13. If the function f : ωω → ωω is and one-one, then f(A) is for any -set A.

Proof. If f is and total, by Proposition 1.1.8, Gf is . Hence f −1({y}) is (y) for any y. Since f is one-one, by Proposition 1.1.15, the unique real f −1(y) is (y). So y ∈ f(A) ⇔ (∃x ∈ (y))(y ∈ A ∧(x, y) ∈ Gf) ⇔ (∃x)(x ∈ A ∧(x, y) ∈ Gf). By relativizing Corollary 2.2.12 to y, one concludes that f(A) is .

Thus we obtain a characterization of -sets of reals:

Corollary 2.2.14. A set of reals A is if and only if there is a -set B and a recursive function f : ωω → ωω such that f(B) = A and f is one-one on B.

Proof. If there is a -set B and a one-one recursive function f : ωω → ωω such that f(B) = A, then, by Corollary 2.2.13, one easily verifies that A is .

If A ⊂ ωω is , then there is a recursive function g such that x ∈ A ⇔ g(x) ∈ WO1 and, by the discussion in § 1.5.2, there is a recursive well-ordering z such that x ∈ A ⇔|g(x) | ≤ |z|. Define P(x, y) if and only if y is an isomorphism from ≤g(x) to an initial segment of ≤z. Since z is recursive, P(x, y) is and x ∈ A ⇔ (∃!y)P(x, y). Hence there is a recursive predicate R such that P(x, y) ⇔ (∀n)(∃m)R(x, y, n, m). Uniformize P by defining a -set B = {x0 ⊕ x1 ⊕ x2 | (∀n)(R(x1, x2, n, x0(n)) ∧ (∀m < x0(n))¬R(x1, x2, n, m))}. Define a recursive function f such that f(x) = x1 if x = x0 ⊕ x1 ⊕ x2.Obviously f is one-one on B.

In certain situations, Corollary 2.2.14 enables one to reduce a construction over a -set to one that is over a -set. Additionally, Theorem 2.2.9 provides a parametrization of -sets of reals.

Proposition 2.2.15. There is a -set A ⊆ ω × ωω with the property that for any set B of reals, B is if and only if there is an n such that B = An = {x | (n, x) ∈ A}.

Proof. Define . By Theorem 2.2.9, A is as required.

2.2.4 Exercises

Exercise 2.2.1. Complete the proof of Lemma 2.2.3.

Exercise 2.2.2. Prove that for any n ∈ , there exists an uncountable -set P ⊆ 2ω in which every real recursive in Hn is recursive.

Exercise 2.2.3. Prove that there is a B ⊆ such that <o is a well-ordering on B of order type .

2.3 Spector’s Uniqueness Theorem

Since the H-sets are generated by a -singleton process (cf. Theorem 2.1.4), they provide a way of carrying out transfinite induction over hyperarithmetic sets. We make this observation precise by noting Corollary 2.3.2, the Spector Uniqueness Theorem, which implies that induction over H-sets is degree-theoretic invariant.

Theorem 2.3.1 (Spector [153]). There is a recursive function h such that

Proof. We prove this by induction on the well-ordering < of 2:

There are four cases to consider.

(1) n = 1. Set h(1, m) = c1 so that for all x.

(2) n = 2i ∧ m = 2j. Fix a recursive function g so that for any e, x and y, x = implies . Set h(n, m) = g(h(i, j)).

(3) n = 3 ⋅ 5k. Set h(n, m) = c3 so that is the characteristic function of {〈i, j〉| .

(4) n = 2k ∧ m = 3 ⋅ 5l. This is the most difficult case. By Lemma 2.2.4, we may Hm-recursively search for an i such that and . By Lemma 2.1.2, there is a recursive function f so that . By induction, Hn = . Then there exists a c4 with . Set h(n, m) = c4.

Note that these cases can be identified recursively. Hence h is a recursive function.

Thus we have the following uniqueness theorem.

Corollary 2.3.2 (Spector). If n, m ∈ , then |n| = |m| implies Hn ≡T Hm.

In particular, for any recursive ordinal β, the“β-th Turing jump”, denoted (β), may be taken to be Hn for any n ∈ with |n| = β. There is a parallel result for ̂Hx-sets with exactly the same proof as that of Theorem 2.3.1. We leave it to the reader as an exercise.

Theorem 2.3.3. There is a recursive function h such that for any real x,

2.3.1 Exercise

Exercise 2.3.1. Prove Theorem 2.3.3.

2.4 Hyperarithmetic reducibility

2.4.1 -reducibility

Definition 2.4.1. x y if x is (y). In particular, x ≤h y if x y.

Proposition 2.4.2 (Shoenfield). If x y and y z, then x z.

Proof. If x y, then there is a -predicate R such that n ∈ x ⇔ R(n, y).

If y z, then there is a -predicate S such that n ∈ y ⇔ S(n, z).

Then

Thus x z.

Reals x, y are said to have the same -degree if x y and y x. If n = 1, then we also say that they have the same hyperdegree. By Theorem 2.2.6, x ≤h y if and only if there is an n ∈ and an e such that . The hyperjump of x is defined to be the set .

The h-reduction relation x ≤h y suggests another reason for introducing the ̂Hx-sets. One of the problems with h-reducibility is that, unlike the case of Turing reducibility where one examines a fixed recursive list of possible reduction algorithms (independently of the sets x and y being considered), there is no uniform procedure to search for an algorithm that h-reduces x to y. The reduction depends on what can be Turing computed by the Hy-sets and this involves ordinal notations for y. Different reals y have different ordinal notations. In certain cases the notations may be markedly different since is unbounded in ω1. The use of ̂Hy-sets circumvents this difficulty. If , then the sets Turing computable by the ̂Hy-sets are precisely the (y)-sets. Hence while it is not true in general, for reals y with ,one does have a uniform reduction.

2.4.2 The partial order of hyperdegrees

The Turing jump operator is order preserving on the Turing degrees. This remains true for the hyperjump operator which preserves order on the hyperdegrees.

Proposition 2.4.3. x ≤h y ⇔ ≤m .

Proof. First of all is (x). If x ≤h y, then as in the proof of Proposition 2.4.2 is (y). By Theorem 1.5.1, ≤m .

If ≤m , then x ≤m ≤m . So x is (y). Since ωx is (x), ω x ≤m ω−x ≤m ≤m . Then ω x is (y) and this implies that x ≤h y.

One of the most basic theorems in classical recursion theory is the Friedberg–Mučnik Theorem ([28] and [109]) which asserts the existence of two incomparable r.e. Turing degrees. Since -sets are seen as analogs of r.e. sets in the higher setting, the following result shows that there is a fundamental difference between the two notions of reducibility.

Theorem 2.4.4 (Spector [153]). If x, y ∈ and y ∉ HYP, then x ≤h y.

Proof. We show that ≤h y. By Theorem 1.5.1, there is a recursive function f such that n ∈ y ⇔ f(n) ∈ . Since y ∉ HYP, by Lemma 2.2.4, sup{|f(n) |n ∈ y} is . Then

and

By Lemma 2.2.3, ≤h y.

Remark 2.4.5. Theorem 2.4.4 prompted Kreisel to suggest that h-reduction was not the “correct” notion of reducibility for higher recursion theory. This led to the introduction of the notion of metarecursive reducibility in metarecursion theory. It is shown in Sacks [118] that there exist two -sets with incomparable metadegrees.

There is a tight link between and the h-degree of x, as illustrated in the following proposition:

Proposition 2.4.6 (Spector [153]). .

Proof. Since x ≤h y, every x-recursive well-ordering relation R ⊆ ω2 is in y. By relativizing Proposition 1.5.6 to y, R has order type < . Hence ≤ .

The converse of Proposition 2.4.6 does not hold in general. However, there is an important partial result which characterizes .

Theorem 2.4.7 (Sacks). > if and only if x ≥h .

We decompose the proof into two lemmas, with the following left as an exercise:

Lemma 2.4.8 (Sacks). Suppose x ≤T y. Then there is a recursive function f such that

(i)(∀n)(∀m)(n <ox m → f(n) <oy f(m)),

(ii)(∀n)(n ∈ →|n|x = |f(n) |y).

Lemma 2.4.9 (Spector [153]).

Proof. (i) <ox is (x) and hence is recursive in . Thus by Proposition 2.4.6, < .

(ii) If x ≤h y, then x ≤T for some n ∈ . Let f be as in Lemma 2.4.8. Since < , by Proposition 2.4.6, . Hence there is a number such that for all i, . Thus .

Proof of Theorem 2.4.7. If , then by (ii) of Lemma 2.4.9, ≤h x.

If ≤h x, then by (i) of Lemma 2.4.9, < .

The following corollary says that each h-degree not above the hyperjump is GL1. This is in sharp contrast to Turing reducibility where there exist reals such that :

Corollary 2.4.10. .

Proof. If ≤h x ⊕ , then x <h ≤h x ⊕ . Hence x ≱h . Conversely, if x ≱h , then by Theorem 2.4.7, . By (ii) of Lemma 2.4.9, ≤h x ⊕ .

Corollary 2.4.11. The set {x | = } is .

Proof. By Proposition 1.2.5, is a -singleton. Then x ≥h if and only if (∃n ∈ , which is a -statement. By Theorem 2.4.7, the set {x | = } is .

2.4.3 Exercises

Exercise 2.4.1. Prove Lemma 2.4.8.

Exercise 2.4.2. Prove that the set {x | = } is ().

2.5 Some basis theorems and their applications

2.5.1 Gandy’s Basis Theorem

A set of reals A is a basis for a collection of sets P of reals if for any nonempty P ∈ P, P ∩ A ≠ . Basis theorems are very important in recursion theory. They are used among other things to pin down the complexity of predicates. For example, let {Ti}i<ω be an effective enumeration of recursive trees in 2<ω. The index set N = {i | Ti contains an infinite path} appears to be . But one can show that every recursive tree in 2<ω containing an infinite path must contain an infinite path recursive in ′ (see Exercise 1.5.3). So N is an arithmetical set.

Lemma 2.5.1. Suppose that T ⊆ ω<ω is a recursive tree with an infinite path. There is an infinite path x ∈ [T] recursive in .

Proof. Suppose that T ⊆ ω<ω is a recursive tree with an infinite path. Note that the set S = {σ ∈ T | (∃y ≻ σ)(∀n)(y ↾ n ∈ T)} ⊆ T is a nonempty -tree without dead ends and so recursive in . Since T has an infinite path, so does S. Hence, the leftmost infinite path x in S is recursive in .

Thus the collection of reals recursive in is a basis for recursive trees in ω<ω, while the set of hyperarithmetic reals is not:

Proposition 2.5.2. There is a recursive tree S ⊆ ω<ω with uncountably many infinite paths but without a hyperarithmetic infinite path.

Proof. By Corollary 2.2.2, the set A of non-hyperarithmetic reals is . Then there is a recursive tree T ⊆ 2<ω × ω<ω such that for any x ∈ 2ω, x ∈ A if and only if there exists a y satisfying (∀n)((x ↾ n, y ↾ n) ∈ T). Let S ⊆ ω<ω be a recursive tree such that σ ∈ S if and only if (σ0, σ1) ∈ T where σ0(n) = σ(2n) and σ1(n) = σ(2n + 1) for all n which makes sense for the σi’s. Then for any infinite path x ∈ [S], x = x0 ⊕ x1 so that x0 ∈ A. In other words, every infinite path in S Turing computes a nonhyperarithmetic real. Moreover, by the definition of A, every nonhyperarithmetic real is recursive in an infinite path in S. Hence S contains uncountably many infinite paths.

Theorem 2.5.3 (Gandy [33]). If A is and nonempty, then A contains a real x such that ωx1 = and x ≤T .

Proof. By Corollary 2.2.2, the set B = {x ⊕ y | y ≰h x ∧ x ∈ A} is also a nonempty set. By Lemma 2.5.1, there is a real x ⊕ y ∈ B and x ⊕ y ≤T . Hence x ∈ A is recursive in . Since y ≤h x, we have x ≱h . By Theorem 2.4.7, = .

Theorem 2.5.3 is known as the Gandy Basis Theorem.