Lemma 14.3.6. If x is -random and y ≤h x, then there is a recursive ordinal γ such that y ≤T x ⊕(γ).

Proof. Since x is -random, we have = . Let y ≤h x. Then there is a formula with rank at most β0 < such that

By Lemma 13.1.1, there is a recursive ordinal β > β0 such that

is recursive in (β). By Lemma 13.1.10, there is a recursive ordinal β1 ≥ β such that for any number i and formula ψ with rank β, there is a formula ψ′ with rank at most β1 such that {z | (, z) ψ′} is a ((β1)-subset of {z | (, z) ψ} with difference in measure less than 2−i. Note that the search procedure for β1 from β0 is effective in In this way one obtains a Δ1-sequence of ordinals β0 < β1 < … in Let . Then for any β < γ,

(i) the set

is recursive in (γ), and

(ii) for any number i and formula ψ with rank β, there is a formula ψ′ with rank less than γ so that {z | (, z) ψ′} is a ((β′))-subset of {z | (, z) ψ} for some β′ < γ with difference in measure less than 2−i.

Note that for any ranked formula ψ, if x ∈ Pψ = {z | (, z) ψ}, then Pψ has positive measure.

Since x is -dominated, there is a hyperarithmetic function f : ω → ω such that for any e and n ∈ with |n| < γ such that computes a tree Te,n, if x [Te,n] then .

Now recursively in x ⊕ (γ) ⊕ f , search for a formula ψ0 with rank less than γ such that S0 = {z | (, z) ψ0} contains x, has positive measure, and is a closed subset of either {z | (, z) φ(z, Ō)} or {z | (, z) ¬φ(z, Ō)}. Since x is -random, by (ii) there is such a ψ0. Note that one needs x ⊕(γ) ⊕f to decide if x ∈ S0. Inductively, for each n, search recursively in x⊕0(γ) ⊕f for a formula ψn+1 with rank less than γ such that Sn+1 = {z | (, z) ψn+1} contains x, has positive measure, and is a closed subset of either or . Since x is -random, by (ii), such a ψn+1 exists. This implies that y ≤T x ⊕(γ) ⊕ f

Since f is hyperarithmetic, there is a γ0 < such that f ≤T ( γ0). Without loss of generality, assume γ0 ≤ γ (replacing γ with γ+ γ0 if necessary). Then y ≤T x ⊕(γ) .

Corollary 14.3.7. If x is -random and y ≤h x, then there is a recursive ordinal β, a function f ≤T (β) and a recursive functional Ψ such that for every n, y(n) = Ψx⊕0(β)↾f(n)(n)[f(n)].

Proof. Suppose that x is -random and y ≤h x. By Lemma 14.3.6, there is a recursive ordinal γ and a recursive function Φ such that for every n, y(n) = Φx⊕0(γ)(n). Let g <h x be a function such that for every n, y(n) = Φx⊕0(γ)↾g(n)(n)[g(n)]. Since x is -dominated, there is a hyperarithmetic function h so that for all n, h(n)> g(n).

Hence there is a sufficiently large recursive ordinal β such that both x and h are many-one reducible to (β). It Is not difficult to define a function f ≤T (β) and a recursive function Ψ so that for every n, y(n) = Ψx⊕0(β)↾f(n)(n)[f(n)].

Theorem 14.3.8. If x is -random and y ≤h x is not hyperarithmetic, then there is a -random z ≡h y.

Proof. Suppose x is -random and y ≤h x is not hyperarithmetic. By Corollary 14.3.7, there is a recursive ordinal β, a nondecreasing function f ≤T (β) and a recursive function Ψ such that limn→∞ f(n) = ∞ and for every n,

For each u ∈ 2<ω, let

and

where τ < u means, as strings, τ is to the left of u.

One may view as a “measure” for τ. For each n, let

Then ln ≤ ln+1 ≤ rn+1 ≤ rn. Since y is not hyperarithmetic, it is not difficult to see that limn→∞ rn = 0. Hence there is a unique

Clearly z ≤T y ⊕(β). We leave it to the reader to verify that y ≤T z ⊕(β). Thus z ≡h y.

Suppose that z is not -random. Then there is a recursive ordinal γ < β and a (γ)-ML-test {Vn}n∈ω such that . Let

Intuitively, {̂Vn}n<ω is a -Martin-Löf test relative to the measure λ, where λ(σ) = ∑τ∈C(σ) 2−|τ| for any σ ∈ 2<ω.

Since z ∈ Vn, we have y ∈ ̂Vn for every n. Note that {̂Vn}n<ω is (γ+1+β)-r. e.

Let

Then {Un}n<ω is (γ+1+β)-r. e and . Note that for every n,

Then {Un+1}n<ω is a (γ+1+β)-ML-test. Hence x is not a -random, a contradiction.

14.3.4 Exercises

Exercise 14.3.1 (Hjorth and Nies [51]). Prove that x ⊕ y is -random if and only if x is -random and y is (x)-random.

Exercise 14.3.2 (Yu [171]). For any z ≥h , there is a -random x ≡h z which is not -ML random.

Exercise 14.3.3. Prove that if x is -random, then for any -set A of reals containing x,

Exercise 14.3.4. Prove that there is a -set A and a -ML random x ∈ A such that .

Exercise 14.3.5. Prove that every x HYP hyperarithmetically reducible to a -random real is -random relative to a continuous measure.

Exercise 14.3.6 (Kjos-Hanssen and Yu). Let Φ be a universal partial -function from ω to 2, and assume that x(e) ≠ Φ(e, e) for each e. Show that x hyperarithmetically computes some member of a given nonempty -closed subset of 2ω.

Exercise 14.3.7 (Greenberg, Montalbán and Slaman [39]; Kalimullin and Nies). Suppose that M is a structure such that the set A = {x |(∃ ≤T x)( ≅ )} has measure 1. Prove that every -random real is in A.

Exercise 14.3.8 (Kripke [120]). If A is a nullset of hyperdegrees such that , then the set is also null.

14.4 and -randomness

14.4.1 -randomness

Since there is a -real which is -random, -randomness is strictly stronger than -randomness. By Corollary 13.1.7 and Proposition 13.1.12, we have the following conclusion.

Proposition 14.4.1. Assume that < ω1. Then -randomness = -ML randomness = -randomness.

14.4.2 -ML randomness

Let {φn(σ)}n<ω be a recursive enumeration of -formulas. There is a Σ1-formula ψ(n, σ) (in set theory) such that

Let (n, σ)∈ U if and only if

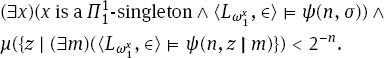
One may view (n, σ) ∈ U as an enumeration of strings σ in U up to any stage coded by a -singleton where the measure is less than 2−n. We leave it to the reader to verify that U is . Then the set {Un}n<ω, where Un = {σ |(n, σ)∈ U}, is a universal -ML-test.

Hence there is a -closed set P which contains only -ML random reals. It follows that the leftmost path in P is -equivalent to a -real and so belongs to L.

By Proposition 4.4.6, every x ∈ P ∩ L satisfies > . This applies in particular to the leftmost path x in P. Hence if one stays within L, the situation that one normally sees in standard randomness theory no longer applies. Note that by applying a method similar to that in the proof of Theorem 14.2.10, one may separate -ML randomness from -randomness.

Proposition 14.4.2. If V = L, then every nonzero -degree contains a -ML random real.

Proof. First observe that the set P above can be presented by a -tree T. By Proposition 4.4.6, T is in every x ∈[T] and T has the least nontrivial -degree. Hence the proposition follows.

14.4.3 -randomness

Definition 14.4.3. We say that x is L-random if for any Martin-Löf test {Un}n<ω in L,

L-randomness was essentially introduced by Solovay [150]. The following fact is immediate.

Proposition 14.4.4. The followings are equivalent:

(i)x is L-random;

(ii)x does not belong to any Borel nullset coded in L;

(iii)x is ℝ = 〈T, ≤〉-generic over L, where ℝ is the notion of random forcing as defined in § 6.2.2.

Proof. Obviously (iii) ⇒ (ii) ⇔ (i). By Proposition 6.2.6, ℝ is c. c. c. Then it follows that for any dense subset , is a Borel co-nullset with a Borel code in L. Hence (ii) ⇒ (iii).

Theorem 14.4.5 (Solovay [150]). If the set of L-random reals has measure 1, then every -set is measurable.

Proof. Suppose that A is a -set of reals defined by a formula φ(x) in the language of set theory so that

Let be a maximal antichain in L so that for any p ∈ , p ⊩ φ(). Then is countable. Let . Then R is a Borel set with a Borel code in L. If x is L-random, then x is an ℝ-generic real over L. Hence if x is L-random in R, then 〈L[x], ∈〉 φ(x) and so x belongs to A. Note that ′ = {r |(∃p ∈ )(r ≤ p)∨(∀p)(∀q)(p ∈ ∧ q ≤ p → q r)} is a dense set. Thus if x ∈ A, then x ∈ R so that for any L-random real x, x ∈ A if and only if x ∈ R. Since the set of L-random reals has measure 1, A is equal to R modulo a nullset. It follows that A is measurable.

Theorem 14.4.6 (Stern [161]). For any real x, x is -random and = if and only if x is L-random.

Proof. Let x be -random such that = . If x is not L-random, then let

be a nonempty (x)-set. Then there is an r x so that x ∈ , a contradiction.

Conversely, let x be L-random. Then x is -random. Suppose that > . Then there are -formulas φ(x, m, n) and ψ(x, m, n) defining an r ∈ L coding a well-ordering greater than . By Corollary 4.2.9, . By (iii) in Proposition 14.4.4, there is a condition p ∈ T ∩ L such that

Then for any L-random real z ∈ p, r z. Applying Levy collapse over V, in V[G] the set of L-random reals is of measure 1. It follows that in V[G], the set

has positive measure. By Theorem 14.4.5 and Proposition 13.1.9, r is in V[G] and so in V, a contradiction.

Note that the set of L-random reals is . Thus if the measure of non-L-random reals is 0, then every -random real is L-random.

Theorem 14.4.7 (Stern [161]). Assume that the set of L-random reals has measure 1. Then the set of non-L-random reals is the largest null -set and so -randomness is equivalent to L-randomness.

Proof. For a contradiction, suppose that A is a null -set containing an L-random real x. Then there is a formula φ defining A such that 〈L[x], ∈〉 φ(x). By Proposition 14.4.4, there is a condition p ∈ T ∩ L such that p ⊩ φ(). Hence for any random real y ∈ p, we have 〈L[y], ∈〉 φ(y). Thus φ(y) holds for any y ∈ p. Since the set of L-random reals has measure 1, it follows that μ(A) > 0, a contradiction.

Hence if (ω1)L < ω1, then -randomness is strictly stronger than -ML randomness. Indeed, the conclusion is provable in ZFC.

Proposition 14.4.8. There is a -ML random real which is not -random.

Proof. Let T ⊆ 2<ω be a -tree containing only -ML random reals. Then by a method similar to that used in the proof of Lemma 14.2.12, replacing with , one is able to show that the leftmost path of T is covered by a -nullset. We leave it to the reader to fill in the details.

One may also introduce the notion of strong -ML randomness by considering reals that avoid all generalized -ML tests. Then Proposition 14.4.8 says that strong -ML randomness is different from -ML randomness. Note that every generalized -ML test {Un}n<ω is a member of L, and by Corollary 13.1.7, 〈L, ∈〉 μ(∩n<ωUn) = 0. Hence there is a real in L which is strongly -ML random. It follows that if the set of constructible reals is null, then strong -ML randomness is strictly weaker than -randomness.

14.4.4 Exercises

Exercise 14.4.1. Separate -ML randomness from -randomness.

Exercise 14.4.2. Every -set is measurable if and only if almost every real is L-random.

Exercise 14.4.3. Assume V = L. Prove that there is no largest -nullset.

Exercise 14.4.4. Complete the proof of Proposition 14.4.8.

Exercise 14.4.5 (Stern [161]). Prove that it is consistent with ZFC that (ω1)L = ω1 and almost every real is L-random.

Exercise 14.4.6. Assume V = L. Show that every nontrivial -degree contains a strongly -ML random real.

Exercise 14.4.7. Let r be random over L. Show that in L[r], there is no real which is Cohen generic over L.

Exercise 14.4.8. Let g be Cohen generic over L. Show that in L[g], the set of constructible reals is null but no real is L-random.

14.5 Kolmogorov complexity and randomness

14.5.1 The Kolmogorov complexity of -random reals

Proposition 14.5.1. The following are equivalent:

(i)x is -random.

(ii)For any z ∈ HYP which is Martin-Löf random,

(iii)For any z ∈ HYP which is Martin-Löf random,

Proof. (i) ⇔ (ii). By Proposition 14.2.2, x is -random if and only if for any hyperarithmetic z, x is Martin-Löf random relativized to z. By Theorem 12.1.10, this is equivalent to stating that for any hyperarithmetic Martin-Löf random z, x is Martin-Löf random relativized to z. By van Lambalgen’s Theorem 12.1.7, this is in turn equivalent to saying that for every hyperarithmetic Martin-Löf random z, x ⊕ z is Martin-Löf random which, by Theorem 12.2.11, is equivalent to “for any hyperarithmetic Martin-Löf random z, (∃c)(∀n)(K(x ↾ n)≥ 2n − C(z ↾ n)− c)”.

One proves similarly that (i) ⇔ (iii).

Corollary 14.5.2. -randomness is upward closed for both K- and C-degrees.

14.5.2 The Kolmogorov complexity of -random reals

Proposition 14.5.3. For any -random x, if either x ≤K y or x ≤C y, then y is -random.

Proof. Suppose that x is -random and x ≤K y (resp. x ≤C y). By Corollary 14.5.2, y is -random. Note that {z | x ≤K z} (resp. {z | x ≤C z}) is (x). By Theorem 12.2.14 and Lemma 2.5.4 relativized to x, y ≤h x and so = . Then by Corollary 14.3.2, y is -random.

One may also show that -randomness is both K-and C-upward closed. By Theorem 14.4.7, if (ω1)L < ω1, then -randomness is upward closed for both ≤K and ≤C. It is not known if -ML randomness is upward closed for either of these reducibilities.

14.5.3 Exercise

Exercise 14.5.1. Prove that there is no function f such that x is -random if and only if (∃c)(∀n)(K(x ↾ n)≥ n + f(n)− c).

14.6 Lowness for randomness

Lowness notions for higher randomness generally parallel those for randomness over the natural numbers. In this section, we omit proofs about lowness properties which are minor modifications of those for the latter. The reader is referred to the relevant books or papers for details.

14.6.1 Lowness for higher Kurtz randomness

Lemma 14.6.1. If x is -dominated and -semitraceable, then x is low for -Kurtz tests.

Proof. Suppose x is -dominated and -semitraceable. Let U be a (x) open set with measure 1. Then there is a y ≤h x such that U is (y). Let Φ be a Turing reduction so that the domain of Φy is U. Write Uz for the domain of Φz for any z. Note that U = Uy.

Define a (x) function ̂f by: ̂f (n) is the shortest string σ ≺ y with μ(Uσ[σ]) > 1 − 2−n. By the hypothesis of the theorem, there is an increasing -function g and a -function f such that for every n, there is an m ∈[g(n), g(n + 1)) with f(m) = ̂f(m). Without loss of generality, we may assume that μ(Uf(m)[m]) > 1 − 2−m for every m.

Define a -open set V such that σ ∈ V if and only if there exists an n so that . By the property of f and g, V ⊆ Uy = U. But for every n,

Hence

This implies that x is low for -Kurtz tests.

Lemma 14.6.2. If x is low for -Kurtz randomness, then x is -dominated.

Proof. We first show that if x is low for -Kurtz tests, then x is -dominated.

Suppose f ≤h x is an increasing function. Let Sf = {z | (∀n)(z(f(n)) = 0)}. Obviously Sf is a (x)-closed nullset. Hence there is a -closed nullset [T] ⊇ Sf where T ⊆ 2<ω is a -tree. Define

Since μ([T]) = 0, g is . We claim that g dominates f .

For every n, Sf(n) = {σ ∈ 2f(n) | (∀i ≤ n)(σ(f(i)) = 0)} has cardinality 2f(n)−n. However, if g(n)≤ f(n) then applying S ⊆ [T] one has

This is a contradiction. Hence x is -dominated.

Now suppose x is not -dominated witnessed by an f ≤h x. Then Sf is not contained in any -closed nullset. Indeed it is not difficult to see that for any σ with [σ]∩ Sf ≠ 0, [σ]∩ Sf is not contained in any -closed nullset (otherwise, as proved above, one shows that f is dominated by a -function). Then by induction, one constructs a -Kurtz random z ∈ Sf as follows:

Let P0, P1, … be an enumeration of the -closed nullsets. First choose the least τ such that [τ]∩ Sf ≠ 0 but [τ]∩ Sf ∩ P0 = 0. Let l0 = |τ| and z ↾ l0 = τ. Suppose that at stage n + 1, z ↾ ln is defined so that [z]↾ ln] ∩ Sf ≠ ≠. Then there is τ ≻ z ↾ ln such that [τ] ∩ Sf ≠ but [τ] ∩ Sf ∩ Pn = . Choose the least such τ and let ln+1 = |τ| and z ↾ ln+1 = τ. Then z ∈ Sf is -Kurtz random. Thus x is not low for -Kurtz randomness.

The proof of the following lemma is left to the reader.

Lemma 14.6.3 (Kučera [76]). Suppose T ⊆ 2<ω and P ⊆ ω<ω are -trees with μ([T]) > 0. Then there is a -tree S ⊆ T and a constant c such that for any e, if [Pe] ⊆ S is not empty, then μ([Pe]) > 2−e−c, where Pe = {σ |(e, σ) ∈ P}.

The following lemma is essentially due to Joseph Miller.

Lemma 14.6.4. For any non--semitraceable real x and -tree T ⊆ 2<ω with μ([T]) > 0, there exist z ∈[T] and y ≤h x such that y ⊆ z and |{n | y(n) = 1}| = ℵ0.

Proof. Let x be non--semitraceable and let T ⊆ 2<ω be a -tree with μ(T)> 2−k for some k > 0. By Lemma 13.3.10, there is a function f ≤h x such that for any partial -function p : ω × 2<ω → ω, there are at most finitely many (n, σ)’s satisfying f(n, σ) = p(n, σ).

Let P ⊆ ω × 2<ω be a universal -tree, i. e. P is a -tree and for any -tree Q ⊆ 2<ω, there is an e such that Pe = Q. We may assume that there is a recursive function h such that for any 〈e0, e1〉, Ph(〈e0,e1〉) = Pe0 ∩ Pe1.

Let S ⊆ T be as in Lemma 14.6.3. Let S = Pe0 for some e0. We may also assume that there is a recursive function g : 2<ω → ω such that Pg(σ) = {τ | τ ∈ Pe0 ∧(∀n)(σ(n) = 1 → τ(n) = 1)}. For σ ∈ 2<ω, let

Then the set {(σ, Aσ)| σ ∈ 2<ω} is a -set. Moreover, if [Pg(σ)] ≠ 0, then

Thus |A|≤ h(i(σ)) + c. It follows that there is a partial -function p : ω × 2<ω → ω such that for any n, if p(n, σ) = k then

–k ∈ Aσ, and

–(∀m < n)(∃k′)(k′ ≠ k ∧ p(m, σ) = k′).

Hence {p(n, σ)}n≤h(i(σ))+c is a one-one enumeration of Aσ. Note that

Hyperarithmetically in x compute a k such that k ∉ Aσ and k > |σ| as follows. Fix a recursive bijection q : ω → ω<ω. We may assume that f(n, σ) ≠ q(p(n, σ))(n) for all n and σ. Define g1 :2<ω → ω<ω hyperarithmetically in x such that g1(σ) is a finite string in ωh(i(σ))+c and

Hence if [Pi(σ)] ≠ , then g1(σ) ≠ p(n, σ) for all n ≤ h(i(σ)). For such a σ, q−1(g1(σ)) ≠ p(n,σ) for all n. Thus q−1(g1(σ)) ∉ Aσ and so Without loss of generality, we may assume that q−1(g1(σ))>|σ|.

Using q−1 ∘ g1, starting with σ0 = , hyperarithmetically in x construct a sequence σ0 ≺ σ1 ≺ … of strings such that for each n,

– and

–σn+1 = σn ∪{q−1(g1(σn))}.

Hence and for any , the real is a subset of z.

Corollary 14.6.5. If x is not -semitraceable, then x is not low for -Kurtz randomness.

Proof. Suppose that x is not -semitraceable. Let T be a -tree so that μ([T]) > 0 and [T] contains only -ML random reals. Then by Lemma 14.6.4, there is a z ∈[T] and a y ≤h x such that z is a member of the (x)-closed nullset {r | y ⊆ r}. Hence x is not low for -Kurtz randomness.

This leads us to the following theorem.

Theorem 14.6.6 (Kjos-Hanssen, Nies, Stephan and Yu [68]). For any x ∈ 2ω, the following are equivalent:

(i)x is low for -Kurtz tests;

(ii)x is low for -Kurtz randomness;

(iii)x is -dominated and -semitraceable.

It is not known if there exists a nonhyperarithmetic real which is low for -Kurtz randomness. However, we can prove the following set inclusion.

Proposition 14.6.7 (Kjos-Hanssen, Nies, Stephan and Yu [68]). If x is low for -Kurtz randomness, then x is low for -Kurtz randomness.

Proof. Assume that x is low for -Kurtz randomness, y is -Kurtz random and there is a (x)-closed nullset A with y ∈ A. By Proposition 14.1.2, the set

is a -nullset. Then A B is (x). Since y is -Kurtz random, y ∉ B. Hence y ∈ A B and so A B is (x) and nonempty. Thus there is a z ∈ A B with ωz1 = = . Since z ∉ B, z is -Kurtz random. By Proposition 14.1.4, z is -Kurtz random. This contradicts the fact that x is low for -Kurtz randomness.