Chapter 14
Pricing by Arbitrage
Pricing by arbitrage means that an asset is priced with the unique arbitrage-free price. Pricing by arbitrage can be applied in two different settings: (1) We can price by arbitrage linear securities, like forwards and futures, in any markets. (2) We can price by arbitrage nonlinear securities, like options, in complete markets. We discuss both of these cases in this chapter.
If two assets have the same terminal value with probability one, then the assets should have the same price. Otherwise, we could obtain a risk-free profit by selling the more expensive asset and by buying the cheaper asset. Linear assets, like futures, can be defined as a linear function of the underlying assets. Thus, they can be replicated, and their price is the initial value of the replicating portfolio. Nonlinear assets, like options, can be replicated only under restrictive assumptions on the markets (under the assumption of complete markets). However, the restrictive assumptions are often not too far away from the real properties of the markets.
The concepts of an arbitrage-free market and a complete market were studied in Chapter 13. The results of Chapter 13 imply that if the market is arbitrage-free and complete, then there is only one arbitrage-free price. In fact, Theorem 13.2 states that the arbitrage-free prices are obtained as expected values with respect to the equivalent martingale measures, and Theorem 13.3 (the second fundamental theorem of asset pricing) states that if the market is arbitrage-free and complete, then there is only one equivalent martingale measure.
Section 14.1 discusses pricing of futures, the put–call parity, and the American call options.
Section 14.2 studies binary models. In these models the price of a stock can at any time move only one step up, or one step down. The binary models are complete models, thus a derivative has a unique arbitrage-free price. These prices can be easily computed. The prices are called the Cox–Ross–Rubinstein prices, and they were introduced in Cox et al. (1979).
Section 14.2.3 studies asymptotics of multiperiod binary models, as the number of periods increases, and the length of the periods decreases. A multiperiod binary model converges to a log-normal model. In the log-normal model the stock price follows a geometric Brownian motion. The geometric Brownian motion is a market model that does not exactly describe the actual markets but it can be rather close to the actual markets. The Black–Scholes prices are obtained as the limits of the Cox–Ross–Rubinstein prices. The derivation of the Black–Scholes prices from the Cox–Ross–Rubinstein prices is both elegant and it leads to efficient numerical recipes, although there are many other derivations of the Black–Scholes price (see Section 14.3.3).
Section 14.3 studies the properties of the Black–Scholes prices. Section 14.4 studies Black–Scholes hedging. Section 14.5 studies combining the Black–Scholes hedging with time changing volatility estimates. This method of option pricing provides a benchmark against which we can evaluate competing pricing and hedging methods.
14.1 Futures and the Put–Call Parity
Futures can be priced by arbitrage regardless whether the market is complete or not. The payoff of a futures contract is a linear function of the underlying, and thus a futures contract can be replicated even in an incomplete market. The put–call parity provides a related example of pricing by arbitrage, which works whether the market is complete or not: the payoff of a put subtracted from the payoff of a call is a linear function of the underlying.
14.1.1 Futures
We consider pricing of stock futures, currency forwards, forward zero-coupon bonds, and forward rate agreements.
14.1.1.1 Stock Futures
A futures contract on a stock is made at time ![]() . The contract specifies that the buyer of the contract has to buy the stock at a later time
. The contract specifies that the buyer of the contract has to buy the stock at a later time ![]() with price
with price ![]() . We assume that the stock does not pay dividends during the time period from
. We assume that the stock does not pay dividends during the time period from ![]() to
to ![]() . Let us denote with
. Let us denote with ![]() the price of the stock at time
the price of the stock at time ![]() . The value of the futures contract at the expiration time
. The value of the futures contract at the expiration time ![]() is
is
because the buyer of the futures contract gives away ![]() and receives
and receives ![]() .
.
The price of a zero-coupon bond is taken as ![]() , where
, where ![]() ,
, ![]() is the annualized risk-free rate, and
is the annualized risk-free rate, and ![]() is the time between
is the time between ![]() and
and ![]() in fractions of a year. This is the method of continuous compounding.1
in fractions of a year. This is the method of continuous compounding.1
What is the fair value ![]() of the futures contract for
of the futures contract for ![]() ? We may replicate the futures contract buy buying the stock and borrowing the amount
? We may replicate the futures contract buy buying the stock and borrowing the amount ![]() . At time
. At time ![]() the value of this portfolio is
the value of this portfolio is
with probability one. At time ![]() the value of this portfolio is
the value of this portfolio is ![]() with probability one. Thus,
with probability one. Thus,
for ![]() , by the law of one price, to exclude arbitrage.
, by the law of one price, to exclude arbitrage.
When an investor enters a futures contract in a futures exchange, this does not imply any cash flows, although the exchange requires from the investor a liquid collateral in order to secure a possible future payment. The fair forward price is called such value of ![]() that makes the value
that makes the value ![]() of the futures contract zero. To get
of the futures contract zero. To get ![]() we need that
we need that
The future prices that are quoted in a futures exchange are the values ![]() (which are determined by the supply and demand). Numbers
(which are determined by the supply and demand). Numbers ![]() are called futures prices or forward prices.
are called futures prices or forward prices.
A buyer of a stock future or a stock index future saves the carrying costs but looses the possible stock dividends. When the annualized dividend rate is known to be ![]() , then the fair future price is
, then the fair future price is
14.1.1.2 Currency Forwards
A currency forward is made at time ![]() . We denote with
. We denote with ![]() the exchange rate USD/euro at time
the exchange rate USD/euro at time ![]() . Let
. Let ![]() be an exchange rate. The contract stipulates that the buyer will buy
be an exchange rate. The contract stipulates that the buyer will buy ![]() US dollars with euros at time
US dollars with euros at time ![]() , using the USD/euro exchange rate
, using the USD/euro exchange rate ![]() . The value of the contract for the buyer at time
. The value of the contract for the buyer at time ![]() is
is
Indeed, the buyer uses ![]() euros to buy
euros to buy ![]() dollars. Then the buyer exchanges the dollars to euros to obtain
dollars. Then the buyer exchanges the dollars to euros to obtain ![]() euros. The profit of the buyer is
euros. The profit of the buyer is ![]() .
.
What is the price ![]() of the currency forward for
of the currency forward for ![]() ? We can replicate the currency forward using zero-coupon bonds. Let
? We can replicate the currency forward using zero-coupon bonds. Let ![]() be the USD price of the US zero-coupon bond and let
be the USD price of the US zero-coupon bond and let ![]() be the euro price of an European zero-coupon bond. The zero-coupon bonds are such that
be the euro price of an European zero-coupon bond. The zero-coupon bonds are such that ![]() USD and
USD and ![]() . Let us consider the portfolio with
. Let us consider the portfolio with ![]() units of US zero-coupon bonds and with
units of US zero-coupon bonds and with ![]() units of European zero-coupon bonds. The value of the portfolio at time
units of European zero-coupon bonds. The value of the portfolio at time ![]() is
is
We choose
The value of the portfolio a time ![]() is
is
Since (14.3) and (14.4) are equal, the portfolio replicates the currency forward, and the price ![]() of the currency forward is equal to
of the currency forward is equal to ![]() at time
at time ![]() .
.
The price is in euros
To make ![]() we need to choose the exchange rate
we need to choose the exchange rate

14.1.1.3 Forward Zero-Coupon Bonds
A time ![]() two parties make an agreement to exchange at a future time
two parties make an agreement to exchange at a future time ![]() a zero-coupon bond whose maturity is at
a zero-coupon bond whose maturity is at ![]() , with a cash payment
, with a cash payment ![]() . At time
. At time ![]() only the agreement is made, and at time
only the agreement is made, and at time ![]() the cash payment is made and the zero-coupon bond is received. This is called a forward zero-coupon bond. Forward zero-coupon bonds are considered in Section 18.2.1.
the cash payment is made and the zero-coupon bond is received. This is called a forward zero-coupon bond. Forward zero-coupon bonds are considered in Section 18.2.1.
Let ![]() be the price of the forward zero-coupon bond. Let
be the price of the forward zero-coupon bond. Let ![]() and
and ![]() be the prices of zero-coupon bonds with maturities
be the prices of zero-coupon bonds with maturities ![]() and
and ![]() . Then,
. Then,
Consider a portfolio with one unit of ![]() and short of
and short of ![]() units of
units of ![]() . The portfolio has value
. The portfolio has value
for ![]() . Thus,
. Thus, ![]() and we have replicated the forward zero-coupon bond. Thus, at time
and we have replicated the forward zero-coupon bond. Thus, at time ![]() the prices are equal:
the prices are equal:
To make ![]() , we need to choose the cash payment
, we need to choose the cash payment ![]() as
as

14.1.1.4 Forward Rate Agreements
A forward rate agreement allows to change a floating Libor rate against a fixed rate. The contract is made at time ![]() . The reset time of the Libor is
. The reset time of the Libor is ![]() . At this time the Libor rate is settled to be
. At this time the Libor rate is settled to be ![]() , where
, where ![]() is the maturity of the Libor. The agreement stipulates that the buyer of the contract pays the payment with the fixed rate
is the maturity of the Libor. The agreement stipulates that the buyer of the contract pays the payment with the fixed rate ![]() , and receives the payment with the Libor rate
, and receives the payment with the Libor rate ![]() . Thus, the payoff for the buyer at time
. Thus, the payoff for the buyer at time ![]() is
is
where ![]() is the notional, and
is the notional, and ![]() is the time between
is the time between ![]() and
and ![]() . Forward rate agreements are considered in Section 18.2.2.
. Forward rate agreements are considered in Section 18.2.2.
Let ![]() and
and ![]() be zero-coupon bonds. The forward rate agreement can be replicated by the trading strategy
be zero-coupon bonds. The forward rate agreement can be replicated by the trading strategy
where ![]() is the strategy of buying
is the strategy of buying ![]() and reinvesting the payoff at time
and reinvesting the payoff at time ![]() with the prevailing
with the prevailing ![]() -period Libor rate. Thus, the payoff of
-period Libor rate. Thus, the payoff of ![]() at time
at time ![]() is equal to
is equal to ![]() . Thus, the trading strategy gives the payoff (14.6). The present value of the forward rate agreement is equal to
. Thus, the trading strategy gives the payoff (14.6). The present value of the forward rate agreement is equal to
To make ![]() , we need to choose
, we need to choose

14.1.1.5 Backwardation and Contango
Backwardation refers to the price relation where the spot price is higher than the forward price and contango refers to the case where the spot price is lower than the forward price:

At the expiration, the spot price and the futures price should be equal (to prevent arbitrage). Thus, the contango relationship means that distant delivery months trade at a greater price than near-term delivery months (the term structure is upward-sloping). Depending on the type of the underlying, either the contango or the backwardation is typical.
In the case of stock futures, or stock index futures, the theoretically fair price of a futures contract is greater than the spot price, according to (14.2). Thus, contango is typical for stock futures. However, futures prices ![]() can differ from the theoretically fair price, and thus both contango and backwardation are possible. In the case of stock futures we can change the terminology in the following way:
can differ from the theoretically fair price, and thus both contango and backwardation are possible. In the case of stock futures we can change the terminology in the following way:

According to this terminology we do not compare futures prices to the spot prices but to the theoretically fair prices.2
When the underlying is a commodity, then there are borrowing costs for the seller of the futures contract, similarly as in the case of stock futures. In addition, there are costs for storing the commodity, for the seller of the futures contract. Thus, contango is typical for futures on commodities, and contango is typically more profound than for stock futures.
The buyer of a treasury bond future saves carrying costs (determined by the short-term rate) but looses the interest received by the bond owners (determined by the long-term rate). If the short-term rate is significantly less than the long-term rate, then the distant delivery months may trade at a lesser price than the near-term delivery months: this is backwardation.
14.1.2 The Put–Call Parity
The price of a put can always be expressed in terms of the price of a call, and conversely. We have the put–call parity:
where ![]() is the common strike price of the call and put,
is the common strike price of the call and put, ![]() is the annualized interest rate,
is the annualized interest rate, ![]() is the expiration time, and
is the expiration time, and ![]() is the time from
is the time from ![]() to
to ![]() in fractions of a year. It is clear that at the expiration we have
in fractions of a year. It is clear that at the expiration we have ![]() . The put–call parity extends this relation for times
. The put–call parity extends this relation for times ![]() before the expiration time
before the expiration time ![]() . Thus, we do not need to know fair values for
. Thus, we do not need to know fair values for ![]() and
and ![]() in order to have an expression for their difference.3
in order to have an expression for their difference.3
14.1.2.1 A Derivation of the Put–Call Parity
Consider portfolio ![]() obtained by buying the call and writing the put:
obtained by buying the call and writing the put:
At the expiration, we have ![]() . Indeed,
. Indeed,

Let ![]() be the forward contract to buy stock at time
be the forward contract to buy stock at time ![]() with price
with price ![]() . This forward contract was valued in (14.1), where we showed that
. This forward contract was valued in (14.1), where we showed that
The replication was obtained by buying the stock and borrowing the amount ![]() . At the expiration, we have
. At the expiration, we have ![]() . Since
. Since ![]() with probability one, we have
with probability one, we have
for all times ![]() before
before ![]() , to exclude arbitrage. This is the statement (14.8) that we wanted to prove.
, to exclude arbitrage. This is the statement (14.8) that we wanted to prove.
14.1.2.2 Bounds for the Call Price
We have bounds for the call price ![]() :
:
The upper bound ![]() is obvious, since the right to buy a stock must be less valuable than the stock itself. To prove the lower bound, we can note that
is obvious, since the right to buy a stock must be less valuable than the stock itself. To prove the lower bound, we can note that ![]() is obvious, since the right to buy a stock involves no obligations.4 The put–call parity and the fact that
is obvious, since the right to buy a stock involves no obligations.4 The put–call parity and the fact that ![]() gives
gives
We have proved the lower bound.5
The lower bound in (14.9) implies that
for ![]() . This follows because
. This follows because ![]() when
when ![]() . The inequality (14.10) leads to the definition of the time value of the option; see (2.6). The lower bound says that the value of the option is larger than the intrinsic value
. The inequality (14.10) leads to the definition of the time value of the option; see (2.6). The lower bound says that the value of the option is larger than the intrinsic value ![]() . The difference of the price of the option and its intrinsic value is called the time value of the European option. For an European put option the lower bound fails unless
. The difference of the price of the option and its intrinsic value is called the time value of the European option. For an European put option the lower bound fails unless ![]() . As a consequence of the put–call parity, the time-value of a put option whose intrinsic value is large (the option is in the money), is usually negative.
. As a consequence of the put–call parity, the time-value of a put option whose intrinsic value is large (the option is in the money), is usually negative.
14.1.3 American Call Options
An American call option has the same price as the corresponding European call option, when the stock does not pay dividends. On the other hand, an American put option has a different price than the corresponding European put option.
The put–call parity was derived for European options. However, this parity can be used to show that
when the stock does not pay dividends, where ![]() is the price of an American call option and
is the price of an American call option and ![]() is the price of the corresponding European call option. We know that
is the price of the corresponding European call option. We know that ![]() , because an American option has more rights than the corresponding European option. The lower bound in (14.9) implies
, because an American option has more rights than the corresponding European option. The lower bound in (14.9) implies
where ![]() is the cash flow generated by the exercise of the American call option. Since
is the cash flow generated by the exercise of the American call option. Since ![]() , an early exercise is always suboptimal and one should sell the American call option and not exercise it. Since it is not optimal to exercise the option, the possibility for the early exercise is not worth of anything, and the American call option has the same value as the European call option.6
, an early exercise is always suboptimal and one should sell the American call option and not exercise it. Since it is not optimal to exercise the option, the possibility for the early exercise is not worth of anything, and the American call option has the same value as the European call option.6
However, an American put option is in general worth more than the corresponding European put option. For the American options we have
The difference between the put and call options comes from the fact that the value of a put option increases as the price of the stock decreases. When the value of the stock decreases, then the absolute price changes become smaller. We can reach the point where the stock takes so small values that further decreases in the stock price would not give a better rate of return to the put option than the risk-free rate. At that point it is better to exercise the option and invest in the risk-free rate. With calls the situation reverses because as the stock price increases, absolute price changes increase. Pricing of American put options in the multiperiod binary model is discussed in Section 14.2.4.
14.2 Pricing in Binary Models
We consider pricing and hedging of derivatives in binary models. In a binary model the stock can at any given time go only one step higher or one step lower. Section 14.2.1 studies one-period binary models. Section 14.2.2 uses one-period binary models as building blocks for multiperiod binary models. A multiperiod binary model approximates the Black–Scholes model, as is shown in Section 14.2.3.
14.2.1 The One-Period Binary Model
First, we describe the one-period binary model. Second, we find the fair price and the optimal hedging coefficient. Third, we find the equivalent martingale measure. Fourth, we provide additional pricing and hedging formulas.
14.2.1.1 A Description of the One-Period Binary Model
In the single period model, there are time points ![]() and
and ![]() . The market consist of stock
. The market consist of stock ![]() , bond
, bond ![]() , and contingent claim
, and contingent claim ![]() .
.
The bond takes value 1 at ![]() and value
and value ![]() at
at ![]() :
:
where ![]() is the risk-free rate.
is the risk-free rate.
The initial value of the stock is ![]() . The stock can take only two values at time 1. At
. The stock can take only two values at time 1. At ![]() the value is
the value is ![]() with probability
with probability ![]() and the value is
and the value is ![]() with probability
with probability ![]() :
:
where ![]() . We assume that
. We assume that
Note that if ![]() , then it would not be rational to invest in the bond, and if
, then it would not be rational to invest in the bond, and if ![]() , then it would not be rational to invest in the stock. The “rationality” can be formalized as the absence of arbitrage.
, then it would not be rational to invest in the stock. The “rationality” can be formalized as the absence of arbitrage.
The contingent claim ![]() takes two possible values
takes two possible values ![]() and
and ![]() at
at ![]() :
:
For example, in the case of a call option we have ![]() for some strike price
for some strike price ![]() . Then
. Then ![]() and
and ![]() .
.
We want to find a fair value ![]() for the derivative at
for the derivative at ![]() . Also, we want to find the optimal hedging coefficient
. Also, we want to find the optimal hedging coefficient ![]() , which is used to hedge the position of the writer of the option.
, which is used to hedge the position of the writer of the option.
14.2.1.2 Pricing and Hedging in the One-Period Binary Model
We replicate the contingent claim ![]() with a portfolio
with a portfolio
The portfolio consists of ![]() units of the bond and
units of the bond and ![]() units of the stock. The portfolio takes values
units of the stock. The portfolio takes values

To obtain ![]() we need to choose
we need to choose ![]() and
and ![]() so that
so that

The first equation leads to
Inserting this value of ![]() to the second equation gives
to the second equation gives
The law of one price implies that the arbitrage-free price ![]() of the contingent claim equals the value
of the contingent claim equals the value ![]() of the replicating portfolio at time
of the replicating portfolio at time ![]() :
: ![]() , and thus
, and thus
where ![]() and
and ![]() are defined in (14.13) and (14.14).
are defined in (14.13) and (14.14).
The number ![]() of bonds can be written as
of bonds can be written as ![]() . Since
. Since ![]() , we can write
, we can write
We can interpret the replicating portfolio from the point of view of the writer of the option as the portfolio where the writer receives the option premium ![]() , invests
, invests ![]() in the bank account, borrows the amount
in the bank account, borrows the amount ![]() from the bank, and invests
from the bank, and invests ![]() in the stock.
in the stock.
14.2.1.3 The Equivalent Martingale Measure
Price ![]() can be written as the expectation with respect to the equivalent martingale measure. We have
can be written as the expectation with respect to the equivalent martingale measure. We have
where

and ![]() means the expectation with respect to the probability measure
means the expectation with respect to the probability measure ![]() with
with
Probability measure ![]() is called a risk-neutral measure because
is called a risk-neutral measure because
and it is called a martingale measure because

Note that condition (14.12) guarantees that ![]() , so that
, so that ![]() is equivalent to
is equivalent to ![]() .
.
14.2.1.4 Further Pricing and Hedging Formulas
It is of interest that the price can be written as
where
Indeed, similarly to (14.13), we get
which can be combined with (14.13) to get
Combining this formula for ![]() with the formula
with the formula ![]() shows (14.19). In (14.19), we have written the derivative price as a discounted expectation of the derivative price, with an additional correction term.
shows (14.19). In (14.19), we have written the derivative price as a discounted expectation of the derivative price, with an additional correction term.
The hedging coefficient can be written as
To derive (14.20), note that

Thus, (14.20) is equal to (14.14). We can also write
where ![]() is the gross return. This way of writing the hedging coefficient appears in (16.10), where quadratic hedging is considered.
is the gross return. This way of writing the hedging coefficient appears in (16.10), where quadratic hedging is considered.
14.2.2 The Multiperiod Binary Model
We start with a description of the multiperiod binary model, and then proceed to the pricing formulas, derive the equivalent martingale measure, and give hedging formulas.
14.2.2.1 A Description of the Multiperiod Binary Model
The market consists of stock ![]() , bond
, bond ![]() , and contingent claim
, and contingent claim ![]() . We define the discrete time processes
. We define the discrete time processes
Note that in Section 13.2 we denoted the time steps of the discrete time markets by ![]() . We have changed the notation, because we construct a time series that approximates the geometric Brownian motion on
. We have changed the notation, because we construct a time series that approximates the geometric Brownian motion on ![]() . The approximation is done by dividing interval
. The approximation is done by dividing interval ![]() to
to ![]() periods of equal lengths and letting
periods of equal lengths and letting ![]() .
.
The bond takes value ![]() at step
at step ![]() , where
, where ![]() is the annualized interest rate, and
is the annualized interest rate, and ![]() is the time between two periods in fractions of a year.
is the time between two periods in fractions of a year.
At step ![]() , the stock can take
, the stock can take ![]() values
values
where
The stock price ![]() is a random variable with
is a random variable with
where ![]() ,
,
The stochastic process of stock prices can be described by a recombining binary tree, as in Figure 14.1, where ![]() . At step
. At step ![]() , the stock takes value
, the stock takes value ![]() (in the figure
(in the figure ![]() ). If the value of the stock at time
). If the value of the stock at time ![]() is
is ![]() , then at step
, then at step ![]() the stock can take values
the stock can take values ![]() and
and ![]() , so that
, so that
The probabilities of the up and down movements are ![]() and
and ![]() :
:

Figure 14.1 A recombining binary tree. There are  periods and the initial value is
periods and the initial value is  .
.
The derivative can take at the expiration ![]() values
values ![]() ,
, ![]() . The random variable
. The random variable ![]() takes the value
takes the value ![]() , when
, when ![]() . For example, when the contingent claim is the call option with
. For example, when the contingent claim is the call option with ![]() , where
, where ![]() is the strike price, then
is the strike price, then ![]() . We have
. We have
We want to find the arbitrage-free price ![]() of the derivative at time
of the derivative at time ![]() .
.
14.2.2.2 Pricing in the Multiperiod Binary Model
The evolution of the stock price in a multiperiod binary model has been described using a recombining binary tree. The price in a multiperiod binary model can be found by backward induction. We know the price at the expiration, when ![]() . We can use the single period model to calculate the price at step
. We can use the single period model to calculate the price at step ![]() , and go backwards step by step to obtain the price at step
, and go backwards step by step to obtain the price at step ![]() . The price
. The price ![]() of the derivative is calculated using the backwards induction with the following steps.
of the derivative is calculated using the backwards induction with the following steps.
- 1. At the expiration step
 , the prices of the derivative are given by
, the prices of the derivative are given by  ,
,  .
. - 2. Let the current step be
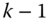 and the current node
and the current node  . Then the two possible prices for the derivative are
. Then the two possible prices for the derivative are  and
and  . We can use the single period model to calculate the price at step
. We can use the single period model to calculate the price at step  . We get the price from (14.17) as
14.26
. We get the price from (14.17) as
14.26
- where

- and the second equality follows from
 and
and  .
.
We have described a recursive algorithm for the computation of the price, but we can also obtain the following explicit expression for the price.
The arbitrage-free price of the derivative is obtained not only at step ![]() , but the price is obtained at all steps
, but the price is obtained at all steps ![]() . In fact, the price of the derivative, under the condition that the stock price at step
. In fact, the price of the derivative, under the condition that the stock price at step ![]() is
is ![]() , is given by the formula
, is given by the formula
14.2.2.3 The Equivalent Martingale Measure
Let us define probability measure ![]() by
by

where ![]() . Measure
. Measure ![]() is obtained from the physical measure
is obtained from the physical measure ![]() , defined in (14.24), by replacing the probability
, defined in (14.24), by replacing the probability ![]() of an up-movement by probability
of an up-movement by probability ![]() . The price in (14.27) can be written as the expectation
. The price in (14.27) can be written as the expectation
where ![]() is the random variable taking value
is the random variable taking value ![]() , when
, when ![]() takes value
takes value ![]() . The measure
. The measure ![]() is called the equivalent martingale measure, or the risk-neutral measure.
is called the equivalent martingale measure, or the risk-neutral measure.
The price ![]() of the derivative given in (14.28), under the condition that the stock price at step
of the derivative given in (14.28), under the condition that the stock price at step ![]() is
is ![]() , can be written as
, can be written as
Accordingly, we can define random variables
Defining

we obtain a more elegant formula
14.2.2.4 Hedging in the Multiperiod Binary Model
The following theorem gives the hedging coefficients of the replicating portfolio. The replication means that the wealth process of the trading strategy obtains the value of the derivative with probability one, or equivalently, the value process of the trading strategy obtains the discounted value of the derivative with probability one. The value process of a self-financing trading strategy is given in (13.8).
There are other ways to write the hedging coefficient. We have from the formula (14.21) of the one-period model that
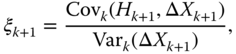
where ![]() ,
, ![]() , and
, and ![]() . Here
. Here ![]() and
and ![]() mean conditional variance and covariance, conditional on
mean conditional variance and covariance, conditional on ![]() , and under probability measure
, and under probability measure ![]() , which is the equivalent martingale measure.
, which is the equivalent martingale measure.
We can also write the hedging coefficient as
Let us prove (14.33). We have from (14.31) that
Thus,

We have shown (14.33).
An additional formula for the hedging coefficient is

In fact, ![]() . Thus,
. Thus,

14.2.3 Asymptotics of the Multiperiod Binary Model
We start with the asymptotic normality of the logarithmic returns in the multiperiod binary model, then show the convergence of the arbitrage-free prices in the multiperiod binary model to the Black–Scholes prices, and finally show the convergence of the hedging coefficients in the multiperiod binary model to the Black–Scholes hedging coefficients.
14.2.3.1 Choice of the Parameters
Let
We consider asymptotics when ![]() . We choose the up and down factors as
. We choose the up and down factors as
where ![]() . We choose the probabilities of the up and down movements as
. We choose the probabilities of the up and down movements as

where ![]() . With these choices the logarithmic return
. With these choices the logarithmic return ![]() converges in distribution to the normal distribution
converges in distribution to the normal distribution ![]() , where
, where ![]() . Note that when we choose
. Note that when we choose ![]() and
and ![]() as in (14.35), then the probability
as in (14.35), then the probability ![]() of the up movement in the risk-neutral distribution is
of the up movement in the risk-neutral distribution is

14.2.3.2 Asymptotic Normality in the Multiperiod Binary Model
We show that the distribution of the stock price in the multiperiod binary model converges in distribution to a log-normal distribution, as the number of steps increases.
In the ![]() -period binary model the stock price
-period binary model the stock price ![]() ,
, ![]() , can be written as
, can be written as

where ![]() are such i.i.d. random variables that
are such i.i.d. random variables that ![]() when
when ![]() is a result of an up-movement and
is a result of an up-movement and ![]() when
when ![]() is a result of a down-movement, so that
is a result of a down-movement, so that

It holds that
as ![]() , where
, where
We show a slightly more general result: For ![]()
as ![]() , where
, where ![]() is such that
is such that ![]() , as
, as ![]() . In particular, we can choose
. In particular, we can choose ![]() . Now (14.38) follows as a special case when we choose
. Now (14.38) follows as a special case when we choose ![]() and
and ![]() .
.
We denote below ![]() . Let us denote
. Let us denote ![]() . We can write
. We can write

where

with ![]() . Now it holds that
. Now it holds that ![]() . We have that
. We have that
- 1.
 ,
, - 2.
 ,
, - 3.
 ,
,
as ![]() . Because
. Because ![]() , the claim (14.39) follows from items 1–3.
, the claim (14.39) follows from items 1–3.
To prove item 1, we note that

Thus,

By the choice of ![]() , it holds
, it holds ![]() as
as ![]() , and thus
, and thus
as ![]() . Thus, item 1 follows by the central limit theorem.
. Thus, item 1 follows by the central limit theorem.
To prove item 2, we use the fact that ![]() , which implies that
, which implies that ![]() as
as ![]() . Thus, the weak law of the large numbers implies item 2.
. Thus, the weak law of the large numbers implies item 2.
To prove item 3, we note that
Item 2 implies that ![]() and since
and since ![]() , we have that
, we have that ![]() , so that
, so that ![]() .
.
14.2.3.3 Convergence of the Price
The arbitrage-free prices (14.27) in the multiperiod binomial model are called the Cox–Ross–Rubinstein prices. We show that the Cox–Ross–Rubinstein put and call prices converge to the Black–Scholes put and call prices, as ![]() . This is done in two steps. First, we show that the put and call prices in the multiperiod binary model converge to the expected values of the option pay-offs, when the expectation is taken with respect to a log-normal distribution. Second, we calculate closed-form expressions for the expected values.
. This is done in two steps. First, we show that the put and call prices in the multiperiod binary model converge to the expected values of the option pay-offs, when the expectation is taken with respect to a log-normal distribution. Second, we calculate closed-form expressions for the expected values.
Bounded Continuous Payoff Functions
A fundamental theorem about weak convergence states that if
- 1.
 ,
, - 2.
 is bounded and continuous,
is bounded and continuous,
then
as ![]() ; see Billingsley (2005, Theorem 25.8, p. 335).
; see Billingsley (2005, Theorem 25.8, p. 335).
- 1. First, we apply the weak convergence in (14.38) to obtain
- where the stock price
 is a random variable taking values
is a random variable taking values  with probabilities
with probabilities

- and
 .
. - 2. Second, we have noted in (14.29) that a Cox–Ross–Rubinstein price satisfies
- where the expectation is with respect to the risk-neutral measure
 , and
, and  is a random variable taking values
is a random variable taking values  , defined by (14.25).
, defined by (14.25).
Let ![]() be such function that
be such function that ![]() Then the option payoff can be written as
Then the option payoff can be written as
If function ![]() is continuous and bounded, then (14.40) and (14.41) imply that
is continuous and bounded, then (14.40) and (14.41) imply that
where the distribution of ![]() is defined by
is defined by
and we used the fact that ![]() , because
, because ![]() .
.
Unbounded Continuous Payoff Functions
The fundamental theorem about weak convergence applies for any sequence converging weakly. However, in our case we are interested in the special case of the convergence of a binomial distribution toward a log-normal distribution. In this special case Föllmer and Schied (2002, Proposition 5.39, p. 265) notes that the convergence of expectations can be proved also when we relax the condition of the boundedness. Let ![]() be measurable, almost everywhere continuous, and
be measurable, almost everywhere continuous, and
Then,
Put Prices
The payoff function of a put option is
where ![]() is the strike price. Function
is the strike price. Function ![]() ,
, ![]() , is bounded and continuous. Thus, the Cox–Ross–Rubinstein price
, is bounded and continuous. Thus, the Cox–Ross–Rubinstein price ![]() of an European put option converges to the expectation:
of an European put option converges to the expectation:
The right hand side is equal to the Black–Scholes put price, as shown in (14.54).
Call Prices
The payoff function of a call option is
where ![]() is the strike price. Function
is the strike price. Function ![]() ,
, ![]() , is continuous but not bounded. Thus, the convergence of the Cox–Ross–Rubinstein price to the expected value cannot be inferred similarly as in the case of put options. However, we can apply the put-call parity in (14.8) to conclude that the Cox–Ross–Rubinstein prices have to satisfy
, is continuous but not bounded. Thus, the convergence of the Cox–Ross–Rubinstein price to the expected value cannot be inferred similarly as in the case of put options. However, we can apply the put-call parity in (14.8) to conclude that the Cox–Ross–Rubinstein prices have to satisfy
where ![]() is the Cox–Ross–Rubinstein call price, and
is the Cox–Ross–Rubinstein call price, and ![]() the put price. Since we have shown (14.45), it holds that
the put price. Since we have shown (14.45), it holds that
The right hand side is equal to the Black–Scholes call price, as shown in (14.52).
Calculation of the Expectations
We have proved in (14.45) and (14.46) that the arbitrage-free put and call prices in the multiperiod binary model approach the expected values of the option payoffs, when the expectations are with respect to the equivalent martingale measure (the risk neutral log-normal model). Thus, we want to calculate the expected values of the put and call payoffs. The expected values are the Black–Scholes prices, which we denote
and
where the expectations are taken with respect to the distribution of ![]() defined by
defined by
where ![]() and
and
Note that we have discussed the log-normal distribution in (3.50).
The density of the standard normal distribution is ![]() , where
, where ![]() . Then,
. Then,

where

By writing ![]() we have
we have
Thus,
where ![]() is the distribution function of the standard normal distribution. Since
is the distribution function of the standard normal distribution. Since ![]() ,
,
where

because ![]() and
and ![]() . This leads to the call price
. This leads to the call price
Similarly,
which leads to the put price
We have calculated explicit expressions for the call and put prices at time ![]() , when the stock price is
, when the stock price is ![]() . The Black–Scholes call and put prices at time
. The Black–Scholes call and put prices at time ![]() , when the stock price is
, when the stock price is ![]() , are given by
, are given by
and
where the expectations are taken with respect to the distribution of ![]() defined by
defined by
where ![]() and
and ![]() . The corresponding explicit expressions are given in (14.58) and (14.59), and the Black–Scholes prices are discussed in Section 14.3.1.
. The corresponding explicit expressions are given in (14.58) and (14.59), and the Black–Scholes prices are discussed in Section 14.3.1.
14.2.3.4 Convergence of the Hedging Coefficient
We show that the hedging coefficients of puts and calls in the multiperiod binary model converge to the Black–Scholes hedging coefficients. The Black–Scholes hedging coefficients are called deltas, and they are obtained by differentiating the Black–Scholes prices with respect to the stock price.
Let the initial time and the initial stock price be
Let ![]() be either the Black–Scholes call price or the put price at time
be either the Black–Scholes call price or the put price at time ![]() , when the stock price at time
, when the stock price at time ![]() is
is ![]() , and the expiration is at time
, and the expiration is at time ![]() . These prices are written as expectations in (14.55) and (14.56), and in a more explicit form in (14.58) and (14.59).
. These prices are written as expectations in (14.55) and (14.56), and in a more explicit form in (14.58) and (14.59).
Let us consider step ![]() of the multiperiod binary model. Let
of the multiperiod binary model. Let ![]() be one of the possible stock prices at step
be one of the possible stock prices at step ![]() , where
, where ![]() . These prices were defined in (14.23). Let
. These prices were defined in (14.23). Let ![]() be such that
be such that
as ![]() . In particular, we can choose
. In particular, we can choose ![]() , where
, where ![]() is the largest integer
is the largest integer ![]() . Choose
. Choose

Then
as ![]() .
.
The hedging coefficient of the multiperiod binary model was written in (14.32) as

where ![]() and
and ![]() are the two possible prices of the derivative at step
are the two possible prices of the derivative at step ![]() , when the value of the stock at step
, when the value of the stock at step ![]() is
is ![]() .7 Now it holds that
.7 Now it holds that
where ![]() is the derivative of the Black–Scholes price with respect to stock price.
is the derivative of the Black–Scholes price with respect to stock price.
To show (14.57), note that from (14.46) and (14.45), and the continuity of the functions ![]() we have that
we have that
where ![]() means that
means that ![]() . Thus,
. Thus,

Also, ![]() ,
, ![]() , and
, and ![]() , as
, as ![]() .
.
14.2.3.5 Rate of Convergence
Figure 14.2 illustrates the convergence of (a) the ratio of the Cox–Ross–Rubinstein call price to the Black–Scholes call price, and (b) the ratio of the Cox–Ross–Rubinstein call hedging coefficient to the Black–Scholes call hedging coefficient. The ratios are plotted as a function of the number ![]() of the steps in the multiperiod binary model, where
of the steps in the multiperiod binary model, where ![]() . The moneyness
. The moneyness ![]() is 0.9 (green), 0.95 (black), and 1 (red). The annualized volatility is
is 0.9 (green), 0.95 (black), and 1 (red). The annualized volatility is ![]() , the interest rate is
, the interest rate is ![]() , and the time to maturity is 1 month:
, and the time to maturity is 1 month: ![]() . We see that the convergence of the at-the-money options is faster than the convergence of the out-of-the-money options.
. We see that the convergence of the at-the-money options is faster than the convergence of the out-of-the-money options.

Figure 14.2 Convergence of the Cox–Ross–Rubinstein price and hedging coefficient. Plotted are (a) the ratios of the Cox–Ross–Rubinstein call price to the Black–Scholes price and (b) the ratios of the Cox–Ross–Rubinstein call hedging coefficient to the Black–Scholes hedging coefficient as a function of  . The three curves show the cases where the moneyness is
. The three curves show the cases where the moneyness is  (green),
(green),  (black), and
(black), and  (red).
(red).
14.2.3.6 Asian and Knock-Out-Options
We have proved the weak convergence at one point: Let ![]() and
and ![]() . Then
. Then
where ![]() is the price of the stock at step
is the price of the stock at step ![]() in the multiperiod binomial model, and
in the multiperiod binomial model, and ![]() is the price of the stock at time
is the price of the stock at time ![]() in the geometric Brownian motion model. If the option payoff is
in the geometric Brownian motion model. If the option payoff is ![]() , then the price in the multiperiod binomial model converges to the price of the option whose payoff is
, then the price in the multiperiod binomial model converges to the price of the option whose payoff is ![]() in the geometric Brownian motion model. Asian options and knock-out options depend on values of stocks in more than one point.
in the geometric Brownian motion model. Asian options and knock-out options depend on values of stocks in more than one point.
Asian Options
In the case of Asian options, the option payoffs can be written as
where ![]() are steps, and
are steps, and ![]() are fixed time points. For example, in the case of an Asian call option
are fixed time points. For example, in the case of an Asian call option

The corresponding prices converge for a suitable ![]() , when
, when
Knock-Out Options
The payoffs of knock-out options depend on the trajectory of the prices through
Let us divide the time interval ![]() into
into ![]() subintervals. Denote the
subintervals. Denote the ![]() boundaries of the intervals by
boundaries of the intervals by
Points ![]() fill the interval
fill the interval ![]() asymptotically. We can define a continuous time process
asymptotically. We can define a continuous time process ![]() ,
, ![]() , by linearly interpolating
, by linearly interpolating ![]() : define
: define

when ![]() . Geometric Brownian motion
. Geometric Brownian motion ![]() is defined in (5.62). We can show that process
is defined in (5.62). We can show that process ![]() converges weakly to the geometric Brownian motion
converges weakly to the geometric Brownian motion
where ![]() is the standard Brownian motion. The weak convergence
is the standard Brownian motion. The weak convergence
as ![]() , happens in the metric space
, happens in the metric space ![]() of the continuous functions on
of the continuous functions on ![]() . The prices of the options whose payoffs are
. The prices of the options whose payoffs are
converge for suitable ![]() .
.
14.2.4 American Put Options
An American put option has a different price than the corresponding European put option, and the price of an American put option does not have a closed-form expression in the multiperiod binary model. However, an American call option has the same price as the corresponding European call option, when the stock does not pay dividends (see Section 14.1.3). Thus, the American call options can be priced similarly as the European call options using the Black–Scholes prices or the recombining binary trees.
The American put options have to be priced by taking into account the possibility of an early exercise. We can use the recombining binary tree to price the American put options. At every node of the tree we consider whether it is better to exercise or to keep the option for a future exercise. We are not able to obtain a closed-form formula for the price of the American put options, but we obtain an algorithm for the computation of the price. First, the single period binary model is studied. Second, the multiperiod binary model leads to the final algorithm.
14.2.4.1 American Put Options in the One-Period Binary Model
In the one-period binary model, the American put option can be exercised at time ![]() or at time
or at time ![]() . Let us denote with
. Let us denote with ![]() the value of the American put option at time
the value of the American put option at time ![]() and let us denote with
and let us denote with ![]() the value of the European put option at time
the value of the European put option at time ![]() . An arbitrage argument shows that
. An arbitrage argument shows that
The value of an European put option can be obtained from (14.17) as
where
with

14.2.4.2 American Put Options in the Multiperiod Binary Model
The price of an American put option is determined in the ![]() -step binomial model by recursion. Remember that in the
-step binomial model by recursion. Remember that in the ![]() -step binomial model the possible prices at step
-step binomial model the possible prices at step ![]() ,
, ![]() , are
, are
with
The recursive steps are the following.
- 1. At time
 the prices of the American put option are given by
the prices of the American put option are given by

 .
. - 2. At time
 ,
,  , when the stock has price
, when the stock has price  , we know from the previous steps of the algorithm that the two possible prices for the derivative at time
, we know from the previous steps of the algorithm that the two possible prices for the derivative at time  are
are  and
and  . We can use the single period model to calculate the price at time
. We can use the single period model to calculate the price at time  . We get the price from the one-step binary model as
. We get the price from the one-step binary model as

- where

- and

- with
 .
.
14.3 Black–Scholes Pricing
First we describe the properties of Black–Scholes call and put prices, second we discuss implied volatility, third we describe various ways to derive the Black–Scholes prices, and fourth we give Black–Scholes formulas for options on forwards, for fixed income options, and for currency options.
14.3.1 Call and Put Prices
The Black–Scholes price of the call option at time ![]() , with strike price
, with strike price ![]() , and with the maturity date
, and with the maturity date ![]() , is equal to
, is equal to
where ![]() is the stock price at time
is the stock price at time ![]() ,
, ![]() is the annualized risk-free rate,
is the annualized risk-free rate,

and ![]() is the distribution function of the standard Gaussian distribution. The time
is the distribution function of the standard Gaussian distribution. The time ![]() to expiration is expressed in fractions of a year. The put price is equal to
to expiration is expressed in fractions of a year. The put price is equal to
Note that it can be convenient to write

The Black–Scholes price is derived under the assumption of a log-normal distribution of the stock price: It is assumed that at time ![]()
where ![]() ,
, ![]() is the drift, and
is the drift, and ![]() is the volatility. Note that under the risk-neutral measure
is the volatility. Note that under the risk-neutral measure ![]() . The volatility
. The volatility ![]() is the only unknown parameter that need to be estimated, since
is the only unknown parameter that need to be estimated, since ![]() does not appear in the price formula.
does not appear in the price formula.
14.3.1.1 Computation of Black–Scholes Prices
For the application of the Black–Scholes formula the time ![]() is taken as the time in fractions of year. For example, when the time to expiration is 20 trading days, then
is taken as the time in fractions of year. For example, when the time to expiration is 20 trading days, then ![]() . Alternatively, when time to expiration is 20 calendar days, then
. Alternatively, when time to expiration is 20 calendar days, then ![]() .
.
The risk-free rate ![]() is expressed as the annualized rate.
is expressed as the annualized rate.
The only unknown parameter ![]() has to be estimated. Let
has to be estimated. Let ![]() be an equally spaced sample of stock prices and let us denote
be an equally spaced sample of stock prices and let us denote ![]() for
for ![]() . We assume that
. We assume that ![]()
![]() , are i.i.d.
, are i.i.d. ![]() , so that the stock prices satisfy (3.50). We can estimate
, so that the stock prices satisfy (3.50). We can estimate ![]() with the sample variance
with the sample variance

where ![]() . Then an estimator of
. Then an estimator of ![]() is
is
For example, if we sample stock prices daily, then ![]() and
and ![]() .8 If we sample stock prices monthly, then
.8 If we sample stock prices monthly, then ![]() and
and ![]() The normalized sample standard deviation in (14.60) is called the annualized sample standard deviation.
The normalized sample standard deviation in (14.60) is called the annualized sample standard deviation.
14.3.1.2 Characteristics of Black–Scholes Prices
We study the qualitative behavior of the Black–Scholes prices as a function of five parameters ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
The prices of calls and puts increase as ![]() increases. We have
increases. We have
and
which are the bounds derived from the put–call parity in (14.9). The prices of calls and puts increase as the time to maturity ![]() increases. The price of a call increases as
increases. The price of a call increases as ![]() increases and the price of a call decreases as
increases and the price of a call decreases as ![]() increases, but for puts the relations reverse. The price of a call increases as the interest rate
increases, but for puts the relations reverse. The price of a call increases as the interest rate ![]() increases but the price of a put decreases as the interest rate
increases but the price of a put decreases as the interest rate ![]() increases.
increases.
Figure 14.3 shows Black–Scholes prices for calls and puts as a function of the call moneyness ![]() . The call prices increase and the put prices decrease as a function of moneyness. Panel (a) shows the cases of annualized volatility
. The call prices increase and the put prices decrease as a function of moneyness. Panel (a) shows the cases of annualized volatility ![]() (black),
(black), ![]() (red), and
(red), and ![]() (green). The time to maturity is 20 trading days and the interest rate is
(green). The time to maturity is 20 trading days and the interest rate is ![]() . Panel (b) shows the cases of interest rates
. Panel (b) shows the cases of interest rates ![]() (black),
(black), ![]() (red), and
(red), and ![]() (green). The time to maturity is 20 trading days and the annualized volatility is
(green). The time to maturity is 20 trading days and the annualized volatility is ![]() . We see from panel (a) that increasing volatility increases the prices, both for call and puts. The effect of increasing time to maturity is similar. We see from panel (b) that for calls increasing interest rates increases prices, but for puts increasing interest rates decreases prices.
. We see from panel (a) that increasing volatility increases the prices, both for call and puts. The effect of increasing time to maturity is similar. We see from panel (b) that for calls increasing interest rates increases prices, but for puts increasing interest rates decreases prices.

Figure 14.3 Call and put prices as a function of call moneyness  . The call prices increase and the put prices decrease as a function of moneyness. (a) The annualized volatility is
. The call prices increase and the put prices decrease as a function of moneyness. (a) The annualized volatility is  (black),
(black),  (red), and
(red), and  (green); (b) the interest rate is
(green); (b) the interest rate is  (black),
(black),  (red), and
(red), and  (green).
(green).
Figure 14.4 shows that the call and put prices are not symmetric. The ratios of call prices to put prices are shown as a function of the call moneyness ![]() : We show the functions
: We show the functions

where ![]() is the current stock price. The strike prices for the calls take values
is the current stock price. The strike prices for the calls take values ![]() , and the corresponding strike prices for the puts are
, and the corresponding strike prices for the puts are ![]() . Panel (a) shows the cases of annualized volatility
. Panel (a) shows the cases of annualized volatility ![]() (black),
(black), ![]() (red), and
(red), and ![]() (green). The interest rate is
(green). The interest rate is ![]() . Panel (b) shows the cases of interest rates
. Panel (b) shows the cases of interest rates ![]() (black),
(black), ![]() (red), and
(red), and ![]() (green). The annualized volatility is
(green). The annualized volatility is ![]() . The time to maturity is 20 trading days in both panels. We see that the call prices are higher than the put prices for out-of-the-money options. This is related to the asymmetry of the log-normal distribution (see Figure 3.11). For at-the-money options the difference between the call and the put prices is not large. Increasing the volatility makes the ratios of the call and put prices closer to one, and decreasing the interest rate makes the ratios of the call and put prices closer to one.
. The time to maturity is 20 trading days in both panels. We see that the call prices are higher than the put prices for out-of-the-money options. This is related to the asymmetry of the log-normal distribution (see Figure 3.11). For at-the-money options the difference between the call and the put prices is not large. Increasing the volatility makes the ratios of the call and put prices closer to one, and decreasing the interest rate makes the ratios of the call and put prices closer to one.

Figure 14.4 Ratios of call prices to put prices as a function of moneyness  . (a) Annualized volatility is
. (a) Annualized volatility is  (black),
(black),  (red), and
(red), and  (green); (b) interest rate is
(green); (b) interest rate is  (black),
(black),  (red), and
(red), and  (green).
(green).
14.3.1.3 Black–Scholes Prices and Volatility
To apply Black–Scholes prices we need to estimate the volatility. We study how the Black–Scholes prices change when the volatility estimate changes. We apply the data of S&P 500 daily prices, described in Section 2.4.1.
Figure 14.5 shows time series of Black–Scholes call prices. The volatility is equal to the sequential annualized sample standard deviation. Panel (a) shows call prices with moneyness ![]() and panel (b) shows call prices with moneyness
and panel (b) shows call prices with moneyness ![]() . The time to expiration is either 20 trading days (black curves) or 30 trading days (red curves). The risk-free rates are deduced from 1-month Treasury bill rates. We can see that the time series of Black–Scholes prices follow closely to the time series of sequential standard deviations in Figure 7.5.
. The time to expiration is either 20 trading days (black curves) or 30 trading days (red curves). The risk-free rates are deduced from 1-month Treasury bill rates. We can see that the time series of Black–Scholes prices follow closely to the time series of sequential standard deviations in Figure 7.5.

Figure 14.5 Time series of Black–Scholes call prices. (a) Moneyness  and (b) moneyness
and (b) moneyness  . Call prices are computed using the sequential sample standard deviation. The time to expiration is 20 trading days (black) or 30 trading days (red).
. Call prices are computed using the sequential sample standard deviation. The time to expiration is 20 trading days (black) or 30 trading days (red).
Figure 14.6 studies Black–Scholes prices when the volatility is equal to the sequentially estimated GARCH(![]() ) volatility. Panel (a) shows time series of call prices with moneyness
) volatility. Panel (a) shows time series of call prices with moneyness ![]() (black) and
(black) and ![]() (green). The time to expiration is 20 trading days. Panel (b) shows kernel density estimates of the distributions of the prices. The horizontal and the vertical lines show the Black–Scholes prices when the volatility is the annualized sample standard deviation computed from the complete sample. The risk-free rate is zero.
(green). The time to expiration is 20 trading days. Panel (b) shows kernel density estimates of the distributions of the prices. The horizontal and the vertical lines show the Black–Scholes prices when the volatility is the annualized sample standard deviation computed from the complete sample. The risk-free rate is zero.

Figure 14.6 Black–Scholes prices with GARCH-volatility. (a) Time series of prices; (b) kernel estimates of the density of the collection of prices. The moneyness is  (black) and
(black) and  (green).
(green).
14.3.1.4 The Greeks
The greeks are defined by differentiating the option price with respect to the price of the underlying, the time to the expiration, the interest rate, or the volatility. In this section, we denote the Black–Scholes call and put prices by
where ![]() is the current time,
is the current time, ![]() is the current price of the underlying,
is the current price of the underlying, ![]() is the strike price,
is the strike price, ![]() is the time of the expiration,
is the time of the expiration, ![]() is the volatility, and
is the volatility, and ![]() is the interest rate. Sometimes we leave out some of the arguments and denote, for example,
is the interest rate. Sometimes we leave out some of the arguments and denote, for example, ![]() .
.
The Delta
The delta is the derivative of the price function with respect to the underlying. The delta is the hedging coefficient in the Black–Scholes hedging, as discussed in Section 14.4. The call and put delta are
We have that
In fact, if ![]() increases, then the price of the call increases and the price of the put decreases:
increases, then the price of the call increases and the price of the put decreases: ![]() and
and ![]() . The absolute value of the change in the value of a call or a put cannot exceed the absolute value of the change in the underlying:
. The absolute value of the change in the value of a call or a put cannot exceed the absolute value of the change in the underlying: ![]() and
and ![]() .
.
The call delta is equal to
and the put delta equal to
Let us calculate the call delta. The delta of a call is given in (14.62) because

and finally9
Figure 14.7 shows the call delta as a function of moneyness ![]() . In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate
. In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate ![]() and the dashed lines show the case of interest rates
and the dashed lines show the case of interest rates ![]() . The more interesting part is the moneyness
. The more interesting part is the moneyness ![]() . In this region the deltas are
. In this region the deltas are ![]() in both panels. Panel (a) shows that when moneyness is
in both panels. Panel (a) shows that when moneyness is ![]() , then a larger volatility leads to a larger delta. Panel (b) shows that increasing time to maturity has a similar qualitative effect as increasing volatility.
, then a larger volatility leads to a larger delta. Panel (b) shows that increasing time to maturity has a similar qualitative effect as increasing volatility.

Figure 14.7 Call deltas. Call deltas are shown as a function of moneyness  . (a) The annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is
. (a) The annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is  (solid lines) and
(solid lines) and  (dashed lines).
(dashed lines).
Figure 14.8 shows a time series of Black–Scholes deltas using the data of S&P 500 daily prices, described in Section 2.4.1. The daily prices are used to create a time series with the sampling frequency of 20 and 30 trading days. Panel (a) shows call prices with moneyness ![]() and panel (b) shows call prices when moneyness
and panel (b) shows call prices when moneyness ![]() . The time to expiration is either 20 trading days (black curves) or 30 trading days (red curves). The volatility is equal to the sequential sample standard deviation. The risk-free rates are deduced from 1-month Treasury bill rates. The corresponding time series of Black–Scholes prices is given in Figure 14.5.
. The time to expiration is either 20 trading days (black curves) or 30 trading days (red curves). The volatility is equal to the sequential sample standard deviation. The risk-free rates are deduced from 1-month Treasury bill rates. The corresponding time series of Black–Scholes prices is given in Figure 14.5.

Figure 14.8 Time series of Black–Scholes call deltas. (a) Moneyness  and (b) moneyness
and (b) moneyness  . Call deltas are computed using the sequential sample standard deviation. The time to expiration is 20 trading days (black) or 30 trading days (red).
. Call deltas are computed using the sequential sample standard deviation. The time to expiration is 20 trading days (black) or 30 trading days (red).
The Gamma
The gamma is the second derivative of the price function with respect to the underlying:

The price functions are convex with respect to ![]() and thus
and thus
The call gamma and the put gamma are given by

Figure 14.9 shows the call gamma as a function of moneyness ![]() . In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate
. In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate ![]() and the dashed lines show the case of interest rates
and the dashed lines show the case of interest rates ![]() .
.

Figure 14.9 Call gammas. Call gammas are shown as a function of moneyness  . (a) The annualized volatility is 10% (black) and 20% (red) with the time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is
. (a) The annualized volatility is 10% (black) and 20% (red) with the time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is  (solid lines) and
(solid lines) and  (dashed lines).
(dashed lines).
Theta
The theta is the derivative of the price function with respect to time:
As ![]() increases the value of the option decreases (everything else being equal) and thus
increases the value of the option decreases (everything else being equal) and thus
The call theta is equal to

and the put theta is equal to

Figure 14.10 shows the call theta as a function of moneyness ![]() . In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate
. In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate ![]() and the dashed lines show the case of interest rates
and the dashed lines show the case of interest rates ![]() .
.

Figure 14.10 Call thetas. Call thetas are shown as a function of moneyness 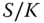 . (a) The annualized volatility is 10% (black) and 20% (red) with the time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is
. (a) The annualized volatility is 10% (black) and 20% (red) with the time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is  (solid lines) and
(solid lines) and  (dashed lines).
(dashed lines).
Vega
The vega is the derivative of the price function with respect to volatility:
The call vega and the put vega are equal to
Figure 14.11 shows the call vega as a function of moneyness ![]() . In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate
. In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate ![]() and the dashed lines show the case of interest rates
and the dashed lines show the case of interest rates ![]() .
.

Figure 14.11 Call vega. Call vegas are shown as a function of moneyness  . (a) The annualized volatility is 10% (black) and 20% (red) with the time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is
. (a) The annualized volatility is 10% (black) and 20% (red) with the time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is  (solid lines) and
(solid lines) and  (dashed lines).
(dashed lines).
Rho
The rho is the derivative of the price function with respect to interest rate:
The call rho is equal to
and the put rho is equal to
Figure 14.12 shows the call rho as a function of moneyness ![]() . In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate
. In panel (a) the annualized volatility is 10% (black) and 20% (red) with time to expiration 1 month. In panel (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The solid lines show the case of interest rate ![]() and the dashed lines show the case of interest rates
and the dashed lines show the case of interest rates ![]() .
.

Figure 14.12 Call rho. Call rhos are shown as a function of moneyness  . (a) The annualized volatility is 10% (black) and 20% (red) with the time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is
. (a) The annualized volatility is 10% (black) and 20% (red) with the time to expiration 1 month; (b) the time to expiration is 1 month (black) and 3 months (red) with volatility 10%. The interest rate is  (solid lines) and
(solid lines) and  (dashed lines).
(dashed lines).
14.3.2 Implied Volatilities
Implied volatilities can be derived both from call prices or from put prices. Let ![]() be a Black–Scholes call price. The mapping
be a Black–Scholes call price. The mapping
is bijective and can be inverted. Let us denote by ![]() the inverse of mapping (14.64). When we observe a market price
the inverse of mapping (14.64). When we observe a market price ![]() for a call option, then
for a call option, then
is the implied volatility of the option. The implied volatility of a put option can be defined similarly.
14.3.2.1 Quoting Option Prices
It is helpful to quote option prices using implied volatilities. Option prices and implied volatilities are in a bijective correspondence, but it is easier to compare the prices of options with different maturities and strike prices using the implied volatilities than using the market prices. This is analogous to expressing the bond prices with annualized rates instead of quoted prices.10 The implied volatilities can be used to quote prices even when we do not think that the Black–Scholes prices are fair prices, similarly as the bond rates can be defined using various conventions.
14.3.2.2 The Volatility Surface
If the Black–Scholes model describes the true distribution of the asset prices, and if the market prices coincide with the Black–Scholes prices, then the implied volatilities of options with different strike prices and with different maturities are all equal. However, in practice the implied volatilities are different for the options with different strike prices and with different maturities.
The volatility surface gives for each strike price and for each maturity the corresponding implied volatility. Let ![]() be the market prices of call (put) options with strike prices
be the market prices of call (put) options with strike prices ![]() and expiration dates
and expiration dates ![]() , where
, where ![]() ,
, ![]() . The options are otherwise similar. The volatility surface is the function
. The options are otherwise similar. The volatility surface is the function
where ![]() is the time to the expiration.
is the time to the expiration.
The volatility surface is typically not a constant function. Instead, for a fixed maturity ![]() , function
, function
is typically u-shaped (smile) or skew (one sided smile). Instead of the strike ![]() one may take as the argument the moneyness
one may take as the argument the moneyness ![]() (or
(or ![]() ), or the delta of the options.
), or the delta of the options.
Options written on equity indices yield often skews. This might be due to the fact that a crash in stock markets leads to increased volatility, whereas a rise in stock markets is not usually involved with an increased volatility. Options on various interest rates yield more monotonous one sided smiles than the equity indices.
Currency markets yield often symmetric smiles. Currency markets are more symmetric than stock markets because a big movement in either direction results in an increased volatility (it is always a crash for one of the currencies).
The smile tends to flatten out with maturity. This might be due to the better Gaussian approximation when the maturity is longer.
14.3.2.3 Pricing of Options Using Implied Volatilities
Out-of-the-money options can be priced in the following way. (1) Find the implied volatility of at-the-money options. (2) Adjust the implied volatility (using experience) to get a new volatility. (3) Calculate the price of the out-of-the-money option using the new volatility.
14.3.2.4 VIX Index
The VIX index of CBOE (Chicago Board Options Exchange) uses prices of options to derive the volatility that is expected by the markets. Section 6.3.1 contains a discussion of the VIX index and Figure 6.5 shows a time series of the VIX index. Let us derive the formula of the VIX index.
It is assumed that the stock price follows a geometric Brownian motion, as defined in (5.62). That is,
where ![]() is the standard Brownian motion,
is the standard Brownian motion, ![]() , and
, and ![]() . Under the equivalent martingale measure
. Under the equivalent martingale measure ![]() , where
, where ![]() is the yearly risk-free interest rate. Thus, for the equivalent martingale measure we have
is the yearly risk-free interest rate. Thus, for the equivalent martingale measure we have

We can solve for ![]() to get
to get

A Taylor expansion gives

where ![]() . Thus,
. Thus,

Theorem 13.2 implies that when the expectation is taken with respect to a risk-neutral measure, then
where ![]() and
and ![]() are the arbitrage-free prices of the call and the put. Under the risk-neutral measure
are the arbitrage-free prices of the call and the put. Under the risk-neutral measure

where ![]() is the futures price, as given in (14.2). Thus,
is the futures price, as given in (14.2). Thus,

We arrive at the variance formula
The variance formula (14.65) was derived in Demeterfi et al. (1999). CBOE uses the approximation

CBOE:s VIX index is defined as11

where ![]() is the midpoint of the bid-ask spread for the option, and
is the midpoint of the bid-ask spread for the option, and ![]() . The calculation is done for two expiration dates, and the final index value is a weighted average of these. Note that the put–call parity (14.8) gives the equality
. The calculation is done for two expiration dates, and the final index value is a weighted average of these. Note that the put–call parity (14.8) gives the equality ![]() .
.
14.3.3 Derivations of the Black–Scholes Prices
We have derived the Black–Scholes prices as the limits of the prices in the multiperiod binary model. Now we describe shortly the martingale derivation of the Black–Scholes prices, derivation of the prices using the Black–Scholes differential equation, and the derivation of the prices using the put–call parity.
14.3.3.1 Martingale Derivation
The second fundamental theorem of asset pricing says that an arbitrage-free market model is complete if and only if there exists exactly one equivalent martingale measure. We have stated this theorem for the discrete time model in Theorem 13.3.
The Black–Scholes prices can be derived as a corollary of the second fundamental theorem of asset pricing: If the Black–Scholes market model is arbitrage-free and complete, then the Black–Scholes prices are the discounted expectations with respect to the equivalent martingale measure.
Shiryaev (1999, p. 710) states in a continuous time framework that if there exists a unique equivalent martingale measure, then the unique arbitrage-free price of the option is the discounted expected value of the payoff with respect to the unique equivalent martingale measure.
We give a sketch of some elements of the derivation of the Black–Scholes prices directly from the second fundamental theorem of asset pricing. Details can be found in Shiryaev (1999, p. 739).
The Black–Scholes model assumes that the stock price follows the geometric Brownian motion, as defined in (5.62). The stock price satisfies
and the bank account satisfies
where ![]() .12 Thus,
.12 Thus,
The Girsanov's theorem was stated in (5.64). We apply Girsanov's theorem with the constant function ![]() . Then,
. Then,
is a Brownian motion with respect to measure ![]() , defined by
, defined by ![]() , where
, where

Measure ![]() is the unique martingale measure that is equivalent to
is the unique martingale measure that is equivalent to ![]() ; see Shiryaev (1999, p. 708). Thus, the price of the call option
; see Shiryaev (1999, p. 708). Thus, the price of the call option ![]() is
is
We need to find the distribution of ![]() under
under ![]() . From (14.68) we obtain that
. From (14.68) we obtain that

Thus,

14.3.3.2 The Black–Scholes Differential Equation
Black and Scholes (1973) and Merton (1973) derived the Black–Scholes price by solving a differential equation. The Black–Scholes partial differential equation is
where ![]() is the value of the option at time
is the value of the option at time ![]() ,
, ![]() is the theta of the option,
is the theta of the option, ![]() is the delta of the option,
is the delta of the option, ![]() is the gamma of the option, and
is the gamma of the option, and ![]() . When
. When ![]() is the value of a call option, then the solution is found under the boundary condition
is the value of a call option, then the solution is found under the boundary condition
The price of the option is ![]() . The differential equation is solved, for example, in Shiryaev (1999, p. 746).
. The differential equation is solved, for example, in Shiryaev (1999, p. 746).
The Black–Scholes partial differential equation can be derived heuristically in the following way. Itô's lemma (5.61) applied to the function ![]() gives
gives
Assume that value ![]() of the option is replicated by the portfolio
of the option is replicated by the portfolio
that is,
The assumptions ![]() and
and ![]() imply
imply
Equating (14.70) and (14.71) gives ![]() , that is,
, that is,

This means that we want a perfect replication of ![]() . Choose
. Choose ![]() , which is called delta hedging. This makes
, which is called delta hedging. This makes ![]() to disappear and leads to the differential equation (14.69). Delta hedging has removed all uncertainty, and we have obtained a perfect hedge.
to disappear and leads to the differential equation (14.69). Delta hedging has removed all uncertainty, and we have obtained a perfect hedge.
14.3.3.3 Derivation of the Prices Using the Put–Call parity
We can derive the Black–Scholes prices for the calls and puts using the put–call parity given in Section 14.1.2. The basic idea is that if we are willing to assume that the prices are expectations with respect to a log-normal distribution, then the put–call parity implies that the log-normal distribution should be the risk-neutral log-normal distribution.
We assume that the distribution of the stock price ![]() is defined by (14.49). Let us denote by
is defined by (14.49). Let us denote by ![]() the price of the call option at time
the price of the call option at time ![]() . We assume that the price of the call option is equal to
. We assume that the price of the call option is equal to
and the value of the put option is equal to
Thus, using (14.50) and (14.53),
because ![]() for all
for all ![]() . The put–call parity (14.8) implies that we have to take
. The put–call parity (14.8) implies that we have to take
Inserting (14.72) to (14.50) and (14.53) leads to (14.58) and (14.59). This derivation was noted in Derman and Taleb (2005).
14.3.4 Examples of Pricing Using the Black–Scholes Model
We give some examples of Black–Scholes prices. The examples include pricing functions of options on a forward, caplets, swaptions, options on a foreign currency, and barrier options.
14.3.4.1 Options on a Forward
Let the underlying be a futures contract ![]() with the maturity
with the maturity ![]() . Consider a call option with the expiration time
. Consider a call option with the expiration time ![]() . The payoff is
. The payoff is ![]() , where
, where ![]() is the strike price. The price of the call option is obtained by replacing
is the strike price. The price of the call option is obtained by replacing ![]() in the Black–Scholes formula (14.58) by
in the Black–Scholes formula (14.58) by ![]() . This gives the price
. This gives the price
where

The volatility ![]() is the volatility of the stock. This is called Black's formula, and it was introduced in Black (1976).
is the volatility of the stock. This is called Black's formula, and it was introduced in Black (1976).
Why have we replaced ![]() with
with ![]() ? This is due to the fact that under the risk-neutral measure the stock price has the distribution
? This is due to the fact that under the risk-neutral measure the stock price has the distribution
The pricing formula of the futures contract in (14.2) gives ![]() . Thus, the distribution of
. Thus, the distribution of ![]() under the risk-neutral measure is
under the risk-neutral measure is
The distribution of ![]() is
is
where ![]() . The price of the call option is
. The price of the call option is
and this expectation is calculated similarly as in (14.51).
The formula (14.73) holds when the option is subject to the stock type settlement. If the option is subject to the futures type settlement, then set ![]() in (14.73). The futures type settlement means that the gains and losses are realized daily, whereas in the stock type settlement the gain or loss is realized at the time of liquidation.
in (14.73). The futures type settlement means that the gains and losses are realized daily, whereas in the stock type settlement the gain or loss is realized at the time of liquidation.
14.3.4.2 Caplets
Caplets are discussed in Section 18.3.1. A caplet is a call option on the Libor rate ![]() . The payoff of a caplet at time
. The payoff of a caplet at time ![]() is
is
where ![]() is the principal, and
is the principal, and ![]() is the strike. We assume that under the risk-neutral measure
is the strike. We assume that under the risk-neutral measure
where ![]() and
and ![]() is the forward rate, defined in (18.14). Note that at time
is the forward rate, defined in (18.14). Note that at time ![]() the forward Libor rate is equal to the spot Libor rate:
the forward Libor rate is equal to the spot Libor rate: ![]() . The Black's formula for the price of the caplet is
. The Black's formula for the price of the caplet is

where

The caplet price can be written as the expectation
where the expectation is with respect to the risk-neutral distribution in (14.74). The expectation is calculated similarly as in (14.51). The caplet price ![]() is obtained from the Black–Scholes price of a call option on a stock when
is obtained from the Black–Scholes price of a call option on a stock when ![]() is replaced by
is replaced by ![]() and
and ![]() is replaced by
is replaced by ![]() .
.
Caps are defined in Section 18.3.2. Let ![]() be the time points for the caplets on the Libor rates
be the time points for the caplets on the Libor rates ![]() , where
, where ![]() . A cap is priced by
. A cap is priced by

where ![]() are the prices of the caplets.
are the prices of the caplets.
14.3.4.3 Swaptions
Swaptions are discussed in Section 18.3.3. Let ![]() be the current time,
be the current time, ![]() be the expiry time, and
be the expiry time, and ![]() be the maturity time of the swaption. The payoff of an European call option on a swap is given in (18.27) as
be the maturity time of the swaption. The payoff of an European call option on a swap is given in (18.27) as
where ![]() is the equilibrium swap rate,
is the equilibrium swap rate, ![]() is the strike,
is the strike,

![]() is the principal, and
is the principal, and ![]() is a zero-coupon bond. We assume that under the risk-neutral measure
is a zero-coupon bond. We assume that under the risk-neutral measure
where ![]() . The Black's formula for the price of the swaption is
. The Black's formula for the price of the swaption is
where

The swaption price can be written as the expectation
where the expectation is with respect to the risk-neutral distribution in (14.74). The expectation is calculated similarly as in (14.51). The caplet price ![]() is obtained from the Black–Scholes price of a call option on a stock when
is obtained from the Black–Scholes price of a call option on a stock when ![]() is replaced by
is replaced by ![]() and
and ![]() is replaced by
is replaced by ![]() .
.
Note that the simultaneous log-normality for all caplets and all swaptions is not consistent because a swap rate is a linear combination of forward rates and cannot be log-normal if the underlying forward rates are.
14.3.4.4 Options on a Foreign Currency
Let ![]() be the price of a foreign currency in the domestic currency units. The payoff of an European call option on a foreign currency is given by
be the price of a foreign currency in the domestic currency units. The payoff of an European call option on a foreign currency is given by
where ![]() is the strike, and
is the strike, and ![]() is the expiration time. According the Garman–Kohlhagen model, under the risk-neutral measure,
is the expiration time. According the Garman–Kohlhagen model, under the risk-neutral measure,
where ![]() . Then the price of the call option is
. Then the price of the call option is
where

where ![]() is the risk-free rate in the foreign currency and
is the risk-free rate in the foreign currency and ![]() is the risk-free rate in the domestic currency. The put price is
is the risk-free rate in the domestic currency. The put price is
The price of the call option can be written as
where the expectation is with respect to the risk-neutral measure. The expectation is calculated similarly as in (14.51).
The call price ![]() on the exchange rate is obtained from the Black–Scholes price of a call option on a stock when
on the exchange rate is obtained from the Black–Scholes price of a call option on a stock when ![]() is replaced by the exchange rate
is replaced by the exchange rate ![]() and
and ![]() is replaced by
is replaced by ![]() .
.
14.3.4.5 Down-and-Out Call
A down-and-out call on stock ![]() has the payoff
has the payoff

where ![]() is the strike price and
is the strike price and ![]() is the barrier. We assume that the stock price has a log-normal distribution
is the barrier. We assume that the stock price has a log-normal distribution
under the risk-neutral measure, where ![]() . The price of the down-and-out call is
. The price of the down-and-out call is
where ![]() is the Black–Scholes price of the vanilla call and
is the Black–Scholes price of the vanilla call and

where

14.4 Black–Scholes Hedging
The hedging coefficients of calls and puts are given in (14.61). The Black–Scholes hedging coefficients are equal to the deltas of options. A delta is the derivative of the price of the option with respect to the price of the underlying: the call and put deltas are
This is shown in Section 14.2.3; see (14.57).13 For the Black–Scholes pricing functions the call delta and the put delta are shown in (14.62) and (14.63) to be equal to
and
In this section, our purpose is to illustrate how hedging can be used to approximately replicate options, and to study how hedging frequency, expected stock returns, and the volatility of stock returns affect the replication. The study is made using Black–Scholes hedging, since Black–Scholes hedging provides a benchmark for comparing various hedging methods.
We take the purpose of hedging to be to make the probability distribution of the hedging error of the writer of the option as concentrated around zero as possible. We consider S&P 500 options and estimate the distribution of the hedging error of the writer using the S&P 500 daily data of Section 2.4.1.
Section 14.4.1 reviews historical simulation for the estimation of the distribution of the hedging error. Section 14.4.2 studies the effect of hedging frequency to the distribution of the terminal wealth. Section 14.4.3 studies the effect of the strike price, Section 14.4.4 studies the effect of the mean return, and Section 14.4.5 studies the effect of the return volatility.
14.4.1 Hedging Errors: Nonsequential Volatility Estimation
We have discussed the estimation of the hedging error using historical simulation in Section 13.3.1. Let us write the formulas for hedging error again, this time taking into account the varying hedging frequencies.
14.4.1.1 Hedging Errors
The hedging error ![]() of the writer of the option is obtained from (13.10) by the formula
of the writer of the option is obtained from (13.10) by the formula
where

when we take the risk-free rate ![]() . Here
. Here ![]() is the price of the option,
is the price of the option, ![]() is the terminal value of the option,
is the terminal value of the option, ![]() are the hedging coefficients, and
are the hedging coefficients, and ![]() are the stock prices. In (14.78) the current time is denoted by
are the stock prices. In (14.78) the current time is denoted by ![]() , the time to expiration is
, the time to expiration is ![]() days, and hedging is done daily. The hedging can be done with a lesser frequency. When hedging is done
days, and hedging is done daily. The hedging can be done with a lesser frequency. When hedging is done ![]() times during the period
times during the period ![]() , then
, then

where
14.4.1.2 Historical Simulation
Let us denote the time series of observed historical daily prices by ![]() . Let us denote the time to the expiration by
. Let us denote the time to the expiration by
(The interpretation is that the last observation ![]() is made at time
is made at time ![]() , and we are interested to write an option whose expiration time is
, and we are interested to write an option whose expiration time is ![]() .) We construct
.) We construct ![]() sequences of prices:
sequences of prices:
where
for ![]() . Each sequence has length
. Each sequence has length ![]() and the initial prices are always
and the initial prices are always ![]() . We estimate the distribution of the hedging error
. We estimate the distribution of the hedging error ![]() from the observations
from the observations
where ![]() is computed from the prices
is computed from the prices ![]() . For the estimation of the density we use both the histogram estimator and the kernel density estimator, defined in Section 3.2.2.
. For the estimation of the density we use both the histogram estimator and the kernel density estimator, defined in Section 3.2.2.
We consider hedging of call options. The Black–Scholes prices are given in (14.58) and the hedging coefficients are given in (14.62). The volatility ![]() is estimated using the annualized sample standard deviation, computed from the complete data. We study the effect of volatility estimation to hedging in Section 14.5, where sequential (out-of-sample) volatility estimation is studied. In this section, we use in-sample volatility estimation.
is estimated using the annualized sample standard deviation, computed from the complete data. We study the effect of volatility estimation to hedging in Section 14.5, where sequential (out-of-sample) volatility estimation is studied. In this section, we use in-sample volatility estimation.
More precisely, the ![]() th hedging error is
th hedging error is

where ![]() is the Black–Scholes price from (14.58), computed with the stock price
is the Black–Scholes price from (14.58), computed with the stock price ![]() , time to expiration
, time to expiration ![]() , and volatility
, and volatility ![]() . Here
. Here ![]() is the annualized sample standard deviation computed from return data
is the annualized sample standard deviation computed from return data
where

![]() . Thus, the volatility is estimated in-sample. The hedging coefficient
. Thus, the volatility is estimated in-sample. The hedging coefficient ![]() is the Black–Scholes delta from (14.62), computed with the stock price
is the Black–Scholes delta from (14.62), computed with the stock price ![]() , time to expiration
, time to expiration ![]() , and volatility
, and volatility ![]() . The terminal value is
. The terminal value is ![]() .
.
14.4.2 Hedging Frequency
In this section, we illustrate how a change in the hedging frequency changes the distribution of the hedging error. We study hedging of S&P 500 call options, using daily data of Section 2.4.1. The time to expiration is 20 days. The volatility in the Black–Scholes formula is the non-sequential annualized sample standard deviation.
14.4.2.1 Moneyness 
Figure 14.13 shows time series of hedging errors. Panel (a) shows the case when there is no hedging, so that ![]() . Panel (b) shows the case when the hedging is done daily. Moneyness is
. Panel (b) shows the case when the hedging is done daily. Moneyness is ![]() .
.

Figure 14.13 Hedging frequency: Time series of hedging errors. (a) There is no hedging; (b) hedging is done daily.
Figure 14.14 shows tails plots of the hedging errors. Panel (a) shows the left tail plots and panel (b) shows the right tail plots. We show cases of no hedging (red), hedging once (black), hedging twice (blue), and hedging 20 times (green).

Figure 14.14 Hedging frequency: Tail plots. (a) Left tail plots and (b) right tail plots. We show cases of no hedging (red), hedging once (black), hedging twice (blue), and hedging 20 times (green).
Figure 14.15 shows (a) histograms of hedging errors and (b) kernel density estimates of the distribution of hedging errors. Panel (a) shows cases of no hedging (red) and daily hedging (green). Panel (b) shows additionally the cases of hedging once (black) and hedging twice (blue). Note that the red kernel density estimate is very inaccurate, because the underlying distribution is such that a large part of the probability mass is concentrated at one point.

Figure 14.15 Hedging frequency: Density estimates of hedging errors. (a) Histograms; (b) kernel density estimates. Panel (a) shows cases of no hedging (red) and hedging 20 times (green). Panel (b) shows additionally the cases of hedging once (black) and hedging twice (blue).
14.4.2.2 Moneyness 
Figure 14.16 shows tails plots of the hedging errors. Panel (a) shows the left tail plots and panel (b) shows the right tail plots. We show cases of no hedging (red), hedging once (black), hedging twice (blue), and hedging 20 times (green).

Figure 14.16 Hedging frequency: Tail plots with moneyness  . (a) Left tail plots; (b) right tail plots. We show cases of no hedging (red), hedging once (black), hedging twice (blue), and hedging 20 times (green).
. (a) Left tail plots; (b) right tail plots. We show cases of no hedging (red), hedging once (black), hedging twice (blue), and hedging 20 times (green).
Figure 14.17 shows (a) histograms of hedging errors and (b) kernel density estimates of the distribution of hedging errors when the moneyness is ![]() . Panel (a) shows cases of no hedging (red) and daily hedging (green). Panel (b) shows additionally the cases of hedging once (black) and hedging twice (blue). The red kernel density estimate is very inaccurate, because the underlying distribution is such that a large part of the probability mass is concentrated at one point.
. Panel (a) shows cases of no hedging (red) and daily hedging (green). Panel (b) shows additionally the cases of hedging once (black) and hedging twice (blue). The red kernel density estimate is very inaccurate, because the underlying distribution is such that a large part of the probability mass is concentrated at one point.

Figure 14.17 Hedging frequency: Density estimates of hedging errors with moneyness  . (a) Histograms; (b) kernel density estimates. Panel (a) shows cases of no hedging (red) and hedging 20 times (green). Panel (b) shows additionally the cases of hedging once (black) and hedging twice (blue).
. (a) Histograms; (b) kernel density estimates. Panel (a) shows cases of no hedging (red) and hedging 20 times (green). Panel (b) shows additionally the cases of hedging once (black) and hedging twice (blue).
14.4.2.3 Expected Utility
Figure 14.18 shows the estimated expected utility as a function of the hedging frequency. In panel (a) the moneyness is ![]() . In panel (b)
. In panel (b) ![]() . We apply the exponential utility function
. We apply the exponential utility function ![]() , where the risk-aversion parameter takes values
, where the risk-aversion parameter takes values ![]() (black),
(black), ![]() (red), and
(red), and ![]() (blue). The expected utilities are estimated using the sample averages. Increasing hedging frequency clearly increases the expected utility. We can see that when the risk aversion is small, then the increase in the expected utility as a function of hedging frequency is much smaller than the increase when the risk aversion is large.
(blue). The expected utilities are estimated using the sample averages. Increasing hedging frequency clearly increases the expected utility. We can see that when the risk aversion is small, then the increase in the expected utility as a function of hedging frequency is much smaller than the increase when the risk aversion is large.

Figure 14.18 Expected utility as a function of hedging frequency. (a) The moneyness is  ; (b)
; (b)  . The risk aversion parameter takes values
. The risk aversion parameter takes values 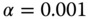 (black),
(black),  (red), and
(red), and  (blue).
(blue).
14.4.3 Hedging and Strike Price
In this section, we illustrate how a change in the strike price changes the distribution of the hedging error. We study hedging of S&P 500 call options, using daily data of Section 2.4.1. The time to expiration is 20 days and hedging is done daily. The volatility in the Black–Scholes formula is the nonsequential annualized sample standard deviation.
Figure 14.19(a) shows tail plots of hedging errors and panel (b) shows kernel density estimates of the distribution of the hedging error. The strikes prices of calls are ![]() (red),
(red), ![]() (black), and
(black), and ![]() (blue), when the stock price is
(blue), when the stock price is ![]() . For in-the-money options the distributions have a larger spread than for out-of-the-money options. Also, the distributions for at-the-money options have a center that is located to the right from the centers for out-of-the-money options.
. For in-the-money options the distributions have a larger spread than for out-of-the-money options. Also, the distributions for at-the-money options have a center that is located to the right from the centers for out-of-the-money options.

Figure 14.19 Several strike prices. (a) Tail plots; (b) kernel density estimates. The strike prices are  (red),
(red),  (black), and
(black), and  (blue), when the stock price is
(blue), when the stock price is  .
.
14.4.4 Hedging and Expected Return
We study the effect of the mean return to the distribution of the hedging error. This is done by manipulating the S&P 500 data. We change observations so that the new net returns are
where ![]() are the observed net returns,
are the observed net returns, ![]() is the sample mean of
is the sample mean of ![]() , and
, and ![]() is a value for the expected return that we choose. The new prices are obtained from the net returns by
is a value for the expected return that we choose. The new prices are obtained from the net returns by

For the S&P 500 returns the annualized mean return is about ![]() . We try the annualized expected returns
. We try the annualized expected returns ![]() and
and ![]() . Thus,
. Thus, ![]() and
and ![]() .
.
Figure 14.20 shows histogram estimates of the distribution of the hedging error when the expected annualized return is ![]() . In panel (a) there is no hedging and in panel (b) there is daily hedging. That is, panel (a) shows a histogram made from realizations of the random variable
. In panel (a) there is no hedging and in panel (b) there is daily hedging. That is, panel (a) shows a histogram made from realizations of the random variable ![]() , where
, where ![]() , and
, and ![]() is the Black–Scholes price. Panel (b) shows a histogram made from realizations of the random variable
is the Black–Scholes price. Panel (b) shows a histogram made from realizations of the random variable ![]() . The time to the expiration of the call option is
. The time to the expiration of the call option is ![]() days, and the strike price is
days, and the strike price is ![]() with the initial stock price
with the initial stock price ![]() . Since
. Since ![]() is large the call option gives a profit to its owner with a large probability, as can be seen from panel (a). However, large
is large the call option gives a profit to its owner with a large probability, as can be seen from panel (a). However, large ![]() does not change much the distribution of the hedging error when hedging is done daily, as can be seen from panel (b). In fact, the corresponding distribution of the hedging error when the expected return is moderate is shown in Figure 14.15.
does not change much the distribution of the hedging error when hedging is done daily, as can be seen from panel (b). In fact, the corresponding distribution of the hedging error when the expected return is moderate is shown in Figure 14.15.

Figure 14.20 No hedging versus daily hedging with a large positive drift. (a) No hedging: A histogram from realizations of  . (b) Daily hedging: A histogram from realizations of
. (b) Daily hedging: A histogram from realizations of  .
.
Figure 14.21 shows the setting of Figure 14.20 when the annualized expected return is ![]() , instead of
, instead of ![]() . Panel (a) shows the distribution of the hedging error of the writer when no hedging is done and panel (b) shows the hedging error when delta hedging is done daily. Since the expected return is negative, the writer of the call option gets a profit with a large probability, but this does not affect much the hedging error when the hedging is done daily, as can be seen from panel (b).
. Panel (a) shows the distribution of the hedging error of the writer when no hedging is done and panel (b) shows the hedging error when delta hedging is done daily. Since the expected return is negative, the writer of the call option gets a profit with a large probability, but this does not affect much the hedging error when the hedging is done daily, as can be seen from panel (b).

Figure 14.21 No hedging versus daily hedging with a negative drift. (a) No hedging: A histogram from realizations of  . (b) Daily hedging: A histogram from realizations of
. (b) Daily hedging: A histogram from realizations of  .
.
(1) When the drift is larger than the risk-free rate, then the Black–Scholes price ![]() is smaller than the expectation
is smaller than the expectation ![]() . The possibility of hedging makes
. The possibility of hedging makes ![]() smaller than
smaller than ![]() . The expectation
. The expectation ![]() increases when the drift increases but the possibility of hedging makes the price independent of the drift. (2) When the drift is equal to the risk-free rate, then
increases when the drift increases but the possibility of hedging makes the price independent of the drift. (2) When the drift is equal to the risk-free rate, then ![]() is close to
is close to ![]() , but hedging reduces the risk of the writer of the option, because it changes the wealth distribution of the writer of the option. (3) When the drift is negative, then
, but hedging reduces the risk of the writer of the option, because it changes the wealth distribution of the writer of the option. (3) When the drift is negative, then ![]() is smaller than
is smaller than ![]() , and hedging reduces the expected profit of the writer of the option. However, the hedging reduces also the risk of the writer of the option, and thus hedging is reasonable even in the case of negative drift.
, and hedging reduces the expected profit of the writer of the option. However, the hedging reduces also the risk of the writer of the option, and thus hedging is reasonable even in the case of negative drift.
14.4.5 Hedging and Volatility
We study the effect of the return volatility to the distribution of the hedging error. We manipulate the S&P 500 data by changing observations so that the new net returns are
where ![]() are the observed net returns,
are the observed net returns, ![]() is the sample standard deviation of
is the sample standard deviation of ![]() ,
, ![]() is the sample mean of
is the sample mean of ![]() , and
, and ![]() is a value of our choice for the volatility. The new prices are obtained from the net returns by
is a value of our choice for the volatility. The new prices are obtained from the net returns by
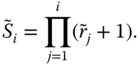
For the S&P 500 returns the annualized sample standard deviation is about ![]() . We try the annualized standard deviation
. We try the annualized standard deviation ![]() . Thus,
. Thus, ![]() .
.
Figure 14.22 shows histogram estimates of the distribution of the hedging error when the annualized volatility is ![]() . In panel (a) there is no hedging, and in panel (b) there is daily hedging. That is, panel (a) shows a histogram made from realizations of the random variable
. In panel (a) there is no hedging, and in panel (b) there is daily hedging. That is, panel (a) shows a histogram made from realizations of the random variable ![]() , where
, where ![]() , and
, and ![]() is the Black–Scholes price. Panel (b) shows a histogram made from realizations of the random variable
is the Black–Scholes price. Panel (b) shows a histogram made from realizations of the random variable ![]() . The time to the expiration is
. The time to the expiration is ![]() days, and the strike price is
days, and the strike price is ![]() with the initial stock price
with the initial stock price ![]() . We see that the larger volatility makes the dispersion of the probability distribution of the hedging error larger.
. We see that the larger volatility makes the dispersion of the probability distribution of the hedging error larger.

Figure 14.22 Large volatility. (a) No hedging: A histogram of realizations of  . (b) Daily hedging: A histogram of realizations of
. (b) Daily hedging: A histogram of realizations of  .
.
14.5 Black–Scholes Hedging and Volatility Estimation
We continue to study the distribution of the hedging error ![]() , as in Section 14.4. In this section, our aim is to study how the volatility estimation affects the distribution of the hedging error. The Black–Scholes prices and the hedging coefficients depend on the annualized volatility
, as in Section 14.4. In this section, our aim is to study how the volatility estimation affects the distribution of the hedging error. The Black–Scholes prices and the hedging coefficients depend on the annualized volatility ![]() . We compare the performance of GARCH(
. We compare the performance of GARCH(![]() ) and exponentially weighted moving averages for the estimation of
) and exponentially weighted moving averages for the estimation of ![]() . The performance of Black–Scholes hedging will be used as a benchmark.
. The performance of Black–Scholes hedging will be used as a benchmark.
14.5.1 Hedging Errors: Sequential Volatility Estimation
We have discussed in Section 13.3.1 the estimation of the distribution of the hedging error using historical simulation. We write again the formulas for the hedging error and historical simulation, adapting to the current setting.
14.5.1.1 Hedging Errors
The hedging error ![]() of the writer of the option is obtained from (13.10) as
of the writer of the option is obtained from (13.10) as
where

Here the risk-free rate is ![]() ,
, ![]() is the price of the option,
is the price of the option, ![]() is the terminal value of the option,
is the terminal value of the option, ![]() are the hedging coefficients,
are the hedging coefficients, ![]() are the stock prices, the current time is denoted by 0, the time to expiration is
are the stock prices, the current time is denoted by 0, the time to expiration is ![]() days, and hedging is done daily.
days, and hedging is done daily.
14.5.1.2 Historical Simulation
We denote the time series of observed historical daily prices by ![]() . We construct
. We construct ![]() sequences of prices:
sequences of prices:
where
for ![]() . Each sequence has length
. Each sequence has length ![]() and the initial price in each sequence is
and the initial price in each sequence is ![]() . We estimate the distribution of the hedging error
. We estimate the distribution of the hedging error ![]() from the observations
from the observations
where ![]() is computed from the prices
is computed from the prices ![]() .
.
More precisely, the ![]() th hedging error is
th hedging error is
where ![]() is the Black–Scholes price from (14.58), computed with the stock price
is the Black–Scholes price from (14.58), computed with the stock price ![]() , time to expiration
, time to expiration ![]() , and volatility
, and volatility ![]() . Here
. Here ![]() is the annualized volatility estimate computed using return data
is the annualized volatility estimate computed using return data
where

Thus, the volatility estimation is done sequentially (out-of-sample). The hedging coefficient ![]() is the Black–Scholes delta from (14.62), computed with the stock price
is the Black–Scholes delta from (14.62), computed with the stock price ![]() , time to expiration
, time to expiration ![]() , and volatility
, and volatility ![]() . The terminal value is
. The terminal value is ![]() .
.
For the estimation of the density we use both the histogram estimator and the kernel density estimator, defined in Section 3.2.2.
14.5.2 Distribution of Hedging Errors
In the following examples the time to expiration is ![]() trading days. We start pricing and hedging after 4 years of data has been collected. The risk-free rate is equal to zero. We consider S&P 500 call options and use the daily S&P 500 data, described in Section 2.4.1.
trading days. We start pricing and hedging after 4 years of data has been collected. The risk-free rate is equal to zero. We consider S&P 500 call options and use the daily S&P 500 data, described in Section 2.4.1.
As a summary of the results, we can note that the GARCH(![]() ) and the exponential moving average (with a suitable smoothing parameter) improve the distribution of the hedging error from the point of view of the writer of the option, when compared to the sequential sample standard deviation. GARCH(
) and the exponential moving average (with a suitable smoothing parameter) improve the distribution of the hedging error from the point of view of the writer of the option, when compared to the sequential sample standard deviation. GARCH(![]() ) and the exponential moving average lead to a distribution whose left tail is lighter: with these volatility estimators the losses of the writer of the option are smaller. On the other hand, GARCH(
) and the exponential moving average lead to a distribution whose left tail is lighter: with these volatility estimators the losses of the writer of the option are smaller. On the other hand, GARCH(![]() ) and the exponential moving average lead to larger positive hedging errors. The positive hedging errors are gains for the writer of the option.
) and the exponential moving average lead to larger positive hedging errors. The positive hedging errors are gains for the writer of the option.
Figure 14.23 shows (a) the means of negative hedging errors and (b) the means of positive hedging errors as a function of the moneyness ![]() . The arithmetic means of positive and negative hedging errors are defined as
. The arithmetic means of positive and negative hedging errors are defined as
where the hedging errors ![]() are defined in (14.81). The hedging is done with sequentially computed sample standard deviation (red with “s”), GARCH(
are defined in (14.81). The hedging is done with sequentially computed sample standard deviation (red with “s”), GARCH(![]() ) volatility (blue with “g”), the exponential moving average with
) volatility (blue with “g”), the exponential moving average with ![]() (yellow with “1”), and with smoothing parameter
(yellow with “1”), and with smoothing parameter ![]() (green with “2”). We see that the sample standard deviation is the best for the positive hedging errors and the worst for the negative hedging errors. The performance of GARCH(
(green with “2”). We see that the sample standard deviation is the best for the positive hedging errors and the worst for the negative hedging errors. The performance of GARCH(![]() ) and the exponentially weighted moving average with
) and the exponentially weighted moving average with ![]() are close to each other. The exponentially weighted moving average with
are close to each other. The exponentially weighted moving average with ![]() has the performance between the sample standard deviation and the GARCH(
has the performance between the sample standard deviation and the GARCH(![]() ). We can see that hedging errors are larger for the at-the-money options than for the out-of-the-money options.
). We can see that hedging errors are larger for the at-the-money options than for the out-of-the-money options.

Figure 14.23 Means of hedging errors. The figure shows the means of (a) negative hedging errors as a function of moneyness and (b) positive hedging errors. The volatility is estimated by the sequentially computed sample standard deviation (red with “s”), GARCH(1,1) (blue with “g”), the exponential moving average with  (yellow with “1”), and with
(yellow with “1”), and with  (green with “2”).
(green with “2”).

Figure 14.24 Distribution of hedging errors. The figure shows (a) tail plots of hedging errors and (b) kernel density estimates of the distribution of the hedging error. The volatility is estimated by the sequentially computed sample standard deviation (red), GARCH( ) (blue), and the exponential moving average with
) (blue), and the exponential moving average with  (green).
(green).

Figure 14.25 Distribution of hedging errors: Moving averages. The figure shows (a) tail plots of hedging errors and (b) kernel density estimates of the distribution of the hedging error. The volatility is estimated by the sequentially computed standard deviation (red), and by the exponentially weighted moving average with  (purple),
(purple),  (green),
(green),  (blue), and
(blue), and  (black).
(black).
Figure 14.24 shows (a) tail plots of hedging errors and (b) kernel density estimates of the distribution of the hedging error. The moneyness of call options is ![]() . The volatility is estimated by the sequentially computed standard deviation (red), by GARCH(
. The volatility is estimated by the sequentially computed standard deviation (red), by GARCH(![]() ) (blue), and by the exponentially weighted moving average with
) (blue), and by the exponentially weighted moving average with ![]() (green). Tail plots are defined in Section 3.2.1 and the kernel density estimator is defined in Section 3.2.2. We apply the standard normal kernel function and the smoothing parameter is chosen by the normal reference rule.
(green). Tail plots are defined in Section 3.2.1 and the kernel density estimator is defined in Section 3.2.2. We apply the standard normal kernel function and the smoothing parameter is chosen by the normal reference rule.
Figure 14.25 shows (a) tail plots of hedging errors and (b) kernel density estimates of the hedging error. The volatility is estimated by the sequentially computed standard deviation (red), and by the exponentially weighted moving average with ![]() (purple),
(purple), ![]() (green),
(green), ![]() (blue), and
(blue), and ![]() (black).
(black).

since ![]() for the risk-neutral measure
for the risk-neutral measure ![]() .
.


where ![]() is the number of stocks that are bought at time
is the number of stocks that are bought at time ![]() to hedge the position until
to hedge the position until ![]() . The amount
. The amount ![]() is borrowed with the risk-free rate at time
is borrowed with the risk-free rate at time ![]() . If the hedging gives a position without risk, we should have
. If the hedging gives a position without risk, we should have ![]() , which gives
, which gives

when ![]() . This gives the instantaneous optimal hedging coefficient as
. This gives the instantaneous optimal hedging coefficient as