When a meteorologist provides a weather forecast, precipitation is typically predicted using terms such as "70 percent chance of rain." These forecasts are known as probability of precipitation reports. Have you ever considered how they are calculated? It is a puzzling question, because in reality, it will either rain or it will not.
These estimates are based on probabilistic methods, or methods concerned with describing uncertainty. They use data on past events to extrapolate future events. In the case of weather, the chance of rain describes the proportion of prior days with similar measurable atmospheric conditions in which precipitation occurred. A 70 percent chance of rain therefore implies that in 7 out of 10 past cases with similar weather patterns, precipitation occurred somewhere in the area.
This chapter covers a machine learning algorithm called naive Bayes, which also uses principles of probability for classification. Just as meteorologists forecast weather, naive Bayes uses data about prior events to estimate the probability of future events. For instance, a common application of naive Bayes uses the frequency of words in past junk email messages to identify new junk mail. While studying how this works, you will learn:
- Basic principles of probability that are utilized for naive Bayes
- Specialized methods, visualizations, and data structures used for analyzing text data with R
- How to employ an R implementation of naive Bayes classifier to build an SMS message filter
If you've taken a statistics class before, some of the material in this chapter may seem like a bit of a review of the subject. Even so, it may be helpful to refresh your knowledge of probability, as these principles are the basis of how naive Bayes got such a strange name.
The basic statistical ideas necessary to understand the naive Bayes algorithm have been around for centuries. The technique descended from the work of the 18th century mathematician Thomas Bayes, who developed foundational mathematical principles (now known as Bayesian methods) for describing the probability of events, and how probabilities should be revised in light of additional information.
We'll go more in depth later, but for now it suffices to say that the probability of an event is a number between 0 percent and 100 percent that captures the chance that the event will occur given the available evidence. The lower the probability, the less likely the event is to occur. A probability of 0 percent indicates that the event definitely will not occur, while a probability of 100 percent indicates that the event certainly will occur.
Classifiers based on Bayesian methods utilize training data to calculate an observed probability of each class based on feature values. When the classifier is used later on unlabeled data, it uses the observed probabilities to predict the most likely class for the new features. It's a simple idea, but it results in a method that often has results on par with more sophisticated algorithms. In fact, Bayesian classifiers have been used for:
- Text classification, such as junk email (spam) filtering, author identification, or topic categorization
- Intrusion detection or anomaly detection in computer networks
- Diagnosing medical conditions, when given a set of observed symptoms
Typically, Bayesian classifiers are best applied to problems in which the information from numerous attributes should be considered simultaneously in order to estimate the probability of an outcome. While many algorithms ignore features that have weak effects, Bayesian methods utilize all available evidence to subtly change the predictions. If a large number of features have relatively minor effects, taken together their combined impact could be quite large.
Before jumping into the naive Bayes algorithm, it's worth spending some time defining the concepts that are used across Bayesian methods. Summarized in a single sentence, Bayesian probability theory is rooted in the idea that the estimated likelihood of an event should be based on the evidence at hand. Events are possible outcomes, such as sunny and rainy weather, a heads or tails result in a coin flip, or spam and not spam email messages. A trial is a single opportunity for the event to occur, such as a day's weather, a coin flip, or an email message.
The probability of an event can be estimated from observed data by dividing the number of trials in which an event occurred by the total number of trials. For instance, if it rained 3 out of 10 days, the probability of rain can be estimated as 30 percent. Similarly, if 10 out of 50 email messages are spam, then the probability of spam can be estimated as 20 percent. The notation P(A) is used to denote the probability of event A, as in P(spam) = 0.20.
The total probability of all possible outcomes of a trial must always be 100 percent. Thus, if the trial only has two outcomes that cannot occur simultaneously, such as heads or tails, or spam and ham (non-spam), then knowing the probability of either outcome reveals the probability of the other. For example, given the value P(spam) = 0.20, we are able to calculate P(ham) = 1 – 0.20 = 0.80. This works because the events spam and ham are mutually exclusive and exhaustive. This means that the events cannot occur at the same time and are the only two possible outcomes. As shorthand, the notation P(¬A) can be used to denote the probability of event A not occurring, as in P(¬spam) = 0.80.
For illustrative purposes, it is often helpful to imagine probability as a two-dimensional space that is partitioned into event probabilities for events. In the following diagram, the rectangle represents the set of all possible outcomes for an email message. The circle represents the probability that the message is spam. The remaining 80 percent represents the messages that are not spam:

Often, we are interested in monitoring several non-mutually exclusive events for the same trial. If some events occur with the event of interest, we may be able to use them to make predictions. Consider, for instance, a second event based on the outcome that the email message contains the word Viagra. For most people, this word is only likely to appear in a spam message; its presence in a message is therefore a very strong piece of evidence that the email is spam. The preceding diagram, updated for this second event, might appear as shown in the following diagram:

Notice in the diagram that the Viagra circle does not completely fill the spam circle, nor is it completely contained by the spam circle. This implies that not all spam messages contain the word Viagra, and not every email with the word Viagra is spam.
To zoom in for a closer look at the overlap between the spam and Viagra circles, we'll employ a visualization known as a Venn diagram. First used in the late 19th century by John Venn, the diagram uses circles to illustrate the overlap between sets of items. In most Venn diagrams such as the following one, the size of the circles and the degree of the overlap is not important. Instead, it is used as a way to remind you to allocate probability to all possible combinations of events.

We know that 20 percent of all messages were spam (the left circle), and 5 percent of all messages contained spam (the right circle). Our job is to quantify the degree of overlap between these two proportions. In other words, we hope to estimate the probability of both P(spam) and P(Viagra) occurring, which can be written as P(spam ∩ Viagra).
Calculating P(spam ∩ Viagra) depends on the joint probability of the two events, or how the probability of one event is related to the probability of the other. If the two events are totally unrelated, they are called independent events. For instance, the outcome of a coin flip is independent from whether the weather is rainy or sunny.
If all events were independent, it would be impossible to predict any event using the data obtained by another. On the other hand, dependent events are the basis of predictive modeling. For instance, the presence of clouds is likely to be predictive of a rainy day, and the appearance of the word Viagra is predictive of a spam email.
With the knowledge that P(spam) and P(Viagra) were independent, we could then easily calculate P(spam ∩ Viagra); the probability of both events happening at the same time. Because 20 percent of all messages are spam, and 5 percent of all emails contain the word Viagra, we could assume that 5 percent of 20 percent (0.05 * 0.20 = 0.01), or 1 percent of all messages are spam containing the word Viagra. More generally, for independent events A and B, the probability of both happening is P(A ∩ B) = P(A) * P(B).
In reality, it is far more likely that P(spam) and P(Viagra) are highly dependent, which means that this calculation is incorrect. We need to use a more careful formulation of the relationship between these two events.
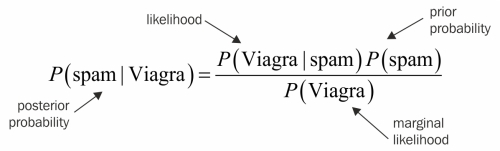
The relationships between dependent events can be described using Bayes' theorem, as shown in the following formula. The notation P(A|B) can be read as the probability of event A given that event B occurred. This is known as conditional probability, since the probability of A is dependent (that is, conditional) on what happened with event B.

To understand how Bayes' theorem works in practice, suppose that you were tasked with guessing the probability that an incoming email was spam. Without any additional evidence, the most reasonable guess would be the probability that any prior message was spam (that is, 20 percent in the preceding example). This estimate is known as the prior probability.
Now, also suppose that you obtained an additional piece of evidence; you were told that the incoming message used the term Viagra. The probability that the word Viagra was used in previous spam messages is called the likelihood and the probability that Viagra appeared in any message at all is known as the marginal likelihood.
By applying Bayes' theorem to this evidence, we can compute a posterior probability that measures how likely the message is to be spam. If the posterior probability is greater than 50 percent, the message is more likely to be spam than ham, and it should be filtered. The following formula is the Bayes' theorem for the given evidence:
To calculate the components of Bayes' theorem, we must construct a frequency table (shown on the left in the following diagram) that records the number of times Viagra appeared in spam and ham messages. Just like a two-way cross-tabulation, one dimension of the table indicates levels of the class variable (spam or ham), while the other dimension indicates levels for features (Viagra: yes or no). The cells then indicate the number of instances having the particular combination of class value and feature value. The frequency table can then be used to construct a likelihood table, as shown on right in the following diagram:

The likelihood table reveals that P(Viagra|spam) = 4/20 = 0.20, indicating that the probability is 20 percent that a spam message contains the term Viagra. Additionally, since the theorem says that P(B|A) * P(A) = P(A ∩ B), we can calculate P(spam ∩ Viagra) as P(Viagra|spam) * P(spam) = (4/20) * (20/100) = 0.04. This is four times greater than the previous estimate under the faulty independence assumption illustrating the importance of Bayes' theorem when calculating joint probability.
To compute the posterior probability, P(spam|Viagra), we simply take P(Viagra|spam) * P(spam) / P(Viagra), or (4/20) * (20/100) / (5/100) = 0.80. Therefore, the probability is 80 percent that a message is spam, given that it contains the word Viagra. Therefore, any message containing this term should be filtered.
This is very much how commercial spam filters work, although they consider a much larger number of words simultaneously when computing the frequency and likelihood tables. In the next section, we'll see how this concept is put to use when additional features are involved.
The naive Bayes (NB) algorithm describes a simple application using Bayes' theorem for classification. Although it is not the only machine learning method utilizing Bayesian methods, it is the most common, particularly for text classification where it has become the de facto standard. Strengths and weaknesses of this algorithm are as follows:
|
Strengths |
Weaknesses |
|---|---|
The naive Bayes algorithm is named as such because it makes a couple of "naive" assumptions about the data. In particular, naive Bayes assumes that all of the features in the dataset are equally important and independent. These assumptions are rarely true in most of the real-world applications.
For example, if you were attempting to identify spam by monitoring email messages, it is almost certainly true that some features will be more important than others. For example, the sender of the email may be a more important indicator of spam than the message text. Additionally, the words that appear in the message body are not independent from one another, since the appearance of some words is a very good indication that other words are also likely to appear. A message with the word Viagra is probably likely to also contain the words prescription or drugs.
However, in most cases when these assumptions are violated, naive Bayes still performs fairly well. This is true even in extreme circumstances where strong dependencies are found among the features. Due to the algorithm's versatility and accuracy across many types of conditions, naive Bayes is often a strong first candidate for classification learning tasks.
Tip
The exact reason why naive Bayes works well in spite of its faulty assumptions has been the subject of much speculation. One explanation is that it is not important to obtain a careful estimate of probability so long as the predicted class values are true. For instance, if a spam filter correctly identifies spam, does it matter that it was 51 percent or 99 percent confident in its prediction? For more information on this topic, refer to On the optimality of the simple Bayesian classifier under zero-one loss in Machine Learning, by Pedro Domingos and Michael Pazzani (1997).
Let's extend our spam filter by adding a few additional terms to be monitored: money, groceries, and unsubscribe. The naive Bayes learner is trained by constructing a likelihood table for the appearance of these four words (W1, W2, W3, and W4), as shown in the following diagram for 100 emails:

As new messages are received, the posterior probability must be calculated to determine whether they are more likely spam or ham, given the likelihood of the words found in the message text. For example, suppose that a message contains the terms Viagra and Unsubscribe, but does not contain either Money or Groceries.
Using Bayes' theorem, we can define the problem as shown in the following formula, which captures the probability that a message is spam, given that Viagra = Yes, Money = No, Groceries = No, and Unsubscribe = Yes:

For a number of reasons, this formula is computationally difficult to solve. As additional features are added, tremendous amounts of memory are needed to store probabilities for all of the possible intersecting events; imagine the complexity of a Venn diagram for the events for four words, let alone for hundreds or more. Enormous training datasets would be required to ensure that enough data is available to model all of the possible interactions.
The work becomes much easier if we can exploit the fact that naive Bayes assumes independence among events. Specifically, naive Bayes assumes class-conditional independence, which means that events are independent so long as they are conditioned on the same class value. Assuming conditional independence allows us to simplify the formula using the probability rule for independent events, which you may recall is P(A ∩ B) = P(A) * P(B). This results in a much easier-to-compute formulation, shown as follows:

The result of this formula should be compared to the probability that the message is ham:

Using the values in the likelihood table, we can start filling numbers in these equations. Because the denominator is the same in both cases, it can be ignored for now. The overall likelihood of spam is then:
(4/20) * (10/20) * (20/20) * (12/20) * (20/100) = 0.012
While the likelihood of ham given this pattern of words is:
(1/80) * (66/80) * (71/80) * (23/80) * (80/100) = 0.002
Because 0.012 / 0.002 = 6, we can say that this message is six times more likely to be spam than ham. However, to convert these numbers to probabilities, we need one last step.
The probability of spam is equal to the likelihood that the message is spam divided by the likelihood that the message is either spam or ham:
0.012 / (0.012 + 0.002) = 0.857
Similarly, the probability of ham is equal to the likelihood that the message is ham divided by the likelihood that the message is either spam or ham:
0.002 / (0.012 + 0.002) = 0.143
Given the pattern of words in the message, we expect that the message is spam with 85.7 percent probability, and ham with 14.3 percent probability. Because these are mutually exclusive and exhaustive events, the probabilities sum up to one.
The naive Bayes classification algorithm we used in the preceding example can be summarized by the following formula. Essentially, the probability of level L for class C, given the evidence provided by features F 1 through F n, is equal to the product of the probabilities of each piece of evidence conditioned on the class level, the prior probability of the class level, and a scaling factor 1 / Z, which converts the result to a probability:
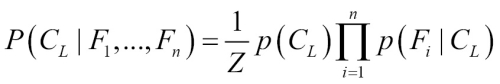
Let's look at one more example. Suppose we received another message, this time containing the terms: Viagra, Groceries, Money, and Unsubscribe. Using the naive Bayes algorithm as before, we can compute the likelihood of spam as:
(4/20) * (10/20) * (0/20) * (12/20) * (20/100) = 0
And the likelihood of ham is:
(1/80) * (14/80) * (8/80) * (23/80) * (80/100) = 0.00005
Therefore, the probability of spam is:
0 / (0 + 0.0099) = 0
And the probability of ham is:
0.00005 / (0 + 0. 0.00005) = 1
These results suggest that the message is spam with 0 percent probability and ham with 100 percent probability. Does this prediction make sense? Probably not. The message contains several words usually associated with spam, including Viagra, which is very rarely used in legitimate messages. It is therefore very likely that the message has been incorrectly classified.
This problem might arise if an event never occurs for one or more levels of the class. For instance, the term Groceries had never previously appeared in a spam message. Consequently, P(spam|groceries) = 0%.
Because probabilities in naive Bayes are multiplied, this 0 percent value causes the posterior probability of spam to be zero, giving the word Groceries the ability to effectively nullify and overrule all of the other evidence. Even if the email was otherwise overwhelmingly expected to be spam, the absence of the word Groceries will always result in a probability of spam being zero.
A solution to this problem involves using something called the Laplace estimator, which is named after the French mathematician Pierre-Simon Laplace. The Laplace estimator essentially adds a small number to each of the counts in the frequency table, which ensures that each feature has a nonzero probability of occurring with each class. Typically, the Laplace estimator is set to 1, which ensures that each class-feature combination is found in the data at least once.
Tip
The Laplace estimator can be set to any value, and does not necessarily even have to be the same for each of the features. If you were a devoted Bayesian, you could use a Laplace estimator to reflect a presumed prior probability of how the feature relates to the class. In practice, given a large enough training dataset, this step is unnecessary, and the value of 1 is almost always used.
Let's see how this affects our prediction for this message. Using a Laplace value of 1, we add one to each numerator in the likelihood function. The total number of 1s must also be added to each denominator. The likelihood of spam is therefore:
(5/24) * (11/24) * (1/24) * (13/24) * (20/100) = 0.0004
And the likelihood of ham is:
(2/84) * (15/84) * (9/84) * (24/84) * (80/100) = 0.0001
This means that the probability of spam is 80 percent and the probability of ham is 20 percent; a more plausible result than the one obtained when Groceries alone determined the result.
Because naive Bayes uses frequency tables for learning the data, each feature must be categorical in order to create the combinations of class and feature values comprising the matrix. Since numeric features do not have categories of values, the preceding algorithm does not work directly with numeric data. There are, however, ways that this can be addressed.
One easy and effective solution is to discretize numeric features, which simply means that the numbers are put into categories known as bins. For this reason, discretization is also sometimes called binning. This method is ideal when there are large amounts of training data, a common condition when working with naive Bayes.
There are several different ways to discretize a numeric feature. Perhaps the most common is to explore the data for natural categories or cut points in the distribution of data. For example, suppose that you added a feature to the spam dataset that recorded the time of night or day the email was sent, from 0 to 24 hours past midnight.
Depicted using a histogram, the time data might look something like the following diagram. In the early hours of morning, message frequency is low. Activity picks up during business hours, and tapers off in the evening. This seems to create four natural bins of activity, as partitioned by the dashed lines indicating places where the numeric data are divided into levels of a new nominal feature, which could then be used with naive Bayes:

Keep in mind that the choice of four bins was somewhat arbitrary, based on the natural distribution of data and a hunch about how the proportion of spam might change throughout the day. We might expect that spammers operate in the late hours of the night, or they may operate during the day, when people are likely to check their email. That said, to capture these trends, we could have just as easily used three bins or twelve.
One thing to keep in mind is that discretizing a numeric feature always results in a reduction of information, as the feature's original granularity is reduced to a smaller number of categories. It is important to strike a balance, since too few bins can result in important trends being obscured, while too many bins can result in small counts in the naive Bayes frequency table.
