APPENDIX F

Numerical Methods for Evaluating the Q-Function

In this appendix, we give an overview of several methods available for numerically evaluating the CDF of a Gaussian random variable and related integrals. Recall that for a zero-mean unit variance Gaussian random variable, the CDF is given by the integral

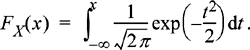(F.1)

The Q-function is the complement of this integral

(F.2)

Many math packages have internal routines for evaluating related integrals, usually the error function or complementary error function. Given the most common definitions of these functions,

(F.3)

(F.4)

the Q-function can then be written in terms of these functions as

(F.5)

For situations where internally defined functions are not available, several numerical techniques are available for efficiently evaluating the Q-function. To start with, recall the symmetry relationship

(F.6)

Hence any routine for evaluating the Q-function only needs to work on positive values of x. To start with, we consider the Taylor series expansion of the Q-function about the point x = 0,

(F.7)

This series is convergent for all x ≥ 0 but will converge faster for smaller values of x. A good approximation can be obtained by truncating the series to a sufficient number of terms. Since the series is alternating, the truncation error is bounded by the first term neglected. Figure F.1 shows the Q-function along with its approximations using the Taylor series truncated to various numbers of terms. It is seen from this figure that for x > 2, a large number of terms may be needed for the Taylor series to converge.

Figure F.1 The Q-function and its truncated Taylor series approximation.

For larger values of x, it is common to use the following asymptotic series expansion

(F.8)

Since the series has negative powers of x, the larger x is, the faster the series will converge. Also, as with the Taylor series expansion, since this is a convergent alternating series, the truncation error will be bounded by the first neglected term. Also, the sign of the error will be the same as that of the first neglected term. As a result, for large values of x, the Q-function can be upper and lower bounded by

(F.9)

These two bounds are shown in Figure F.2. From the figure as well as from the expressions in the previous equation, it is clear that as x →∞ both bounds are asymptotically tight. Hence it is seen that

(F.10)

Figure F.2 Upper and lower bounds on the Q-function.

From the figure, it appears that this approximation is fairly accurate for x > 4. If more accuracy is desired, more terms can be included in the asymptotic expansion.

In addition to the Taylor series and asymptotic series expansions, there are also a few continued fraction expansions for the Q-function. These are listed below:

(F.11)

(F.12)

A number of polynomial and rational approximations of the Q-function are available. Among them, the following seems to offer the best accuracy:

(F.13)

where,

p = 0.2316419,

b₁ = 0.319381530,

b₂ = −0.35656378,

b₃ = 1.7814779,

b₄ = −1.821256,

b₅ = 1.3302744.

The error in this approximation is less than 7.5 × 10⁻⁸ for all 0 ≤ x ≤ ∞.

Finally, we note that any desired accuracy can be obtained by computing the Q-function via numerical integration. Using the definition directly, the Q-function has an infinite limit which is inconvenient for performing numerical integration. For small to moderate values of x, this problem can be circumvented by rewriting the Q-function as

(F.14)

For large values of x it may be more efficient to work with the standard definition and truncate the upper limit to form the approximation

(F.15)

where the constant c is chosen to insure the desired accuracy. For c > 2 and x > 1.5 the relative error in this approximation can be shown to be bounded by

(F.16)

For example, choosing c = 3.5 will guarantee a relative accuracy of less than 10⁻⁴ (i.e., four digits of accuracy). Finally, we note an alternative form of the Q-function which has finite limits,

(F.17)

Since the integrand is fairly well behaved and the limits of integration are finite, numerical integration on this form is particularly convenient and can be performed to any desired accuracy.