Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

15.3 Control Charts for Variables

Control charts for the mean, $\bar{x},$ $\bar{x},$ and the range, R, are used to monitor processes that are measured in continuous units. Examples of these would be weight, height, and volume. The $\bar{x}$ $\bar{x}$ -chart (x-bar chart) tells us whether changes have occurred in the central tendency of a process. This might be due to such factors as tool wear, a gradual increase in temperature, a different method used on the second shift, or new and stronger materials. The R-chart values indicate that a gain or loss in uniformity has occurred. Such a change might be due to worn bearings, a loose tool part, an erratic flow of lubricants to a machine, or sloppiness on the part of a machine operator. The two types of charts go hand in hand when monitoring variables.

The Central Limit Theorem

The statistical foundation for $\bar{x}$ $\bar{x}$ -charts is the central limit theorem. In general terms, this theorem states that, regardless of the distribution of the population of all parts or services, the distribution of $\bar{x}$ $\bar{x}$ s (each of which is a mean of a sample drawn from the population) will tend to follow a normal curve as the sample size grows large. Fortunately, even if n is fairly small (say, 4 or 5), the distribution of the averages will still roughly follow a normal curve. The theorem also states that (1) the mean of the distribution of the $\bar{x}$ $\bar{x}$ -s (called $μ_{\bar{x}}$ $μ_{\bar{x}}$ ) will equal the mean of the overall population (called $μ$ $μ$ ) and (2) the standard deviation of the sampling distribution, $σ_{\bar{x}},$ $σ_{\bar{x}},$ will be the population deviation, $σ_{x},$ $σ_{x},$ divided by the square root of the sample size, n. In other words,

μ_{\bar{x}} = μ and σ_{\bar{x}} = \frac{σ_{x}}{\sqrt{n}}

$μ_{\bar{x}} = μ and σ_{\bar{x}} = \frac{σ_{x}}{\sqrt{n}}$

Although there may be times when we may know $μ_{\bar{x}}$ $μ_{\bar{x}}$ (and $μ$ $μ$ ), often we must estimate this with the average of all the sample means (written as $\bar{\bar{x}}$ $\bar{\bar{x}}$ ).

Figure 15.2 shows three possible population distributions, each with its own mean, $μ$ $μ$ , and standard deviation, $σ_{x} .$ $σ_{x} .$ If a series of random samples ( ${\bar{x}}_{1}, {\bar{x}}_{2}, {\bar{x}}_{3}, {\bar{x}}_{4},$ ${\bar{x}}_{1}, {\bar{x}}_{2}, {\bar{x}}_{3}, {\bar{x}}_{4},$ and so on), each of size n, is drawn from any one of these, the resulting distribution of ${\bar{x}}_{i}$ ${\bar{x}}_{i}$ s will appear as in the bottom graph of that figure. Because this is a normal distribution (as discussed in Chapter 2), we can state that

99.7% of the time, the sample averages will fall within $\pm 3 σ_{\bar{x}}$ $\pm 3 σ_{\bar{x}}$ of the population mean if the process has only random variations.
95.5% of the time, the sample averages will fall within $\pm 2 σ_{\bar{x}}$ $\pm 2 σ_{\bar{x}}$ of the population mean if the process has only random variations.

If a point on the control chart falls outside the $\pm 3 σ_{\bar{x}}$ $\pm 3 σ_{\bar{x}}$ control limits, we are 99.7% sure that the process has changed. This is the theory behind control charts.

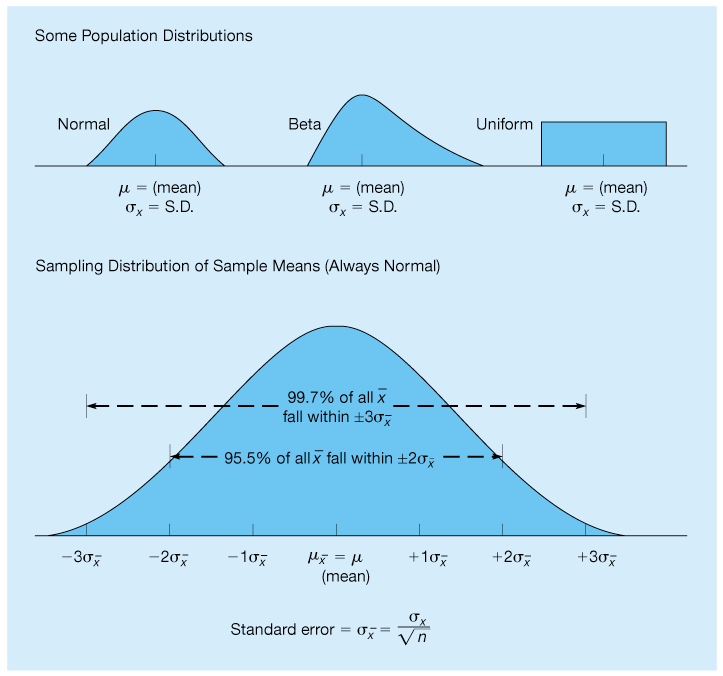
Figure illustrates 3 population distributions and a sampling distribution. — Figure 15.2 Population and Sampling Distributions

Figure 15.2 Full Alternative Text

Modeling In The Real World Hospital Uses Quality Control Analytics to Improve Business Process

Defining the Problem

The billing process at a medium-sized hospital were taking far too long. The long cycle times from care performed to payment received were identified as the root cause of missed payments, upset patients, and headaches for the accounts receivable department of the hospital.

Developing a Model

Hospital managers turned to quality control analytics to reduce the cycle times. In particular, they looked to a Six Sigma technique known as Define-Measure-Analyze-Improve-Control (DMAIC).

Acquiring Input Data

A project team was formed, and the members began to work on the problem. They first modeled the “as-is” business process of patient billing with a flowchart. This allowed the team to see where potential bottlenecks in the process were. Average times for each task in the flowchart were captured and examined.

Developing a Solution

Team members developed alternative processes for some existing ones (e.g., email instead of hard copy), eliminated some existing procedures (e.g., deleting unnecessary approval signatures on forms), and re-designed the entire process from care performed to payment received.

Testing the Solution

A critical path analysis was performed on the “as-is” billing process, as well as the newly designed “to-be” billing process. This allowed the team members to test their solution alongside the existing process.

Analyzing the Results

The critical path analysis also led the team to identify a task within the process (i.e., price acquisition) that had no immediate predecessors but was the cause of many long billing cycles. The team was able to “move” this task to the beginning of the process.

Implementing the Results

Hospital management installed the new business process. The result was a billing process that was an entire month shorter and saved the hospital some 390,000 euros annually.

Source: Based on M. Schoonhoven, C. Lubbers, and R. J. M. M. Does, “Quality Quandaries: Shortening the Throughput Time of a Hospital’s Billing Process,” Quality Engineering 25 (2013): 188–193, © Trevor S. Hale.

Setting X -Chart Limits

If we know through historical data the standard deviation of the process population, $σ_{x},$ $σ_{x},$ we can set upper and lower control limits by these formulas:

Upper control limit (UCL) = \bar{\bar{x}} + z σ_{\bar{x}}

$Upper control limit (UCL) = \bar{\bar{x}} + z σ_{\bar{x}}$ (15-1)

Lower control limit (LCL) = \bar{\bar{x}} - z σ_{\bar{x}}

$Lower control limit (LCL) = \bar{\bar{x}} - z σ_{\bar{x}}$ (15-2)

where

$\bar{\bar{x}} =$ $\bar{\bar{x}} =$ mean of the sample means
$z =$ $z =$ number of normal standard deviations (2 for 95.5% confidence, 3 for 99.7%)
$σ_{\bar{x}} =$ $σ_{\bar{x}} =$ standard deviation of the sampling distribution of the sample means $= \frac{σ_{x}}{\sqrt{n}}$ $= \frac{σ_{x}}{\sqrt{n}}$

Box-Filling Example

Let us say that a large production lot of boxes of cornflakes is sampled every hour. To set control limits that include 99.7% of the sample means, 36 boxes are randomly selected and weighed. The standard deviation of the overall population of boxes is estimated, through analysis of old records, to be 2 ounces. The average mean of all samples taken is 16 ounces. We therefore have $\bar{\bar{x}} = 16$ $\bar{\bar{x}} = 16$ ounces, $σ_{x} = 2$ $σ_{x} = 2$ ounces, $n = 36,$ $n = 36,$ and $z = 3.$ $z = 3.$ The control limits are

\begin{array}{l} {UCL}_{\bar{x}} & = & \bar{\bar{x}} + z σ_{\bar{x}} = 16 + 3 (\frac{2}{\sqrt{36}}) = 16 + 1 = 17 ounces \\ {LCL}_{\bar{x}} & = & \bar{\bar{x}} + z σ_{\bar{x}} = 16 - 3 (\frac{2}{\sqrt{36}}) = 16 - 1 = 15 ounces \end{array}

$\begin{array}{l} {UCL}_{\bar{x}} & = & \bar{\bar{x}} + z σ_{\bar{x}} = 16 + 3 (\frac{2}{\sqrt{36}}) = 16 + 1 = 17 ounces \\ {LCL}_{\bar{x}} & = & \bar{\bar{x}} + z σ_{\bar{x}} = 16 - 3 (\frac{2}{\sqrt{36}}) = 16 - 1 = 15 ounces \end{array}$

If the process standard deviation is not available or is difficult to compute, which is usually the case, these equations become impractical. In practice, the calculation of control limits is based on the average range rather than on standard deviations. We can use the equations

{UCL}_{\bar{x}} = \bar{\bar{x}} + A_{2} \bar{R}

${UCL}_{\bar{x}} = \bar{\bar{x}} + A_{2} \bar{R}$ (15-3)

{LCL}_{\bar{x}} = \bar{\bar{x}} - A_{2} \bar{R}

${LCL}_{\bar{x}} = \bar{\bar{x}} - A_{2} \bar{R}$ (15-4)

where

$\bar{R} =$ $\bar{R} =$ average of the samples
$A_{2} =$ $A_{2} =$ value found in Table 15.2 (which assumes that $z = 3$ $z = 3$ )
$\bar{\bar{x}} =$ $\bar{\bar{x}} =$ mean of the sample means

Table 15.2 Factors for Computing Control Chart Limits When $z = 3$ $z = 3$

Sample Size, n	Mean Factor, $A_{2}$ $A_{2}$	Upper Range, $D_{4}$ $D_{4}$	Lower Range, $D_{3}$ $D_{3}$
2	1.880	3.268	0
3	1.023	2.574	0
4	0.729	2.282	0
5	0.577	2.114	0
6	0.483	2.004	0
7	0.419	1.924	0.076
8	0.373	1.864	0.136
9	0.337	1.816	0.184
10	0.308	1.777	0.223
12	0.266	1.716	0.284
14	0.235	1.671	0.329
16	0.212	1.636	0.364
18	0.194	1.608	0.392
20	0.180	1.586	0.414
25	0.153	1.541	0.459
Source: Reprinted, with permission, from Special Technical Publication 15-C, “Quality Control of Materials,” pp. 63 and 72, © American Society for Testing and Materials International, 100 Barr Harbor Drive, West Conshochocken, PA 19428.

Using Excel QM For Box-Filling Example

The upper and lower limits for this example can be found using Excel QM, as shown in Program 15.1. From the Excel QM menu, select Quality Control and specify the X-Bar and R Chartsoption. Enter the number of samples (1) and select Standard Deviation in the initialization window. When the spreadsheet is initialized, enter the sample size (36), the standard deviation (2), and the mean of the sample (16). The upper and lower limits are immediately displayed.

A screenshot of a spreadsheet represents the Excel QM solution for box-filling example. — Program 15.1 Excel QM Solution for Box-Filling Example

Figure 15.1 Full Alternative Text

Super Cola Example

Super Cola bottles soft drinks labeled “net weight 16 ounces.” An overall process average of 16.01 ounces has been found by taking several batches of samples, in which each sample contained five bottles. The average range of the process is 0.25 ounce. We want to determine the upper and lower control limits for averages for this process.

Looking in Table 15.2 for a sample size of 5 in the mean factor $A_{2}$ $A_{2}$ column, we find the number 0.577. Thus, the upper and lower control chart limits are

\begin{array}{l} {UCL}_{\bar{x}} & = & \bar{\bar{X}} + A_{2} \bar{R} \\ = & 6.01 + (0.577) (0.25) \\ = & 16.01 + 0.144 \\ = & 16.154 \\ {LCL}_{\bar{x}} & = & \bar{\bar{X}} - A_{2} \bar{R} \\ = & 16.01 - 0.144 \\ = & 15.866 \end{array}

$\begin{array}{l} {UCL}_{\bar{x}} & = & \bar{\bar{X}} + A_{2} \bar{R} \\ = & 6.01 + (0.577) (0.25) \\ = & 16.01 + 0.144 \\ = & 16.154 \\ {LCL}_{\bar{x}} & = & \bar{\bar{X}} - A_{2} \bar{R} \\ = & 16.01 - 0.144 \\ = & 15.866 \end{array}$

The upper control limit is 16.154, and the lower control limit is 15.866.

Using Excel QM For Super Cola Example

The upper and lower limits for this example can be found using Excel QM, as shown in Program 15.2. From the Excel QM menu, select Quality Control and specify the X-Bar and R Charts option. Enter the number of samples (1) and select Range in the initialization window. The sample size (5) can be entered in this initialization window or in the spreadsheet. When the spreadsheet is initialized, enter the range (0.25) and the mean of the sample (16.01). The upper and lower limits are immediately displayed.

Setting Range Chart Limits

We just determined the upper and lower control limits for the process average. In addition to being concerned with the process average, managers are interested in the dispersion or variability. Even though the process average is under control, the variability of the process may not be. For example, something may have worked itself loose in a piece of equipment. As a result, the average of the samples may remain the same, but the variation within the samples could be entirely too large, and the x-bar charts could be unreliable. For this reason, it is necessary to find a control chart for ranges in order to monitor the process variability. The theory behind the control charts for ranges is the same as for the process average. Limits are established that contain $\pm 3$ $\pm 3$ standard deviations of the distribution for the average range $\bar{R} .$ $\bar{R} .$ With a few simplifying assumptions, we can set the upper and lower control limits for ranges:

{UCL}_{R} = D_{4} \bar{R}

${UCL}_{R} = D_{4} \bar{R}$ (15-5)

{LCL}_{R} = D_{3} \bar{R}

${LCL}_{R} = D_{3} \bar{R}$ (15-6)

A screenshot of a spreadsheet represents the Excel QM solution for Super Cola example. — Program 15.2 Excel QM Solution for Super Cola Example

Figure 15.2 Full Alternative Text

where

${UCL}_{R} = upper control chart limit for the range$ ${UCL}_{R} = upper control chart limit for the range$
${LCL}_{R} = lower control chart limit for the range$ ${LCL}_{R} = lower control chart limit for the range$
$D_{4} and D_{3} =$ $D_{4} and D_{3} =$ values from Table 15.2

Range Example

As an example, consider a process in which the average range is 53 pounds. If the sample size is five, we want to determine the upper and lower control chart limits.

Looking in Table 15.2 for a sample size of five, we find that $D_{4} = 2.114 and D_{3} = 0.$ $D_{4} = 2.114 and D_{3} = 0.$ The range control chart limits are

\begin{array}{l} {UCL}_{R} & = & D_{4} \bar{R} \\ = & (2.114) (53 pounds) \\ = & 112.042 pounds \\ {LCL}_{\bar{R}} & = & D_{3} \bar{R} \\ = & (0) (53 pounds) \\ = & 0 \end{array}

$\begin{array}{l} {UCL}_{R} & = & D_{4} \bar{R} \\ = & (2.114) (53 pounds) \\ = & 112.042 pounds \\ {LCL}_{\bar{R}} & = & D_{3} \bar{R} \\ = & (0) (53 pounds) \\ = & 0 \end{array}$

A summary of the stpng used for creating and using control charts for the mean and the range follows.

Five Stpng to Follow in Using X and R-Charts

Collect 20 to 25 samples of typically $n = 4 or n = 5$ $n = 4 or n = 5$ each from a stable process, and compute the mean and range of each.
Compute the overall means $\bar{\bar{x}}$ $\bar{\bar{x}}$ and $\bar{R}$ $\bar{R}$ ); set appropriate control limits, usually at the 99.7% level; and calculate the preliminary upper and lower control limits. If the process is not currently stable, use the desired mean, $μ,$ $μ,$ instead of $\bar{\bar{x}}$ $\bar{\bar{x}}$ to calculate limits.
Graph the sample means and ranges on their respective control charts, and determine whether they fall outside the acceptable limits.
Investigate points or patterns that indicate the process is out of control. Try to find an assignable cause for the out-of-control condition, address it accordingly, and then resume the process.
Collect additional samples and, if necessary, revalidate the control limits using the new data.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 15.3 Control Charts for Variables

Create new playlist

Sign In

Sign Up

Table of Contents for
15.3 Control Charts for Variables