CHAPTER 21

Exact, Metaheuristic, and Hybrid Approaches to Multidimensional Knapsack Problems

J. E. GALLARDO, C. COTTA, and A. J. FERNÁNDEZ

Universidad de Málaga, Spain

21.1 INTRODUCTION

In this chapter we review our recent work on applying hybrid collaborative techniques that integrate branch and bound (B&B) and memetic algorithms (MAs) in order to design effective heuristics for the multidimensional knapsack problem (MKP). To this end, let us recall that branch and bound (B&B) [102] is an exact algorithm for finding optimal solutions to combinatorial problems that works basically by producing convergent lower and upper bounds for the optimal solution using an implicit enumeration scheme. A different approach to optimization is provided by evolutionary algorithms (EAs) [2–4]. These are powerful heuristics for optimization problems based on principles of natural evolution: namely, adaptation and survival of the fittest. Starting from a population of randomly generated individuals (representing solutions), a process consisting of selection (promising solutions are chosen from the population), reproduction (new solutions are created by combining selected ones), and replacement (some solutions are replaced by new ones) is repeated. A fitness function measuring the quality of the solution is used to guide the process.

A key aspect of EAs is robustness, meaning that they can be deployed on a wide range of problems. However, it has been shown that some type of domain knowledge has to be incorporated into EAs for them to be competitive with other domain-specific optimization techniques [5–7]. A very successful approach to achieving this knowledge augmentation is to use memetic algorithms (MAs) [8–11], which integrate domain-specific heuristics into the EA. In this chapter, hybridizations of MAs with B&B are presented. The hybridizations are aimed at combining the search capabilities of both algorithms in a synergistic way.

The chapter is organized as follows. In the remainder of this section, general descriptions of branch and bound and memetic algorithms are given. In Section 21.2 the multidimensional knapsack problem is described along with branch and bound and a memetic algorithm to tackle it. Then in Section 21.3 we present our hybrid proposals integrating both approaches. Subsequently, in Section 21.4 we show and analyze the empirical results obtained by the application of each of the approaches described on different instances of the benchmark. Finally, in Section 21.5 we provide conclusions and outline ideas for future work.

21.1.1 Branch-and-Bound Algorithm

The branch-and-bound algorithm (B&B) is a very general exact technique, proposed by Land and Doig [12], that can be used to solve combinatorial optimization problems. B&B is basically an enumeration approach that prunes the nonpromising regions of the search space [102]. For this purpose, the algorithm uses two key ingredients: a branching rule, which provides a way of dividing a region of the search space into smaller regions (ideally, partitions of the original one), and a way to calculate an upper bound (assuming a maximization problem) on the best solution that can be attained in a region of the search space.

A very general pseudocode for this algorithm is shown in Algorithm 21.1. The algorithm maintains the best solution found so far (sol in the pseudocode), usually termed the incumbent solution. B&B starts by considering the entire search space of the problem (S). This is split into several subspaces (denoted by set C in the algorithm) using the branching rule. If a subspace is solved trivially and its value improves on the incumbent solution, the latter is updated. Otherwise, a bound for each subspace is calculated. If the bound of one subspace is worse than the incumbent solution, this part of the search space can safely be eliminated (this is called pruning). Otherwise, the process goes on until all subspaces are either solved or pruned, and the final value of the incumbent solution is returned as an optimal solution to the problem.

Algorithm 21.1 Branch-and-Bound Algorithm

The efficiency of the algorithm relies on the effectiveness of the branching rule and the accuracy of the bounds. If these ingredients of the algorithm are not well defined, the technique degenerates into an exhaustive inefficient search. On one side, an effective branching rule will avoid revisiting the same regions of the search space. One the other side, tight bounds will allow more pruning. Usually, it is difficult to find tight bounds that are not too expensive computationally, and a balance has to be found between the amount of pruning achieved and the computational complexity of the bounds. In any case, these techniques cannot practically be used on large instances for many combinatorial optimization problems (COPs).

Note that the search performed by the algorithm can be represented as a tree traversed in a certain way (which depends on the order in which subspaces are introduced and extracted in set open). If a depth-first strategy is used, the memory required grows linearly with the depth of the tree; hence, large problems can be considered. However, the time consumption can be excessive. On the other hand, a best-first strategy minimizes the number of nodes explored, but the size of the search tree (i.e., the number of nodes kept for latter expansion) will grow exponentially in general. A third option is to use a breadth-first traversal (i.e., every node in a level is explored before moving on to the next). In principle, this option would have the drawbacks of the preceding two strategies unless a heuristic choice is made: to keep at each level only the best nodes (according to some quality measure). This implies sacrificing exactness but provides a very effective heuristic search approach. The term beam search (BS) has been coined to denote this strategy [13, 14]. As such, BS algorithms are incomplete derivatives of B&B algorithms and are thus heuristic methods. A generic description of BS is depicted in Algorithm 21.2. Essentially, BS works by extending every partial solution from a set (called the beam) in all possible ways. Each new partial solution so generated is stored in a set ′. When all solutions in have been processed, the algorithm constructs a new beam by selecting the best up to k_bw (called the beam width) solutions from ′. Clearly, a way of estimating the quality of partial solutions, such as an upper bound or an heuristic, is needed for this.

One context in which B&B is frequently used is integer programming (IP) [15]. IP is a generalization of linear programming (LP) [16], so let us first describe the latter problem. In LP there are decision variables, constraints, and an objective function. Variables take real values, and both the objective function and the constraints must be expressed as a series of linear expressions in the decision variables. The goal is to find an assignment for the variables maximizing (or minimizing) the objective function. Linear programs can be used to model many practical problems, and nowadays, solvers can find optimal solutions to problems with hundred of thousands of constraints and variables in reasonable time. The first algorithm proposed to solve LPs was the simplex method devised by Dantzig in 1947 [17], which performs very well in practice, although its performance is exponential in the worst case. Afterward, other methods that run in polynomial time have been proposed, such as interior points methods [18]. In practice, the simplex algorithm works very well in most cases; other approaches are only useful for very large instances.

Algorithm 21.2 Beam Search Algorithm

An integer program is a linear program in which some or all variables are restricted to take integer values. This small change in the formulation increases considerably the number of problems that can be modeled, but also increases dramatically the difficulty of solving problems. One approach to solving IPs is to use a B&B algorithm that uses solutions to linear relaxations as bounds. These LP relaxations are obtained by removing the integral requirements on decision variables and can be solved efficiently using any LP method. Assuming a maximization problem, it follows that a solution to its LP relaxation is an upper bound for the solution of the original problem. In order to branch, the search space is usually partitioned into two parts by choosing an integer variable x_i that has fractional value in the LP-relaxed solution, and introducing two branches with the additional constraints and . One common heuristic is to choose as a branching variable the one with fractional part closest to 0.5, although commercial IP solvers use more sophisticated techniques.

21.1.2 Memetic Algorithms

The need to exploit problem knowledge in heuristics has been shown repeatedly in theory and in practice [5–7, 19]. Different attempts have been made to answer this need; memetic algorithms [8–11] (MAs) have probably been among the most successful to date [20].

The adjective memetic comes from the term meme, coined by Dawkins [21] to denote an analogy to the gene in the context of cultural evolution. As evolutionary algorithms, MAs are also population-based metaheuristics. The main difference is that the components of the population (called agents in the MAs terminology) are not passive entities. The agents are active entities that cooperate and compete in order to find improved solutions.

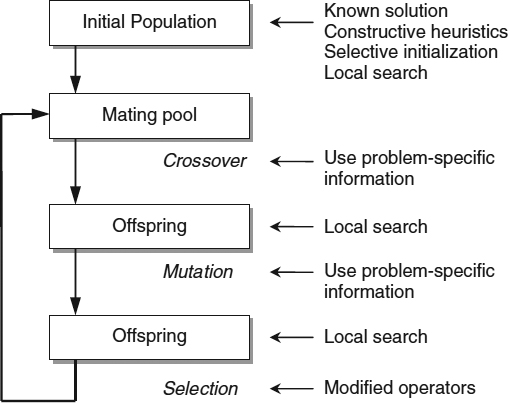
There are many possible ways to implement MAs. The most common implementation consists of combining an EA with a procedure to perform a local search that is usually done after evaluation, although it must be noted that the MA paradigm does not simply reduce itself to this particular scheme. According to Eiben and Smith [4], Figure 21.1 shows places were problem-specific knowledge can be incorporated. Some of the possibilities are:

• During the initialization of the population, some heuristic method may be used to generate high-quality initial solutions. One example of this type of technique is elaborated in this chapter: use of a variant of a B&B algorithm to initialize the population of a MA periodically, with the aim of improving its performance.
• Recombination or mutation operators can be designed intelligently so that specific problem knowledge is used to improve offspring.

Figure 21.1 Places to incorporate problem knowledge within an evolutionary algorithm, according to Eiben and Smith [4].

• Problem knowledge can be incorporated in the genotype-to-phenotype mapping present in many EAs, such as when repairing an nonfeasible solution. This technique is used in the MA designed by Chu and Beasley [22] for the MKP described in Section 21.2.3.

In addition to other domains, MAs have proven very successful across a wide range of combinatorial optimization problems, where they are state-of-the-art approaches for many problems. For a comprehensive bibliography, the reader is referred to [23, 24].

21.2 MULTIDIMENSIONAL KNAPSACK PROBLEM

In this section we review B&B algorithms and a memetic algorithm that have been proposed to tackle the MKP. Let us first introduce the problem.

21.2.1 Description of the Problem

The multidimensional knapsack problem (MKP) is a generalization of the classical knapsack problem (KP). In the KP, there is a knapsack with an upper weight limit b and a collection of n items with different values p_j and weights r_j. The problem is to choose the collection of items that gives the highest total value without exceeding the weight limit of the knapsack.

In the MKP, m knapsacks with different weight limits b_i must be filled with the same items. Furthermore, these items have a different weight r_ij for each knapsack i. The objective is to find a set of objects with maximal profit such that the capacity of the knapsacks is not exceeded. Formally, the problem can be formulated as:

where x is an nary binary vector such that x_j = 1 if the ith object is included in the knapsacks, and 0 otherwise.

Each of the m constraints in Equation 21.2 is called a knapsack constraint. The problem can be seen as a general statement of any 0–1 integer programming problem with nonnegative coefficients. Many practical problems can be formulated as an instance of the MKP: for example, the capital budgeting problem, project selection and capital investment, budget control, and numerous loading problems (see, e.g., ref. 25).

Although the classical knapsack problem is weakly NP-hard and admits a fully polynomial time approximation scheme (FPTAS) [26], this is not the case for the MKP, which is much more difficult, even for m = 2, and does not admit a FPTAS unless P = NP [27]. On the other hand, there exists a polynomial time approximation scheme (PTAS) with a running time of [28, 29], which implies a nonpolynomial increase in running time with respect to the accuracy sought.

21.2.2 Branch-and-Bound Algorithms for the MKP

As stated earlier, a complete solution for an instance of the MKP with n objects will be represented by an nary binary vector υ such that υ_i = 1 if the ith object is included in the solution, or 0 otherwise. The natural way of devising a B&B algorithm for the MKP is to start with a totally unspecified solution (a solution for which the inclusion or exclusion of any object is unknown), and to progressively fix the state of each object. This will lead to a branching rule that generates two new nodes from each partial node in the B&B tree by including or excluding a new object in the corresponding solution.

A way of estimating an upper bound for partial solutions is needed so that nonpromising partial solutions can be eliminated from the B&B queue. For this purpose we consider two possibilities. In the first, when the jth object is included in the solution, the lower bound for this partial solution is increased with the corresponding profit p_j (and the remaining available space is decreased by r_ij in each knapsack i), whereas the upper bound is decreased by p_j when the item is excluded. The second possibility is to carry out a standard LP exploration of the search tree for this type of problem, as described in Section 21.1.1 (see also ref. 30). More precisely, the linear relaxation of each node is solved (i.e., the problem corresponding to unfixed variables is solved, assuming that variables can take fractional values in the interval [0, 1]) using linear programming (LP) techniques such as the simplex method [17]. If all variables take integral values, the subproblem is solved. This is not generally the case, though, and some variables are noninteger in the LP-relaxed solution; in the latter situation, the variable whose value is closest to 0.5 is selected, and two subproblems are generated, fixing this variable at 0 or 1, respectively. The LP-relaxed value of the node is used as its upper bound, so that nodes whose value is below the best-known solution can be pruned from the search tree.

21.2.3 Chu and Beasley's MA for the MKP

In many studies (e.g., refs. 22 and 31–35) the MKP has been tackled using EAs. Among these, the EA developed by Chu and Beasley [22] remains a cutting-edge approach to solving the MKP. This EA uses the natural codification of solutions: namely, binary n-dimensional strings representing the incidence vector of a subset S of objects on the universal set O [i.e., (x_j = 1) ⇔ o_j ∈ S].

Of course, infeasible solutions might be encoded in this way, and this has to be considered in the EA. Typically, these situations can be solved in three ways: (1) allowing the generation of infeasible solutions and penalizing accordingly, (2) using a repair mechanism for mapping infeasible solutions to feasible solutions, and (3) defining appropriate operators and/or problem representation to avoid the generation of infeasible solutions. Chu and Beasley's approach is based on the second solution, that is, a Lamarckian repair mechanism is used (see ref. 36 for a comparison of Lamarckian and Baldwinian repair mechanisms for the MKP). To do so, an initial preprocessing of the problem instance is performed off-line. The goal is to obtain a heuristic precedence order among variables: They are ordered by decreasing pseudoutility values: , where we set the surrogate multipliers a_i to the dual variable values of the solution of the LP relaxation of the problem (see ref. 22 for details). Variables near the front of this ordered list are more likely to be included in feasible solutions (and analogously, variables near the end of the list are more likely to be excluded from feasible solutions). More precisely, whenever a nonfeasible solution is obtained, variables are set to zero in increasing order of pseudoutility until feasibility is restored. After this, feasible solutions are improved by setting variables to 1 in decreasing order of pseudoutility (as long as no constraint is violated). In this way, the repairing algorithm can actually be regarded as a (deterministic) local improvement procedure, and hence this EA certainly qualifies as a MA. Since this MA just explores the feasible portion of the search space, the fitness function can readily be defined as .

21.3 HYBRID MODELS

In this section we present hybrid models that integrate an MA with the B&B method. Our aim is to combine the advantages of the two approaches while avoiding (or at least minimizing) their drawbacks when working alone. First, in the following subsection, we discuss briefly some related literature regarding the hybridization of exact techniques and metaheuristics.

21.3.1 Hybridizing Exact and Metaheuristic Techniques

Although exact and heuristics methods are two very different ways of tacking COPs, they can be combined in hybrid approaches with the aim of combining their characteristics synergistically. This has been recognized by many researchers, and as a result, many proposals have emerged in recent years. Some authors have reviewed and classified the literature on this topic.

Dumitrescu and Stutzle's [37] classification of algorithms combines local search and exact methods. They focus on hybrid algorithms in which exact methods are used to strengthen local search.

Fernandez and Lourenço's [38] extensive compendium of exact and metaheuristics hybrid approaches for different COPs includes mixed-integer programming, graph coloring, frequency assignment, partitioning, maximum independent sets, maximum clique, traveling salesman, vehicle routing, packing, and job shop scheduling problems.

Puchinger and Raidl's [39] classification of exact and metaheuristics hybrid techniques is possibly the most general. There are two main categories in their classification: collaborative and integrative combinations. In the following we describe each one in detail.

Collaborative Combinations This class includes hybrid algorithms in which the exact and metaheuristic methods exchange information but neither is a subordinate of the other. As both algorithms have to be executed, two cases can be considered:

1. Sequential execution, in which one of the algorithms is completely executed before the other. For example, one technique can act as a kind of preprocessing for the other, or the result of one algorithm can be used to initialize the other.
2. Parallel or intertwined execution, where the two techniques are executed simultaneously, either in parallel (i.e., running at the same time on different processors) or in an intertwined way by alternating between the two algorithms.

One example in the first group is the hybrid algorithm proposed by Vasquez and Hao [40] to tackle the MKP, which combines linear programming and tabu search. Their central hypothesis is that the neighborhood of a solution to a relaxed version of a problem contains high-quality solutions to the original problem. They use a two-phase algorithm that first solves exactly a relaxation of the problem, and afterward explores its neighborhood carefully and efficiently. For the first phase, they use the simplex method; for the second they use a tabu search procedure. This hybrid algorithm produces excellent results for large and very large instances of a problem.

An example of parallel execution is presented by Denzinger and Offermann [41]. It is based on a multiagent model for obtaining cooperation between search systems with different search paradigms. The basic schema consisted of teams with a number of agents subjected to the same search paradigm that exchanged a certain class of information. To demonstrate the feasibility of the approach, a GA- and B&B-based system for a job shop scheduling problem was described. Here, the GA and B&B agents only exchanged information in the form of solutions, whereas the B&B agents could also exchange information in the form of closed subtrees. As a result of the cooperation, better solutions were found given a timeout.

In this chapter we present proposals in the second group: namely, hybridizations of a B&B variant (e.g., using depth-first strategy or a beam search algorithm) and a memetic algorithm that are executed in an intertwined way.

Integrative Combinations Here, one technique uses the other for some purpose; the first acts as a master while the second behaves as a subordinate of the first. Again, two cases may be considered. The first consists of incorporating an exact algorithm into a metaheuristic. One example is the MA for the MKP by Chu and Beasley [22] (described in detail in Section 21.2.3).

Cotta and Troya [42] presented a framework for hybridization along the lines initially sketched by Cotta et al. [43] (i.e., based on using the B&B algorithm as a recombination operator embedded in the EA). This hybrid operator is used for recombination: It intelligently explores the possible children of solutions being recombined, providing the best possible outcome. The resulting hybrid algorithm provided better results than those of pure EAs in several problems where a full B&B exploration was not practical on its own.

Puchinger et al. [44] presented another attempt to incorporate exact methods in metaheuristics. This work considered different heuristics algorithms for a real-world glass-cutting problem, and a combined GA and B&B approach was proposed. The GA used an order-based representation that was decoded with a greedy heuristic. Incorporating B&B in the decoding for occasional (with a certain probability) locally optimizing subpatterns turned out to increase the solution quality in a few cases.

The other possibility for integrative combinations is to incorporate a metaheuristics into an exact algorithm. One example is a hybrid algorithm that combines genetic algorithms and integer programming B&B approaches to solve the MAX-SAT problems described by French et al. [45]. This hybrid algorithm gathered information during the run of a linear programming–based B&B algorithm and used it to build the population of an EA population. The EA was eventually activated, and the best solution found was used to inject new nodes in the B B search tree. The hybrid algorithm was run until the search tree was exhausted; hence, it is an exact approach. However, in some cases it expands more nodes than does the B B algorithm alone. A different approach has been put forth recently [46] in which a metaheuristic is used for strategic guidance of an exact B&B method. The idea was to use a genetic programming (GP) model to obtain improved node selection strategies within B&B for solving mixed-integer problems. The information collected from the B&B after operating for a certain amount of time is used as a training set for GP, which is run to find a node selection strategy more adequate for the specific problem. Then a new application of the B&B used this improved strategy. The idea was very interesting, although it is not mature and requires further research to obtain more general conclusions.

Cotta et al. [43] used a problem-specific B&B approach to the traveling salesman problem based on 1-trees and Lagrangean relaxation [47], and made use of an EA to provide bounds to guide the B&B search. More specifically, two different approaches to integration were analyzed. In the first model, the genetic algorithm played the role of master and the B&B was incorporated as a slave. The primary idea was to build a hybrid recombination operator based on the B&B philosophy. More precisely, B&B was used to build the best possible tour within the (Hamiltonian) subgraph defined by the union of edges in the parents. This recombination procedure was costly but provided better results than did a blind edge recombination. The second model proposed consisted of executing the B&B algorithm in parallel with a certain number of EAs, which generated a number of different high-quality solutions. The diversity provided by the independent EAs contributed to making edges suitable to be part of the optimal solution that were probably included in some individuals, and nonsuitable edges were unlikely to be taken into account. Despite the fact that these approaches showed promise, the work described by Cotta et al. [43] showed only preliminary results.

21.3.2 Hybrid Proposals

One way to integrate evolutionary techniques and B&B models is through direct collaboration, which consists of letting both techniques work alone in parallel (i.e., letting both processes perform independently), that is, at the same level. The two processes will share the solution. There are two ways of obtaining the benefit of this parallel execution:

1. The B&B can use the lower bound provided by the EA to purge the problem queue, deleting those problems whose upper bound is smaller than the one obtained by the EA.
2. The B&B can inject information about more promising regions of the search space into the EA population to guide the EA search.

In our hybrid approach, a single solution is shared among the EA and B&B algorithms that are executed in an interleaved way. Whenever one of the algorithms finds a better approximation, it updates the solution and yields control to the other algorithm.

Two implementation of this scheme are considered. In the first [48], the hybrid algorithm starts by running the EA to obtain a first approximation to the solution. In this initial phase, the population is initialized randomly and the EA executed until the solution is not improved for a certain number of iterations. This approximation can later be used by the B&B algorithm to purge the problem queue. No information from the B&B algorithm is incorporated in this initial phase of the EA, to avoid the injection of high-valued building blocks that could affect diversity, polarizing further evolution.

Afterward, the B&B algorithm is executed. Whenever a new solution is found, it is incorporated into the EA population (replacing the worst individual), the B&B phase is paused, and the EA is run to stabilization. Periodically, pending nodes in the B&B queue are incorporated into the EA population. Since these are partial solutions and the EA population consists of full solutions, they are completed and corrected using the repair operator. The intention of this transfer is to direct the EA to these regions of the search space. Recall that the nodes in the queue represent the subset of the search space still unexplored. Hence, the EA is used to find probably good solutions in this region. Upon finding an improved lower bound (or upon stabilization of the EA, in case no improvement is found), control is returned to the B&B, hopefully with an improved lower bound. This process is repeated until the search tree is exhausted or a time limit is reached. The hybrid is then an anytime algorithm that provides both a quasioptimal solution and an indication of the maximum distance to the optimum. One interesting peculiarity of BS is that it works by extending in parallel a set of different partial solutions in several possible ways. For this reason, BS is a particularly suitable tree search method to be used in a hybrid collaborative framework, as it can be used to provide periodically diverse promising partial solutions to a population-based search method such as an MA. We have used exactly this approach in our second implementation [49, 50], and a general description of the resulting algorithm is given in Algorithm 21.3.

The algorithm begins by executing BS for l₀ levels of the search tree. Afterward, the MA and BS are interleaved until a termination condition is reached. Every time the MA is run, its population is initialized using the nodes in the BS queue. Usually, the size of the BS queue will be larger than the MA population size, so some criteria must be used to select a subset from the queue. For instance, these criteria may be selecting the best nodes according to some measure of quality or selecting a subset from the BS queue that provides high diversity. Note that nodes in the BS queue represent schemata (i.e., they are partial solutions in which some genes are fixed but others are indeterminate), so they must first be converted to full solutions in a problem-dependent way. This is another aspect that must be considered when instantiating a general schema for various combinatorial problems.

Upon stabilization of the MA, control is returned to the B&B algorithm. The lower bound for the optimal solution obtained by the MA is then compared to the current incumbent in the B&B, updating the latter if necessary. This may lead to new pruned branches in the BS tree. Subsequently, BS is executed for descending l levels of the search tree. This process is repeated until the search tree is exhausted or a time limit is reached.

Algorithm 21.3 General Description of the Hybrid Algorithm

21.4 EXPERIMENTAL ANALYSIS

We tested our algorithms with problems available at the OR library [51] maintained by Beasley. We took two instances per problem set. Each problem set is characterized by a number m of constraints (or knapsacks), a number n of items, and a tightness ratio, 0 ≤ α ≤ 1. The closer to 0 the tightness ratio is, the more constrained the instance. All algorithms were coded in C, and all tests were carried out on a Pentium-4 PC (1700 MHz and 256 Mbytes of main memory).

21.4.1 Results for the First Model

In this section we describe the results obtained by the first hybrid model described in Section 21.3.2. The B&B algorithm explores the search tree in a depth-first way and uses the first simple upper bound described in Section 21.2.2. A single execution for each instance was performed for the B&B methods, whereas 10 runs were carried out for the EA and hybrid algorithms. The algorithms were run for 600 seconds in all cases. For the EA and the hybrid algorithm, population size was fixed at 100 individuals, initialized with random feasible solutions. Mutation probability was set at 2 bits per string, recombination probability at 0.9, a binary tournament selection method was used, and a standard uniform crossover operator was chosen.

The results are shown in Figure 21.2, where the relative distances to the best solution found by any of the algorithms are shown. As can be seen, the hybrid algorithm outperforms the original algorithms in most cases. Figure 21.3 shows the online evolution of the lower bound for the three algorithms in two instances. Notice how the hybrid algorithm yields consistently better results all over the run. This confirms the goodness of the hybrid model as an anytime algorithm.

Figure 21.2 Results of the B&B algorithm, the EA, and the first hybrid model for problem instances of different number of items (n), knapsacks (m), and the tightness ratio (α). Box plots show the relative distance to the best solution found by the three algorithms. In all box plots, the figure above indicates the number of runs (out of 10) leading to the best solution. A + sign indicates the mean of the distribution, whereas a marks its median. Boxes comprise the second and third quartiles of the distribution. Outliers are indicated by small circles in the plot.

Figure 21.3 Temporal evolution of the lower bound in the three algorithms for a problem instance with (a) α = 0.75, m = 30, n = 100, and (b) α = 0.75, m = 30, n = 250. Curves are averaged for the 10 runs in the case of the EA and the hybrid algorithm.

21.4.2 Results for the Second Model

We solved the same problems using the EA, a beam search (BS) algorithm (k_bw = 100), and the second hybrid algorithm. The upper bound was obtained solving the LP relaxation of the problem in all cases. A single execution for each instance was performed for the BS method, whereas 10 independent runs per instance were carried out for the EA and hybrid algorithms. The algorithms were run for 600 seconds in all cases. For the EA and hybrid algorithm, the size of the population was fixed at 100 individuals, initialized with random feasible solutions. With the aim of maintaining some diversity in the population, duplicated individuals were not allowed. The crossover probability was set at 0.9, binary tournament selection was used, and a standard uniform crossover operator was chosen. Execution results for the BS algorithm, the EA, and the hybrid model are shown in Figure 21.4. As can be seen, the hybrid algorithm provides better results for the largest problem instances regardless of the tightness ratio. For the smallest problem instances, the EA performs better. This may be due to the lower difficulty of the latter instances; the search overhead of switching from the EA to the B&B may not be worth while in this case. The hybrid algorithm only begins to be advantageous in larger instances, where the EA faces a more difficult optimization scenario. Notice also that the hybrid algorithm is always able to provide a solution better than or equal to the one provided by BS.

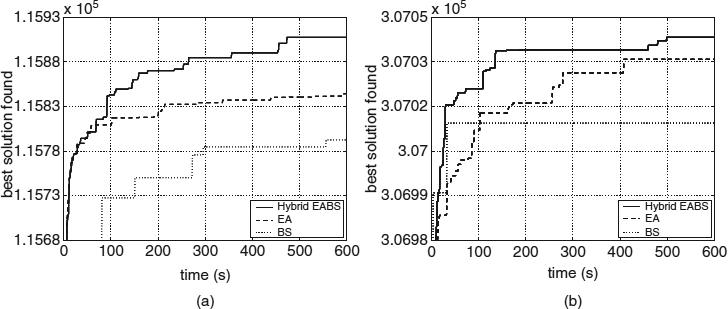
Figure 21.5 shows the evolution of the best value found by the various algorithms for two specific problem instances. Note that the hybrid algorithm always provides better results here than the original ones, especially in the case of the more constrained instance (α = 0.25).

Figure 21.4 Results of the BS algorithm, the EA, and the second hybrid model for problem instances of different number of items (n), knapsacks (m), and tightness ratio (α).

Figure 21.5 Evolution of the best solution in the evolutionary algorithm (EA), beam search, and the hybrid algorithm during 600 seconds of execution: (a) α = 0.25, m = 30, n = 500; (b) α = 0.75, m = 10, n = 500. In both cases, curves are averaged for 10 runs for the EA and the hybrid algorithm.

21.5 CONCLUSIONS

We have presented hybridizations of an EA with a B&B algorithm. The EA provides lower bounds that the B&B can use to purge the problem queue, whereas the B&B guides the EA to look into promising regions of the search space. The resulting hybrid algorithm has been tested on large instances of the MKP problem with encouraging results: The hybrid EA produces better results than the constituent algorithms at the same computational cost. This indicates the synergy of this combination, thus supporting the idea that this is a profitable approach to tackling difficult combinatorial problems.

Acknowledgments

The authors are partially supported by the Ministry of Science and Technology and FEDER under contract TIN2005-08818-C04-01 (the OPLINK project). The first and third authors are also supported under contract TIN2007-67134.

REFERENCES

1. E. L. Lawler and D. E. Wood. Branch and bounds methods: a survey. Operations Research, 4(4):669–719, 1966.

2. T. Bäck. Evolutionary Algorithms in Theory and Practice. Oxford University Press, New York, 1996.

3. T. Bäck, D. B. Fogel, and Z. Michalewicz. Handbook of Evolutionary Computation. Oxford University Press, New York, 1997.

4. A. E. Eiben and J. E. Smith. Introduction to Evolutionary Computation. Springer-Verlag, New York, 2003.

5. L. Davis. Handbook of Genetic Algorithms. Van Nostrand Reinhold, New York, 1991.

6. D. H. Wolpert and W. G. Macready. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1):67–82, 1997.

7. J. Culberson. On the futility of blind search: an algorithmic view of “no free lunch.” Evolutionary Computation, 6(2):109–128, 1998.

8. P. Moscato. Memetic algorithms: a short introduction. In D. Corne, M. Dorigo, and F. Glover, eds., New Ideas in Optimization, McGraw-Hill, Maidenhead, UK, 1999, pp. 219–234.

9. P. Moscato and C. Cotta. A gentle introduction to memetic algorithms. In F. Glover and G. Kochenberger, eds., Handbook of Metaheuristics. Kluwer Academic, Norwell, MA, 2003, pp. 105–144.

10. P. Moscato, A. Mendes, and C. Cotta. Memetic algorithms. In G. C. Onwubolu and B. V. Babu, eds., New Optimization Techniques in Engineering. Springer-Verlag, New York, 2004, pp. 53–85.

11. N. Krasnogor and J. Smith. A tutorial for competent memetic algorithms: model, taxonomy, and design issues. IEEE Transactions on Evolutionary Computation, 9(5):474–488, 2005.

12. A. H. Land and A. G. Doig. An automatic method for solving discrete programming problems. Econometrica, 28:497–520, 1960.

13. A. Barr and E. A. Feigenbaum. Handbook of Artificial Intelligence. Morgan Kaufmann, San Francisco, CA, 1981.

14. P. Wiston. Artificial Intelligence. Addison-Wesley, Reading MA, 1984.

15. G. L. Nemhauser and L. A. Wolsey. Integer and Combinatorial Optimization. Wiley, New York, 1988.

16. D. R. Anderson, D. J. Sweeney, and T. A. Williams. Introduction to Management Science: Quantitative Approaches to Decision Making. West Publishing, St. Paul, MN, 1997.

17. G. B. Dantzig. Maximization of a linear function of variables subject to linear inequalities. In T. C. Koopmans, ed., Activity Analysis of Production and Allocation. Wiley, New York, 1951, pp. 339–347.

18. N. Karmakar. A new polynomial-time algorithm for linear programming. Combinatorica, 4:373–395, 1984.

19. W. E. Hart and R. K. Belew. Optimizing an arbitrary function is hard for the genetic algorithm. In R. K. Belew and L. B. Booker, eds., Proceedings of the 4th International Conference on Genetic Algorithms, San Mateo CA. Morgan Kaufmann, San Francisco, CA, 1991, pp. 190–195.

20. W. E. Hart, N. Krasnogor, and J. E. Smith. Recent Advances in Memetic Algorithms, vol. 166 of Studies in Fuzziness and Soft Computing. Springer-Verlag, New York, 2005.

21. R. Dawkins. The Selfish Gene. Clarendon Press, Oxford, UK, 1976.

22. P. C. Chu and J. E. Beasley. A genetic algorithm for the multidimensional knapsack problem. Journal of Heuristics, 4:63–86, 1998.

23. P. Moscato and C. Cotta. Memetic algorithms. In T. F. Gonzalez, ed., Handbook of Approximation Algorithms and Metaheuristics. Chapman & Hall/CRC Press, Boca Raton, FL, 2007, Chap. 27.

24. Memetic Algorithms' home page. http://www.densis.fee.unicamp.br/~moscato/memetic_home.html, 2002.

25. H. Salkin and K. Mathur. Foundations of Integer Programming. North-Holland, Amsterdam, 1989.

26. O. H. Ibarra and C. E. Kim. Fast approximation for the knapsack and sum of subset problems. Journal of the ACM, 22(4):463–468, 1975.

27. B. Korte and R. Schrader. On the existence of fast approximation schemes. In O. L. Mangasarian, R. R. Meyer, and S. Robinson, eds., Nonlinear Programming 4. Academic Press, New York, 1981, pp. 415–437.

28. A. Caprara, H. Kellerer, U. Pferschy, and D. Pisinger. Approximation algorithms for knapsack problems with cardinality constraints. European Journal of Operational Research, 123:333–345, 2000.

29. D. Lichtenberger. An extended local branching framework and its application to the multidimensional knapsack problem. Diploma thesis, Institut für Computergrafik und Algorithmen, Technischen Universität Wien, 2005.

30. E. Balas and H. Martin. Pivot and complement: a heuristic for 0–1 programming. Management Science, 26(1):86–96, 1980.

31. C. Cotta and J. M. Troya. A hybrid genetic algorithm for the 0–1 multiple knapsack problem. In G. D. Smith, N. C. Steele, and R. F. Albrecht, eds., Artificial Neural Nets and Genetic Algorithms 3. Springer-Verlag, New York, 1998, pp. 251–255.

32. J. Gottlieb. Permutation-based evolutionary algorithms for multidimensional knapsack problems. In J. Carroll, E. Damiani, H. Haddad, and D. Oppenheim, eds., Proceedings of the ACM Symposium on Applied Computing, Villa Olmo, Como, Italy 2000. ACM Press, New York, 2000, pp. 408–414.

33. S. Khuri, T. Bäck, and J. Heitkötter. The zero/one multiple knapsack problem and genetic algorithms. In E. Deaton, D. Oppenheim, J. Urban, and H. Berghel, eds., Proceedings of the 1994 ACM Symposium on Applied Computation, Phoenix, AZ, ACM Press, New York, 1994, pp. 188–193.

34. G. R. Raidl. An improved genetic algorithm for the multiconstraint knapsack problem. In Proceedings of the 5th IEEE International Conference on Evolutionary Computation, Anchorage, AK, 1998, pp. 207–211.

35. G. R. Raidl and J. Gottlieb. Empirical analysis of locality, heritability and heuristic bias in evolutionary algorithms: a case study for the multidimensional knapsack problem. Technical Report TR 186–1–04–05. Institute of Computer Graphics and Algorithms, Vienna University of Technology, 2004.

36. H. Ishibuchi, S. Kaige, and K. Narukawa. Comparison between Lamarckian and Baldwinian repair on multiobjective 0/1 knapsack problems. In C. Coello Coello, A. Hernández Aguirre, and E. Zitzler, eds., Evolutionary Multi-criterion Optimization Proceedings of the 3rd International Conference on (EMO'05), Guanajuato, Mexico, vol. 3410 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2005, pp. 370–385.

37. I. Dumitrescu and T. Stutzle. Combinations of local search and exact algorithms. In G. L. Raidl et al., eds., Applications of Evolutionary Computation, vol. 2611 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2003, pp. 211–223.

38. S. Fernandes and H. Lourenço. Hybrid combining local search heuristics with exact algorithms. In F. Almeida et al., eds., Procedimiento V Congreso Español sobre Metaheurísticas, Algoritmos Evolutivos y Bioinspirados, Puerto de la Cruz, Tenerife, Spain, 2007, pp. 269–274.

39. J. Puchinger and G. R. Raidl. Combining metaheuristics and exact algorithms in combinatorial optimization: a survey and classification. In J. Mira and J. R. Álvarez, eds., Artificial Intelligence and Knowledge Engineering Applications: A Bioinspired Approach, Las Palmas, Canary Islands, Spain, vol. 3562 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2005, pp. 41–53.

40. M. Vasquez and J. K. Hao. A hybrid approach for the 0–1 multidimensional knapsack problem. In Proceedings of the International Joint Conference on Artificial Intelligence, Seattle, WA. Morgan Kaufmann, San Francisco, CA, 2001, pp. 328–333.

41. J. Denzinger and T. Offermann. On cooperation between evolutionary algorithms and other search paradigms. In Proceedings of the 6th IEEE International Conference on Evolutionary Computation, Washington, DC. IEEE Press, Piscataway, NJ, 1999, pp. 2317–2324.

42. C. Cotta and J. M. Troya. Embedding branch and bound within evolutionary algorithms. Applied Intelligence, 18(2):137–153, 2003.

43. C. Cotta, J. F. Aldana, A. J. Nebro, and J. M. Troya. Hybridizing genetic algorithms with branch and bound techniques for the resolution of the TSP. In D. W. Pearson, N. C. Steele, and R. F. Albrecht, eds., Artificial Neural Nets and Genetic Algorithms 2, Springer-Verlag, New York, 1995, pp. 277–280.

44. J. Puchinger, G. R. Raidl, and G. Koller. Solving a real-world glass cutting problem. In J. Gottlieb and G. R. Raidl, eds., Proceedings of the 4th European Conference on Evolutionary Computation in Combinatorial Optimization, Coimbra, Portugal, vol. 3004 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2004, pp. 165–176.

45. A. P. French, A. C. Robinson, and J. M. Wilson. Using a hybrid genetic-algorithm/branch and bound approach to solve feasibility and optimization integer programming problems. Journal of Heuristics, 7(6):551–564, 2001.

46. K. Kostikas and C. Fragakis. Genetic programming applied to mixed integer programming. In M. Keijzer, U. O'Reilly, S. M. Lucas, E. Costa, and T. Soule, eds., Proceedings of the 7th European Conference on Genetic Programming, Coimbra, Portugal, vol. 3003 of Lecture Notes in Computer Science. Springer-Verlag, New York, 2004, pp. 113–124.

47. A. Volgenant and R. Jonker. A branch and bound algorithm for the symmetric traveling salesman problem based on the 1-tree relaxation. European Journal of Operational Research, 9:83–88, 1982.

48. J. E. Gallardo, C. Cotta, and A. J. Fernández. Solving the multidimensional knapsack problem using an evolutionary algorithm hybridized with branch and bound. In J. Mira and J. R. Álvarez, eds., Proceedings of the 1st International Work-Conference on the Interplay Between Natural and Artificial Computation, Las Palmas, Canary Islands, Spain, vol. 3562 of Lecture Notes in Computer Science, Springer-Verlag, New York, 2005.

49. J. E. Gallardo, C. Cotta, and A. J. Fernández. A hybrid model of evolutionary algorithms and branch-and-bound for combinatorial optimization problems. In Proceedings of the 2005 Congress on Evolutionary Computation, Edinburgh, UK. IEEE Press, Piscataway, NJ, 2005, pp. 2248–2254.

50. J. E. Gallardo, C. Cotta, and A. J. Fernández. On the hybridization of memetic algorithms with branch-and-bound techniques. IEEE Transactions on Systems, Man and Cybernetics, Part B, 37(1):77–83, 2007.

51. J. E. Beasley. OR-library: distributing test problems by electronic mail. Journal of the Operational Research Society, 41(11):1069–1072, 1990.