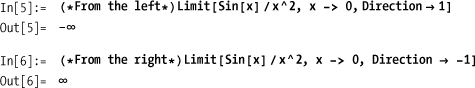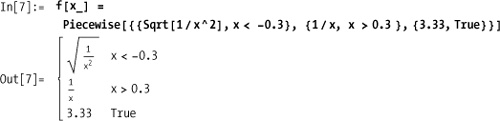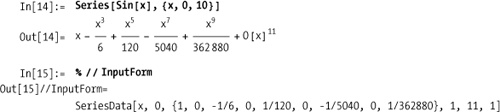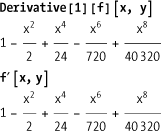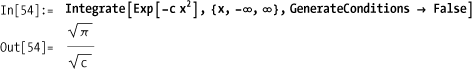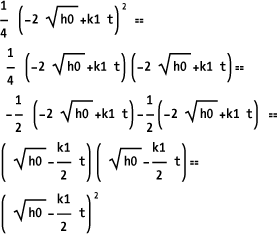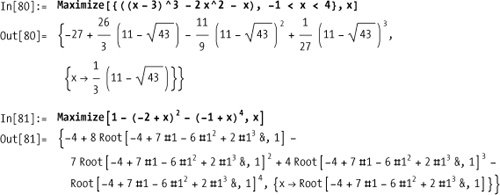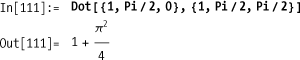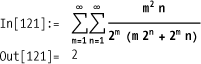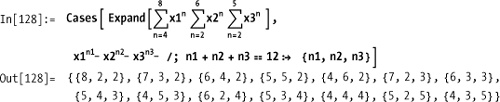A guide to all functions related to infinitesimal calculus can be found in the Mathematica documentation at guide/Calculus.

A guide to all functions related to discrete calculus can be found in the Mathematica documentation at guide/DiscreteCalculus.

You want to determine the value of a function as a variable approaches a specific value, even if evaluating the function at that limit may give an indeterminate result.

The functions Sin[x]/x, Sin[x^2]/x, and Sin[x]/x^2 each evaluate to the indeterminate value 0/0 at x = 0; however, their limits as x approaches zero are quite definite and different.

Plotting functions around the limiting value is often a good way to provide visual insight into the limiting value.

Here you can see that the last function has different limits depending on whether one approaches the limit from the left or the right. You can specify which limit you want using the option Direction.

You want to express a function in terms of two or more functions over different intervals.

Mathematica supports a function Piecewise for composing a complex function out of simpler functions using predicates to determine which of the simpler functions apply.

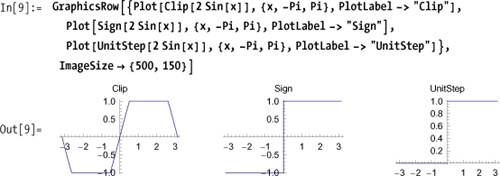
Clip, Sign, and UnitStep are special cases of built-in piecewise functions. Clip constrains its input to a minimum and maximum value (default -1 and +1). Sign gives -1 or 1 depending on whether the input is negative or positive, and UnitStep is 0 for negative values and 1 for values greater than or equal to zero.

You can differentiate and integrate piecewise functions, and you’ll get a piecewise function.

PiecewiseExpand can take a nested piecewise function and return a single function. You can use this to show that Min, Max, and Abs are also special cases of piecewise functions.

You want to find the series expansion of a function.

The Mathematica function Series will generate the series expansion of a function about a point to a specified order. It produces a SeriesObject, which Mathematica will display as a traditional series expansion.

You use Normal to create a regular Mathematica expression. Here I also use Evaluate because I am defining a function and want Normal to evaluate immediately even though the function is defined using SetDelayed (:=). Equivalently, you can use Set (=) to define the function without Evaluate.

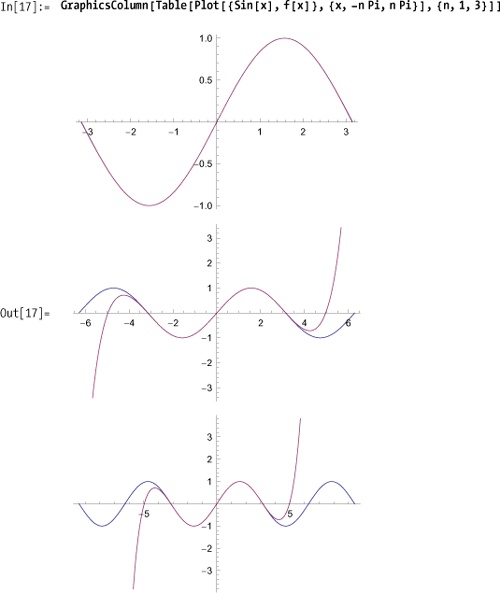
In[16]:= f[x_] := Evaluate[Normal[Series[Sin[x], {x, 0, 10}]]]

You visualize the accuracy of the series approximation by plotting over successively larger intervals. As expected, this series approximation begins to diverge as you move away from the origin.

You can compute the inverse of a series using InverseSeries.

You want to compute derivatives or partial derivatives of functions in symbolic form. You may do this as a means of creating new functions or as a means of teaching the concepts that underlie differentiation.

Mathematica allows you to enter derivatives in input form as D[f[x], x] or in standard form as ∂x f[x].

In[20]:= D[Sin[x],x]
Out[20]= Cos[x]

In[21]:= ∂xSin[x]       
Out[21]= Cos[x]

Higher-order derivatives are specified as D[f[x],{x,n}] where n is 2 for the second derivative, 3 for the third, and so on. In standard form, the second derivative can be entered as ∂{x,2} f[x].

In[22]:= D[Sin[x], {x, 2}]
Out[22]= -Sin[x]

Partial derivatives are easily accommodated as well using several equivalent notations.

In[23]:= D[Sin[x] Sin[y], {x, 1}]
Out[23]= Cos[x] Sin[y]

In[24]:= D[Sin[x] Sin[y], x, x, y]
Out[24]= -Cos[y] Sin[x]

In[25]:= D[Sin[x] Sin[y], {x, 2}, {y, 1}]
Out[25]= -Cos[y] Sin[x]

Mathematica also recognizes prime notation, but this notation is more commonly used in Mathematica when entering a differential equation. See the sidebar Mathematica’s Representation of Differentiation for some important subtleties.

In[26]:= {Sin'[x], Sin''[x]}
Out[26]= {Cos[x], -Sin[x]}

You can use D along with Solve to differentiate implicit functions. Simply use D as usual and use Solve to find the solution in terms of y'[x].

There are cases where you may want to use the D to synthesize a function on the fly. In this case, use Set (=) to perform the differentiation operation immediately or use Evaluate with SetDelayed (:=).

In[37]:= f1[x_] = D[Sin[Pi x Cos[x ^ 2]], x];

In[38]:= f2[x_] := Evaluate[D[Sin[Pi x Cos[x ^ 2]], x]]

In[39]:= {f1[2.], f2[2.]}

Out[39]= {-9.65614, -9.65614}

If you forget to do so, you will get an error when you call the function with a literal value.

Mathematica’s Representation of Differentiation

More importantly, the prime notation is not synonymous with D[] but rather with a differential operator of the form Derivative[n]. The operator form clarifies ambiguities that would result from using it with functions of more than one variable. Think of Derivative[n1, n2, ...] as an operator that acts on a function to produce the specific derivative. The number of n’s should not exceed the number of variables of the function since each n is associated with the nth derivative of the corresponding variable. Some examples should help clarify.

First derivative with respect to x:

First derivative with respect to x, then y:

Derivative[1,1][f][x,y]
f(1,1) [x,y] 

First derivative with respect to x, then second derivative with respect to y:

Derivative[1, 2][f][x, y]
f(1,2) [x,y]

For the most part, you should work with D[] directly, but keep the operator notation in the back of your mind because it is how Mathematica represents derivatives internally.

D[f[x, y], x, y] // FullForm
Derivative[1, 1][f][x, y]

Derivative[1, 1][f][x, y]
f(1,1)[x,y]

Many students will use Mathematica to check the answers to their calculus homework, but Mathematica is also useful for generating demonstrations of the fundamental concepts underlying differentiation. For example, the derivative of a function at a point is the slope of the tangent to the function at that point. Further, given two points, the slope of the secant drawn between these points approaches the derivative as the points approach each other along the curve. The following function uses Mathematica’s dynamic features to generate presentations of this fact using any function and starting points as input.

You want to solve problems that involve indefinite or definite integrals using symbolic integration.

Use Integrate or ∫ to compute single, double, or higher-order integrations. Indefinite integrals specify an expression and the variables of integration.

In[44]:= Integrate[1/x, x]
Out[44]= Log[x]

Definite integrals provide the minimum and maximum limits, which can be constants or expressions.

The minimum and maximum limits can be -Infinity or Infinity.

In[48]:= Integrate[1 /(x^3 + x^2), {x, 1, Infinity}]
Out[48]= 1 - Log[2]

Integrate will easily handle most integration problems you are likely to encounter in school, engineering, and science.

Double and higher-order integrals are computed with a single Integrate function by adding multiple integration variables. However, if you use the traditional integration notation, you will use multiple integral symbols.

Some integrations may return with conditionals and assumptions due to convergence issues. You can eliminate these by providing your own assumptions.

You also do this using GenerateConditions → False.

You can also get piecewise functions as a result of Integrate.

When Integrate is unable to solve the integration, it will return the unevaluated integral in symbolic form.

Applications of integration are numerous, and it would be impossible to provide even a small representative set of examples here. Rather, I will provide examples that emphasize how Integrate can be combined with other Mathematica functions in non-obvious ways.

A simple application is a function to compute the area between two arbitrary curves given two points. When you create functions that embed Integrate, you often want to allow options to pass through to increase generality.

This would generate a huge messy conditional if not for the ability to pass assumptions about the arbitrary bounds a and b.

Create a table of volumes of hyperspheres. Here Boole maps True to 1 and False to 0. Note that the list of integration limits must be converted to a sequence using Apply (@@). By the way, this is a very expensive way to calculate volume of a hypersphere, but it does illustrates how to parameterize the order of integration. Search for hyperspheres on Wikipedia or Wolfram’s MathWorld to find a more practical formula.

You can combine Integrate with differentiation to create a general function to compute the length of a curve between two points.

In[61]:= Clear[lengthOfCurve]

In[62]:= lengthOfCurve[expr_, var_, a_, b_, opts : OptionsPattern[]] :=
          Integrate[Sqrt[1 + D[expr, var] ^ 2], {var, a, b},
           Sequence @@ FilterRules[{opts}, Options[Integrate]]]

Or, you can compute the length of the hypotenuse of a right triangle.

Verify the formula for the circumference of a circle given its radius by taking twice the arc length of a semicircle.

Here is a purely symbolic solution with assumptions to simplify results.

You have a model of a system described by a differential equation and you want to solve that equation symbolically. Two related problems are getting the equation in a form Mathematica expects and getting the solution in the form you expect.

An undergraduate student of engineering or physics will commonly need to solve differential equations that model simple systems. A common problem is an undamped oscillator composed of a mass hanging from a spring. The problem may appear in a textbook as

In[66]:= m y'' + k y = 0

This says that the force (mass × acceleration) is balanced by the force of the spring, as given by Hooke’s law, where k is the spring constant. The key to solving this equation in Mathematica using DSolve is to make the equation more explicit. Specifically, the equation omits the time variable. You must also replace the = symbol with == and tell Mathematica what equation we are solving for and what are the variables.

The solution is given as a replacement rule, and since the equation is a second order, two constants, C[1] and C[2], are introduced. You can provide initial conditions to eliminate the constants. In this case, you can also render the solution in its customary form by replacing Sqrt[k]/Sqrt[m] by the angular frequency ω.

The solutions provided by DSolve are not automatically simplified, and you often will want to use Simplify or FullSimplify to postprocess them into a more mathematically friendly form. This is especially relevant when comparing the answer DSolve finds with answers provided in a typical textbook. Consider this problem adapted from Advanced Engineering Mathematics by Erwin Kreyszig (John Wiley). Here you want to find the solution to a differential equation describing the speed of a fluid flowing out of an opening in a container.

Given the physics of the problem, it should be clear we want the first solution (the second solution has the height increasing with time).

Although this has simplified the result somewhat, it is a much more complicated solution than the one provided by Kreyszig, which is

Did DSolve give the wrong result? A common mistake when using Mathematica is to prematurely substitute specific constants as I did above. It is often advisable to solve equations entirely in symbolic form and substitute constants later.

Although this did not get us all the way to the form of the book’s solution, you are more likely to see the final transformation that will demonstrate that DSolve was correct. It hinges on noticing that 1/4 is the same as (-1/2)*(-1/2).

Substituting h0 and kl with the constants shows that Mathematica did get the correct solution. Alternatively, you can ask Mathematica to prove its solution is equal to the book’s solution by using Resolve and ForAll. The only problem here is that Mathematica does not show its work!

You want to find the minimum or maximum values of a function. You may need to find these extremes subject to constraints or for numbers in a specific domain (e.g., integers).

Although there are standard techniques used in calculus for finding extrema, Mathematica provides the specific functions Minimize and Maximize, which provide a great deal of power.

For many applications of minimization or maximization, you are interested in the extreme value within a specific interval.

I restrict this discussion to Maximize for simplicity, but everything here applies to Minimize as well. If you are interested in displaying the result of Maximize, you will want to force the result to numerical form, as we did in the solution. Maximize will keep the result in exact form if it is given input in exact form. For polynomials, this typically means the result will be expressed in terms of radicals or Root objects. A Root[f,k] object represents the kth solution to a polynomial equation f[x] == 0.

Sometimes you want to find solutions for integer values only. You can constrain Maximize to the integers in one of two ways. You might recognize this problem as an instance of a knapsack problem where you are optimizing the value of the knapsack (item1 has value 8, item2 11, and so on) subject to size constraint of 14 where item1 has size 5 and so on.

A more convenient notation when all variables are integer is to specify the domain as the third argument to Maximize.

Maximize seeks a global maximum, whereas an alternative function, FindMaximum, seeks a local maximum (there is also FindMinimum for local minimums). FindMaximum allows you to specify a starting point for the search, but otherwise has a very similar form to Maximize. The following program demonstrates the difference between Maximize and FindMaximum. The advantage of FindMaximum is that it does not require the objective function to be differentiable.

You want to find solutions to problems within vector fields. Such problems arise in mechanics, electromagnetic theory, and fluid dynamics.

Simple vector calculus problems can be solved in terms of the calculus primitives discussed in this chapter’s recipes along with vector functions like Dot and Cross. For example, line integrals are commonly used to calculate work performed when moving a particle along a path in a vector field. Here F is the vector equation of the field, f is the equation of the path through the field, var is the parameter of f, and a and b are the start and end points of the path.

Another common operation in vector calculus is the surface integral over scalar functions and vector fields. Surface integrals are the 2D analog of line integrals. One way to think of the scalar surface integral is to imagine a surface f made of a material whose density varies as described by a second function g. The surface integral of f over g is then the mass per unit thickness.

In[93]:= surfacelntegralScalar[g_, f_, {v1_, v1a_, v1b_}, {v2_, v2a_, v2b_}] :=
          Integrate[g[f[v1, v2]] Norm[Cross[D[f[v1, v2], v1], D[f[v1, v2], v2]]],
           {v1, v1a, v1b}, {v2, v2a, v2b}]

For example, consider the surface fl, which is a half sphere over the interval { ϕ , 0, Pi/2} and { θ , 0, 2 Pi}, and compute the surface integral given a density function given by (x^2 + y^2) z.

If we use a constant function (uniform density), we get the surface area of the half sphere as expected (surface area of an entire sphere is 4 πr²).

In[97]:= g2[{x_, y_, z_}] := 1
         surfaceIntegralScalar[g2, f1, {ϕ, 0, Pi/2}, {θ, 0, 2 Pi}]
Out[98]= 2 π

For a vector field, there is a similar equation using Dot in place of scalar multiplication by the norm. The traditional way to visualize the vector surface interval is to consider a fluid flowing through a surface where there is a vector function F describing the velocity of the fluid at various points on the surface. The surface integral is then the flux, or the quantity of fluid flowing through the surface in unit time.

In[99]:= surfaceIntegralVector[F_, f_, {v1_, v1a_, v1b_}, {v2_, v2a_, v2b_}] :=
          Integrate[Dot[F[f[v1, v2]], Cross[D[f[v1, v2], v1], D[f[v1, v2], v2]]],
           {v1, v1a, v1b}, {v2, v2a, v2b}]

Here is the solution to the flux described by {3 y, -z, x^2} through a surface described parametrically as {s t, s + t, (s^2 - t^2)/2}.

In[100]:= f[s_, t_] := {s t, s + t, (s^2 - t^2) /2}
          F[{x_, y_, z_}] := {3 y, -z, x^2}
          surfaceIntegralVector[F, f, {s, 0, 1}, {t, 0, 3}]
Out[102]= -15

A standard result from electrostatics is that the net flux out of a unit sphere, for a field that is everywhere normal, is zero. We can verify this as follows:

In[103]:= F2[{x_, y_, z_}] := {1, 1, 1}/(x^2 + y^2 + z^2)

In[104]:= f2[θ_, ϕ_] := {Sin[ϕ] Cos[θ], Sin[ϕ] Sin[θ], Cos[ϕ]}

In[105]:= surfaceIntegralVector[F2, f2, {θ, 0, 2 Pi}, {ϕ, 0, Pi}]

Out[105]= 0

The solution shows how the calculus primitives and other Mathematica functions can be used to build up higher-order vector calculus solutions. However, if you are interested in solving problems in vector calculus, the package VectorAnalysis` is definitely worth a look. Be forewarned that you might be in for a bit of a learning curve with this particular package, but it offers a lot of functionality. An important feature of the package is that it simplifies working in different coordinate systems. Before you can make effective use of VectorAnalysis`, you need to understand how coordinate systems are used and which coordinate system is appropriate to your problem.

In[106]:= Needs["VectorAnalysis`"]

In[107]:= CoordinateSystem
Out[107]= Cartesian

In[108]:= SetCoordinates[Spherical]
Out[108]= Spherical[Rr, Ttheta, Pphi]

In[109]:= CoordinateSystem
Out[109]= Spherical

When you use VectorAnalysis`, you will typically want to use functions in that package in place of some standard Mathematica functions such as Dot and Cross. This is because the alternatives DotProduct and CrossProduct respect the current coordinate system. For example, if the current coordinate system is Spherical, you expect the following DotProduct to be zero because the vectors are orthogonal in spherical coordinates.

In[110]:= DotProduct[{1, Pi/2, 0}, {1, Pi/2, Pi/2}]
Out[110]= 0

In contrast, Dot and Cross always assume Cartesian coordinates.

Some of the most important vector calculus operations are Div (divergence), Grad (gradient), Curl, and the Laplacian. Although it would make a nice exercise to implement these from the calculus primitives, as I did for line and surface integrals, there is no need if you use the VectorAnalysis` package. These operations use the default coordinate system, or you can specify a specific coordinate system as a separate argument.

The divergence represents the instantaneous outflow of a vector field at each point.

The curl of a vector field represents the amount of rotation.

By definition, the divergence of the curl must be zero since the curl has no net outflow.

In[114]:= SetCoordinates[Cartesian[x, y, z]];
          Div[Curl[{1, 1, 1} / (x^2 + y^2 + z^2)]]
Out[115]= 0

The gradient of a function f is a vector-valued function that indicates the direction in which f is increasing most rapidly. If you were climbing a hill, you would move in the direction of the gradient at each point to reach the top (strictly speaking the gradient would only be guaranteed to be directing you to a local peak). You can visualize the meaning of the gradient by using VectorPlot. I restrict the result to 2D for easier visualization.

The Mathematica tutorial to the VectorAnalysis package is essential reading for using those functions.

Div, Grad, Curl, and All That by H. M. Schey (W.W. Norton) and Vector Calculus by Paul C. Matthews (Springer) are two of my favorite informal introductions to vector calculus.

You want to solve problems in discrete calculus that are expressed in terms of sums or products.

Mathematica can handle infinite sums and products with ease, provided, of course, they converge.

If sums or products don’t converge, Mathematica will let you know by emitting an error. You can test for convergence without evaluating the sum using SumConvergence.

As with Integrate, Sum can specify multiple summation variables. In traditional form these sums are rendered as a multiple summation, but keep in mind that these are entered as Sum[expr,{n,nmin,nmax},{m,mmin,mmaz}] rather than Sum[Sum[expr, {n,nmin,nmax}],{m,mmin,mmaz}].

This double summation has a surprisingly simply solution.

This is a very famous sum attributed to Srinivasa Ramanujan, one of India’s greatest mathematical geniuses. You might think that Mathematica is just doing some simple pattern matching to recognize this result; however, substitute for any of the magic constants in this formula, and Mathematica will handle it just as well (but don’t expect the answer to be as pretty).

Here is a very pretty formula for π that combines an infinite sum and an infinite product.

As of version 7, Mathematica can handle indefinite sums and products. Mathematica will seek to eliminate the sum if possible. For example, the sum over k of a polynomial is another polynomial that can be expressed in terms of k, and products over polynomials will invariably reduce to some expression involving Gamma.

The Z-transform is an important infinite sum used in signal processing. It is defined as Sum[f[n] z^-n,{n, 0, Infinity}], but is directly supported using ZTransform.

Here is an unconventional application for Sum, but one that is sometimes used in discrete math to introduce the idea of a generating function. You can use Sum to construct a generating function for solutions to problems like n1+n2+n3 == 12 subject to nl >= 4, n2 >= 2, and 5 >= n3 >= 2. Each Sum is constructed from the smallest number the associated variable can take to the largest, by considering the smallest the other variables can take. For example, xl must be at least 4 but can’t be greater than 12-2-2 = 8, since n2 and n3 must each be at least 2. Here we use Expand to generate the polynomial and Cases to find the exponents that sum to 12, thus giving all solutions.

If you only care about the number of solutions, it would fall out of the coefficient of x¹² in the expansion of this polynomial.

See 11.11 Generating Functions and Sequence Recognition for more information on generating functions in Mathematica.

Readers who are interested in gaining insight into the algorithms that underlie Mathematica’s amazing feats with infinite sums should read A=B by Marko Petkovsek, Herbert S. Wilf, and Doron Zeilberger (A K Peters), which is available online at http://bit.ly/1LJiwe .

You want to solve problems that arise in discrete systems such as finance, actuarial science, dynamical systems, and numerical analysis. Many such problems can be modeled as recurrence relations, also known as difference equations.

RSolve is used to solve difference equations. A simple problem where RSolve applies is in mortgage calculations. Suppose you want to derive a function for the outstanding principal over the life of a loan. Let’s say the yearly interest rate is 5.75%, the monthly payment is $1,000.00, and the term is 30 years. This loan can be described as the following difference equation. Here the constraint y[360] == 0 arises from the condition that the last payment is zero (I am using y[0] as the origin).

From this we can figure out the initial principal or the payoff at any given month:

In[133]:= y[0] /. sol[[1]]
Out[133]= 171358.

After 60 months, or 5 years, very little has been paid off, which is quite depressing but a fact of life.

In[134]:= y[0] - y[60] /. sol[[1]]
Out[134]= 12402.6

Setting up a difference equation is often a matter of solving the problem by hand for small values of n and then detecting the relationship between successive values. Consider the Towers of Hanoi puzzle. A one-disk problem is solved in one move (T[1] = 1), a two-disk problem is solved in three moves (T[2] = 3), and three-disk problem is solved in seven moves (T[3] = 7). It follows then that T[n] = 2 T[n-1] + 1.

A seemingly innocent difference equation can result in a solution involving complex numbers. This is a second-order equation, so two initial values are required to get an exact solution with no arbitrary constants.

Note that like DSolve, RSolve does not try to simplify the result. It is advisable to try to simplify it; in this case, you see that complex numbers disappear, and the result is in terms of trigonometric functions, which you may not have expected.

As with DSolve, if you do not provide initial conditions, you will get solutions involving arbitrary constants of the form C[N].

These solutions were found in terms of pure functions because we asked for the solution in terms of a, but you can change the form of the second argument to a[n] to get the solution in that form.

You can evaluate this solution for specific n and C[1] using ReplaceAll (//.).

One of the best introductions to the subject of difference equations is An Introduction to Difference Equations by Saber Elaydi (Springer).

You want Mathematica to generate a function associated with a particular sequence or to infer a function that will produce the sequence for successive integers.

Use FindGeneratingFunction to derive the generating function for a sequence. Recall that the power series of a generating function encodes the sequence in its coefficients.

Use FindSequenceFunction to find an expression that maps the integers to the specified sequence.

In[143]:= s = FindSequenceFunction[{1, 4, 9, 16, 25, 36, 49, 64, 81, 100}, n]
Out[143]= n2

In[144]:= Table[s, {n, 1, 12}]
Out[144]= {1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144}

FindSequenceFunction can deal with sequences that are not strictly increasing and with noninteger sequences.

You can synthesize a generating function from an expression using GeneratingFunction.

And recover the sequence to the Nth term using the following expression:

In[148]:= With[{N=12},
           1/Table[SeriesCoefficient[Simplify[Series[g, {x, 0, N}]], n], {n, 1, N}]]
Out[148]= {2, 6, 24, 120, 720, 5040, 40320, 362880,
           3628800, 39916800, 479001600, 6227020800}

For the nonexpert, a very approachable book on generating functions is Generatingfunctionology by Herbert S. Wilf (A K Peters). An online version can be found at http://bit.ly/3bkssK .