CHAPTER 2
WHAT IS A POLYHEDRON?
According to the Oxford English Dictionary, the first appearance of the term “polyhedron” in English was in Sir Henry Billingsley’s 1570 translation of Euclid’s (c. 300 BCE) Elements. “Polyhedron” comes from the Greek roots poly, meaning many, and hedra, meaning seat. A polyhedron has many seats on which it can be set down. Although the term hedra originally meant seat, it has been the standard term for the face of a polyhedron since at least Archimedes2. Thus a reasonable translation of polyhedron is “many faces.” By the time of Euler, the transliteration of hedra into Latin was well established.
Polyhedra are familiar three-dimensional geometric objects constructed from polygonal faces. Examples of polyhedra, shown in figure 2.1, include the common cube, the simple pyramid (known formally as the tetrahedron), the elegant icosahedron, and the soccer-ball-shaped truncated icosahedron.
Because of their beauty and symmetry, polyhedra have found a prominent place in art, architecture, jewelry, and games. Anyone who has walked by a store selling new-age items knows that some people believe polyhedra (crystals in particular) have mystical powers. Polyhedra appear in nature as well, taking the form of gemstones and single-celled organisms.
The properties of polyhedra have fascinated mathematicians for millennia. To prove theorems about polyhedra, it is crucial that we have a precise definition of the term. It was late in the development of the theory of polyhedra that anyone attempted to provide one. For many years mathematicians operated under the “you know one when you see one” definition of polyhedron. They adopted the philosophy of Humpty Dumpty, who said to Alice, “When I use a word, it means just what I choose it to mean—nothing more nor less.” That is never a good way to proceed. As Henri Poincaré (1854–1912) wrote:

Figure 2.1. Examples of polyhedra.
The objects occupying mathematicians were long ill defined; we thought we knew them because we represented them with the senses or the imagination; but we had of them only a rough image and not a precise concept upon which reasoning could take hold.3
Working without a proper definition can, and in this case did, generate theoretical inaccuracies and inconsistencies. As we will see, the rigor of Euler’s proof of his polyhedron formula suffered because he did not explicitly define “polyhedron”.
Agreeing on a suitable definition is surprisingly difficult. There have been many proposals over the centuries, not all of which are equivalent. Because of this inconsistency, there is no single definition of polyhedron that applies to the massive body of literature on these mathematical objects.
Naively we may define a polyhedron as a figure constructed from polygonal faces in which every edge is shared by exactly two faces, and from each vertex there emanates at least three edges. Indeed, this definition appears reasonable, but under close scrutiny we find that some such solids violate our intuitive sense of what a polyhedron should be. Whereas no one would disagree that the objects in figure 2.1 are polyhedra, we ask whether those in figure 2.2 (three of which satisfy our definition) should be so classified.
This is not a trick question. There is no historical consensus on whether the objects in figure 2.2 are polyhedra. The object on the far left, a cube with a corner removed, is a polyhedron according to most modern definitions; however the oldest definitions of polyhedron—those assumed implicitly by the Greeks and Euler, for instance—do not allow a polyhedron to have indentations. Likewise, the second shape satisfies many mathematicians’ criteria for being a polyhedron. But it has a tunnel running through it; it has the shape of a doughnut made from flat faces. Should we consider this a polyhedron? The third object consists of two polyhedra joined at a vertex, and the fourth is formed by joining two polyhedra along an edge. They are not, according to most definitions, polyhedra (although the third one does satisfy our criteria). Both figures have two interiors; if you were to fill them with water, you would have to fill two different compartments. And we could present other, even more pathological, examples that violate our sense of what a polyhedron should be.
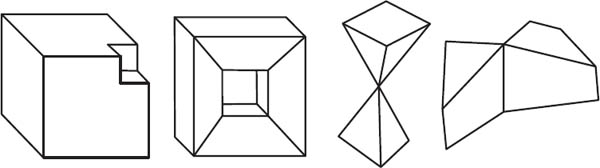
Figure 2.2. Shapes that are not convex polyhedra.
For now we take the easy way out and sidestep this thorny task of giving a rigorous definition. Because we will present the historical development of Euler’s formula, we can restrict our attention to a smaller class of polyhedra, one that is easier to define. We will take a very old-fashioned view of polyhedra, one with which Euler and the Greeks would agree. Although never stated explicitly, the historical assumption was that a polyhedron is convex. A convex polyhedron is an object that satisfies our naive definition (given above) and, in addition, has the property that any two points in the object can be joined by a straight line segment that is completely contained in the polyhedron. That is, a convex polyhedron cannot have any indentations. A quick inspection shows that every shape in figure 2.1 is convex and every shape in figure 2.2 is nonconvex.
We can see that this is what the Greeks assumed. They regarded the faces of a polyhedron as seats on which the polyhedron can rest. Every polyhedron of figure 2.1 can rest on any of its faces, but each polyhedron of figure 2.2 has at least one face that cannot be a seat of the polyhedron. Later, when we have more tools at our disposal, we will be able to apply Euler’s formula to a broader class of polyhedra; but for the benefit of simplicity, and for historical reasons, we now consider only convex polyhedra.
Before proceeding, let’s address one more historical discrepancy: is a polyhedron solid or is it hollow? Some definitions insist that polyhedra are solid, 3-dimensional objects, while others require that they be hollow, composed of a 2-dimensional “skin.” One who assumes the former definition would construct a polyhedron from clay, whereas someone adopting the latter would make a polyhedron out of paper. Early in the history of polyhedra, the assumption was that they were solid. In fact, for many centuries polyhedra were called “solids.” Later, as the theory of polyhedra made the transition to topology, the assumption of hollowness took hold. This assumption enabled theorems about polyhedra to be generalized to theorems about spheres and tori, which are, by definition, hollow. For most of what we have to say, either model will suffice. We will not make either assumption explicitly unless it is crucial to the discussion.
