CHAPTER 16
RUBBER SHEETS, HOLLOW DOUGHNUTS, AND CRAZY BOTTLES
By the middle of the nineteenth century mathematicians had a much better understanding of how Euler’s formula applied to polyhedra. It was during this time that they began to ask whether it applied to other objects. What if the figure was not a polyhedron made of flat faces, but instead was a curved surface like a sphere or a torus? If so, what must the partitions look like? Recall that in 1794 Legendre used a partition of a sphere by geodesic polygons to prove Euler’s formula, and Cayley showed that when we apply Euler’s formula to graphs, the edges need not be straight.
These discussions illustrate the ongoing transition from a geometric to a topological way of thinking about shapes. The popular press often uses the term “rubber-sheet geometry” to describe the field of topology to a public that is likely to be unfamiliar with the term. Although literal-minded mathematicians take exception to this extreme oversimplification, it is a reasonable way to describe the difference between topology and geometry. In geometry it is crucial that the objects of study be rigid. Measurements of angles and lengths, proofs of congruencies of figures, and computations of areas and volumes all rely on precise and unmoving geometric structure.
As we saw earlier, in some cases the rigid, unbending features of geometric figures are not needed, and worse, they often obscure the underlying mathematics. In Euler’s investigation of the bridges of Königsberg, he discovered that it was the general arrangement of features that was important, not their exact locations. This observation led to the creation of graph theory, one of the earliest incarnations of topology. Later we saw hints that the alternating sum V − E + F depended only on the general shape—the topology—of an object, and not on the number of faces or their configuration. We observed that for any sphere-shaped polyhedron, V − E + F = 2, for a polyhedron with g “tunnels,” V − E + F = 2 − 2g, and for any connected planar graph, V − E + F = 1.
So it is not difficult to imagine that Euler’s formula might apply to shapes other than polyhedra. Begin with a rubber polyhedron that satisfies V − E + F = 2. Can we alter this shape so that V − E + F ≠ 2? Not easily. If we were to inflate it like a balloon so that all the faces and edges became curved, the alternating sum would not change. If we were to squeeze it, twist it, or pull it, the relationships among the numbers of vertices, edges, and faces would remain the same. Only by using a knife to cut a gash in the side of the baloon would the alternating sum change (it would create at least one new edge). In the next chapter we will discuss in more detail what it means for two shapes to be topologically “the same,” and we will investigate how Euler’s formula applies to various topological shapes.
The mathematical term “topology” dates back to 1847 (it had a botanical meaning earlier than that). It first appeared in German in the title of Listing’s book Vorstudien zur Topologie,1 although he had already been using the term in correspondence for ten years. The first appearance in English was in Peter Guthrie Tait’s (1831–1901) eulogy of Listing in 1883. He wrote, “The term Topology was introduced by Listing to distinguish what may be called qualitative geometry from the ordinary geometry in which quantitative relations chiefly are treated.”2
The term “topology” did not catch on immediately. Influential mathematicians such as Henri Poincaré and Oswald Veblen continued to use the French term analysis situs. The great early-twentieth-century topologist Solomon Lefschetz (1884–1972) was not so enamored with this term. He referred to analysis situsas “a beautiful but awkward term.”3
Lefschetz’s route to greatness was a curious one. He was born to Turkish parents in Russia in 1884, was raised and schooled in France, emigrated to America, and took a job as an engineer in Philadelphia. At the age of twenty-six, not long after losing his hands and forearms in a work-related accident, he decided to pursue a career in mathematics. He completed his PhD at Clark University in a single year, and taught briefly in Nebraska before taking a position at the University of Kansas at Lawrence. Then, at forty, after more than a decade of important work, he was hired by Princeton University. He received numerous honors in his long and distinguished career, including the National Medal of Science.

Figure 16.1. Ants on the surface of a sphere and a torus.
According to Albert Tucker (1905–1995), one of Lefschetz’s students, it was Lefschetz who popularized the use of the term “topology.” He titled his influential 1930 book for the American Mathematical Society Topology. According to Tucker:
Lefschetz wanted a distinctive title and also, as he would say, a snappy title, so he decided to borrow the word Topologie from German. This was odd for Lefschetz since he was French trained and analysis situs was Poincaré’s term; but once he decided on it, he conducted a campaign to get everyone to use it. His campaign succeeded quickly, mainly I think because of the derivative words: topologist, topologize, topological. That doesn’t go so well with analysis situs!4
We begin our investigation of topology by looking at surfaces. Examples of surfaces are a 2-dimensional plane, a sphere, a torus, a disk, and a cylinder. A surface is any object that looks locally like a plane. If an ant were to sit on a large surface, it would think that it was sitting on a 2-dimensional expanse. This is not out of our realm of experience—the earth is a spherical globe, but it is so large that to its inhabitants it is indistinguishable from a flat plane. A clever ant may be able to discover that its surface is not flat by venturing out and exploring the surface (just as Columbus tried to do when he sailed west toward “the Indies”), but standing still, it would have no idea.
It is important to be aware of the difference between intrinsic and extrinsic dimension. As the ant on a surface will tell you, it is locally 2-dimensional—the intrinsic dimension of a surface is two. However, for us to build a physical copy of this surface, the surface must live somewhere, and the dimension of this enveloping space is the extrinsic dimension. The sphere and the torus have an intrinsic dimension of two, but they must live in 3-dimensional space, so their extrinsic dimension is three. Shortly we will encounter bizarre surfaces that cannot be constructed in 3-dimensional space. Their extrinsic dimension is four. From a topological point of view, the intrinsic dimension of a surface is the most important; that is why we say that surfaces are 2-dimensional.
Surfaces are characterized by local simplicity and global complexity. In other words, up close, they are all identical. They all look like the Euclidean plane. However, globally they can differ substantially. They can loop back upon themselves, they can have holes, they can be twisted or knotted, and so forth.
A sphere and a torus are examples of closed surfaces. They have no punctures, they do not run off to infinity, and they do not have any sharp boundaries. Sometimes we want to consider surfaces that are not closed. A disk and a cylinder are examples of surfaces with boundary. A surface with boundary is still locally 2-dimensional, except that it may have one or more 1-dimensional boundary curves. Some flat-earthers believed that the earth had a boundary. On such a planet the unlucky Columbus would not reach the Indies, but would instead sail off the edge of the ocean.
For simplicity, when we use the term “surface,” we will mean compact surface. “Compact” is a technical term that means the surface is bounded and contains all of its boundary curves. In other words, we will not consider unbounded surfaces such as the 2-dimensional plane or a piece of cylindrical tubing that runs infinitely far in both directions. When we say that the surface must contain all of its boundary curves, we mean to exclude surfaces such as the open unit disk (x2 + y2 < 1). The open unit disk is the set of all points strictly less than one unit away from the origin; it is the unit disk (x2 + y2 ≤ 1) with the boundary circle removed. A good analogy is the frayed pant legs after the cuffs are removed—we need those cuffs.
In 1882 Felix Klein (1849–1925) devised an ingenious way of constructing surfaces.5 He began with a polygon (imagine that it is made of a very pliable rubber material). He created a surface by gluing sides of the polygon together in pairs. For example, if we begin with a square, roll it up, and glue together the two opposite sides, we obtain a cylinder (see figure 16.2). Notice that if instead of rolling the square into a cylinder, we were to keep the entire figure in the plane and distort it until the opposite edges meet (we need it to be made of a very soft rubber!), it would form a washer-shaped annulus. To a topologist a cylinder and an annulus are indistinguishable.

Figure 16.2. A cy inder or annulus.

Figure 16.3. Making a torus from a square.
To make it clear which sides will be glued and with which orientation, it is common to decorate them with arrows. There are two different ways to glue together a pair of sides—with or without a twist. So we use the arrows to show the proper alignment. When we need to glue together more than one pair of sides, we use different numbers of arrows or arrows of different shapes to indicate which pairs attach to which. In figure 16.3 we glue both pairs of opposite sides of a square together. We illustrate this by putting a single arrow on one pair of sides and double arrows on the other pair. First we glue one pair of sides to obtain a cylinder. Then, since the two end circles have compatible orientations, we join these together to obtain a torus.
Some old arcade-style video games, such as Asteroids, employed this representation of a torus. When the space ship flew off the side of the rectangular screen, it would suddenly reappear on the opposite side (see figure 16.4). If it flew off the top of screen, it would rise from the bottom. Other games had other topological configurations. Pac-Man, for instance, was played on a cylinder.

Figure 16.4. Arcade games played on a torus and a cylinder.

Figure 16.5. A double torus.
We do not have to confine ourselves to squares when constructing surfaces. In figure 16.5 we see an octagon with four different pairs of sides identified (they are given by single and double arrows, and one and two triangles). To see the shape of the resulting surface, it helps to make an additional cut diagonally through the octagon (we put three arrows on the cuts so that we will be able to glue them back together later). We deform these two pentagons into two squares, each with an indentation. These squares resemble the square in figure 16.3, so after they are glued they each form a torus with a hole in it. Finally, we glue the two tori together along the holes and we obtain a two-holed torus (or double torus).
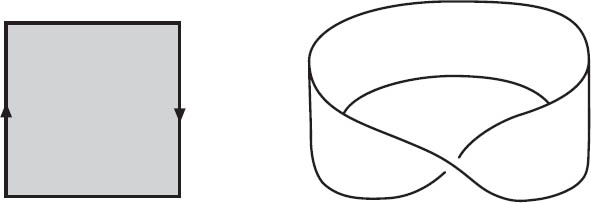
Figure 16.6. A Möbius band.
Klein proved that any surface can be represented as a polygon with sides glued together in pairs, but there may be many polygonal representations of the same surface. Fortunately, each surface has a “nice” polygonal representation such as our examples, and by cutting and regluing, any polygonal representation can be transformed into the nice one.6
In each of the examples we have seen thus far, the sides of the polygons have been glued without any twisting. In figure 16.6 we have a square in which a pair of opposite sides are glued together with a twist. Because the square is made of rubber, we can stretch it out, roll it up as if we are making a cylinder, and apply a half-twist before gluing. This shape is the well-known Möbius band or Möbius strip.
Although the construction of the Möbius band is simple, it has many surprising properties. Unlike the cylinder, the Möbius band has only one side. An ant walking along the centerline of a Möbius band would eventually return to the same location, but would be standing on the other side. Said another way, we can paint a cylinder red on one side and blue on the other, but a Möbius band must be all red or all blue. Also unlike the cylinder, the Möbius band has only one boundary. The ant sees an edge to the left and an edge to the right, but little does it know that they are both the same edge.
The Möbius band is a favorite topological entity for mathematics enthusiasts. It has been reproduced by many sculptors and artists. The most famous artistic rendering is probably M. C. Escher’s (1898–1972) 1963 woodcut featuring (what else!) ants crawling on a Möbius band (figure 16.7). It has appeared in literature—usually science fiction—such as Arthur C. Clarke’s 1949 short story “The Wall of Darkness.”7 It formed the basis for Gary Anderson’s award-winning design in the 1970 Earth Day contest to create the now-ubiquitous recycling symbol.* It has been used to create conveyor belts and tape loops so that they wear evenly.

Figure 16.7. Two famous Möbius bands: M. C. Escher’s Möbius Strip II(1963) and the recycling symbol.
The Möbius band is even the basis of a magic trick with the mysterious name of “Afghan bands” that dates back to at least 1882. A circus magician holds up three loops of fabric, which he explains are cloth belts. The problem, he laments, is that he needs belts for two clowns, the fat lady, and the Siamese twins. He takes the first band, rips it down the centerline and produces the belts for the two clowns. He rips the second band in the same way, but instead of two loops, he holds a single loop that has twice the circumference of the original—the belt for the fat lady. Finally, to get the belts for the twins, he rips the third loop and obtains two belts that are linked together. The trick, as we see in figure 16.8, is that the loops have twists in them (zero, one, and two half-twists, respectively). For maximum effect, the fabric or paper should be flexible and be much narrower than it is long so that the audience does not notice the twisting. Stephen Barr suggests the following dramatic alteration.8 Before the show, secretly apply a flammable liquid to the centerline of a twisted loop. In the presence of the audience, tack the edge of the loop to the wall and hold a match to the fabric. After a burst of flame, the loop falls apart into the desired configuration.
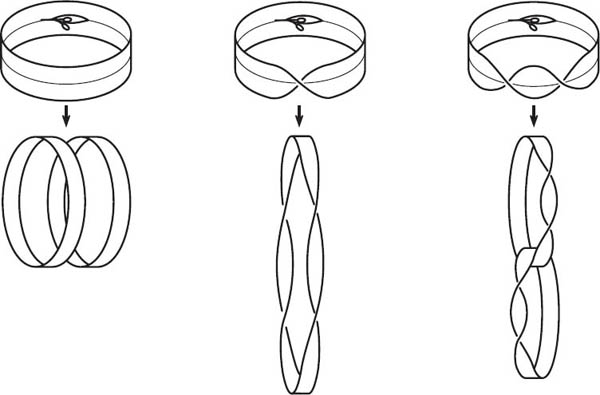
Figure 16.8. Afghan bands.
The reader is encouraged to set the book aside to try these cutting tricks and other variations (see appendix A for templates). Try giving the bands more than two half-twists. Try cutting a Möbius band along the line 1/3 of the way between the “two” boundaries. The author’s personal favorite is a trick due to Stanley Collins.9 Pass the band through a wedding ring before giving three half-twists and gluing into a band. When this band is cut down the middle it will have a knot in it, and inside the knot is the wedding ring!
The Möbius band is named after Möbius, but it was discovered almost simultaneously by Listing (it was Listing who first observed the mathematics behind what would become the Afghan bands trick). Listing published his description of the Möbius band in 1861,10 four years earlier than Möbius did.11 Their correspondences and notes show that the first appearance was in Listing’s hand (in July 1858), beating Möbius (September) by a few months.
The reason the Möbius band is not called the Listing band is that Möbius was the first to make mathematical sense of the one-sidedness property of the band. Today we call such surfaces nonorientable. There are several ways of describing this phenomenon mathematically. Möbius showed that it is impossible to divide the Möbius band into triangles, then orient the triangles so they match up with their neighbors (see figure 16.9).

Figure 16.9. A traingulation of a Möbius band cannot be oriented.

Figure 16.10. The Möbius band is not orientable.
Later Klein defined orientability in a different way. Place a small circle on the surface and pick an orientation. This circle is not drawn on one side of the surface, but is part of the surface so it is visible on both sides (on one side it is oriented clockwise, and on the other it is oriented counterclockwise). Imagine that the surface is made of tissue paper and the circle is drawn with a felt-tipped marker which bleeds through to the other side. Klein called such an oriented circle an indicatrix. If it is possible to slide this indicatrix around the surface in a such a way that when it returns to its original location, the orientation is opposite, then the surface is nonorientable. In figure 16.10 we show that the Möbius band is nonorientable by sliding the indicatrix around the center circle.
Walther von Dyck (1856–1934), a student of Klein, gave yet another definition. He put a movable coordinate frame, an x- and y-axis, on the surface. If it is possible to move the coordinate frame around the surface in such a way that the axes switch places, then the surface is nonorientable. (One benefit of Dyck’s approach is that it easily generalizes to higher-dimensional topological objects.)
It is interesting to note that mathematicians do not use the one-sidedness property to define nonorientability. Although one-sidedness may seem to be equivalent to nonorientability, Klein and Dyck argued that one-sidedness loses all meaning in higher dimensional spaces, but nonorientability does not. Sides only make sense for surfaces living in 3-dimensional space. It is meaningless to refer to the inside or outside of a surface—even a sphere—in 4-dimensional space.

Figure 16.11. A curve in the plane is two sided, but one in 3-dimensional space has no sides.
This and other assertions we will make about high-dimensional spaces are difficult to grasp. They require mental gymnastics that human beings are not hard wired to perform. As the mathematician Thomas Banchoff wrote, “All of us are slaves to the prejudices of our own dimension.”12
To illustrate the perplexing claim that surfaces in 4-dimensional space have no sides, we drop down a dimension from surfaces to curves. As we see in the left-hand image of figure 16.11, for a given point on a planar curve, normal vectors can point in only two possible directions (a vector is normal to a curve if it is perpendicular to the line tangent to the curve). So a planar curve has sides, and because it is impossible to move a normal vector around the curve so that it returns pointing in the opposite direction, it is two-sided. If the curve happens to be a simple closed curve—a closed loop that does not cross itself—then we call these directions the inside and the outside (actually, the seemingly obvious statement that every simple closed curve has an inside and an outside is a deep theorem known as the Jordan curve theorem).
On the other hand, for a curve in 3-dimensional space, there are infinitely many normal directions at each point (as illustrated by the disk of normal vectors in the right-hand image in figure 16.11). So in this case the term “sides” has no meaning.
Similarly, at any point on a surface in 3-dimensional space, there are two normal directions (a normal vector is perpendicular to the plane tangent to the surface). For nonorientable surfaces it is possible to move a normal vector around the surface so that it comes back pointing in the opposite direction, so it is one-sided (see figure 16.12). For orientable surfaces, this is not possible, so they are two-sided. But for a surface in 4-dimensional space, there are infinitely many normal directions at a point, so, as for a curve in 3-dimensional space, “sides” is meaningless.

Figure 16.12. In 3-dimensional space the Möbius band is one-sided and the torus is two-sided.

Figure 16.13. A Klein bottle.
The Möbius band is not the only nonorientable surface. In 1882 Klein discovered another, this one having no boundary, and it now bears the name the Klein bottle.13 In figure 16.13 we depict it in terms of a square with sides glued. We must glue opposite sides together; the left and right pair is glued with a twist and the top and bottom pair without. To construct the Klein bottle, glue together the two similarly oriented sides to obtain a cylinder. If we were to wrap this cylinder around like a torus, we would find that the ends have opposite orientations. Instead, the cylinder must “pass through” itself and come in from behind so that the end circles line up with the same orientations.
Figure 16.14. With a slight detour in the third dimension, we can allow two lines to pass without crossing.
What do we mean by “pass through”? We do not mean it literally. The Klein bottle is our first example of a surface that cannot be constructed in 3-dimensional space. When we say that the bottle passes through itself, it actually passes by itself in the fourth dimension. To illustrate this baffling concept, we again drop down a dimension. Suppose we wanted to draw two nonparallel lines in the plane that have no point of intersection. Clearly this is impossible, but if we were able to leave the 2-dimensional paper and use the third dimension, then, just before getting to the point of intersection, we could hop over the line (see figure 16.14). Thus, the two lines are essentially planar, but would need a small amount of the third dimension. Using this same technique we can construct the Klein bottle. When it comes to passing the tube through itself, it should make a small hop over itself in the fourth dimension.
Let us return to the square to create one final surface. This last one is the most difficult to visualize. It is formed by gluing together the opposite sides, but both with a twist (figure 16.15). Begin by taking the square piece of rubber and deforming it so that it takes the shape of a bowl. We are careful to keep track of which segments of the boundary should be glued to which other segments. Continue to deform this bowl so that the sides that need to be glued are aligned next to each other with the same orientation. Glue one pair of sides together (in figure 16.15 we glued the sides marked with double arrows). As we can see, we are in a bit of trouble—this gluing forced the remaining pair of sides to be on opposite sides of the new surface. In order to make the final gluing we must make use of the fourth dimension to allow the surface to pass by itself. In figure 16.15 we give two different views of this bizarre nonorientable surface called the projective plane.
The projective plane did not first appear in this context—as an object created by the gluing of surfaces. Instead, as the name suggests, it was an object studied in projective geometry, a geometric system in which any two lines, even those that are parallel, meet at a single point. Klein and Ludwig Schläfli (1814–1895) were the first to recognize that the projective plane was nonorientable.
Figure 16.15. The projective plane.
Appendix A contains templates for making the cylinder, the torus, the Möbius band, the Klein bottle, and the projective plane out of paper.
Klein gave one method of creating complicated surfaces from simpler shapes—gluing the sides of polygons together in pairs. We now present another way of constructing complicated surfaces from simpler ones. We start with a sphere and glue onto it cylindrical handles to make orientable surfaces and Möbius bands to make nonorientable surfaces.
As we see in figure 16.16, to add a handle to a surface, cut out two disks and glue the ends of a cylinder to the boundaries of the holes. A sphere with one handle is a torus. We build a double torus by adding another handle, and a g-holed torus by adding g handles to a sphere.
The number of handles on such a surface is intimately related to a topological quantity called the genus. The genus of an orientable surface (with or without boundary) is the maximum number of nonintersecting closed curves along which we can cut so that the surface is not disconnected.
To illustrate this concept, consider a sphere. Cutting along any simple closed curve will disconnect the sphere. This is another application of the Jordan curve theorem just as in the plane, a simple closed curve will divide the sphere into two regions. So the genus is O. On the other hand, it is possible to cut a loop on the surface of a torus so that it remains connected (see figure 16.17), but after this first cut, it is impossible to find another such closed curve. So the genus of a torus is 1.

Figure 16.16. A sphere with a handle (a torus).

Figure 16.17. Surfaces of genus 1, 2, and 3.
The genus of a sphere with handles is simply the number of handles. A double torus has genus 2 and in general, a g-holed torus has genus g. The genus of a surface gives a rigorous way of defining Lhuilier’s count of the number of “tunnels.” We could define the genus for nonorientable surfaces, and some people do. However, because the genus is so intimately related to the number of holes of a torus, it is not usually used in the nonorientable case.
Just as we can create an array of orientable surfaces by adding handles, we can use a similar procedure to create nonorientable surfaces. In order to understand this procedure, we must return to the Möbius band. One of its notable properties is its single boundary circle. The Möbius band is usually drawn so that this circle wraps around the twisted cylinder two times. Our aim is to manipulate the Möbius band so that its boundary circle appears like a regular circle, not one twisted twice. Clearly we need four dimensions to accomplish this feat of topological yoga.

Figure 16.18. A Möbius band is the same as a cross cap.
In figure 16.18 we see the Möbius band deformed in this way. Notice that this figure passes through itself along an entire line segment. The self-intersection at the top of this Möbius band with the cusp at the top and the crisscrossing surface below it is often called a Whitney umbrella, named for the topologist Hassler Whitney. This strange presentation of the Möbius band is called a cross cap. The resemblance to a projective plane should be apparent, because a cross cap is simply a projective plane with a disk removed.
We can form nonorientable surfaces by attaching Möbius bands. To do so, remove a disk from the surface and glue the circular boundary of a Möbius band to the boundary of the hole. As we can see in figure 16.19, it is easier to visualize the gluing by replacing the typical Möbius band by a cross cap. We create a projective plane by adding one cross cap to a sphere. Stated another way, a projective plane is a Möbius band with a disk glued to its boundary.
It is not as easy to see, but a sphere with two cross caps is a Klein bottle. Equivalently, a Klein bottle is obtained by gluing two Möbius bands together along their boundaries. Thus, the limerick at the beginning of the chapter makes sense. Gluing more than two cross caps to a sphere yields even stranger nonorientable surfaces.
Figure 16.19. A sphere with a cross cap (creating a projective plane).
We now have two ways to construct orientable and nonorientable surfaces. In the next chapter we will investigate how to apply Euler’s formula to these surfaces. We will also present the classification theorem for surfaces that states that every closed surface can be made by adding handles and cross caps to a sphere.
* Actually, at some point a variation of Anderson’s recycling symbol having three half-twists sprung up. Now it is common to encounter both versions.



