CHAPTER 7
EULER’S GEM
On November 14, 1750, the newspaper headlines should have read “Mathematician discovers edge of polyhedron!”
On that day Euler wrote from Berlin to his friend Christian Goldbach in St. Petersburg. In a phrase seemingly devoid of interesting mathematics, Euler described “the junctures where two faces come together along their sides, which, for lack of an accepted term, I call ‘edges.’ ”2 In reality, this empty-sounding definition was the first important stone laid in the foundation that would become a grand theory.
One of Euler’s great gifts was his ability to consolidate isolated mathematical results and create a theoretical framework into which everything fits. In 1750 he set out to do this with polyhedra. He began what he hoped would be a study of the foundations of polyhedra, or stereometry, as he called it.
By then the theory of polyhedra was over two thousand years old, but it was purely geometric. Mathematicians focused exclusively on metric properties of polyhedra—properties that could be measured. They were interested in finding lengths of sides and diagonals; computing areas of faces; measuring plane angles; and determining volumes.
Euler’s fist step was not in this metric tradition. He hoped to discover a way to group together, or classify, all polyhedra by counting their features. After all, this is how we classify polygons—all three sided polygons are triangles, four-sided ones are quadrilaterals, and so on.
The difficulty of classifying polyhedra in this way is quickly apparent. The obvious feature to count—the number of faces—is not sufficient to distinguish a polyhedron. As we see in figure 7.1, polyhedra having the same number of faces can be quite different.
Euler’s first brilliant insight was that the surface of a polyhedron is composed of 0-, 1-, and 2-dimensional components, namely vertices (or solid angles, as he called them), edges, and faces, and that these were the features we must count. These three quantities became the standard building blocks of all topological surfaces. He wrote:

Figure 7.1. Three different eight-sided polyhedra.
Therefore three kinds of bounds are to be considered in any solid body; namely 1) points, 2) lines, and 3) surfaces, or, with the names specially used for this purpose: 1) solid angles, 2) edges, and 3) faces. These three kinds of bounds completely determine the solid.3
We cannot overstate the importance of this realization. Amazingly, until he gave them a name, no one had explicitly referred to the edges of a polyhedron. Euler, writing in Latin, used the word acies to mean edge. In “everyday Latin” acies is used for the sharp edge of a weapon, a beam of light, or an army lined up for battle. Giving a name to this obvious feature may seem to be a trivial point, but it is not. It was a crucial recognition that the 1-dimensional edge of a polyhedron is an essential concept.
For the faces of a polyhedron Euler used the well-established term hedra, which, as we have already mentioned, translates as “face” or “base.” Euler referred to a vertex of a polyhedron as an angulus solidus, or solid angle. Before Euler wrote about polyhedra, solid angles were 3-dimensional entities defined by the faces that met at a point. A solid angle of a cube is different from a solid angle of a tetrahedron; they are distinguished by the geometry of the region they enclose. By the description given above—in which Euler associated a solid angle with a point—we see that he viewed the solid angles as zero-dimensional. When he said solid angle, he meant the very tip of the solid angle, not the 3-dimensional region that the faces enclose. The distinction is subtle, but the recognition that solid angles can be viewed as single points was crucial for his theorem. Nonetheless, Euler missed an opportunity by not giving them a new name. The vertex of a polyhedron is different from the solid angle on which it sits. In 1794 Adrien-Marie Legendre (1752–1833) made this point precisely:

Figure 7.2. An East German stamp featuring Euler and his formula.
We often use the word angle, in common discourse, to designate the point situated at its vertex; this expression is faulty. It would be more clear and more exact to denote by a particular name, as that of vertices, the points situated at the vertices of the angles of a polygon, or of a polyhedron. In this sense is to be understood the expression vertices of a polyedron [sic], which we have used.4
Once the great Euler honed in on these three key features—vertices, edges, and faces—and started tallying their numbers for various families of polyhedra, he probably saw the relationship quickly. We can imagine Euler’s surprise when he discovered that for any polyhedron, they satisfy the relationship
V − E + F = 2.
It is no wonder he expressed shock that no one had noticed it before. Brilliant Greek and Renaissance mathematicians had devoted countless hours to examining every conceivable aspect of polyhedra. How did they miss this elementary relationship?
The easy answer is the flippant retort that the history of mathematics is riddled with obvious theorems that went unnoticed for years. A more penetrating answer, however, is that the mathematicians who preceded him never viewed polyhedra in this way. Euler’s predecessors were so focused on metric properties that they missed this fundamental interdependence. Not only did it not occur to them that they should count the features on a polyhedron, they did not even know which features to count.
Euler is indeed the master of us all.
Euler’s work on the polyhedron formula was marked by three important documents. The first was his announcement to Goldbach in 1750 of his discovery of this relationship. He wrote:
In every solid enclosed by plane faces the sum of the number of faces and the number of solid angles exceeds by two the number of edges, or H + S = A + 2.5
Euler used the letters H, A, and S to denote the number of faces (hedra), edges (acies), and vertices (anguli solidi). Renaming these quantities and rearranging the terms yields the familiar relationship:
EULER’S POLYHEDRON FORMULA
A polyhedron with V vertices, E edges, and F faces satisfies V − E + F = 2.
In this letter Euler also included, without proof, ten other observations about polyhedra. He ended the letter by singling out the polyhedron formula and one other (which we will discuss in chapter 20) as the most important. Disappointed, he conceded that these two formulas “are so difficult that I have not yet been able to prove them in a satisfactory way.”6
In 1750 and 1751 Euler wrote two papers about his polyhedron formula. Because of the slow turnaround of journal articles, they did not appear in print until 1758. In the first paper, “Elementa doctrinae solidorum” (“Elements of the doctrine of solids”),7 he began his study of stereometry. For the first thirty pages, Euler made general remarks about polyhedra. Then Euler began his discussion of the relationship among the numbers of vertices, edges, and faces. He proved several theorems that relate V, E, and F and verified that V − E + F = 2 holds in several special cases. But he did not give a proof that the formula holds for all polyhedra. Still stymied and unable to complete the proof, he wrote, “I have not been able to find a firm proof of this theorem.”8
The following year he published a second paper, “Demonstratio nonnullarum insignium proprietatum quibus solida hedris planis inclusa sunt praedita” (“Proof of some notable properties with which solids enclosed by plane faces are endowed”).9 Here he was finally able to give a proof of his polyhedron formula. Despite the fact that Euler’s formula is one of the most famous in mathematics, his proof is virtually unknown by mathematicians today. There are several reasons for this. As we will see, Euler’s demonstration does not satisfy the modern standards of rigor. Also, there have been many proofs of Euler’s formula in the years since 1751 that are simpler and more transparent than Euler’s. Still, Euler’s proof is very clever and does not use metric properties of the polyhedra. The first truly rigorous justification was given four decades later, in 1794, by Legendre.10 In his surprising argument, which we present in chapter 10, Legendre used geometric properties of spheres.
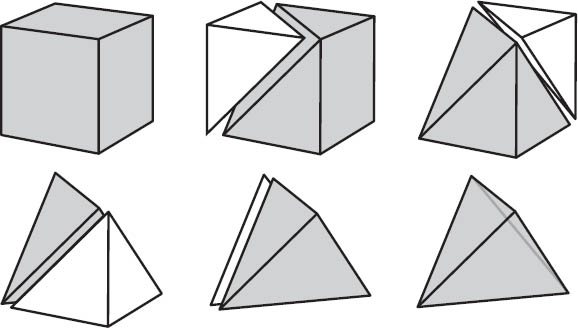
Figure 7.3. Removing vertices from a cube to obtain a tetrahedron.
Euler’s proof was a precursor to modern combinatorial proofs. He used the method of dissection to take a complicated polyhedron, perhaps containing many vertices, and systematically reduce it to a simpler polyhedron. Euler proposed that we remove vertices from the polyhedron, one at a time, until only four remain, leaving a triangular pyramid. By keeping track of the number of vertices, edges, and faces at each stage, and by using the known properties of the triangular pyramid, he was able to conclude that V − E + F = 2 for the original polyhedron.
Before jumping into Euler’s proof, we look at an example. Consider the decomposition of the cube shown in figure 7.3. At each stage we remove a vertex of the cube by cutting away a triangular pyramid, continuing until we obtain a single triangular pyramid. Because the cube is a relatively simple polyhedron, we are able to remove each vertex by slicing away a single pyramid. In general, however, we may have to cut away several pyramids to remove a single vertex. Table 7.1 shows the number of vertices, edges, and faces at each stage of the decomposition.
One might hope that as the number of vertices decreases, the numbers of faces and edges decrease with some predictable pattern. As we can see in the chart, however, the sequence has no obvious order. In this example the number of faces increases before decreasing—the polyhedron begins with six faces, then as the vertices are cut away the polyhedron has seven, then seven, then six, then four faces. This road seems to be a dead end. The key to Euler’s proof is his astute observation that the difference between the number of edges and the number of faces decreases by one after a vertex is removed (as we see in the right-most column of the table). As we shall see, this is the heart of Euler’s proof.
TABLE 7.1:
The decomposition of a cube to a tetrahedron by removing vertices one at a time.


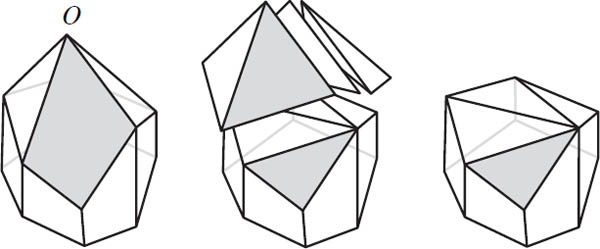
Figure 7.4. Remove the vertex O by cutting away pyramids.
We begin with a polyhedron having V vertices, E edges, and F faces. Our first task is to remove a vertex from the polyhedron so that the resulting polyhedron has one fewer vertex than the original. After doing so, we must determine the number of faces and edges of the resulting polyhedron. Let O be the vertex that is to be removed, and suppose n faces (and therefore n edges) meet at O. Euler saw that O can be removed by cutting away n − 2 triangular pyramids that have O as a vertex. For example, the polyhedron in figure 7.4 has a vertex formed from 5 faces, and it is removed by cutting away 3 pyramids.
Figure 7.5. A nontriangular face contributes one new face and one new edge to the new polyhedron.
We would like to know the number of faces and the number of edges in the reduced polyhedron. As we saw with the cube, there is no simple answer. We must look at three special cases. We look at the simplest case first: assume that all of the faces meeting at O are triangular. By cutting away O we remove these n faces, but beneath the n − 2 cut-away pyramids we find n − 2 new triangular faces. Assuming that all of these new triangular faces lie in different planes, the number of faces in our new polyhedron is
F − n + (n − 2) = F − 2,
where F is the original number of faces.
During this process we also remove the n edges that meet at the vertex O, but we add the n − 3 edges that lie between the n − 2 new triangular faces. Thus, the number of edges in the new polyhedron is
E − n + (n − 3) = E − 3,
where E is the original number of edges.
Looking again at the example in figure 7.4, we began with a polyhedron having 11 faces and 20 edges. After removing the three pyramids we have a new polyhedron with 11 − 2 = 9 faces and 20 − 3 = 17 edges.
In the previous argument, we made two assumptions about the decomposition of the polyhedron. One was that all of the faces meeting at O are triangular, and the other was that the new triangular faces of the polyhedron are not coplanar. Now we must examine what happens if either or both of these assumptions do not hold.
Suppose one of the faces meeting O is not triangular (e.g. the shaded face in figure 7.5). Then, when the triangular pyramid that shares this face is removed, the face does not completely disappear from the polyhedron. Also, a new edge is added where the face is cut in two. Thus, the number of faces and edges in the new polyhedron are both one larger than previously anticipated. In this example we begin with a polyhedron having 12 faces and 23 edges. After the three pyramids are removed, we obtain a polyhedron with 12 − 2 + 1 = 11 faces and 23 − 3 + 1 = 21 edges. In general, if the original polyhedron has s nontriangular faces meeting at O, then the number of faces and edges will be s larger than expected. So the number of faces is F − 2 + s and the number of edges is E − 3 + s.

Figure 7.6. Two coplanar faces decrease the number of faces and edges by one.
On the other hand, suppose that two of the new triangular faces are situated next to each other and lie in the same plane (e.g., the shaded faces in figure 7.6). Then they will not yield two distinct faces in the resulting polyhedron, but a single quadrilateral face. Thus, there will be one fewer face than was anticipated. Because there is no edge between these two faces, there will also be one fewer edge. In the example in figure 7.6 we begin with a polyhedron having 11 faces and 20 edges. After the pyramids are removed there are 11 − 2 − 1 = 8 faces and 20 − 3 −1 = 16 edges. If this happens t times, then there will be t fewer faces and t fewer edges than anticipated. So, in the resulting polyhedron, the number of faces is F − 2 + s − t and the number of edges is E − 3 + s − t.
These complicated-looking formulas represent the number of faces and the number of edges after a single vertex has been removed. The idea of keeping a running tally after several vertices are removed is daunting. However, Euler’s important observation saves us from having to keep track of these values. If we take the number of edges on the new polyhedron and subtract the number of faces we obtain
(E −3 + s − t) − (F − 2 + s − t) = E − F − 1.
In other words, the difference between the number of edges and the number of faces is exactly one less than it was before the vertex was removed. After n vertices have been removed, the difference in the number of edges and the number of faces is E − F − n.
With this, we can conclude Euler’s proof. We began with a polyhedron with V vertices, E edges, and F faces. Suppose that we remove vertices one at a time, n in all, until only four vertices remain. Then V − n = 4, or n = V − 4. The only polyhedron with four vertices is a triangular pyramid (which has four faces and six edges). For a triangular pyramid, the difference in the number of edges and the number of faces is 6 − 4 = 2, but from the previous discussion we know that it is also E − F − n. Thus we have the equations
E − F − n = 2
and
n = V − 4.
Substituting the second equation into the first and rearranging terms, we obtain V − E + F = 2, as desired.
At the outset, we claimed that Euler’s proof is not completely rigorous and that he overlooked some subtleties. In fact, we see that Euler was very careful about keeping track of the numbers of faces and edges when a vertex was removed, However, he was too cavalier with the process of removing vertices, for he did not give detailed instructions about how to cut away the pyramids. Instead he made do with a few vague examples. Euler stated, correctly, that there may be several ways to remove a given vertex by cutting away pyramids, but he raised no warning flags that some decompositions are acceptable and others must be avoided. He left the reader with the incorrect impression that any decomposition will work as well as any other. In fact, some get us into trouble.
The first snag we encounter is that a decomposition may inadvertently yield a polyhedron that is nonconvex. Euler gave an example in which the vertex to be removed, O, has four adjacent vertices A, B, C, and D (see figure 7.7). He wrote:
This can be done in two ways . . . two pyramids will have to be cut away, either OABC and OACD or OABD and OBCD. And if points A, B, C, D are not in the same plane the resulting solids will have a different shape accordingly.11
Figure 7.7. Removing a vertex from a polyhedron (left) may yield a convex (middle) or nonconvex (right) polyhedron.

Figure 7.8. Euler’s technique, applied to the polyhedron on the left may (middle) or may not (right) produce a degenerate polyhedron.
This is true, but if the four neighboring vertices are not coplanar, then one of the resulting polyhedra will necessarily be convex and the other one will be nonconvex. For the polyhedron in figure 7.7, removing pyramids OABD and OBCD will produce a nonconvex polyhedron.
Euler never mentioned convexity in his paper. He made the unstated assumption that all polyhedra are convex. If we look closely at his algorithm, we see that it is important that these polyhedra remain convex after a vertex has been cut away. Obtaining a nonconvex polyhedron can lead to trouble, for it may be impossible to use Euler’s technique to remove a vertex located at a point of nonconvexity. Or we can encounter worse trouble than this.
As the mathematician Henri Lebesgue (1875–1941) pointed out, not only can the resulting polyhedron be nonconvex, it may not be a polyhedron at all!12 In figure 7.8 we see a vertex of a polyhedron that meets four faces. As with the previous example, we can remove this vertex in two different ways. One of the two methods works fine, but the other method yields a shape that is not a polyhedron, but rather an object consisting of two polyhedra joined along an edge. To make matters worse, this non-polyhedron does not satisfy Euler’s formula (V = 6, E = 11, F = 8, so V − E + F = 3, not 2). This example seems to indicate a serious shortcoming in Euler’s proof. In figure 7.9 we see that by applying Euler’s dissections we can obtain other degenerate polyhedra. One decomposition yields two polyhedra joined at a vertex, and the second yields a disconnected polyhedron. Again, these objects fail to satisfy Euler’s formula.

Figure 7.9. More problems with Euler’s technique.
It turns out that Euler’s proof is not beyond hope. With a little care we can repair his argument.13 In all of the examples that we gave, making a wrong choice during the decomposition led to a breakdown of his proof; but in each case, there was a decomposition that was acceptable. We can prove that by making strategic, and not arbitrary, choices, we can remove a vertex in a way that guarantees that the resulting object is a convex polyhedron, thereby saving the day. So, after these repairs, we may finally assert that Euler’s formula holds for all convex polyhedra.
Since Euler presented his proof, there have been many new proofs, most of which are more straightforward than his. We will see several of these in this book.
The subtle convexity problem turned out to be a real challenge for mathematicians to understand. It was the source of decades of interesting research, as mathematicians sought to determine exactly what properties a polyhedron must possess in order to satisfy Euler’s formula. As we will see, they looked at nonconvex polyhedra, polyhedra with holes, and other, more pathological examples. This line of inquiry turned out to be extremely fruitful.
It took many years for mathematicians to see the importance of something that was apparent to Euler—that this theorem was about dimension and the rules for building mathematical objects. Euler’s formula and its generalizations became the cornerstone for the field of topology.
It is likely that Euler had no idea of the importance of his theorem. He never returned to the problem of classifying polyhedra and he never wrote about the polyhedron formula again. He would never know that it would be one of his most beloved contributions to mathematics.