CHAPTER 14
IT’S A COLORFUL WORLD
The mathematician Charles Lutwidge Dodgson (1832–1898), better known as Lewis Caroll, author of Alice in Wonderland, invented the following two-person game. Person A draws a map of a continent with any number of countries. Then person B colors the map so that neighboring countries (they have to share a border, touching at a corner does not count) have different colors. The object of the game is for A to draw a map so complicated that it forces B to use many colors. B, meanwhile, has to figure out how to color the map with as few colors as possible.
A simple map resembling a chess board can be colored using only two colors, but even the most unskilled map-drawer can force three colors. It is also not difficult to draw a map requiring four colors—simply draw a country surrounded by exactly three others (such as how Luxembourg is surrounded by Germany, France, and Belgium). Because all four countries are mutual neighbors, four colors are necessary (Paraguay and Malawi are two other examples).
In the introduction we saw a more subtle way to force four colors. Four colors are necessary to color Nevada, California, Arizona, Utah, Idaho, and Oregon because Nevada is surrounded by an odd number of states (figure 14.1). It turns out that Nevada, West Virginia, and Kentucky are the only such problem states in the United States. By carefully coloring these states and their neighbors, it is possible to extend the coloring to the entire United States using a fourth color only two times.

Figure 14.1. The map of the United States can be colored using four colors.

Figure 14.2. Disconnected countries can force five colors.
Can person A do better than that? Can A force B to use five colors? As we will discuss shortly, it is impossible to find five mutually adjacent countries (we decide in advance that we do not allow disconnected “imperialistic” nations, such as country a in figure 14.2). Is that enough to ensure that four colors are sufficient for coloring any map?
According to folklore, mapmakers were the first to notice that four colors sufficed to color any map. There is no evidence to support this assertion. If they were aware of it, they did not publicize it. Kenneth O. May scoured numerous books on cartography and the history of map making and found no mention of the four color theorem.2 A quick perusal of an atlas shows that most maps are colored using either one color or many colors. There is no indication that mapmakers felt any compulsion to minimize the number of colors used.
As far as anyone can tell, the observation dates back to 1852. Francis Guthrie (1831–1899), a recent graduate in mathematics, recognized that all the counties in England could be colored using only four colors, and he wondered if this was always true. He formulated the conjecture that would become one of the trickiest and most well-known problems in all of mathematics: the four color conjecture.
FOUR COLOR CONJECTURE
Every map can be colored with four or fewer colors so that no neighboring nations are the same color.
Francis Guthrie mentioned this observation to his brother Frederick, who in turn shared it with his professor, the respected mathematician Augustus De Morgan (1806–1871). De Morgan was intrigued. On October 23, 1852, he wrote to Sir William Rowan Hamilton (1805–1865):
A student of mine asked me today to give him a reason for a fact which I did not know was a fact—and do not yet. He says that if a figure be anyhow divided, and the compartments differently colored so that figures with any portion of common boundary line are differently colored—four colors may be wanted, but not more . . . Query cannot a necessity for five or more be invented? . . . What do you say? And has it, if true, been noticed? . . . The more I think of it the more evident it seems. If you retort with some very simple case which makes me out a stupid animal, I think I must do as the Sphynx did.3
Fortunately for De Morgan, he did not have to leap to his death as did the Sphynx after Oedipus answered her riddle correctly. Indeed, Hamilton was not even tempted by the problem. He replied, “I am not likely to attempt your ’quaternion of colors’ very soon.”4
Although De Morgan tried get a few other people to work on the problem, the mathematical community stubbornly refused to embrace it. Nothing appeared in print for almost twenty years. The tipping point for the four color problem was on June 13, 1878, when, at a meeting of the London Mathematical Society, the esteemed mathematician Arthur Cayley asked if the problem had been solved and admitted that he could not do it. The question was then printed and distributed widely in the Society’s proceedings.5
This problem has been a favorite of mathematical enthusiasts ever since Cayley brought it to the attention of the world. The beauty of the question is that it is so easy to state that a young child could understand it. It is a mathematics problem, to be sure, but it requires no arithmetic, algebra, trignometry, or calculus. Its proof seems tanatalizingly within reach. As renowned geometer H. S. M. Coxeter (1907–2003) wrote:
Almost every mathematician must have experienced one glorious night when he thought he had discovered a proof, only to find in the morning that he had fallen into a similar trap.6
While at Scientific American, Martin Gardner used to receive one lengthy proof of the four color conjecture every few months (all flawed, of course). So in 1975, when he decided to write an April Fools’ Day column, he included the four color conjecture. In his article “Six Sensational Discoveries that Somehow or Another have Escaped Public Attention,” he reported on six major discoveries of 1974, one of which was a counterexample to the four color conjecture. The caption under the 110-region map said it all: “The four-color-map theorem is exploded.”7 The joke was lost on many readers, however. He received over a thousand letters about this article, including more than a hundred colored copies of the “counterexample,” from dupes who did not recognize the hoax.
Although we now attribute the four color problem to Francis Guthrie, many older texts erroneously give credit to the German mathematician August Möbius (1790–1868). Möbius, a descendant of Martin Luther, was a quiet and reserved family man. As an adult he did not travel often, but as a graduate student he attended Leipzig University, the University of Göttingen (he worked with Gauss for two semesters), Halle University, and then back to Leipzig where he completed his doctoral thesis in astronomy. After this period of frequent relocations, he vowed to remain in his beloved Saxony. Despite repeated job offers from other universities, he stayed at Leipzig for the rest of career.
At Leipzig Möbius worked as an astronomer and oversaw their observatory. He loved mathematics, and it was in mathematics, not astronomy, that he made his most important contributions. He is best known for his work on barycentric calculus, projective and affine geometry, and the foundations of topology. His solitary and careful approach to mathematics produced fine work, but did not make him a gifted lecturer. Because of this, very few fee-paying students attended his classes.
The source of this misattribution is a story told by one of Möbius’s students, Richard Baltzer (1818–1887). Baltzer wrote that in 1840 Möbius posed to his class the problem of the five princes. He described it as follows:

Figure 14.3. August Möbius.
There was once a king in India who had a large kingdom and five sons. In his will he decreed that, after his death, the kingdom should be divided among his sons in such a way that the territory of each should have a common boundary line (not merely a point) with the territories of the remaining four. How was the kingdom divided?8
The following day Möbius confessed to his frustrated students that the problem was impossible as stated.
Given what we know, it is easy to deduce the impossibility of a solution. Suppose there was a way to divide the kingdom into five such regions, and in each region was the prince’s palace. Then for each pair of brothers it is possible to build a road between their two palaces so that the road does not cross the other brothers’ land. However, this creates a planar graph with palaces as vertices and roads as edges. Specifically, it is the complete graph on five vertices, K5, which we proved is not planar.
In a postscript Baltzer drew the false conclusion that the impossibility of this solution implies that the four color theorem is true. He wrote, “How delighted Möbius would have been to see such a far-reaching application” of this problem.9 The tenuous link between the five-princes problem and the four color problem is that if such a partitioning of the kingdom existed, then (just like the map in figure 14.2) it would be impossible to color the map with only four colors. However, in reality this eliminates only one of the barriers in the proof of the four color theorem. It may still be possible to produce a complicated map without five mutually neighboring regions that cannot be colored with four colors. According to Martin Gardner, many of the false proofs of the four color theorem that arrived in his mailbox were nothing more than the five-princes problem in disguise.

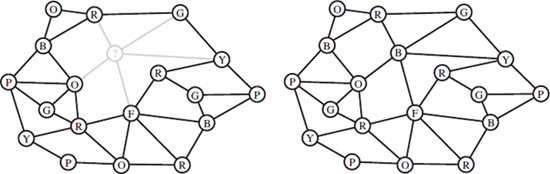
Figure 14.4. The adjacency graph for a map.
We should not toss out Möbius’s puzzle entirely. The technique of joining palaces by roads is actually a useful one. Just as with the Königsberg bridge problem, the precise geography of the countries is irrelevant; all that is important are the relative locations. It is a topological problem that can be repackaged in terms of graph theory.
The adjacency graph of a map has one vertex for each country, and two vertices are joined by an edge whenever the corresponding countries share a border (see figure 14.4). If two countries share more than one border, we still draw only one edge between the corresponding vertices.
Adjacency graphs have some nice properties. It is not difficult to see that the adjacency graph of any map is planar. Simply take the vertices to be the capitals of the countries and the edges to be roads between the capitals that stay inside the two countries. By construction, an adjacency graph will be devoid of loops and parallel edges; such a graph is called simple. In short, an adjacency graph for a map is a simple planar graph. Notice that if the map is connected, then the adjacency graph will be, as well.
When we create the adjacency graph for a map, we transform a map-coloring problem into a graph-coloring problem. Instead of coloring the countries of the map, we color vertices of the graph. If a map (or graph) can be colored using n colors so that neighboring countries (vertices) have different colors, we will say that it is n-colored. We may restate the four color conjecture as follows.

Figure 14.5. Coloring the adjacency graph gives a coloring of the map.
FOUR COLOR CONJECTURE FOR PLANAR GRAPHS
Every simple planar graph can be 4-colored.
In figure 14.5 we see the map of Nevada and its neighbors and the associated adjacency graph. We color the graph using four colors, then transfer this coloring to the original map.
In a typical map there may be countries with many neighbors, but this is impossible for all countries. In any map there must be some country that has five or fewer neighbors. We call this important fact the five neighbors theorem. The proof of the five neighbors theorem uses Euler’s formula and a little counting. In terms of graphs we state it as follows.
FIVE NEIGHBORS THEOREM
Every simple planar graph has a vertex of degree five or less.
Suppose we have a simple planar graph. Because the graph has no loops or parallel edges, we can add edges to it so that every face is bounded by exactly three edges. We will prove that this (larger) triangulated graph has a vertex of degree 5 or less, and therefore so must the (smaller) original graph. Suppose the triangulated graph has V vertices, E edges, and F faces (counting the exterior region as a face). Each edge borders two faces and each face is bounded by three edges, so 3F = 2E. By Euler’s formula V − E + F = 2, or equivalently, 6E − 6F = 6V − 12. Substituting 4E for 6F we obtain
2E = 6V − 12.
Because each edge has two endpoints, the sum of the degrees of all vertices is 2E. So the average degree of the vertices is

Of course, because the average degree is less than six, there must be at least one vertex of degree five or less.
To show how the five neighbors theorem is useful in graph-coloring problems, we will prove the six color theorem.
SIX COLOR THEOREM
Every map can be colored with six or fewer colors.
For the sake of contradiction, assume that this statement is false. Then there are one or more maps that cannot be six-colored. Survey this collection of nasty maps and find one that has the fewest number of countries. Suppose this map has N countries. Such a smallest counterexample is often called a minimal criminal. The benefit of singling out a minimal criminal is that we can say with certainty that any map with N − 1 or fewer countries can be six-colored.
Consider the adjacency graph G for this minimal criminal. By the five neighbors theorem, there is some vertex v in G with degree five or less. Remove y and all edges incident upon v from G to obtain a new graph H. It is not difficult to see that H is the adjacency graph for a map with N − 1 countries. Since H has N − 1 vertices, it can be six-colored. Now, put the vertex and edges back into the graph. Since v is adjacent to at most 5 other vertices, there is at least one unused color remaining to color v. Thus it is possible to six-color G. This contradicts our assumption that G was a minimal criminal, so every map is six-colorable. In figure 14.6 we use this technique to color a graph using red, blue, yellow, green, purple, and orange.
Unfortunately, this same proof does not work when there are only four or five colors available. When it comes time to reinsert the vertex v, there may be no color remaining to color the vertex. We must employ a more subtle trick for these cases.
One such trick was discovered by Alfred Bray Kempe (1849–1922). On July 17, 1879, Kempe, a student of Cayley’s, announced that he had a proof of the four color conjecture, and his proof was published later that year.10
Figure 14.6. Six-coloring a minimal criminal.

Figure 14.7. Alfred Bray Kempe.
Unlike most of the false proofs that followed in the next hundred years, Kempe’s proof was very convincing. He introduced clever new techniques to that enabled him to color the remaining vertex of the minimal criminal. The mathematical community was thrilled by the proof.
Kempe’s proof remained the final word on the four color conjecture for a decade. Unfortunately for Kempe, the case was not yet closed. In 1889 Percy John Heawood (1861–1955) discovered an error in Kempe’s argument. It turned out to be a fatal flaw. Heawood produced a map for which Kempe’s logic fell appart. In his published note, which appeared in 1890, Heawood wrote:
The present article does not profess to give a proof of this original Theorem; in fact its aims are so far rather destructive than constructive, for it will be shown that there is a defect in the now apparently recognized proof.11
Figure 14.8. Interchanging the colors of a red-blue chain produces another valid coloring.
And so the four color theorem became the four color conjecture again.
Although Kempe’s proof was wrong, the techniques he introduced were very important. Heawood acknowledged that Kempe’s ideas were sufficient to prove the five color theorem. In fact, they were essential ingredients in the eventual proof of the four color theorem. Although this false proof may have been an embarrassment to Kempe, it did not permanently damage his career. He continued to be an active member of the Royal Society (he had been elected for mathematical work unrelated to the four color theorem) and he was later knighted.
As anyone who has tried to four-color a large map knows, it is easy to color the map for a while but then get stuck so that it is impossible to complete the coloring.* At this point the colorer must back up and re-color parts of the map. The trick that Kempe gave us is an easy way to recolor a map.
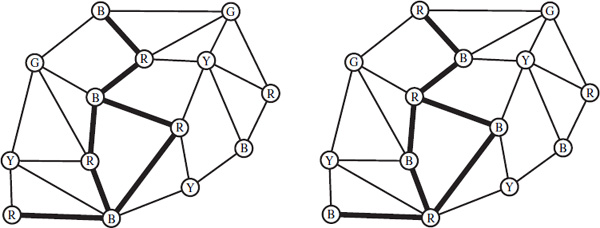
Start with any colored (or partially colored) graph. Pick two colors, say red and blue, and a vertex of one of these colors. Follow all the possible paths from this vertex that pass through a blue vertex, a red vertex, a blue vertex, and so on. This collection of red and blue vertices is called a red-blue chain, or a Kempe chain (see figure 14.8). Notice that a Kempe chain is often not linear; it may have branches or loops. The key observation is that because no vertex adjacent to such a Kempe chain is red or blue, we may change every red vertex in the chain to blue and every blue vertex in the chain to red and still have a valid coloring of the graph.

Figure 14.9. Interchange the colors of the red-yellow chain to complete the coloring.
Earlier we proved the six color theorem. This trick of Kempe’s enables us to prove the five color theorem.
FIVE COLOR THEOREM
Every map can be colored with five or fewer colors.
We begin the proof in exactly the same way that we did for the six color theorem. Suppose we have a minimal criminal—a map with the fewest number countries, N, that cannot be five-colored. Again, by the five neighbors theorem there is a vertex v in the adjacency graph G that has degree five or less. Let H be the graph obtained by removing the vertex v. Because H has N − 1 vertices, it can be five-colored. Consider the vertices adjacent to v. If there are 4 or fewer colors used to color these vertices (for instance, if the degree of v is 4 or less), then we may complete the coloring by choosing an unused color to color v. If the vertices adjacent to v use all five colors then our solution is not so simple.
Suppose the vertices adjacent to v are named a, b, c, d, and e (labeled clockwise), and they are colored red, blue, yellow, green, and purple, respectively. Consider the red vertex a and the red-yellow chain containing it. There are two cases to examine. First, as in figure 14.9, suppose that vertex c is not in this red-yellow chain. Then we can interchange the red and yellow vertices in the chain without changing the color of vertex c. In particular, we can then color v red and obtain a five-coloring of G.
On the other hand, suppose c is in this red-yellow chain (as in figure 14.10). Then changing the colors in the chain would also change the color of c and not free up a color for v. This would not help at all.
Figure 14.10. Interchange the colors of the blue-green chain to complete the coloring.
However, because the graph is planar, the blue-green chain containing vertex d cannot contain the vertex b. Thus, interchanging the colors in this blue-green chain allows v to be colored green, and we obtain a five-coloring of G.
Kempe’s faulty proof of the four color theorem was similar to this proof of the five color theorem. However, the argument was necessarily more subtle. It was possible to have a vertex v of degree 5 surrounded by vertices of four different colors. He had to recolor one or two Kempe chains to decrease that number to three so that he could color v. Although his method looked correct, he missed one case where recoloring two Kempe chains could yield an inadmissible coloring.
The popularity of this fascinating problem continued to enthrall mathematicians and novices alike. Notable mathematicians such as George D. Birkhoff (1884–1944), Hassler Whitney (1907–1989), Henri Lebesgue (1875–1941), and Oswald Veblen (1880–1960) threw their hats in the ring. Despite their long lists of accomplishments, these giants were unable to crack the difficult problem. Some well-respected mathematicians, such as H. S. M. Coxeter, even expressed doubts that the conjecture was true.
As the twentieth century progressed, attention turned to unavoidable sets and reducible configurations. An unavoidable set is a collection of configurations, at least one of which must be present in every adjacency graph. For example, the five neighbors theorem gives us the simplest unavoidable set, shown in figure 14.11—there must be a vertex of degree less than six.
On the other hand, a reducible configuration is a collection of vertices and edges that cannot appear in a minimal criminal. By using the method of Kempe chains it is easy to show that the first four configurations in figure 14.11 are reducible. We can remove the vertex, color the rest of the graph, recolor once using Kempe chains, if necessary, then color the last vertex. The fifth one is the problem.

Figure 14.11. An unavoidable set of configurations.
Thus, the goal became finding an unavoidable set of reducible configurations. Doing so would prove the four color theorem because it would be a collection of configurations that could not appear in a minimal criminal, yet must appear in every adjacency graph. This would produce a contradiction to the existence of a minimal criminal.
On July 22, 1976, almost a century after Kempe’s failed proof, two researchers from the University of Illinois, Kenneth Appel (b. 1932) and Wolfgang Haken (b. 1928), announced that they had found an unavoidable set containing 1,936 reducible configurations. By the time their two papers appeared the following year they were able to simplify their work and remove redundancies, reducing the number to 1,482.13 (They also added a third author to one of the papers, John Koch, for his help with computations.) The four color theorem had fallen, at last!
FOUR COLOR THEOREM
Every map can be colored with four or fewer colors.
At the end of the summer of 1976 Haken presented their work to the attendees of a joint meeting of the American Mathematical Society and the Mathematical Association of America. At the end of the lecture the audience did not burst into applause, whoop for joy, or enthusiastically pat Haken on the back. Instead, they responded with polite applause. For the roomful of theoretical mathematicians, the much-anticipated conclusion to one of the most interesting stories in mathematics was extremely anticlimactic.
The reason for the cool response was that after Appel and Haken compiled the graph configurations, which filled seven hundred handwritten pages, they plugged them into a computer and let it check the many thousands of special cases. The work of the computer was not even remotely checkable by hand. The computations took six months, used over one thousand hours of computer time, and produced a stack of printouts four feet tall. Although most people came to believe that their proof was correct, most pure mathematicians found the proof inelegant, unsatisfying, and unsporting. It was as if Evel Knievel boasted that he could cross the Grand Canyon on his motorcycle, only to build a bridge and use it to make the crossing. Perhaps it is how mountain climbing purists feel about the use of bottled oxygen in high-altitude climbing.

Figure 14.12. Kenneth Appel and Wolfgang Haken.
Scientists and engineers have used computers to solve countless problems, but mathematicians have not. Computers are good at making speedy calculations, but not at the kind of precise and subtle arguments that are required in mathematical proofs. Like writing, philosophy, and art, mathematics has always been a human endeavor, one that cannot be automated. Perhaps some day someone will create a black box that proves theorems. We put a statement in, and the black box says “true” or “false.” (There are some early attempts at this.) Some would say that this would take the fun out of mathematics and make it less beautiful.
The four color proof was the first high-profile computer-assisted proof. These show no inclination of going away. Another controversial example is Thomas C. Hales’s 1998 proof of the Kepler conjecture.14 Hale proved that Kepler was correct when he claimed that the most efficient way to pack spheres in a box is by staggering them in a crystalline pattern, just as grocers do with oranges or artillerymen did with cannon balls. Although the result appeared in the prestigious Annals of Mathematics, it took years for the journal to agree to publish it (it came to press in 2005), and even then the editors said that they did not and could not verify the thousands of lines of computer code.
In the years since Appel and Haken unveiled their controversial proof, it has been independently verified. Other mathematicians have found smaller unavoidable sets of reducible configurations and have discovered more efficient ways of proving the theorem, but thus far every proof has required computer verification.
Paul Erdős (1913–1996), the famously eccentric Hungarian mathematician, used to speak of “The Book”—the imaginary tome that contains the most beautiful and elegant proofs of mathematical theorems. Today the door to the four color theorem is almost closed, but we are still waiting for an old fashioned, pencil-and-paper verification—we have not yet seen the proof from The Book.
* Stephen Barr suggested a two-person game along these lines. The first player draws a country and colors it one of four colors. The second player adds a country and colors it. Play alternates in this way until one player is forced to use a fifth color.12