CHAPTER 15
NEW PROBLEMS AND NEW PROOFS
Suppose you were asked: what trees change color and lose their leaves in the autumn? If you replied, “Maple trees do,” then you would have given a correct answer. However, anyone who has driven through the Pennsylvania countryside in October knows that there are also radiantly colored oak, birch, and beech trees standing amid beds of fallen leaves. So, although the answer was correct, it did not give a complete account of all such trees. Could you say that all trees change color in the autumn? No. Pine, fir, spruce, and cedar trees have no leaves to lose. In order to make a general, but true, statement, one must look closely at numerous trees. A more complete answer would be: deciduous trees change color and lose their leaves in the autumn.
Convex polyhedra satisfy V − E + F = 2. This is a true statement. We know this from the proofs of Euler, Legendre, Cauchy, and others. However, we know that this is not the best we can do. As Poinsot pointed out, Euler’s formula holds for more polyhedra than just those that are convex—star-convex polyhedra, for instance. The mathematician D. M. Y. Sommerville (1879–1934) wrote, “Convexity is to a certain extent accidental, and a convex polyhedron might be transformed, for example, by a dent or by pushing in one or more of the vertices, into a nonconvex polyhedron with the same configurational numbers.”2 So, it is misleading and needlessly simplistic to say that convex polyhedra are the only ones that satisfy Euler’s formula. Ernest de Jonquières believed that “in invoking Legendre, and like high authorities, one only fosters a widely spread prejudice that has captured even some of the best intellects: that the domain of validity of the Euler theorem consists only of convex polyhedra.”3
Can we go so far as to say that Euler’s formula holds for all polyhedra? No, just as there are trees that do not change color in the autumn, there are polyhedra that do not satisfy Euler’s formula. We would like to determine exactly what properties a polyhedron must possess to satisfy Euler’s formula. The mineralogist Johann Friedrich Christian Hessel (1796–1872), whom we will meet shortly, called such polyhedra Eulerian.
As we discussed in chapter 2, mathematicians worked with polyhedra for many centuries without having a proper definition. They were safe so long as they assumed (almost always implicitly) convexity, but once they tried to claim that something was true for all polyhedra, they generally ran into trouble. The need for a rigorous definition of polyhedra came to a head in the early nineteenth century.
The first person to look carefully at which polyhedra satisfy the polyhedron formula was Simon-Antoine-Jean Lhuilier (1750–1840). Perhaps Lhuilier was destined to work on Euler’s formula. Like Euler, Lhuilier was Swiss, and the year of his birth was the year that Euler discovered the polyhedron formula. Most amusingly, the literal translation of l’huilier is “the oilcan” or “the one who oils,” so Lhuilier may be called “The Oiler.”
Like Euler, Lhuilier was tempted away from the clergy by mathematics. When Lhuilier was young, one of his relatives offered to leave him part of his fortune if he pursued a career in the church. Instead of taking this generous offer, Lhuilier decided to become a mathematician.
Lhuilier spent the early part of his mathematical career in Warsaw as a tutor for the son of Prince Adam Czartoryski. Afterward he returned to Switzerland where he took a position at the Geneva Academy, eventually rising to the level of rector. During his long life he contributed to geometry, algebra, and probability, and from this work he received international recognition. He also wrote popular textbooks that were used for many years in Poland. About his personality one biographer wrote, “Whereas the Poles found Lhuilier distinctly puritanical, his fellow citizens of Geneva reproached him for his lack of austerity and his whimsicality, although the latter quality never went beyond putting geometric theorems into verse and writing ballads on the number three and on the square root of minus one.”4
In 1813 Lhuilier made an important contribution to the theory of polyhedra and to understanding Euler’s formula. In his paper he presented three classes of polyhedra that failed to satisfy the polyhedron formula. He called them “exceptions.”
Lhuilier’s paper was published in the new, privately-established journal Annales de mathématiques pures et appliquées.This journal, the first one dedicated solely to mathematics, was founded and edited by the French artillery officer and accomplished geometer Joseph Diaz Gergonne. As the mathematician Jean-Claude Pont wrote, Gergonne “had the detestable habit to publish, of work that one submitted to him, only the parts that interested him.”5 Not only did Gergonne edit Lhuilier’s work substantially, he repeatedly interjected his own comments into the text of Lhuilier’s article—even the assertion that he knew two of the three exceptions before reading Lhuilier’s paper!

Figure 15.1. Lhuilier’s exceptions: annular faces, tunnels, and cavities.
The first class of exceptions presented by Lhuilier consisted of polyhedra with annular, or ring-shaped, faces. For instance, in figure 15.1 an indentation in the middle of one face of a cube produces a face in the shape of a square washer. This polyhedron has 13 vertices, 20 edges, and 10 faces (5 square faces, 4 triangular faces, and the single annular face). In this case Euler’s formula does not hold because 13 − 20 + 10 = 3. Lhuilier did not call these faces annular or ring-shaped. He remarked that the face has an “inner polygon.”
The second class of exceptions presented by Lhuilier is polyhedra with one or more “tunnels” bored through the center. In figure 15.1 we see a polyhedron in the shape of a polyhedral doughnut. In this example the polyhedron has 16 vertices, 32 edges, and 16 faces, thus 16 − 32 + 16 = 0.
The inspiration for the third class of exceptions came from one of Lhuilier’s friend’s mineral collection. In one of the specimens Lhuilier saw a colored crystal suspended inside a clear crystal. (Later in 1832, Hessel was also inspired by such a crystal—in his case a lead sulphide cube within a calcium chloride crystal.) Lhuilier imagined a polyhedron with a polyhedron-shaped cavity in the interior. Of course this exception only makes sense if a polyhedron is assumed to be solid and not hollow. A cube with a cube-shaped cavity is shown in figure 15.1. This polyhedron has 16 vertices, 24 edges, and 12 faces, and 16 − 24 + 12 = 4.
Figure 15.2. Complicated polyhedra.
Lhuilier (and Gergonne) believed that this collection encompassed all of the possible exceptions to Euler’s formula. Lhuilier wrote, “One will easily be convinced that Euler’s theorem is true in general for all polyehdra, whether they are convex or not, except for those instances that will be specified.”6
Then, rather than ignoring the exceptions, Lhuilier devised a modification of Euler’s formula that took into account the features of his exceptional polyhedra. He asserted that a polyhedron with T tunnels, C cavities, and P inner polygons satisfies
V — E + F = 2 − 2T + P + 2C.
A quick count shows that this formula is indeed valid for the three polyhedra in figure 15.1.
It turns out, however, that Lhuilier’s three exceptions do not include all of the possible exceptions to Euler’s formula, and that his insightful formula does not apply to all “exotic” polyhedra. For instance, the four polyhedra in figure 15.2 do not fit into Lhuilier’s three categories and it is not clear how to apply his formula. The first polyhedron has a face with two inner polygons that share a common vertex; the second has a tunnel with a branch in it; the third has a cavity in the shape of a torus; and the fourth is shaped like a torus, but the tunnel is not obvious.
Again, we return to the problem of defining polyhedron—it is impossible to classify Eulerian polyhedra without first having an accurate definition of polyhedron. Nevertheless, Lhuilier’s classification of these exceptions was extremely important, and a suitably modified version of his formula would eventually be correct. In fact, according to Lakatos, this modified version of Euler’s formula, or one like it, was rediscovered a dozen times in the eighty years following Lhuilier’s discovery.
Johann Hessel was originally trained in medicine, but he changed his vocation after the noted mineralogist K. C. von Leonard urged him to become a mineralogist. Eventually Hessel became a professor of mineralogy and mining technology in Marburg, Germany. He made contributions to many areas of science, but he is most well known for his mathematical investigation of symmetry classes of minerals.

Figure 15.3. Hessel’s exceptions to the polyhedron formula.
In his paper of 1832 Hessel presented five exceptions to the polyhedron formula.7 When he wrote and submitted his paper, he was unaware of Lhuilier’s work from two decades earlier. Soon Hessel learned of Lhuilier’s work and learned that three of his five exceptions coincided with Lhuilier’s. Hessel believed that many people were unaware of these important exceptions, so he decided not to withdraw the publication. Hessel’s two new exceptions are shown in figure 15.3. One is a polyhedron formed from two polyhedra joined at an edge, and the other is a polyhedron formed from two polyhedra joined at a vertex. It is debatable whether these figures should be classified as polyhedra, but they surely fail to satisfy the polyhedron formula. The first has 12 vertices, 20 edges, and 11 faces (12 − 20 + 11 = 3) and the second has 8 vertices, 14 edges, and 9 faces (8 − 14 + 9 = 3).
Louis Poinsot found two more exceptions in 1810.8 In the same paper that contained the refinement of Legendre’s proof, Poinsot presented the four star polyhedra shown in figure 15.4. As we have seen, mathematics is often discovered, forgotten, and then rediscovered. Two of Poinsot’s four star polyhedra, the great and small stellated dodecahedra, were described by Kepler (see figure 6.6), and prior to that they appeared in the artwork of Jamnitzer and Uccello (figure 6.3). Poinsot was the first to present the other two star polyhedra, the great dodecahedron and the great icosahedron, in a mathematical context, although the former is also seen in the drawings of Jamnitzer (figure 6.3). These four polyhedra are now referred to as Kepler-Poinsot polyhedra.
Figure 15.4. The Kepler-Poinsot polyhedra: great and small stellated dodecahedra, the great dodecahedron, and the great icosahedron.
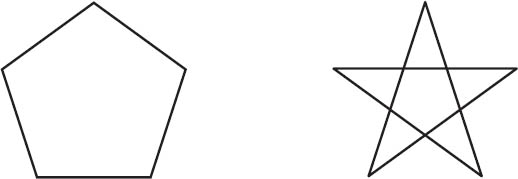
Figure 15.5. A regular pentagon and a regular self-intersecting pentagon, the pentagram.
The obvious way to view these is as nonconvex polyhedra formed from triangular faces. As we have already pointed out, they are star convex and thus, by Legendre’s proof, satisfy the polyhedron formula. However, neither Kepler nor Poinsot perceived them in this way. They saw these exotic polyhedra as new regular polyhedra.
In order to understand their point of view, we need to return to polygons in the plane. Earlier we asserted that there is only one regular n-sided polygon for each n > 2. For instance, the regular pentagon is shown in figure 15.5. However, if we were to loosen our requirements and allow the sides of the polygon to intersect, then we would find another regular pentagon—the pentagram of the Pythagoreans. After all, drawing a pentagram requires only five strokes of the pencil. We think of the pentagram as having five vertices and five sides joining these vertices. The edges happen to intersect two other sides, but we ignore these intersections and do not count them as vertices. The pentagram is formed by five sides of equal length and the angles between them are equal. It is very reasonable to call this polygon regular.
Kepler and Poinsot viewed their star polyhedra in this same way. Instead of forming the great dodecahedron out of triangles, we construct it from twelve self-intersecting pentagonal faces (see figure 15.6). That is, take all coplanar faces and join them to make a single face. In this way, the great dodecahedron is constructed from congruent regular pentagons and the same number of faces meet at each vertex. If we are willing to drop the convexity requirement, then the great dodecahedron can be considered a regular polyhedron, just like the Platonic solids. Likewise, the other three Kepler-Poinsot solids also have this redefined trait of regularity—the great and small stellated dodecahedra have pentagrams as faces and the great icosahedron has equilateral triangles as faces.
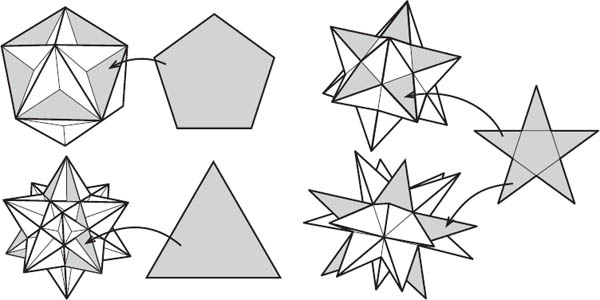
Figure 15.6. Regular polyhedra with self-intersecting faces.
It turns out that, just like Theaetetus proved that there are only five regular polyhedra, in 1811 Cauchy proved that only four polyhedra satisfy this new, relaxed definition of regularity—the four Kepler-Poinsot polyhedra.9
Although these are not everyday polyhedra, we can still compute V − E + F. Sure enough, the great icosahedron (V = 12, E = 30, F = 20) and the great stellated dodecahedron (V = 20, E = 30, F = 12) satisfy Euler’s formula. However, the other two do not—they are two more exceptions to Euler’s formula. Indeed, when we view the great dodecahedron as a polyhedron with twelve pentagonal faces, it does not satisfy the polyhedron formula. It has 12 vertices and 30 edges, thus 12 − 30 + 12 = −6. The small stellated dodecahedron also has 12 vertices, 30 edges, and 12 faces, so again the alternating sum yields −6.
The first half of the nineteenth century saw many exceptions to Euler’s formula, but it also saw many new proofs. By 1811 there were demonstrations by Euler, Legendre, and Cauchy. In 1813, in Lhuilier’s paper that contained his three exceptions,10 he gave a new proof that the polyhedron formula holds for convex polyhedra. Like Euler did, Lhuilier decomposed the polyhedron into pyramids. To do so, he placed a new vertex in the interior of the polyhedron and created edges and faces running from this vertex to the vertices and edges of the polyhedron. In this way he decomposed the polyhedron into many pyramids, all of which had a common vertex. Then he proved that the polyhedron formula holds for any pyramid and for solids constructed from pyramids in this way.
In Lhuilier’s paper Gergonne gave a proof for convex polyhedra (this same proof was rediscovered fourteen years later by Jakob Steiner [17961863]).11 Gergonne projects the polyhedron down onto the plane and uses an argument about the angles of the polygons.
One of the most clever proofs of the polyhedron formula is due to Karl Georg Christian von Staudt (1798–1867) in 1847. His proof had the special advantage that it applied to a broad class of nonconvex polyhedra.
Staudt was born into a noble family in Rothenburg, Germany. At the age of twenty he enrolled at the University of Göttingen to study astronomy and mathematics with Gauss. His PhD work in astronomy so impressed Gauss that he helped find Staudt a lecturing position at the University of Würzburg while Staudt was working as a secondary-school teacher. In 1835 Staudt became a full professor at the University of Erlangen, where he was the preeminent mathematician. Staudt was not a prolific mathematician, but in 1847 he wrote an influential book on projective geometry called Geometrie der Lage, which was later followed by three long supplements. It is for this work that he is best remembered.
Convexity is a sufficient condition for Euler’s formula, but as Poinsot pointed out, it is not necessary. In Geometrie der Lage Staudt finally gave a very general set of criteria that describe Eulerian polyhedra.12 Staudt implicitly assumed that his polyhedra were hollow shells, not solid. In addition, he made the following assumptions about his polyhedra:
1. It is possible to get from any vertex to any other vertex by a path of edges.
2. Any path of edges that begins and ends at the same vertex without visiting any vertex twice (recall that such a path is called a circuit) divides the polyhedron into two pieces.
Staudt’s insightful criteria include many polyhedra that are not convex. For instance, in figure 15.7 we see two very complicated polyhedra. The first, it turns out, satisfies all of Staudt’s criteria (indeed V = 48, E = 72, and F = 26, and 48 − 72 + 26 = 2). The second does not. Cutting along the darkened path of edges does not disconnect the polyhedron (for this polyhedron V = 40, E = 60, and F = 20, and 40 − 60 + 20 = 0).

Figure 15.7. Two complicated polyhedra.

Figure 15.8. The two trees in Staudt’s proof.
Staudt then gave a beautiful argument proving that any polyhedron meeting these criteria must satisfy the polyhedron formula. We now give a brief sketch of this proof.
Color a vertex of the polyhedron red. Beginning at this vertex, color one of the adjacent edges and its other vertex red (the process is illustrated for a cube in figure 15.8 with the thick, solid lines representing red edges). Then pick one of the two red vertices and color an adjacent edge red, including the opposite vertex. Continue coloring edges and vertices in this way obeying one important condition: never create a red circuit. Eventually this process will end. For any polyhedron satisfying Staudt’s conditions this will occur precisely when all V vertices have been colored red. Because this collection of red edges has no circuit, it is a tree, and as we saw earlier (figure 13.3 and accompanying text), there must be V − 1 red edges.
Now, place a blue vertex inside of each face. Draw a blue edge from one blue vertex to an adjacent blue vertex whenever they are not separated by a red edge (blue edges are dashed lines in figure 15.8). Again, for a polyhedron satisfying Staudt’s criteria, the resulting blue graph will be a tree. This blue tree has F vertices, so it has F − 1 edges. The crucial observation is that every edge in the original polyhedron is either red or is crossed by a blue edge. Thus the number of edges is the sum of the number of red edges and the number blue edges:
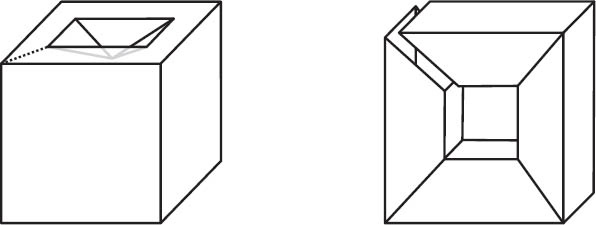
Figure 15.9. Altering an annular face and cutting a torus.
E = (V − 1) + (F − 1),
or rearranging terms, V − E + F = 2.
We should take a moment and revisit the three exceptions of Lhuilier (shown in figure 15.1) and convince ourselves that they are ruled out by Staudt’s definition of polyhedron. Lhuilier’s first polyhedron has an annular face. Because it is impossible to get from the outside edges of the annulus to the inside edges, condition number 1 fails. Notice that it is possible to change this polyhedron so that it complies with Staudt’s definition. To do so, we simply add an artificial edge that connects the inside of the annular face to the outside (as in figure 15.9).
The second polyhedron has a tunnel through its center. This polyhedron fails condition number 2 because, as we see in figure 15.9, it is possible to cut a circuit of edges that does not disconnect the polyhedron. In 1879 R. Hoppe remarked, “Let the polyhedron be made of some stuff that is easy to cut like soft clay, let a thread be pulled through the tunnel and then through the clay. It will not fall apart.”13 Recall that Lhuilier did not give a proper definition of tunnel. Hoppe used the ideas in Staudt’s paper to help rectify this situation. He defined a tunnel in terms of the number of cuts needed to disconnect the surface. We will return to this idea again in chapter 17.
Finally, we can dismiss Lhuilier’s third exception easily. This exception, a polyhedron with a polyhedral cavity, makes sense only for solid polyhedra, and Staudt assumed his polyhedra were hollow. Even if he did allow solid polyhedra, Staudt’s condition number 1 fails since there are no edges from the inner vertices to the outer vertices. Although Hessel’s exceptions satisfy Staudt’s two conditions, he, like most mathematicians, did not consider them polyhedra.
Intuitively, the polyhedra that satisfy Staudt’s criteria are those that are “sphere-like” and have faces with a single polygonal boundary. The polyhedra need not be convex, but they cannot have any tunnels. If they were made of rubber and were inflated, they would inflate to a spherical balloon.
This fruitful dialogue about Eulerian an non-Eulerian polyhedra in the first half of the nineteenth set the stage for the field that would become topology. These ideas were explored further by others, culminating in Poincaré’s marvelous generalization of Euler’s formula at the end of the nineteenth century. We will discuss this development in chapters 17, 22, and 23.


