CHAPTER 23

HENRI POINCARÉ AND THE ASCENDANCE OF TOPOLOGY

The mathematician’s patterns, like the painter’s or the poet’s, must be beautiful; the ideas, like the colors or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in this world for ugly mathematics.
—G. H. Hardy¹

If Euler’s theorems on the bridges of Königsberg and polyhedra mark the birth of topology, and the contributions of Listing, Möbius, Riemann, Klein, and other nineteenth-century mathematicians signify topology’s adolescent years, then its coming of age was signaled by the work of Henri Poincaré. Before this there were theorems that we now categorize as topological, but it was not until the waning years of the nineteenth century that Poincaré systematized the field.

Looking back at his complete body of work, we see a common theme: a topological view of mathematics. Perhaps this qualitative approach to the subject came from his distaste for (or as he said, his difficulty with) performing mathematical calculations. Perhaps it was in response to his notorious lack of artistic talent (remember, he called geometry “the art of reasoning well on badly made figures”). Regardless of the cause, Poincaré eventually recognized this common trait, and wrote, “Every problem I had attacked led me to Analysis Situs.”²

Poincaré was referring to the seminal 123-page article Analysis Situs³ that he wrote in 1895. In the next decade he followed up with five groundbreaking sequels, or complements as he called them.⁴ About these six papers, Jean Dieudonné wrote:

As in so many of his papers he gave free rein to his imaginative powers and his extraordinary “intuition,” which only very seldom led him astray; in almost every section is an original idea. But we should not look for precise definitions, and it is often necessary to guess what he had in mind by interpreting the context. For many results, he simply gave no proof at all, and when he endeavored to write down a proof hardly a single argument does not raise doubts. The paper is really a blueprintfor future developments of entirely new ideas, each of which demanded the creation of a new technique to put it on a sound basis.⁵

One imagines a Johnny Appleseed, wandering through a barren land, scattering seeds that would later grow into fruit-bearing trees. It is hardly an exaggeration to say that nearly all of the research in topology until the early 1930s came from the work of Poincaré.

One of his contemporaries wrote, “In the domain of Analysis Situs Poincaré has recently brought us an abundance of new results, but at the same time raised an abundance of new questions which still await settlement.i⁶ The gaps and holes in Poincaré’s arguments were real, and they took time to sort out. The intuitive approach to the subject by Poincaré and his predecessors needed to be supported by solid mathematical arguments. Rigor and a uniform standard for proof in topology appeared around 1910, and it took several decades to build a solid structure from Poincaré’s blueprints.

One of Poincaré’s many important contributions was his invention of homology.This was an ingenious way of formalizing the study of Riemann’s connectivity numbers and Betti’s higher-dimensional generalizations. Today homology is the primary means of analyzing manifolds. He introduced homology in Analysis Situsand refined it in each of the complements. It took approximately thirty years for the theory of homology to take its modern form.

It is beyond the scope of this book to describe homology theory, either in modern terms or in Poincaré’s. Instead, we will settle for a superficial account with a focus on intuition. Rather than give the n-dimensional version, we will discuss 1-dimensional homology on surfaces.

One way to view 1-dimensional homology is to look at loops drawn on a surface. We will not focus on a fixed loop, but we will let it move around on the surface. It can stretch, shorten, and wiggle as needed, just as long as it does not break or leave the surface.

The simplest possible loop is one that is topologically trivial—one that can be shrunk back to a point. It may zig and zag around the surface wildly, but it does not go around any holes. For instance, because a sphere has no holes, any loop drawn on the surface of the sphere can be shrunk to a point. The simplest surfaces are those for which, like the sphere, every loop is topologically trivial. Such a surface is called simply connected.As we see in figure 23.1, a disk and a sphere are simply connected, but an annulus and a torus are not.

Figure 23.1. A disk and a sphere are simply connected, but an annulus and a torus are not.

Figure 23.2. The cycle c is can be deformed into the cycle a + b.

We know from the classification of surfaces that the sphere is the only simply connected closed surface. All others have infinitely many nontrivial loops. Poincaré realized that it was important to count the essential, or independent, nontrivial loops on the surface. For orientable surfaces, he called this number the 1-dimensional Betti number,in honor of Betti. In order to compute this number, he defined a strange arithmetic on loops, which we write as addition.

In homology, every loop has an orientation and is called a cycle. So the cycles a and −a are the same loop, but with opposite orientations. The sum of two loops a and b is the union of the two cycles, thus a + b and b + a are the same, or with the notation we will use, a + b ≡ b + a. At times we may want to think of a + b as a loop itself. According to our arithmetic we could follow loop a then b or loop b then a. Although these may be different loops, they represent the same cycle. We let two cycles with opposite orientations cancel, so a + (−a) + b − b. Furthermore, if the cycle a can be deformed into the cycle b, then a − b.

To get a feeling for how this addition works, consider the three cycles a, b, and c on the torus in figure 23.2. As we can see, it is possible to deform the cycle c so that it coincides with the cycle a followed by the cycle b. Thus c and a + b are the same cycle, or c ≡ a + b.

Figure 23.3. A zero cycle on the double torus that cannot be shrunk to a point.

If this is truly like addition, there must be a zero cycle. What does a zero cycle look like? The most obvious zero cycle is one that can be shrunk to a point. On a simply connected surface every cycle is zero. Is that it? Are the topologically trivial loops the only zero cycles? They are not. The loop w in figure 23.3 runs around the waist of the double torus and cannot be shrunken to a point. However, we can deform it so that it traces out the cycle u, then u, then −u, then −v. So, w ≡ u + v + (−u) + (−v) ≡ 0.

We see that the cycle c in figure 23.2 can be written as a sum of cycles a and b. It turns out that any cycle on the torus can be written as a sum of a and b. In other words, given any cycle d on the torus, it is possible to find integers m and n so that d ≡ ma + nb. In essence, a and b are the only cycles that matter, so, according to Poincaré, the 1-dimensional Betti number of the torus is 2. Likewise, for the double torus in figure 23.3 the loops u and v are essential, and there are two more around the other handle. The 1-dimensional Betti number of the double torus is 4.

For orientable surfaces the number of such loops is the first Betti number, but for nonorientable surfaces, something strange happens. In our experience, if we saw the equation a + a = 0, then we would conclude that a = 0. This is always the case for real numbers. However, for cycles it may be the case that a 0, but a + a ≡ 0. In fact, this is not so foreign to us. Many cars have odometers that go up to 99,999 miles. According to such an odometer, 50, 000 + 50, 000 = O. Another example is a clock running on military time. Midnight is 0:00, noon is 12:00, and immediately before midnight is 23:59. So, 12 hours after 12:00 is 0:00, or 12 + 12 = 0.

Figure 23.4. For the projective plane, 2a ≡ 0.

To see this strange arithmetic in action we return to the projective plane and the Klein bottle. We saw in figure 22.8 that the connectivity number of the projective plane is 1. Let us denote the corresponding cycle by a and give it an orientation as in figure 23.4. Now a + a, or 2a for short, is the cycle tracing out a two times. Remarkably, as we can see in the figure, this doubled cycle is indeed topologically trivial—by manipulating the loop it is possible to shrink it to a point. So 2a ≡ 0.

The same thing occurs on the Klein bottle, but the rationale is slightly different. Earlier we saw that the connectivity number of the Klein bottle is 2. Denote the corresponding cycles (with orientation) b and c, as in figure 23.5. As we can see, the doubled cycle 2b is equivalent to b + c + (−b) + (−c). In other words, even though 2b is not topologically trivial, 2b ≡ 0.

So we may separate these essential cycles into two classes, depending on whether or not they exhibit this behavior. We continue to call the number of cycles that do not have this behavior the 1-dimensional Betti number. If the surface has a cycle a for which na ≡ 0 (and n is the smallest positive for which this is true), then we call n a torsion coefficient for the surface. Thus, in dimension 1 the projective plane has Betti number 0 and a torsion coefficient of 2, while the Klein bottle has Betti number 1 and torsion coefficient 2.

In a similar manner Poincaré defined the higher-dimensional Betti numbers and torsion coefficients, except that instead of having loops as cycles he used higher-dimensional manifolds. Poincaré proved that both the Betti numbers and the torsion coefficients are topological invariants for manifolds. In table 23.1 we show the Betti numbers and torsion coefficients for closed surfaces. We let b_i denote the i th Betti number.*

Figure 23.5. For the Klein bottle, 2b ≡ b + c + (−b) + (−c) − 0.

TABLE 23.1:
Betti numbers and torsion coefficients of surfaces.

In Analysis Situs Poincaré followed the ideas of Riemann and Betti. In response to a call for rigor, he changed directions in his later papers. It was at this point that he began working with simplicial complexes, the n-dimensional generalization of polyhedra. In this context, the cycles in homology were built from the features on the polyhedron. For example, a 1-dimensional cycle was not an arbitrary loop on the manifold, but sequences of edges on the polyhedron that formed a loop.

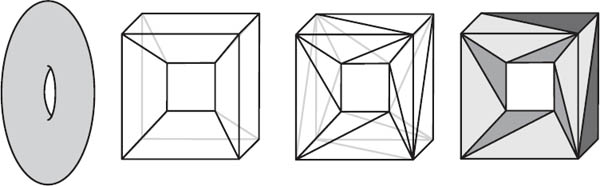
Figure 23.6. A simplicial complex for a solid torus.

On a practical level, simplicial complexes are much easier to work with than Poincaré’s first model. Poincaré could describe the complex in terms of an incidence matrix, a rectangular array of numbers that showed which simplices were neighbors. Using these matrices, it was purely a mechanical process to compute Betti numbers and torsion coefficients.

With this higher-dimensional generalization of a polyhedron, it is natural to ask whether the Euler number can be extended to higher-dimensional manifolds. Indeed, as Cauchy and Schläfli did before him, Poincaré generalized the Euler number by computing the alternating sum of the number of k-simplices. In other words, if a manifold M can be partitioned as a simplicial complex with a_k simplices of dimension k, then he defined the Euler number to be

_X(M) = a₀ − a₁ + a₂ − . . . ± a_n.

This generalization of the Euler number (or Euler characteristic) to n-dimensional space is called the Euler-Poincaré characteristic of M.

For example, a solid torus is a 3-manifold with boundary (the boundary is the torus, a 2-manifold). In figure 23.6 we show how to partition the solid torus as a simplicial complex. It has 12 vertices (0-simplices), 36 edges (1-simplices), 36 faces (2-simplices), and 12 triangular pyramids (3-simplices). So, a₀ = 12, a₁ = 36, a₂ = 36, and a₃ = 12, and the Euler-Poincaré characteristic is _X(solid torus) = 12 − 36 + 36 − 12 = 0.

Just as the Euler number is a topological invariant for surfaces, so is the Euler-Poincaré characteristic an invariant for n-manifolds. To prove this, Poincaré showed something much more interesting. He proved that if the kth Betti number is b_k, then

TABLE 23.2:
The symmetry of Betti numbers.

^X(M) = b₀ − b₁ + b₂ − . . . ±b_n.

That is, to compute the Euler-Poincaré characteristic, we throw out the torsion coefficients and take the alternating sum of the Betti numbers! In table 23.1 we can see that this equality holds for the Betti numbers for surfaces. Because each of the b_k are topological invariants, so is the alternating sum. So the Euler-Poincaré characteristic is a topological invariant.

In 1895 Poincaré discovered a beautifully symmetric relation among the Betti numbers.⁷ The sequence of Betti numbers for several manifolds are shown in table 23.2. He noticed that the Betti numbers came in pairs, with the first Betti numbers the same as the last ones: b₀ = b_n, b₁ = b_n−1, etc. This became the celebrated Poincaré duality theorem.

We encountered duality earlier when we discussed Kepler’s pairing of the Platonic solids (chapter 6). The use of the term “duality” in both cases is not a coincidence; Kepler’s observation is Poincaré duality in disguise. Poincaré duality states that when computing Betti numbers for a manifold, we are free to exchange the roles of i-dimensional and (n − i)-dimensional simplices. The duality of the Platonic solids illustrates this behavior. For instance, the icosahedron gives a partition of the sphere into vertices, edges, and faces. When we use Kepler’s notion of duality to turn every vertex of the icosahedron into a face and every face into a vertex, we get the dodecahedron, another partition of the sphere.

Figure 23.7. The 3-torus and a nonorientable 3-manifold.

In Analysis Situs Poincaré wrote, “This theorem has not, I believe, ever been stated; it is, however, known to many, who have even found some applications of it.”⁸ We do not know who these other people were nor how they used the relationship, but Poincaré’s primary use was to prove the surprising fact that the Euler-Poincaré characteristic of any closed orientable manifold of odd-dimension is zero!

Indeed, consider the 3-torus, the 3-manifold obtained by gluing together the sides of the left-hand cube in figure 23.7. It has Betti numbers b₀ = 1, b₁ = 3, b₂ = 3, and b₃ = 1 (we will not prove this), so the Euler-Poincaré characteristic is,

χ(3-torus) = 1 − 3 + 3 − 1 = 0.

In general, suppose M is any closed orientable manifold of odd dimension n. Poincaré duality and the alternating sum of the Euler-Poincaré characteristic give us pairings of equal Betti numbers with opposite signs. They cancel to give zero:

It turns out that the Euler-Poincaré characteristic of any nonorientable closed manifold of odd dimension is also zero. We omit the complicated justification, but we will illustrate with an example. The 3-manifold obtained by gluing together the sides of the right-hand cube in figure 23.7 is nonorientable. It has Betti numbers b₀ = 1, b₁ = 2, b₂ = 1, and b₃ = 0 (it also has torsion in dimensions 1 and 2). We can see that Poincaré duality does not hold, yet the Euler-Poincaré characteristic is still zero:

χ(M) = 1 − 2 + 1 − 0 = 0.

We should point out that odd-dimensional manifolds with boundary need not have zero Euler-Poincaré characteristic. For instance, the Euler- Poincaré characteristic of the n-dimensional ball, Bⁿ, is 1 for all n.

It was during the first three decades of the twentieth century that topology made the transition from a discipline built on intuitive arguments to one based on rigorous proof. That is to say, it was during this time that topologists removed the gaps, holes, unwarranted assumptions, and errors from Poincaré’s brilliant work.

For example, consider the following two assumptions made by Poincaré. First, he asserted that every manifold could be expressed as a simplicial complex, or more concisely, that every manifold can be triangulated. Second, he assumed that the Hauptvermutung held for arbitrary manifolds. (Recall that the Hauptvermutung says that any two partitions of a manifold can be refined by adding simplices so that they are topologically the same.) It turns out that in general, neither of these assumptions is true for general manifolds. Yet later mathematicians showed that Poincaré’s conclusions still hold.

A significant improvement to Poincaré’s ideas was made by the German mathematician Emmy Noether (1882–1935). Noether, the daughter of a mathematician, is remarkable for the prejudices she was forced to overcome. She was a woman in a highly male-dominated field. In 1904 the University of Erlangen permitted women to enroll, but until then she was only able to audit classes. She completed her PhD in 1907. In 1915, after her reputation as a first-class research mathematician began to spread, Klein and David Hilbert (1862–1943) brought her to Göttingen, intent on having her on the faculty. But it was not until 1919 that she was permitted to hold this position; in the meantime her courses were advertised under Hilbert’s name, with her listed as an assistant. When the Nazis came to power, life changed for many Germans. In 1933 the Jewish Noether was forced to leave Göttingen for Bryn Mawr College in the United States. She died two years later.

She is most well-known for her pioneering work in the field of abstract algebra. Broadly speaking, abstract algebra is the study of sets with one or more binary operations (such as addition and multiplication and their inverses, subtraction and division).

Figure 23.8. Emmy Noether.

Until the middle of the 1920s homology was described in terms of Betti numbers and torsion coefficients. It took the algebraist Noether to recognize that there was significantly more structure to homology. She discerned that the key feature in homology was the ability to add and subtract cycles. Focusing on this arithmetic, she observed that homology was a specific instance of an algebraic entity called a group, and that Betti groups, or homology groups as they are now called, were the right way to view homology. In his autobiography, Pavel Aleksandrov wrote, “I remember a dinner at Brouwer’s in [Noether’s] honour during which she explained the definition of the Betti groups of complexes, which spread around quickly and completely transformed the whole of topology.”⁹

Suddenly topologists had a brand-new tool kit available to them. All of the techniques and theorems from group theory were at their disposal. Powerful theorems could be proved without reinventing the wheel. Betti numbers and torsion coefficients fell out of the machinery in an obvious way, and the invariance of the Euler-Poincaré characteristic became a simple proof. In Aleksandrov’s memorial address for Noether, he wrote:

These days it would never occur to anyone to construct combinatorial topology in any way other than through the theory of . . . groups; it is thus all the more fitting that it was Emmy Noether who first had the idea of such a construction. At the same time she noticed how simple and transparent the proof of the Euler-Poincaré formula becomes if one makes systematic use of the concept of Betti group.¹⁰

Yet again we see the power that results from the merging of different branches of mathematics. Descartes used analysis to understand geometry. Riemann and Poincaré used topology to understand analysis. Gauss and Bonnet used topology to understand geometry. Now topologists are free to use algebra to understand topology. This cross-fertilization has been extremely fruitful.

The incorporation of algebra into topology is so important that this entire area of topology—virtually all of the topology we have discussed in this book—is now called algebraic topology. In the decades after Poincaré’s work, algebraic topology expanded beyond homology groups to include many other algebraic structures. Today, most topologists are algebraic topologists.

* Poincaré followed Riemann’s convention and took the ith Betti number to be one larger than this value, but for simplicity we will use the modern convention