CHAPTER 6
KEPLER’S POLYHEDRAL UNIVERSE
During the period of Arabic mathematics, Europe was experiencing the darkness of the Middle Ages. Very few Europeans received a formal education; the great works of classical antiquity were all but forgotten; mathematical scholarship was almost nonexistent. Only the minimal teaching of geometry and arithmetic remained in monastic schools. For hundreds of years there were virtually no significant contributions made to the body of mathematics.
It was not until the European Renaissance in the fifteenth century that mathematical activity began to reemerge. The rise of the humanist movement brought a renewed interest in the Greek classics—first Greek literature, then Greek mathematics. The romance of Greek intellectual life is beautifully depicted in Raphael’s fresco School of Athens (1510–1511), which features an imaginary gathering of Pythagoras, Euclid, Socrates, Aristotle, Plato, and other Greek scholars (figure 6.1).
Perspective was a prominent feature in Renaissance artwork. Polyhedra and the skeletons of polyhedra were excellent subjects for demonstrating an artist’s mastery of perspective. Artists such as Piero della Francesca, Albrecht Dürer, and Daniele Barbaro contributed to both mathematics and art in their writings about perspective in polyhedra. Among the many artists who featured polyhedra in their artwork (see figures 6.2 and 6.3) are Leonardo da Vinci, who illustrated Fra Luca Pacioli’s book De divina proportione (1509); Wentzel Jamnitzer, who created intricate and elaborate engravings of real and impossible polyhedra; Jacopo de Barbari, who painted a portrait of Luca Pacioli with his polyhedra; Paolo Uccello, who included polyhedra in his paintings and in the mosaics that he lay in the floor of the San Marco Basilica in Venice; Fra Giovanni da Verona, who created beautiful intarsia (wooden mosaics); and, as we will see (figures 6.5 to 6.8), Johannes Kepler, the physicist and mathematician.

Figure 6.1. Raphael’s School of Athens (Fresco in the Apostotic Palace in the Vatican).
Like the Renaissance scholars and artists of the two centuries preceding him, Kepler was fascinated by polyhedra. Today Kepler is most well known as an astronomer, famous for his three laws of planetary motion (describing the elliptical motion of the planets about the sun), but he made many other contributions to science and mathematics. He used the ideas of the infinite and the infinitesimally small in a way that anticipated calculus. He published work in the field of optics. He was an early user of logarithms. And Kepler made contributions, both real and fanciful to the theory of polyhedra.
Kepler was born December 27, 1571, in the small town of Weil der Stadt, Württemburg, in the Holy Roman Empire in present-day Germany. He had an extraordinarily difficult life: he was a sickly child raised in a troubled household, he endured religious persecution, his first wife and his favorite son died of smallpox, his mother was charged with witchcraft, and he died at the age of 58 while on a journey to recover his back salary. Despite these hardships, Kepler was a deeply religious man. He was headed for a career as a Lutheran minister until, at the age of twenty-three, he left the seminary to take a teaching position in mathematics and astronomy. His religious beliefs were important to him and, as can be seen in his writing, they often served as inspiration for his scientific work. As one of Kepler’s biographers, Arthur Koestler, wrote, “This coexistence of the mystical and the empirical, of wild flights of thought and dogged, painstaking research, remained . . . the main characteristic of Kepler from his early youth to his old age.”2

Figure 6.2. Leonardo da Vinci’s truncated icosahedron and pentakis dodecahedron from De Divina Proportione.
Kepler believed that God created a world with mathematical beauty. Surely, Kepler believed, the existence of only five regular polyhedra must be significant; surely they must be reflected in the composition of the universe. Koestler wrote, “For Kepler’s misguided belief in the five perfect bodies was not a passing fancy, but remained with him, in a modified version, to the end of his life, showing all the symptoms of a paranoid delusion; and yet it functioned as the vigor motrix, the spur of his immortal achievements.”3
Figure 6.3. A marble inlay by Uccello (top left), one of Fra Giovanni’s intarsia (top right), and samples from Wentzel Jamnitzer’s Perspectiva corporum regularium (1568).
Figure 6.4. Johannes Kepler.
The inspiration for Kepler’s first model of the solar system came on July 9, 1595, while he was lecturing to a room full of students. At this time the geocentric (Earth-centered) Ptolemaic view of the solar system was generally held to be the correct model. A half-century earlier Nicolaus Copernicus (1473–1543) had argued for the heliocentric (Sun-centered) model, but at this point, for various reasons, the heliocentric model was rejected by most intellectuals.
One day, as Kepler drew polygons inscribed in circles, he had the inspiration that this might be the secret to the planetary orbits: perhaps the orbits of the planets were nested circles inscribed in various polygons, with the sun at the center. After spending a summer meticulously working through the details, he realized that this was not the correct model for the solar system. Instead of abandoning this model entirely, he revised it and created one with which he was much happier. His new model appeared in his first book, Mysterium Cosmographicum (Cosmic Mystery) in 1596.4
Kepler had realized that polygons and circles were not the right objects for a model of the solar system; he shifted his attention up one dimension to polyhedra and spheres. He argued that the existence of the five Platonic solids must be related to the existence of the six known planets: Saturn, Jupiter, Mars, Earth, Venus, and Mercury. He claimed that the orbits of the planets are related to the nesting of the five Platonic solids inside spheres.
Take the sphere containing the orbit of the most distant planet, Saturn, along its equator. Inside this sphere inscribe a cube, and then, inside the cube, inscribe another sphere. Along the equator of this sphere, Kepler contended, is the orbit of Jupiter (see figure 6.5). Continuing on in this manner (tetrahedron, sphere, dodecahedron, sphere, icosahedron, sphere, octahedron, sphere), we find the orbits of all six planets. Kepler wrote:

Figure 6.5. Kepler’s early view of the solar system (from Cosmic Mystery).
This was the occasion and success of my labors. And how intense was my pleasure from this discovery can never be expressed in words. I no longer regretted the time wasted. Day and night I was consumed by the computing, to see whether this idea would agree with the Copernican orbits, or if my joy would be carried away by the wind. Within a few days everything worked, and I watched as one body after another fit precisely into its place among the planets.5
Thus, Kepler was the first professional astronomer to come out publicly, in print, in support of the Copernican model. At this time even Galileo (1564–1642), six years Kepler’s senior, was silent in this matter.
The first half of Cosmic Mystery was very mystical—Kepler indulged in astrology, numerology, and symbology. He gave elaborate nonscientific reasons for why his model of the solar system was correct. He saw a very distinct hierarchy among the Platonic solids. For example, they were divided into the primaries (the tetrahedron, the cube, and the dodecahedron) and secondaries (the octahedron and the icosahedron), the primaries being those with three faces meeting at each vertex. He asserted that “containing is . . . more perfect” than being contained,6 and in his planetary model the primaries were the outer polyhedra and the secondaries the inner, with earth’s orbit situated between the two classes.
Then, abruptly, in the second half of the book he switched to a scientific argument, complete with astronomical data. In order for his theory and the data to agree he made a few modifications to the model. Although he did not yet know that the orbits of the planets were ellipses, he knew that they were not circular. So, to contain the planets, each sphere in the model had to have some thickness; as a planet orbited in its noncircular pattern it remained inside its spherical shell. Kepler’s model is surprisingly accurate; however, he realized that the data still did not quite fit the model (especially the orbits of Jupiter and Mercury). As a result, he found various ways to explain away these discrepancies, such as discrediting the data that he was using (which had come from Copernicus).
Later, Kepler himself proved that this archetype for the solar system was wrong. He wrote, “I indeed confess that the head of astronomy is struck off.”7 By sifting though a huge amount of data on Mars’s orbit that were left to him by the astronomer Tycho Brahe (1546–1601), Kepler deduced the true motion of the planets. In one of the great feats in the history of science, he used these data to discover his three laws of planetary motion (the first two in 1609, the third in 1619). Thirty years after his death, these laws were mathematically verified by Isaac Newton. Despite the false claims in Cosmic Mystery, it is interesting that many of these outrageous ideas contain a grain of truth. Some of Kepler’s greatest scientific accomplishments can be traced back to the seemingly nonsensical ideas in this book.
Kepler’s most significant contribution to the theory of polyhedra came near the end of his career in his 1619 work Harmonice mundi (The Harmony of the World.)8 This treatise has five parts; the first two are devoted to mathematics. In them Kepler discussed regular and semiregular polyhedra. He rediscovered all thirteen Archimedean solids and proved that there are no others. He presented the class of polyhedra called antiprisms. He also found a pair of star polyhedra, known today as the small and the great stellated dodecahedra (see figure 6.6). He called a polyhedron of this type an echinus, which means hedgehog or sea urchin. Later we will return to these star polyhedra and see how they can be viewed as regular polyhedra and cause trouble for Euler’s formula.
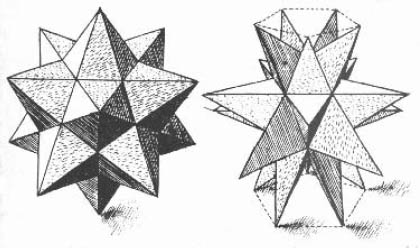
Figure 6.6. Kepler’s drawings of the star polyhedra (from The Harmony of the World).
Even this late in his career, Kepler was fascinated by the Platonic solids. He subscribed to the Greek theory that there were four elements and to Plato’s theory that they were made from the Platonic solids. We must remember that the publication of The Harmony of the World was still forty-two years before Boyle’s revolutionary text, The Sceptical Chymist. In The Harmony of the World Kepler used ideas of Plato and Aristotle together with his own unscientific arguments to justify that the four elements were Platonic solids.
He argued that because a cube can be placed flat on a table in a way that it is not easily displaced, it is the most stable of the Platonic solids; thus it must be earth. An octahedron, held between two fingers, can be spun easily; thus it is the most unstable, and must be air. The tetrahedron contains the least volume for a fixed surface area; thus it is the driest of the five and must be fire. Similarly, the icosahedron contains the largest volume for a fixed surface area; so it is the wettest, and must be water. Kepler saw a relationship among the twelve faces of the dodecahedron and the twelve signs of the Greek Zodiac; because of this relationship, he argued that the dodecahedron must represent the universe. The correspondence between these elements and the Platonic solids can be seen in Kepler’s famous illustration in figure 6.7.
In The Harmony of the World, we see again the dichotomy between Kepler’s mystical tendencies and his brilliant scientific thought. In this work he made erroneous claims about atomic theory, but he also made an important new observation about the Platonic solids. He noticed that there is an antisymmetric relationship between the octahedron and the cube; an antisymmetric relationship between the dodecahedron and the icosahedron; and a self-symmetric relationship for the tetrahedron. As we can see in table 6.1, the cube and the octahedron both have 12 edges. The number of faces on the cube (6) is equal to the number of vertices on the octahedron, and the number of vertices on the cube (8) is equal to the number of faces on the octahedron. The same mirroring relationship holds for the icosahedron and the dodecahedron—both polyhedra have 30 edges, there are 20 faces on the icosahedron and 20 vertices on the dodecahedron, and there are 12 vertices on the icosahedron and 12 faces on the dodecahedron. The tetrahedron does not pair up with another regular polyhedron, but it has the same number of faces as vertices, so it pairs with itself.

Figure 6.7. Kepler’s drawings of the Platonic solids (from The Harmony of the World).
TABLE 6.1:
The number of vertices, edges, and faces in the Platonic solids.

Kepler recognized that this antisymmetry had a physical interpretation. Take one of the regular polyhedra, the cube, for instance. Place a new vertex at the center of each face. These eight points form the vertices of an octahedron. This new polyhedron is called the dual of the original polyhedron. In figure 6.8 we see Kepler’s illustration that the octahedron is the dual of the cube. Notice that each face of the cube corresponds to a vertex of the octahedron, so the number of faces of a cube is equal to the number of vertices of an octahedron. Examining the figures more closely, we see that each edge of the octahedron can be paired with an edge of the cube that is oriented at a right angle to it; thus both polyhedra must have the same number of edges. Moreover, each vertex of the cube corresponds to a face of the octahedron, and consequently there must be the same number of each. In this way we find the mirroring relationship present in table 6.1.
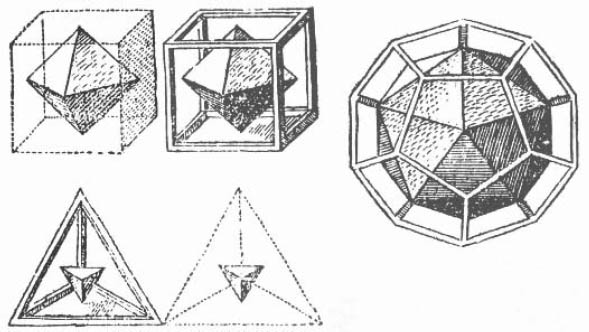
Figure 6.8. Kepler’s depiction of dual polyhedra (from The Harmony of The World).
Similarly, Kepler showed that the icosahedron is the dual of the dodecahedron and that the tetrahedron is its own dual (see figure 6.8). Although Kepler knew that duality was reciprocal (the cube can be inscribed in the octahedron and the dodecahedron in the icosahedron), he did not show this. It did not fit with his hierarchy. Because he believed that containing was more perfect than being contained, he showed only primaries containing secondaries.
As was his style, Kepler could not resist sharing his unique interpretation of this mathematical observation. He assigned genders to the solids and used duality to indicate sexual compatibility. The cube and the dodecahedron (both dominant primaries) were male and contained the female octahedron and icosahedron (secondaries). The tetrahedron was a hermaphrodite because it contained itself. The faces and vertices were the sexual characteristics because that was where the solids met. Kepler wrote:
However, there are two notable marriages, so to speak, of these figures, by combination from the two classes: the males, the cube and the dodecahedron from the primaries, the females, the octahedron and the icosahedron from the secondaries. In addition to these there is one which is, so to speak, celibate or hermaphrodite, the tetrahedron, because it is inscribed in itself, just as the feminine ones are inscribed in, and so to speak subject to, the males, and have the female tokens of their sex opposite to the masculine ones, or in other words the angles to the plane faces.9

Figure 6.9. Round dice.
Toy makers have creatively used the properties of regular and non- regular polyhedra to make many varieties of exotic dice. One ingenious toy maker has even used the duality of the regular polyhedra to make fair, usable round dice! The pips are painted on the surface of the sphere as if it was a cube (see figure 6.9). On the inside is a cavity in the shape of the cube’s dual—an octahedron. A heavy ball bearing rattles around inside the octahedron until it comes to rest at one of its vertices. The weight of the ball bearing forces one of the die’s “faces” to come to rest at the top of the die.
It is possible to extend the notion of duality to polyhedra that are not regular, although the definition is slightly more involved. Duality is a powerful, recurrent theme in mathematics. It is often the case that we create dual pairs by reversing some key quantity. For polyhedra, we are reversing dimension: zero-dimensional vertices replace 2-dimensional faces, and 2-dimensional faces replace zero-dimensional vertices. In other situations duality is obtained by reversing other quantities such as up and down, positive and negative, and so on. Sometimes the object that is most similar to a given object is the one that is its exact opposite. We will return to the notion of duality in chapter 23.
By the seventeenth century mathematics had become an active academic discipline in Europe. The long dry spell had ended. Polyhedra, reintroduced by the artist community, was again a subject of mathematical investigation. As we see in chapter 9, in approximately 1630 Descartes discovered important properties of polyhedra, but the world would not learn of this until 1860. The first major contribution to the theory of polyhedra in two thousand years would have to wait another century for Euler’s brilliant insight.


