CHAPTER 17
ARE THEY THE SAME, OR ARE THEY DIFFERENT?
One of the most important recurring questions in mathematics is: are the two mathematical objects X and Y the same? In different contexts we have different criteria for what “the same” means. Often, when we say the same we mean equal, such as the expression 5 · 4 + 6 − 23 and the number 18, or the polynomials x2 + 3x + 2 and (x + 2)(x + 1). In other circumstances the same may not mean equal. For a sailor navigating by compass, two angles are the same if they differ by 360° (30° is the same as 390°). A geometer may say that two triangles are the same if they are congruent or perhaps if they are similar.
In topology we have a looser set of criteria for sameness than we do in geometry. This is where the rubber-sheet analogy comes into play. Intuitively, if one shape can be continuously deformed into the other, then they are the same. Bending, twisting, stretching, and squashing the shape does not change its topology. For example, the circle shown in figure 17.1 is the same as the tangle to its right. On the other hand, puncturing a shape, cutting it, or gluing it to itself will likely yield a shape that is topologically different. A circle is not the same as a circle glued to itself in the form of a figure eight.
In the first half of the nineteenth century mathematicians struggled to classify those polyhedra that satisfy Euler’s formula—the so-called Eulerian polyhedra. We came to the vague understanding that all polyhedra that are “sphere-like” are Eulerian, whereas the bizarre exceptions of Lhuilier and Hessel are not. It turns out that Euler’s formula applies to any polyhedron that is topologically the same as a sphere. A cube, any Platonic or Archimedean solid, and even certain nonconvex polyhedra can be deformed into a round, spherical ball (see figure 17.2). Non-Eulerian polyhedra, such as one formed by joining two polyhedra along an edge or one shaped like a torus, are not topologically the same as a sphere.
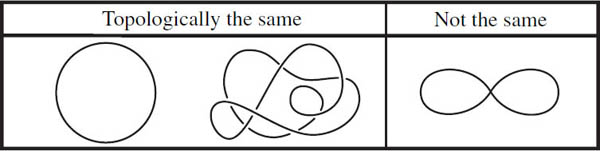
Figure 17.1. The tangle is topologically the same as a circle, but the figure eight is not.
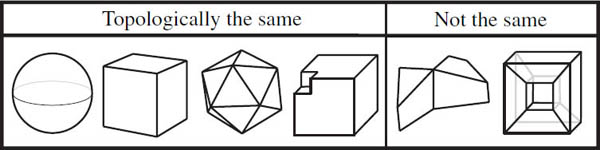
Figure 17.2. Polyhedra that are topologically the same as and different from a sphere.
It may seem that this study of shapes is intuitive, but it is remarkable how often we stumble upon counterintuitive results. For instance, in figure 17.3 we begin with a double torus hanging on a clothesline with the string passing through one of the holes. By topological manipulations (and no cutting or gluing!) we achieve what may at first appear to be an impossibility—we transform it into a double torus hanging on a clothesline through both holes.
In chapter 16 we saw the difference between extrinsic and intrinsic dimension. We could use similar terminology in this context as well. The examples shown earlier in this chapter have what we might call the same extrinsic topology because one shape can be deformed into the other in 3-dimensional space. Mathematicians call two shapes with the same extrinsic topology isotopic. Isotopic is a valid choice for the definition of topologically “the same,” but it turns out that topologists want more freedom. We need a less restrictive definition for “the same.”
Figure 17.3. The double-torus clothesline trick.
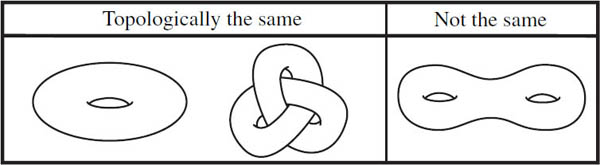
Figure 17.4. Shapes that are topologically the same as and different from a torus.
For two shapes to be topologically the same, they must have the same intrinsic topology. If two surfaces are the same, then regardless how clever an ant living on the surface is, she will not be able to tell one from the other without leaving the surface. It is possible to find two surfaces that are the same, but for which one cannot be deformed into the other. Thus the rubber sheet analogy is not a perfect one.
To understand this new definition, we must revisit our cutting and gluing policy. While it is true that cutting and gluing usually change the topology of a surface, this is not always the case. An important exception is: cutting a shape, then gluing the severed pieces so that the cuts line up exactly as they did before. In this case the topology does not change. If we cut a torus around the tube to form a cylinder, tie the cylinder into a knot, and then reglue it (as in figure 17.4), the resulting shape is still topologically the same as a torus. Notice that this knotted torus cannot be obtained from the original torus simply through deformations in 3-dimensional space—they are not isotopic. The intrinsic topology is the same, but the extrinsic topology is not. On the other hand, there is no way to cut, deform, and reglue a torus to obtain a double torus. A sufficiently clever ant will be able to prove that they are topologically different (and we will see how very soon).
Figure 17.5. A band with two half-twists, but not a band with a single half-twist, is homeomorphic to a cylinder.
Because it is outside the scope of this book, we omit the topologist’s precise definition of “the same.” In essence, two topological objects are the same if there is a one-to-one correspondence between the points in the two objects that preserves closeness—nearby points in one shape correspond to nearby points in the other. This notion of “the same” was introduced by Möbius, who called the correspondence an “elementary relationship.”2 Today such a correspondence is called a homeomorphism. Thus, in the lingo of the topologists, two shapes are the same whenever they are homeomorphic.
Consider the three loops of cloth from the Afghan bands magic trick in chapter 16. One has no twist, one has a single half-twist, and one has two half-twists. Clearly none have the same extrinsic topology. However, according to our rule of thumb, the third shape is homeomorphic to the untwisted cylindrical band, for if we cut the cylinder and gave two half-twists, the cut edges would line up correctly to be reglued (figure 17.5). We will call this third shape a twisted cylinder. This is not the case for the Möbius band. If we cut the cylinder and gave it a half-twist, the cut edges would not line up correctly. Similarly, despite the superficial resemblance between a Möbius band and a twisted cylinder, they are not homeomorphic.
Although our intuition tells us that the Möbius band is not homeomorphic to the cylinder (twisted or not), we have not given a proof. Although it seems unlikely, perhaps there is an elaborate cutting scheme that would turn one into the other. As we learned from the double-torus clothesline trick, we cannot always rely on our gut feeling, but in this case our intuition is correct—they are not homeomorphic.
A topological invariant is a property or mathematical entity associated with a surface that depends only on the topology of the surface. A topological invariant may take the form of a number, such as the number of boundary components. If two surfaces are homeomorphic, then they must have the same number of boundaries. In practice, the contrapositive is more useful: if two surfaces have a different number of boundaries, then they cannot be topologically the same. Because a cylinder has two boundary components and a Möbius band has one, they are not homeomorphic.
Intrinsic dimension is another topological invariant: it allows us to distinguish a (2-dimensional) sphere from a (1-dimensional) circle. We will discuss the notion of dimension more thoroughly in chapter 22.
Orientability is another topological invariant, or more specifically, a topological property. Two surfaces that are topologically the same are both orientable or both nonorientable. Said another way, if one surface is orientable and another is not, then they must not be homeomorphic. It is not difficult to see that a cylinder and a twisted cylinder are both orientable, but a Möbius band is not.
According to our cutting and gluing rules, a strip of paper glued together with an even number of half-twists is topologically the same as a cylinder and one glued with an odd number of half-twists is the same as a Möbius band. The strips with an even number of half-twists are orientable and have two boundary components, while those with an odd number of half-twists are nonorientable and have one boundary, and thus the strips are not homeomorphic to each other. Notice, by the way, that each twisted band has a mirror twin. When it comes time to twist and glue, there are two choices for twisting, a right-hand twist or a left-hand twist.
Orientablility, dimension, and the number of boundary components are three important topological invariants. Another topological invariant, arguably the most important one, is the quantity V − E + F. Given a surface S partitioned into V vertices, E edges, and F faces (of course, we still need to avoid ring-shaped faces), we define the Euler number of S to be V − E + F (the Euler number is often called the Euler characteristic). It is customary to use the Greek letter chi to denote the Euler number, so χ(S) = V − E + F.
The Euler number is a topological invariant for surfaces.
Figure 17.6. Partitions of the sphere, the torus, and the Klein bottle.
By saying that the Euler number is a topological invariant, we mean that each surface has its own Euler’s formula. For example, the sphere in figure 17.6 has 62 vertices, 132 edges, and 72 faces, so its Euler number is
χ(sphere) = 62 − 132 + 72 = 2.
As we know, this is true for any partition of a sphere or anything homeomorphic to a sphere.
The torus in figure 17.6 has 8 vertices, 16 edges, and 8 faces, so its Euler number is
χ(torus) = 8 − 16 + 8 = 0.
Likewise, the Klein bottle in figure 17.6 has 8 vertices, 16 edges, and 8 faces, so
χ(Klein bottle) = 8 − 16 + 8 = 0.
There are several steps involved in proving that the Euler number is a topological invariant. First we must show that any surface can be partitioned into finitely many vertices, edges, and faces. That is, there is no surface that is so bizarre that it has no finite partition (here is where we use the compactness assumption discussed in chapter 16—the Euclidean plane and the open unit disk have no finite partition, and are excluded). When we were working with polyhedra, we were given the partition—it was simply the vertices, edges, and faces of the polyhedron. A surface does not have a built-in partition. Surprisingly, it was not until 1924 that the first proof appeared that is it possible to partition every surface into vertices, edges, and faces.3
Next we must argue that the Euler number is independent of the choice of partition. It is not difficult to see that adding vertices and edges to a partition will not change V − E + F. So we ask, given two partitions of a surface, P and P′, is it possible to add vertices and edges to P and P′ so that the two partitions have the same number of vertices, edges, triangular faces, square faces, pentagonal faces, and so on, and that their placement relative to each other is the same? This problem was recognized early and was nicknamed the Hauptvermutung, which is a short for “the main conjecture of combinatorial topology.” Its proof came late—not until 19434—and as we will see in chapter 23, things are not so nice in higher dimensions. Because the Hauptvermutung is true for every surface, the Euler number is independent of the choice of partition.
Finally, we must show that two homeomorphic surfaces have the same Euler number. If S and S′ are homeomorphic surfaces and P is a partition of S, then because the homeomorphism gives a one-to-one correspondence between S and S′, we may use the homeomorphism to transfer the partition P over to a partition of S′. Clearly, then, χ(S) = χ(S′). Thus, we have completed the sketch of the proof of our theorem—that the Euler number is a topological invariant.
One of the biggest challenges in the study of Euler’s formula for polyhedra was to understand the effect of “tunnels” on V − E + F. Lhuilier and Hessel both asserted that if a polyhedron had g tunnels, then V − E + F = 2 − 2g. Using our modern terminology, they asserted that the Euler number is 2 − 2g. The problem was that they did not define tunnel. Instead of tunnels, we now use handles (in the sense of chapter 16) to describe these topological features. It is interesting that they focused on the holes in the figures, and we now focus on the handles that bound these holes.
Let us examine the effect on the Euler number of adding a handle to a sphere. We must remove two disks from the sphere so that we can attach the handles in their place. We may as well take these two disks to be triangular faces (see figure 17.7). If the partition does not have triangular faces, subdivide a face into triangles. We know that the Euler number of the sphere is 2, and the handle is a cylinder, which has Euler number 0 (the simplest partition has V = 2, E = 3, and F = 1). So, before any cutting and gluing, we have
V − E + F = χ(sphere) + χ(handle) = 2 + 0 = 2.
When we cut away the two triangles we lose two faces. When we glue the handle to the sphere, six pairs of edges are joined. Thus those twelve edges become six edges. Similarly, the twelve vertices become six vertices. After cutting and gluing, V and E both decrease by six and F decreases by two, so V − E + F decreases by two. So,
V − E + F = χ(sphere) + χ(handle) − 2 = 2 − 2 = 0.
Figure 17.7. Adding a handle and a cross cap to a sphere.
Of course, we know that a sphere with a handle is a torus, so this is not surprising.
By the same reasoning, each time we add a handle to a surface, the Euler number decreases by 2. Thus we have a proof of Lhuilier’s observation:
χ(sphere with g handles) = 2 − 2g.
Likewise, we can compute the effect of adding a cross cap. Notice that χ(cross cap) = χ(Möbius band) = 0 (like a cylinder we can have V = 2, E = 3, and F = 1). Because each cross cap has a single circle as a boundary, we must remove only one face from the sphere for each cross cap that we add. Again, assume that this face is a triangle. Using the same rationale as above, when we add a cross cap, the numbers of edges and vertices decrease by 3 and the number of faces decreases by 1. So after adding a cross cap, V − E + F decreases by 1. For a sphere with one cross cap we have
V − E + F = χ(sphere) + χ(cross cap) −1 = 1.
We conclude that the Euler number of the projective plane (a sphere with one cross cap) is 1. When we add c cross caps we obtain
χ(sphere with c cross caps) = 2 − c.
We now know how to compute the Euler number of any surface that can be obtained from a sphere by adding handles and cross caps. An important question remains—are there any surfaces that cannot be obtained in this way? In other words, can we describe all of the possible surfaces in terms of handles and cross caps? Using mathematical jargon, we ask: is it possible to classify all surfaces?
In mathematics, classification theorems are typically difficult or impossible. It is no wonder that Euler never completed his classification of polyhedra. However, occasionally it is possible to classify mathematical objects. After all, Theaetetus classified all regular polyhedra and Archimedes classified all semiregular polyhedra.
Remarkably, it is possible to classify surfaces (with and without boundary). Every closed surface is homeomorphic to a sphere with handles or a sphere with cross caps. That is, every orientable surface is topologically the same as a multi-holed torus, and every nonorientable surface is the same as a sphere with one or more Möbius bands attached to it. In fact, the theorem is stronger than this. If we are given some arbitrary closed surface and we know the Euler number and whether it is orientable or not, then we can identify the surface precisely.
CLASSIFICATION THEOREM FOR SURFACES
A closed surface is uniquely determined by its Euler number and its orientability. An orientable surface is homeomorphic to a sphere with g handles, for some g ≥ 0. A nonorientable surface is homeomorphic to a sphere with c crosscaps, for some c > 0.
For example, suppose S is an orientable closed surface with Euler number −6. Since S is orientable we know that it is homeomorphic to a surface of genus g (a sphere with g handles), where −6 = χ(S) = 2 − 2g. That is, S is homeomorphic to a 4-holed torus. Likewise, if T is a nonorientable closed surface with Euler number −4, then it is homeomorphic to a sphere with c cross caps, where −4 = χ(T) = 2 − c. In other words, T is homeomorphic to a sphere with 6 cross caps.
A similar classification theorem holds for surfaces with boundary. Any surface with boundary is one of these standard surfaces with one or more disks removed. The Euler number, the orientability, and the number of boundary components determine the surface precisely. The only orientable surface with Euler number 0 and two boundary components is a cylinder, the only nonorientable surface with Euler number 0 and one boundary component is a Möbius band, and so on (see table 17.1).
In a sense, it was Bernhard Riemann (1826–1866) in the 1850s who began the classification process. Riemann was one of the preeminent mathematicians of the nineteenth century. He earned his doctoral degree at Göttingen under Gauss at the very end of Gauss’s career. At that time Göttingen was not a center of mathematics in Germany (Gauss taught only introductory courses), so Riemann did much of his graduate work at the University of Berlin.
TABLE 17.1:
The Euler number, orientability, and number of boundaries for different surfaces.
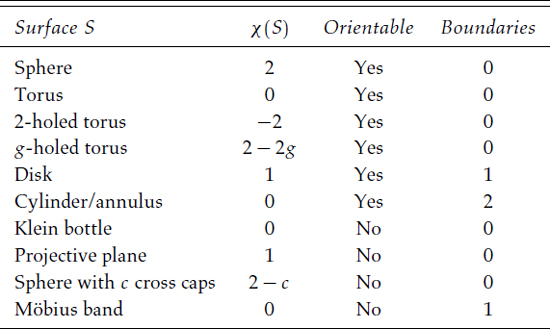
Figure 17.8. Bernhard Riemann.
His brilliance was recognized early. Gauss, who did not give praise lightly, was impressed by Riemann’s first public lecture, given in 1854. Freudenthal describes this lecture as:
One of the highlights in the history of mathematics: young, timid Riemann lecturing to the aged, legendary Gauss, who would not live past the next spring, on consequences of ideas the old man must have recognized as his own and which he had long secretly cultivated. W. Weber recounts how perplexed Gauss was, and how with unusual emotion he praised Riemann’s profundity on their way home.5
Much of Riemann’s work was in complex analysis—the study of complex numbers and complex functions. A complex number has the form a + bi, where a and b are real numbers and 
. It was in a quest for a complete understanding of complex functions that most of his work originated—function theory, geometry, partial differential equations, and topology. Some of his work appeared posthumously, including his treatment of integration, which is now a staple of every introductory calculus course. It is unfortunate that the life of this original thinker was cut short by tuberculosis at the age of forty.
Riemann’s interest in surfaces did not come from the theory of polyhedra, but from complex analysis. Because the complex numbers have two degrees of freedom (a and b), the collection of complex numbers forms a two dimensional plane—it looks like the Euclidean plane except one axis is real and the other one is imaginary.
Riemann was studying multivalued complex functions. For example, consider the function 
. What is the value of f(16)? It is a number w with the property that w4 = 16. It is not difficult to see that there are four such complex numbers, 2, −2, 2i, and −2i. Thus, a single input has more than one output. One way to think of this is that the graph of the function has several layers, or branches. Riemann cleverly interpreted this layered graph as a surface, now called a Riemann surface. A Riemann surface can have quite interesting topology, but is always orientable.
It was in this way that Riemann began his investigations of topology. He introduced the genus of a surface (and the related concept of connectivity, which we will discuss in chapter 22). He grouped together orientable surfaces according to their genus, and he recognized intuitively that two topologically equivalent surfaces must have the same genus.6 Despite this grouping of like surfaces, he did not recognize the converse: that two surfaces with the same genus are topologically the same.
Möbius was the first person to state and prove the classification theorem for orientable surfaces. Möbius had a tool that Riemann did not have. In 1863 he developed the idea of an elementary relationship (essentially what we call a homeomorphism). So he was able to say with some precision what it meant for two surfaces to be the same. Möbius showed that every orientable surface was topologically the same as one of the normal forms shown in figure 17.9—a sphere, a torus, a double torus, and so on.7
In 1866 Camille Jordan proved that any two orientable surfaces with boundary are homeomorphic if and only if they have the same genus and the same number of boundary components.8 The first complete statement and proof of the classification theorem, including nonorientable surfaces, was due to Dyck in 1888.9 However this was still before the modern definitions of surface and homeomorphism. The first truly rigorous proof of the classification theorem is due to Max Dehn (1878–1952) and Poul Heegaard (1871–1948) in 1907.10
Figure 17.9. Möbius’s normal forms for orientable surfaces.
We will not prove the classification theorem, but there are a number of readable demonstrations. Some entail building up the surface to obtain a sphere with handles and cross caps. For instance, John Conway’s ZIP proof (“zero irrelevancy proof”) starts with a pile of triangles—the unassembled puzzle pieces of a triangulated surface. As each new triangle is zipped onto the ever-expanding surface, it remains a sphere with handles, cross caps, and boundary.11 Other proofs work in reverse—they begin with a surface and repeatedly cut out cylinders and Möbius bands (i.e., handles and cross caps), filling in the holes with disks at each stage until arriving at a sphere.
At first glance it may seem that it would be easy to determine the genus of an orientable surface—after all, it is just a sphere with handles. However, they do not always look like one of Möbius’s normal forms. For example, the first surface in figure 17.10 is an example of a sphere with 4 handles—it is homeomorphic to a 4-holed torus.
The classification theorem says that every surface is homeomorphic to a sphere with handles or a sphere with cross caps. It does not say anything about mixing the two. For instance, the second picture in figure 17.10 is a sphere with one handle and one cross cap. How does this fit into the classification? According to our calculations above, the sphere has Euler number 2, adding a handle decreases it by 2, and adding a cross cap decreases it by 1. So the Euler number of this surface is −1. Because of the presence of the cross cap, we know that the surface is nonorientable. According to the classification theorem, it is homeomorphic to a sphere with three cross caps, a surface known as Dyck’s surface.12
Figure 17.10. Unusual surfaces.
A quick inspection of the third surface in figure 17.10 shows that it is two-sided (orientable) and has only one boundary component. Interestingly, the boundary itself forms what is called a trefoil knot. As we will see in the next chapter, any knot can be obtained as the boundary of an orientable surface with one boundary component. By forming a partition of this surface and counting vertices, edges, and faces, we find that the Euler number is −1. By the classification theorem for surfaces with boundary, this surface is homeomorphic to a torus with a disk removed.
As a final example we return to the great icosahedron and the great dodecahedron—the Kepler-Poinsot polyhedra with triangular and pentagonal faces (see chapter 15). Although they do not look like it, they are orientable surfaces (with self-intersections in 3-dimensional space). The Euler number of the great icosahedron is 2, so it is homeomorphic to a sphere, and the Euler number of the great dodecahedron is −6, so it is homeomorphic to a 4-holed torus.