CHAPTER 8
PLATONIC SOLIDS, GOLF BALLS, FULLERENES, AND GEODESIC DOMES
“That’s great, but what’s it good for?” the skeptical student asks, sarcasm dripping from his voice. Beauty is a wonderful trait, but some say usefulness is a more important measure of the worth of a theorem. What is Euler’s formula good for?
That is a fair question to ask of any mathematical theorem. Euler’s formula is more than just an elegant theorem. In the chapters that follow we will present many applications of Euler’s formula. Most will require constructing the appropriate framework to understand the application. To whet the reader’s appetite, we pause now and give two quick applications. First, we prove the uniqueness of the Platonic solids using Euler’s formula, then we use Euler’s formula to derive a structure theorem for golf balls, large molecules, and geodesic domes.
In chapter 5 we gave Euclid’s proof that there are exactly five Platonic solids. Although his proof seems short, it relied on many of the geometric theorems proved in the previous twelve books of his Elements. In this chapter we give a different proof of the uniqueness of the five Platonic solids, one that uses only Euler’s formula and a little arithmetic.
Suppose we have a regular solid. We will show that it must be one of the five known Platonic solids: the tetrahedron, the cube, the octahedron, the icosahedron, or the dodecahedron. Assume that the polyhedron has V vertices, E edges, and F faces. From Euler’s formula we know that
V − E + F = 2.
Because the polyhedron is regular, each face is a regular polygon with the same number of edges. Obviously, this number, call it n, must be at least three. By definition the same number of edges meet at each vertex. This number, m, must also be at least three (of course, m is also the number of faces that meet at each vertex).
Each face contributes n edges, but because each edge is shared by two faces, the quantity Fn counts every edge twice. In other words,
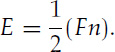
Similarly, each face contributes n vertices, but m faces meet at each vertex, so the quantity Fn counts each vertex m times. So,

Now we substitute these quantities into the Euler’s formula, and solve for F.

We know that 4m and F are both positive. So for this last equation to be true, it must be the case that
2n − mn + 2m > 0.
It is easy to check that only five pairs of integers (n,m) satisfy this inequality, along with the requirements n ≥ 3 and m ≥ 3. Those are: (3, 3), (3, 4), (3, 5), (4, 3), and (5, 3). Using the formulas for V, E, and F from above, we find that these correspond to the five Platonic solids (table 8.1).
TABLE 8.1:
Only five pairs of integers (n, m) satisfy the requirements for a regular polyhedron.


Figure 8.1. Cube-like shapes.
We should reflect upon how surprising this proof is. Euclid’s proof was local and geometrical. He used the angle measures of the regular faces to determine the possible configurations at the vertices. He used this local information to draw a conclusion about the global nature of the polyhedron.
This proof, on the other hand, is global and is virtually devoid of geometry. The theorem is about regular solids, but nowhere in the proof did we use the fact that the faces were regular polygons! We never even assumed that the faces were congruent. Euler’s formula is combinatorial— it counts the numbers of vertices, edges, and faces. It is not possible to incorporate side lengths and angle measures into Euler’s formula, yet we were able to use it to determine the Platonic solids.
Because we did not use all of the hypotheses of the theorem, we must have proved something different. What we did assume was that every face had the same number of sides, and that the same number of faces met at each vertex. From this point of view, all the shapes in figure 8.1 look the same—they all look like a cube.
Figure 8.2. A golf ball composed of 220 hexagons and 12 pentagons.
Essentially we proved that there are only five configurations of polyhedra with the property that every face has the same number of sides and the same number of faces meet at each vertex. Any such polyhedron must “resemble” a tetrahedron, an octahedron, an icosahedron, a cube, or a dodecahedron, just as the polyhedra in figure 8.1 all resemble a cube. In particular, the numbers of vertices, edges, and faces must be the same as one of the five Platonic solids.
In order to create golf balls that were more efficient flyers, one company invented polyhedral golf balls. Instead of a ball covered by round dimples, the exterior of their ball is constructed from 232 indented polygonal faces (see figure 8.2). A quick glance at the surface of the ball reveals a sea of hexagonal faces. Rest assured, however; this ball is not a sixth Platonic solid. Upon closer inspection, we find that 12 of the faces are pentagons.
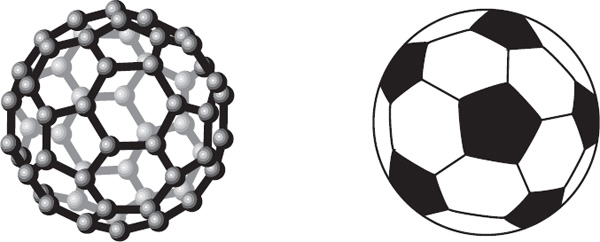
In the introduction we learned about the family of ball-shaped, all-carbon molecules called fullerenes. In figure 8.3 we see the buckminsterfullerene, C60, which has the same shape as a soccer ball. The carbon atoms form 12 pentagonal rings and 20 hexagonal ones. Scientists are able to create fullerenes with other numbers of carbon atoms. For example, C540 is a massive fullerene with 540 carbon atoms. The polyhedral structure of this molecule consists of 12 pentagons and 260 hexagons. In fact, every fullerene has pentagonal and hexagonal rings, and the number of pentagons is always 12.
Figure 8.3. Fullerenes and soccer balls have exactly twelve pentagons.
The following theorem shows that this is not a coincidence. We use the term degree to indicate the number of edges meeting at a vertex.
TWELVE PENTAGON THEOREM
If every face of a polyhedron is a pentagon or a hexagon and if the degree of every vertex is three, then the polyhedron has exactly twelve pentagonal faces.
This theorem is a straightforward application of Euler’s formula. Suppose we have such a polyhedron, with P pentagonal faces and H hexagonal ones. Since each pentagon has five sides and each hexagon has six sides, and since each edge borders two faces, the number of edges is E = (5P + 6H)/2. Likewise, since each vertex has degree 3, the number of vertices is V = (5P + 6H)/3. Inserting these quantities into Euler’s formula yields
2 = V − E + F = (5P + 6H)/3 − (5P + 6H)/2 + (P + H).
By multiplying both sides by 6 we obtain the desired conclusion:
12 = 10P + 12H − 15P − 18H + 6P + 6H = P.
The twelve pentagon theorem has a dual formulation, which we obtain by interchanging the roles of the faces and vertices. We leave the proof of the theorem to the reader.
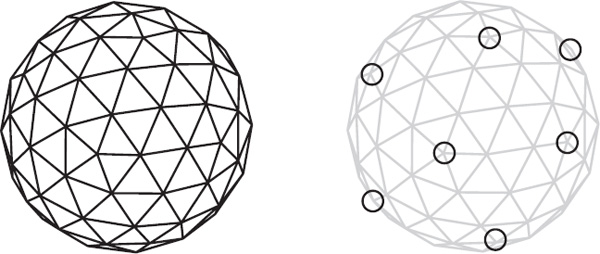
If every face of a polyhedron is a triangle and the degree of every vertex is five or six, then the polyhedron has exactly twelve vertices of degree five.
Figure 8.4. A geodesic dome with twelve vertices of degree five.
In figure 8.4 we see an example of such a polyhedron, with 7 of the 12 degree-five vertices highlighted. Many geodesic domes, such as the Biosphere in Montreal, are based on this design. Of course, architectural geodesic domes are not usually complete spheres. The Epcot Center in Disney World is based on this design, but each triangular face is subdivided into three more triangles.
With these simple examples we get our first glimpse of the power of Euler’s formula. We see how a simple counting formula can force certain properties of polyhedra. In the chapters that follow we will see the great power behind Euler’s seemingly elementary relation.