CHAPTER 4
THE PYTHAGOREAN BROTHERHOOD AND PLATO’S ATOMIC THEORY
The early history of Greek mathematics is full of apocrypha, speculations, contradictory evidence, secondhand accounts, and just enough verifiable truths to create a fascinating puzzle. There are very few surviving records of Greek mathematics, and this scarcity of information makes it challenging to reconstruct the historical truth. Primary sources survived for several centuries after their creation, but nearly all were destroyed or lost during the Dark or Middle Ages. Much of what we know is not drawn from primary sources but from secondary sources written hundreds of years later.
We know little with certainty about Pythagoras (c. 560–480 BCE) and his band of followers, the Pythagoreans. As the philosopher W. Burkert wrote, “One is tempted to say that there is not a single detail in the life of Pythagoras that stands uncontradicted.”2 We believe the Pythagoreans were the first to study the regular solids. Pythagoras is said to have known of the cube and the tetrahedron, and there is a longstanding scholarly disagreement over whether he also knew of the icosahedron and the octahedron. One of his followers is credited with the discovery of the dodecahedron, and as we will see, the discovery may have resulted in his death.
Pythagoras was born on the Greek island of Samos in the Aegean Sea. According to some accounts, he traveled through Egypt and Babylon in his early years and learned their mathematics and religion. Later he settled in the Greek city of Croton in what is now southern Italy.
Figure 4.1. Artist’s rendering of Pythagoras.
Today Pythagoras is associated with the famous geometric theorem that bears his name,* but in his day he was known as a mystic and prophet. In Croton he became the spiritual leader of a secret society based on a philosophical religion. This was a time of religious significance in many cultures (he was a contemporary of Confucius, Buddha, and Lao Tzu). Pythagoras’s successful brotherhood survived in Italy for nearly two hundred years after his death, and his doctrines continued to be taught until the sixth century CE. As time passed, Pythagoras’s legend as a divine figure was enhanced by tales of miracles he performed.
In many ways the Pythagorean brotherhood was not unlike other cults of the day. The members were chosen very carefully—they participated in an initiation, endured ritual purifications, and took a vow of secrecy. They lived by a set of strict, sometimes bizarre, rules. According to legend, they were vegetarians, but were prohibited from eating beans; they could not stir a fire with a knife; they could not wear rings; and they had to touch the earth when it thundered.
The Pythagoreans believed in the transmigration of souls—that the souls of the dead returned as animals, and entered an infinite cycle of reincarnation moving up or down through the ranks of animals and humans. The only way to escape this cycle was through purification of body and mind. As in many cults, the purification of the body was achieved through modest living, abstinence, and restraint.
What distinguished the Pythagoreans was their means of purifying the mind. They did not achieve purity by meditating, but by studying mathematics and science. The ultimate union with the divine was said to follow from an understanding of the order of the universe, and the key to understanding the universe was to understand mathematics. Pythagoras said, “Beatitude is the knowledge of the perfection of the numbers of the soul.”3 This belief is expressed very succinctly by the Pythagoreans’ motto, “All is number.”
The Pythagoreans believed that God ordered the universe with numbers, and that every number could be expressed as a ratio of two whole numbers (every number could be written as a fraction). Using modern terminology, the Pythagoreans believed that all numbers are rational.
Music and astronomy were also important to the Pythagoreans. They discovered that musical intervals could be expressed as ratios and concluded that the most beautiful harmonies came from the most beautiful combinations of numbers. They contended that by using musical ratios one could explain astronomical phenomena such as the distances between the planets, the order of the planets, and the periods of revolution. They believed that the movement of the seven known planets (which included the earth, moon, and sun), like the vibrations of the seven strings of the lyre, created a harmony. Some claimed that this “music of the spheres” was audible to Pythagoras.
The Pythagoreans followed a communal lifestyle; they ate meals, exercised, and studied together. This way of living, along with their tradition of sharing knowledge orally, their enforced secrecy, and their adoration of Pythagoras, makes it difficult to discern which Pythagorean made what contribution to mathematics. In fact, since mathematics was part of their religion, and Pythagoras was their spiritual leader, any mathematical result obtained by his followers was “the word of the master” and was attributed to him.
According to legend, one of the Pythagoreans, Hippasus of Metapontum (c. 500 BCE), did not follow this tradition of deference, and was severely disciplined. One account states that he was drowned at sea, while another contends that he was expelled from the Pythagoreans and a tombstone was erected for him as a symbolic send-off. Again, accounts differ on what Hippasus had done to deserve this harsh treatment, and there are two competing stories (both of which may be true).
Figure 4.2. A pentagram, the symbol for the Pythagorean school, inscribed in a regular pentagon.
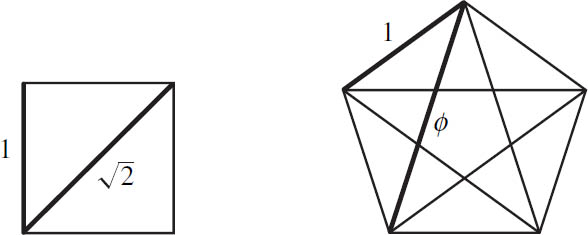
Figure 4.3. Diagonals of irrational length,
and Ø = 
One tale suggests that Hippasus discovered the dodecahedron and showed how to inscribe it in a sphere, but he failed to give credit to Pythagoras. This discovery may have been especially meaningful to the Pythagoreans because of the dodecahedron’s pentagonal faces. They adopted the pentagram, or pentagon-star (see figure 4.2), which was the Greek symbol for health, as the special symbol used to identify others in the brotherhood. The pentagram is created by connecting the vertices of a regular pentagon, and doing so creates a new regular pentagon inside it.
The second tale states that Hippasus proved that not every number is rational, and he failed to keep this discovery a secret. Historians disagree over which irrational number Hippasus discovered. It could be , which is the length of the diagonal of a square with sides of length 1, or it could be (
+ 1)/2, which is frequently called the golden ratio, or simply ø. That Hippasus discovered the irrationality of the golden ratio is an attractive theory because ø happens to be the length of the side of a pentagram that is inscribed in a pentagon with sides of length 1 (see figure 4.3). That all numbers are rational was one of the supporting pillars of the Pythagoreans’ system of beliefs. The existence of an irrational number was a devastating and damaging realization. It is in this light that we can imagine their outrage at Hippasus. Ironically, the proof of the existence of an irrational number is one of the most significant and lasting contributions of the Pythagoreans to mathematics.
Regardless of whether it was Hippasus or one of his fellow Pythagoreans who discovered the dodecahedron, the Pythagoreans seemed to know of at least three of the regular solids: the tetrahedron, the cube, and the dodecahedron. It is not clear if they knew of the octahedron and the icosahedron, or if the discovery of these polyhedra should be attributed to Theaetetus of Athens (c. 417–369 BCE). Even early evidence is contradictory. Proclus (410–485), the fifth-century scholar, claims that the Pythagoreans knew of the octahedron and the icosahedron, whereas an undated scholium to Euclid’s Elements states that “three of the aforesaid five figures [are] due to the Pythagoreans, namely the cube, the pyramid and the dodecahedron, while the octahedron and the icosahedron are due to Theaetetus.”4 Today, many scholars subscribe to William Waterhouse’s theory of the late discovery of the octahedron, which would seem to rule out the Pythagoreans as discoverers.
Theaetetus is not as famous as some other Greek mathematicians, but he is unquestionably a hero of this story. He is almost certainly responsible for proving that there are five and only five regular polyhedra. Much of what we know about Theaetetus we know from the writings of his friend, the influential philosopher and teacher, Plato (427–347 BCE). Plato wrote two dialogues featuring Theaetetus: The Sophist and the eponymous Theaetetus.
Theaetetus was born during the Peloponnesian War. He died a war hero following the 369 BCE battle between Athens and Corinth. He studied mathematics under Theodorus (465–398 BCE), and by all accounts was a very gifted mathematician. Plato held Theaetetus in highest regard, second only to his teacher, Socrates (470–399 BCE). In Plato’s Theaetetus, Theodorus says of the young Theaetetus, “This boy advances toward learning and investigation smoothly and surely and successfully, with perfect gentleness, like a stream of oil that flows without a sound, so that one marvels how he accomplishes all this at his age.”5
At this time, the discovery of irrational numbers was a relatively recent event and not much was known about their properties. Theaetetus made important contributions to the classification and organization of irrationals. Later this classification would constitute most of Book X of Euclid’s Elements.
Figure 4.4. Artist’s rendering of Plato.
Despite the disagreement over who was the first to discover each of the five regular solids, there is little doubt that Theaetetus was the first to bring the study of the solids into a complete and rigorous form. Thanks to Theaetetus, the three phases of development that we discussed in chapter 3 were fulfilled. First, all five solids were known and Theatetus was able to construct them geometrically. Second, he perceived the common trait binding these five polyhedra—their regularity. Finally, he proved that these five solids are the only regular polyhedra. Theaetetus’s proofs and constructions appeared later in Book XIII of Euclid’s Elements. In fact, many historians contend that all of the mathematics in Books X and XIII of the Elements is due to Theaetetus.
Today Plato is best known as a philosopher and a writer, but one of his most important contributions was the creation of his school, the Academy. The Academy opened in the outskirts of Athens in approximately 288 BCE, a decade after the execution of Socrates. Plato founded the Academy to prepare young men for public life through the study of science and, especially, mathematics. It was his belief that by studying mathematics we learn to separate our intellect from our senses and our opinions. The Academy remained in existence for over nine hundred years. Its founding has been called “in some ways the most memorable event in the history of Western European science.”6
Plato is not known for adding to the body of mathematics, but he was an important figure in the advancement of the subject. He was a lover of mathematics, and he held mathematicians in high regard. Mathematics formed the backbone of the curriculum at the Academy. This is clearly illustrated by the inscription found above its entrance: “Let no one ignorant of geometry enter here.” Because many mathematicians were trained and nurtured in the Academy, it is said that Plato was not a maker of mathematics, but “a maker of mathematicians.”7
As head of the Academy, Plato left much of the specific instruction to others. Theaetetus was one of these instructors, and it is believed that he taught at the Academy for fifteen years.8
It was from Theaetetus that Plato learned of the five regular solids. Plato recognized their mathematical importance and their beauty. Like many future thinkers, he believed that there must be cosmic significance for this magnificent collection of five objects. Plato was familiar with the view of the universe put forth by Empedocles (c. 492–432 BCE) stating that all matter is created from four primal elements: earth, air, fire, and water. These four building blocks feature prominently in Plato’s Timaeus, a fictional account of a discussion between Socrates, Hermocrates, Critias, and Timaeus. Through a long monologue by the Pythagorean Timaeus of Locri, Plato laid out an elaborate atomic model, wherein each of the four elements, which Plato called bodies or corpuscles, is associated with one of the regular solids:
To earth let us give the cube, because of the four kinds of bodies earth is the most immobile and the most pliable—which is what the solid whose faces are the most secure must of necessity turn out to be, more so than the others . . . And of the solid figures that are left, we shall next assign the least mobile of them to water, to fire the most mobile, and to air the one in between. This means that the tiniest body belongs to fire, the largest to water, and the intermediate one to air—and also that the body with the sharpest edges belongs to fire, the next sharpest to air, and the third sharpest to water.
Using this rationale Timaeus concluded that fire is a tetrahedron, air an octahedron, and water an icosahedron. The fifth regular solid, the dodecahedron, could not be one of the elements. Timaeus contended that “this one the god used for the whole universe, embroidering figures on it.”9
Timaeus went on to describe the interactions of the elements. The interactions are based on cutting and crushing; the sharper the element, the more it tends to cut, the less sharp, the more it tends to crush. This enables what we would describe as chemical reactions among fire, air, and water (but not earth, since it has square faces). The elements break apart and the triangular faces reform to create other elements. For example, one element of water (consisting of 20 equilateral triangles) can be broken apart and reformed to make three fire elements (3 · 4 = 12 triangles) and one element of air (8 triangles). Timaeus noted that the different varieties of matter can be explained by the different sizes of the elements. He also addressed the phenomena of phase change: melting and freezing. For example, he would argue that metal is liquefiable water (as opposed to liquid water) that is composed of very large uniform icosahedrons which make it appear solid. When the sharp fiery tetrahedrons are applied to it, the icosahedrons separate from one another, the metal melts, and it is able to flow as a liquid.
The belief that earth, air, fire, and water are the four primal elements was adopted and expanded by Aristotle (384–322 BCE), a student of Plato. It was Aristotle who elevated the ether to be the fifth element, or quintessence, and argued that it was the material from which the heavenly bodies were made.
The Greek atomic model was so influential that it was universally accepted until the birth of modern chemistry two thousand years later. It was not until the Irish scientist Robert Boyle (1627–1691) published his book The Sceptical Chymist in 1661 that this chemical model began to crumble.
Although the Greek theory of chemistry is now a distant memory, the legacy remains. We still speak of being “exposed to the elements” when we step out into the wind (air) and rain (water). The elements appear implicitly and explicitly in many works of literature, pieces of artwork, mystical religions, fantasy games, and elsewhere. Some go so far as to argue that successful foursomes can be accurately paired with the elements (fire: John Lennon; water: Paul McCartney; air: George Harrison; earth: Ringo Starr).
Ever since Plato’s treatment of the regular solids in Timaeus, the five regular polyhedra have been known as the Platonic solids.
* The Pythagorean theorem states that if the legs and the hypotenuse of a right triangle have lengths a, b, and c, respectively, then a2 + b2 = c2. In fact, this relationship was known to the Babylonians over a thousand years earlier.