CHAPTER 12
CAUCHY’S FLATTENED POLYHEDRA
In the hundred years after Euler’s proof of his polyhedron formula, there were many new proofs and a variety of generalizations to exotic polyhedral shapes. The first significant generalization came from Augustin-Louis Cauchy, who also gave an ingenious new proof.
Cauchy was born in Paris in 1789. He was the eldest son of a senior government administrator. Although his family was displaced during the Reign of Terror, his father saw that he received a good education. As a youth he became acquainted with the mathematicians Pierre-Simon Laplace (1749–1827) and Joseph-Louis Lagrange, and the chemist Claude Louis Berthollet (1748–1822), so he was exposed early in his life to influential scholars.
Cauchy had a brief career as a military engineer working on the Ourcq Canal, the Saint-Cloud Bridge, and the Cherbourg naval base. His first mathematical publications were composed in 1811, two years before before he returned to Paris to begin a mathematical career. In 1815 he began his employment at the École Polytechnique.
Cauchy was extremely prolific. His voluminous output was second only to Euler’s; his collected works, which include at least seven books and eight hundred papers, fill twenty-seven sizable volumes. Although it is likely apocrypha, it was said that a newly-instituted rule at the French Academy limiting the number of publications per contributor per year was in response to the deluge of publications flowing from Cauchy’s pen.
Cauchy made deep and substantial contributions to many areas of mathematics, including complex analysis, real analysis, algebra, differential equations, probability, determinants, and mathematical physics. He was one of the early champions of the need for rigor in mathematics. Many of the fundamental ideas of calculus introduced by Newton, Leibniz, Euler, and others were finally placed on a firm theoretical foundation by Cauchy. We can thank him for what are essentially the modern definitions of continuity, limit, derivative, and definite integral. Through his frequent lectures at the École Polytechnique and his numerous publications, his was an ever-present voice in the mathematical community for the first half of the nineteenth century.

Figure 12.1. Augustin-Louis Cauchy.
It is a testament to Cauchy’s influence that there are so many theorems, properties, and concepts named after him—perhaps more than for any other mathematician, even Euler. Yet it seems that Cauchy became one of the great mathematicians in spite of himself. He often published great works without seeming to recognize their depth and importance. The mathematician Hans Freudenthal (1905–1990) wrote, “In nearly all cases he left the final form of his discoveries to the next generation. In all that Cauchy achieved there is an unusual lack of profundity . . . He was the most superficial of the great mathematicians, the one who had a sure feeling for what was simple and fundamental without realizing it.”2
Although Cauchy was greatly admired as a mathematician, he was not usually admired as a person. He was known to be stubborn, and he had a flair for melodrama. These traits are typified by a self-imposed exile from France to Turin and Prague that lasted almost a decade. He was a political conservative who followed the ousted Bourbon king Charles X after the July Revolution of 1830. Before he left France and after he returned, he refused to swear the required oath of allegiance to the new regime or even to agree not to speak out. He was a staunch Catholic whose charitable actions were overshadowed by behavior that betrayed him as a “bigoted, selfish, narrow-minded fanatic.”3 One biographer wrote that Cauchy was “an arrogant royalist in politics and a self-righteous, preaching, pious believer in religion . . . most of his fellow scientists disliked him and considered him a smug hypocrite.”4

Figure 12.2. Cauchy projected the polyhedron into the bottom face.
Cauchy wrote his first mathematical papers while he was still an engineer. These papers contain his results on polyhedra, including his rigidity theorem (which we discussed in chapter 5) and his work on Euler’s formula. These important results were among the very few contributions Cauchy made to geometry.
The first notable feature that distinguishes Cauchy’s proof of Euler’s formula from those of his predecessors is that the polyhedra in his proof are hollow, not solid. More specifically, he considers the “convex surface of a polyhedron.”5 Because of this language and because elsewhere in the paper he carves a polyhedron into smaller polyhedra, it appears that he still views a polyhedron as solid, and only for the purpose of the proof does he assume that it is hollow.
The first step in Cauchy’s proof is to transform this hollow polyhedron into a graph in the plane. He removes a face from the polyhedron, then “by transporting onto this face all the other vertices without changing their number, one will obtain a planar figure made up of several polygons contained in a given contour.” Cauchy clarifies this instruction by saying that “the remaining faces . . . could be regarded as forming a suite of polygons contained in the outline of the removed face.” We see this process illustrated in figure 12.2, where the house-shaped polyhedron is transported onto the ground floor.
Figure 12.3. The flattened polyhedron viewed as a shadow of the edges.
Joseph Diaz Gergonne (1771–1859), a contemporary of Cauchy’s whom we will meet in chapter 15, described this process as follows:
Take a polyhedron, one of its faces being transparent; and imagine that the eye approaches this face from the outside so closely that it can perceive the inside of all the other faces; this is always possible when the polyhedron is convex. The things being so arranged, let us imagine that on the plane of the transparent face a perspective is made of the set of all the others.6
In his wonderful book Proofs and Refutations, Imre Lakatos (1922–1974) put a modern spin on Gergonne’s idea by suggesting that a camera be placed near the removed face, and the inside of the polyhedron be photographed. The graph would then appear on the photographic print. Yet another common way of visualizing this flattened polyhedron is as the shadow of the edges when a light bulb is situated near the removed face (figure 12.3).
Cauchy realized that it sufficed to understand the relative numbers of vertices, edges, and faces in the graph. Cauchy proved that every such graph satisfies V − E + F = 1. Once he established this fact, it was easy to complete the proof of the polyhedron formula. The graph obtained from transporting the polyhedron onto the plane has the same number of edges and vertices as the polyhedron, but it has one fewer face. Because V − E + F = 1 for the graph, V − E + F = 2 for the polyhedron. Cauchy’s adaptation of Euler’s formula to graphs in the plane is one of the most useful generalizations.
The idea of Cauchy’s proof is to add and remove edges in such a way that at each step the quantity V − E + F does not change. Then in the end, we obtain a single triangle, which satisfies V − E + F = 3 − 3 + 1 = 1, implying that V − E + F = 1 for the original graph. The first step in Cauchy’s proof is to divide the graph into triangular regions by adding diagonals to all nontriangular faces (see figure 12.4). This procedure is called triangulating a graph. Each time a diagonal is added, the number of edges increases by one, the number of faces increases by one, and the number of vertices remains the same. Thus V − E + F is the same for the original graph as for the modified graph. Once the graph has been triangulated, we decompose it by removing triangles from the outside, one at a time, until a single triangle remains (one possible order is given by the labels in figure 12.4).

Figure 12.4. The order of triangle removal from the triangulated graph.
Notice that a triangle on the outside of the graph has either one or two exterior edges. In the first case the triangle can be removed by taking away the single edge and no vertices (such as the removal of triangle number 1). In the second case the triangle can be removed by taking away two edges and a vertex (such as the removal of triangle number 2). In either case, the quantity V − E + F remains unchanged. Thus, it must be the case that V − E + F = 1 for the original graph.
Cauchy’s proof was later criticized. Just as Euler ran into trouble by failing to give explicit instructions on what order to remove the pyramids, Cauchy did not give reliable instructions on how to cut away the triangles. If we are not careful, it is possible to follow Cauchy’s algorithm and obtain a disconnected graph for which the relation fails to hold. For instance, in figure 12.5 we removed triangles in the wrong order and obtained a disconnected graph that fails to satisfy Euler’s formula (V = 10, E = 14, and F = 6). Nonetheless, it is always possible to use Cauchy’s technique to decompose a graph without this situation occurring.
As we have already mentioned, Cauchy had a track record for proving theorems without realizing their importance or without following them to their logical conclusions. His proof of Euler’s polyhedron formula is a perfect example of this. In his paper he makes the explicit assertion that his proof applies to convex polyhedra. Indeed it does, but it actually applies to a much more general class of polyhedra. The key step in Cauchy’s proof is removing a face and transporting the rest of the polyhedron onto the plane in such a way that none of the faces overlap. This can be accomplished for any convex polyhedron, but it can also be accomplished for many other polyhedra.

Figure 12.5. Cauchy’s method can yield a degenerate polygon.
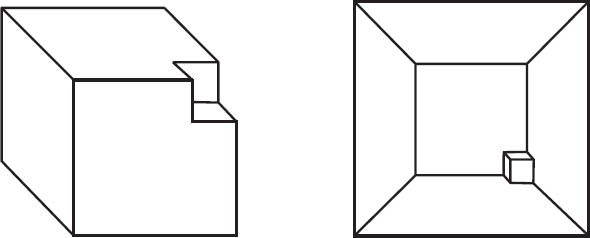
Figure 12.6. A cube with an indented corner and its graph.
For instance, Cauchy’s proof applies without modification to the non-convex polyhedron shown in figure 12.6. To see this, simply place Lakatos’s camera near the bottom face of the cube.
Lakatos and the mathematician Ernst Steinitz (1871–1928) claim that Cauchy knew his proof applied to some or perhaps all nonconvex polyhedra, but this is not clear from what Cauchy wrote. The discrepancy arises from Cauchy’s casual use of the word “convex.” It did not appear in the statement of the theorem, but in the proof he said he was considering “the convex surface of a polyhedron.” He never addressed the discrepancy, so it is impossible to guess what he did and did not know.
Regardless of whether Cauchy recognized that the result could be extended to some nonconvex polyhedra, it was quickly seen by others. In 1813, the same year that Cauchy’s paper was published, Gergonne gave his own proof of Euler’s formula. Afterward he wrote, “One might prefer still, with reason, the beautiful proof of Mr. Cauchy, who has the precious advantage of not assuming that the polyhedron is convex.”7
With a little imagination we can apply Cauchy’s proof to a still broader class of polyhedra. Modern versions of Cauchy’s proof describe a polyhedron as made out of rubber. If a face can be removed and the rest of the polyhedron can be stretched out onto the plane without any overlapping or folding, then Cauchy’s proof applies. In chapter 15 we will see pathological examples of polyhedra that do not have this property—when a face is removed, the rest of the polyhedron cannot be transported to the plane. The key property, it turns out, is that the polyhedron is “sphere-shaped.” We will discuss this seemingly vague property in more detail in chapter 16. Cauchy was agonizingly close to recognizing this essential property. Had he noticed this, he would have made a significant contribution to the yetunformed field of topology, or analysis situs as it was known in the early days. As Jacques Hadamard (1865–1963) wrote in 1907:
I consider to be one of the most remarkable events in the history of science, the error which Cauchy made while believing to prove the theorem of Euler without introducing any assumption on the nature of the studied polyhedron. It is indeed a principle of paramount importance which eluded him and which he left for Riemann to discover: the fundamental role of the analysis situs in mathematics.8
Just as Cauchy missed the full strength of his proof for polyhedra, he also did not recognize the full strength of this proof for graphs. For example, it was Arthur Cayley (1821–1895) who, in 1861, observed that Cauchy’s proof applied equally well to graphs that had curved edges (this fact was noticed independently by Listing in 1861 and Camille Jordan [1838–1922] in 1866).9
In the statement of his theorem Cauchy assumed that the graph is a collection of polygons contained in a polygonal outline. As we will see in the next chapter, we can give a much more general statement about graphs, but in order to do so we must introduce some modern terminology.

