CHAPTER 10
LEGENDRE GETS IT RIGHT
The second published proof of Euler’s polyhedron formula, and the first to meet today’s rigorous standards, was given by Adrien-Marie Legendre. Legendre was a French mathematician who belonged to both the Académie des Sciences in Paris and the Royal Society of London. He published in several areas, but his most important contributions were to number theory and the theory of elliptic functions. His legacy also includes an extremely popular textbook on elementary geometry that he wrote in 1794, Élements de géométrie (Elements of Geometry). In many ways Legendre’s Élements replaced Euclid’s Elements, becoming the primary geometry text for the next hundred years, and it became the prototype for future generations of geometry textbooks. It was translated into English several times; one American translation had thirty-three editions.
Legendre included Euler’s polyhedron formula in Elements of Geometry, and the book’s popularity gave it wide exposure. Legendre did not repair Euler’s proof; instead, he presented a new demonstration—one that differed substantially from Euler’s. Legendre’s ingenious argument used concepts from spherical geometry and metric properties such as angle measures and area. The success of such a proof is especially unexpected because these concepts do not appear in the statement of the theorem.
The key to Legendre’s proof is an elegant formula from spherical geometry that gives the area of a triangle on the surface of a sphere in terms of its interior angles. On a sphere, triangles and other polygonal figures are not made from straight lines but from arcs of great circles. A great circle is any circle on a sphere that has the same radius as the sphere, or, equivalently, it is any circle on the sphere of maximum possible radius. Examples of great circles on the Earth are the equator and lines of longitude. Lines of latitude other than the equator—the Tropics of Cancer and Capricorn, the Arctic Circle—are not great circles. Great circles are not straight, but they are as close to straight as is possible on a sphere. They have the noteworthy property that they are length-minimizing. That is, the shortest path between two points on a sphere follows a great circle. Ignoring physical realities such as wind currents and the rotation of the earth, an airplane flying from Pennsylvania to India seeking the shortest route would fly along a great circle that passes over Iceland.

Figure 10.1. Adrien-Marie Legendre.

Figure 10.2. Lay a ribbon on a sphere to find a great circle.
A practical way to find great circles on a small sphere is to use a ribbon (figure 10.2). Take a wide ribbon such as those on birthday presents and lay it on the sphere. Wrap the ribbon around in such a way that it lies flat and does not twist laterally. When we do this the ribbon traces out a great circle.
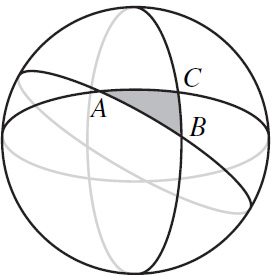
Figure 10.3. A triangle formed by three great circles.
We define a triangle on a sphere to be a region bounded by three great circles (as shown in figure 10.3). In mathematical language a great circle is known as a geodesic, so a more precise name for a spherical triangle is a geodesic triangle. We insist, as Legendre did, that each side of a geodesic triangle is less than half the circumference of the sphere.
Geodesic triangles were first introduced by the Greek mathematician Menelaus of Alexandria (c. 98) in his book Sphaerica. In this book Menelaus presented a theory for spherical geometry that is analogous to Euclid’s theory for planar geometry found in Elements. He showed that many of the theorems for planar triangles are also true for geodesic triangles. For instance, the sum of the lengths of two sides of a spherical triangle is always greater than the length of the third side. He proved an interesting result that is true on a sphere, but not in a plane: two similar geodesic triangles (they have angles of equal measure) must be congruent. On the other hand, one of the most well-known theorems from planar geometry—that the sum of the interior angles of a triangle is 180°, or π radians—does not hold on a sphere.* On a sphere, the sum of the interior angles is always greater than π. For example, the large geodesic triangle shown in figure 10.4 has three right angles; so they sum to 3π/2. The smaller geodesic triangle experiences less of the curvature of the sphere, so the angle sum is smaller—but it still exceeds π.
For nearly fifteen hundred years no one refined Menelaus’s statement about the sum of the interior angles. It was not until the seventeenth century that two men, Thomas Harriot (c. 1560–1621) and Albert Girard (1595–1632), quantified the excess in the angle sum.

Figure 10.4. Geodesic triangles on a sphere.
In figure 10.4 we see that there is a direct relationship between the area of a triangle and the sum of its interior angles. As a triangle grows in size, it becomes more distorted because of the curvature, and the sum of the interior angles grows.
The theorem of Harriot and Girard gives a formula relating three quantities: the sum of the interior angles of a geodesic triangle, the area of the triangle, and the radius of the sphere on which it lies. For simplicity, we shall give the formula for triangles on the unit sphere—the sphere of radius one. (The formula for a sphere of a different radius is obtained by scaling the quantities appropriately.)
HARRIOT-GIRARD THEOREM
The area of a geodesic triangle on the unit sphere with interior angles a, b, and c is a + b + c − π. In other words, area = (angle sum) − π.
Because the sum of the interior angles of every planar triangle is π, we can restate the formula in yet another way:
area = (angle sum) − (angle sum for a planar triangle).
That is, the area of a spherical triangle is precisely the amount that the angle sum exceeds the angle sum of a planar triangle. As we will see, this remarkable formula generalizes to spherical polygons with more than three sides. By the way, this is our first concrete example showing why it is advantageous to measure angles in radians; it is invalid when angles are measured in degrees.
As a warm up exercise, let us verify that this theorem holds for the large geodesic triangle shown in figure 10.4 (assuming that the sphere is the unit sphere). We can cover the sphere with eight of these triangles—four in the northern hemisphere and four more in the southern hemisphere. So the area of this triangle is one-eighth the area of the sphere. Because the surface area of a sphere of radius r is 4πr2, the unit sphere (r = 1) has surface area 4π. Hence, the area of the triangle is one-eighth of 4π, or π/2.
Now we can check that the Harriot-Girard theorem yields the same value. The sum of the three interior angles of this triangle is 3π/2. So, according to the theorem, the area of this triangle must be (3π/2) − π = π/2, which agrees with our previous calculation.
This relationship was discovered independently by Harriot and Girard. The British scholar Thomas Harriot is somewhat of an enigma. He was a talented and active researcher, but he never published any of his work. When he died, he left ten thousand pages of unpublished manuscripts, diagrams, collections of measurements, and calculations. One biographer wrote that Harriot’s aversion to publishing “may largely be explained by adverse external circumstances, procrastination, and his reluctance to publish a tract when he thought that further work might improve it.”2 Many of his papers appeared posthumously. He is best known for his work in algebra, but he also studied optics, astronomy, chemistry, and linguistics. Harriot, like Leibniz and Euler, had a reputation for introducing new and elegant mathematical notation. Unfortunately, because of the difficulty of typesetting his nonstandard notation, not all of it appeared in print and was thus not widely adopted. Two symbols that did survive are the signs < for “less than” and > for “greater than.” Very little is known about Harriot’s personal life. In 1585 he was sent by Sir Walter Raleigh on a one-year trip to the New World as a surveyor and mapmaker. So it is likely that he was the first established mathematician to set foot in North America.
The French mathematician Albert Girard resided in Holland, most likely because he was uncomfortable living in his childhood home of Lorraine, France, as a Protestant. Today he is known for his work in algebra and trigonometry. He has the distinction of being the first to use the abbreviations sin, tan, and sec for the trigonometric functions sine, tangent, and secant, and for introducing the notation ![]() for cube root. Girard was also the first mathematician to assign a geometric significance to negative numbers. He wrote, “The negative solution is explained in geometry by moving backward, and the minus sign moves back when the + advances.”3
for cube root. Girard was also the first mathematician to assign a geometric significance to negative numbers. He wrote, “The negative solution is explained in geometry by moving backward, and the minus sign moves back when the + advances.”3
Historically, the area formula for spherical triangles had Girard’s name attached to it, and not Harriot’s. This attribution is understandable because Girard’s proof, which was published in 1629,4 was the first to appear in print. Girard was known for his terse writing style, and his proofs often suffered from lack of detail. This proof was even unsatisfactory to Girard, himself—he described the result as “a probable conclusion.”5 Unbeknownst to him, the same theorem had been proved by Harriot twenty-six years earlier. Of course, as we have noted, Harriot did not publish this result, or any mathematical result. Nonetheless, he did not keep it a secret. His proof was known to contemporaries; the British mathematician Henry Briggs (1561–1630) had told Kepler of Harriot’s result and had included it in a list of the great discoveries of his time. However, there is no indication that Girard was aware of Harriot’s proof.
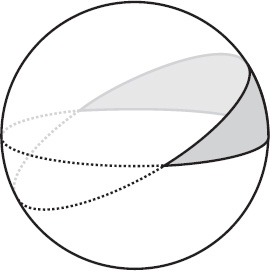
Figure 10.5. A lune on a sphere.
Because Harriot was the first to prove the theorem and Girard was the first to publish it, we now call the result the Harriot-Girard theorem. It is worth noting that Harriot’s proof was much simpler and more elegant than was Girard’s. The argument we give below is due to Legendre, but it is very similar to Harriot’s.
Legendre’s proof cleverly uses an object called a lune (occasionally called a biangle in analogy with a triangle). A lune is a region bounded by two great circles (see figure 10.5). A pair of great circles always meet at two points that lie on the exact opposite sides of the sphere. If the two circles meet with an angle a at one end, then they also meet with angle a at the other end. If the angle a is measured in radians, then the area of the lune (on a unit sphere) is 2a. We easily justify this fact by setting up a simple ratio: the area of the lune is to the total surface area of the sphere as a is to 2π (as can be seen in figure 10.6). So, we have

Solving the equation for the area we find it to be 2a.
Figure 10.6. A lune on a sphere (left) and the view from above (right).

Figure 10.7. Great circles in a hemisphere.
Now, consider a geodesic triangle ABC on a unit sphere with interior angles a, b, and c. The triangle is contained in some hemisphere. Extend the sides of ABC to meet the boundary of this hemisphere. As in figure 10.7, let D, E, F, G, H, and I denote the points where these lines meet the hemisphere’s edge.
By the symmetries of the sphere, the sum of the areas of the regions ADE and AGH is the same as the area of a lune with angle a. In other words, if we were to cut out the triangle AGH and glue edge GH to edge ED, then we would have a lune with angle a. From this observation we conclude that
area(ADE) + area(AGH) = area of lune = 2a.
Similarly, triangles BFG and BDI have the same area as a lune with angle b, and triangles CHI and CEF have the same area as a lune with angle c. So we have
area(BFG) + area(BDI) = 2b
area(CHI) + area(CEF) = 2c.
Summing these three equations gives
[area(ADE) + area(AGH)] + [area(BFG) +
area(BDI)] + [area(CHI) + area(CEF)] = 2a + 2b + 2c.
Looking closely at the left-hand side of this expression, we see that we are adding the area of every region of the hemisphere once, except the triangular region ABC, which we are adding three times. So we have
area(hemisphere) + 2 · area(ABC) = 2a + 2b + 2c.
Because the area of the hemisphere is 2π, we obtain
2π + 2 ∙ area(ABC) = 2a + 2b + 2c.
Rearranging this expression and dividing by 2, we conclude that
area(ABC) = a + b + c − π,
as desired.
For Legendre’s proof of Euler’s formula we need the following generalization of the Harriot-Girard theorem to geodesic polygons with more sides than three.
HARRIOT-GIRARD THEOREM FOR GEODESIC POLYGONS
The area of an n-sided geodesic polygon on the unit sphere with interior angles a1, a2, . . . , an is a1+ ···· + an – nπ + 2π, or equivalently, area = (angle sum) – nπ + 2π.
The sum of the interior angles of any planar polygon with n sides is (n − 2)π. (We will look closely at this theorem and its generalizations in chapter 20.) So, just as with triangles, the area of a geodesic polygon is simply the amount that its angle sum exceeds the angle sum of a planar polygon with the same number of sides. That is,
area = (angle sum) − (angle sum for a planar n-gon).
To see why this generalization holds, divide the polygon into geodesic triangles by adding diagonals. Such a decomposition has n − 2 triangles (see figure 10.8). The sum of the areas of these triangles is the area of the polygon, and the sum of the angles of the triangles equals the sum of the angles of the polygon. Applying the Harriot-Girard theorem to all n − 2 triangles and summing, we find the area of the polygon to be

Figure 10.8. A polygon on a sphere divided into triangles.

Figure 10.9. The area of the spherical polygon is the sum of the quantities on the diagram.
area = a1 +····+ an − (n − 2)π = a1 + ···· + an − nπ + 2π.
There is an easy way to remember this formula. Visualize the polygon as shown in figure 10.9. Place the angle measure at each angle, −π on each edge, and 2π in the middle of the face. The area of the polygon is simply the sum of these quantities. This visual representation will be useful in understanding Legendre’s proof of Euler’s formula.
Finally, we are ready to give Legendre’s argument. Begin with a convex polyhedron with V vertices, E edges, and F faces. Let x be any point in the interior. As shown in figure 10.10, construct a sphere centered at x that surrounds the polyhedron completely. Because the units are unimportant, we may choose them so that the sphere has radius one. Project the polyhedron onto the sphere using rays emanating from x. One way to visualize the projection is to imagine that the polyhedron is a wireframed model and that x is a light bulb. The projection is the shadow of the wire frame on the surface of the encompassing sphere. We will not prove it, but in this case the faces of the polyhedron become geodesic polygons.
Figure 10.10. The projection of a polyhedron onto a sphere.
In his proof, Legendre employed a common mathematical trick. He computed the same quantity—in this case the area of the unit sphere—in two different ways, thereby deriving an equality. First, he used the well- known area formula to find that the surface area of the unit sphere is 4π. Second, he summed the areas of each face on the sphere which, clearly, also gives the overall surface area.
By the Harriot-Girard theorem we know that the area of each n-sided face is the sum of the interior angles minus nπ − 2π. Rather than working with this formula directly, we use the visual representation introduced in figure 10.9. Label all of the angles, edges, and faces on the sphere—placing the angle measure at each angle, −π on both sides of every edge, and 2π in the middle of every face—yielding a sphere such as the one in figure 10.11. To compute the surface area of the sphere we sum all of the labeled quantities.
Although the angles meeting at a vertex of the polyhedron sum to less than 2π, these same angles sum to 2π when projected onto the smooth surface of the sphere. Since there are V vertices, the vertices contribute 2π V to the sum. Each edge contributes −2π; namely, −π from one side and −π from the other side. Since there are E edges, they contribute −2π E to the sum. The middle of each face is labeled with 2π. Since there are F faces, they contribute 2π F to the sum. Putting all of this together we find that the total surface area of the sphere is
4π = 2π V − 2π E + 2π F.
Figure 10.11. The projection with labels.
Dividing by 2π, we obtain Euler’s formula,
2 = V − E + F.
Even a quick comparison of Euler and Legendre is enough to show that their proofs are very different. On the one hand, Euler’s seems to be “the right proof,” or at least it is the right style of proof. The theorem is combinatorial, and Euler gave a combinatorial proof. Euler employed the relationship among vertices, edges, and faces very directly. When a vertex was removed, faces and edges were added or removed to compensate, and doing so did not change the alternating sum.
By contrast, Legendre introduced seemingly unrelated concepts— spheres, angles, and area—to prove the theorem. His approach is valid and very clever, but it does not illustrate why the theorem is true—at least not in a transparent way. Nevertheless, Legendre’s proof gave the first indication that there is more here than simply a combinatorial theorem. The fact that we can prove the theorem using metric geometry suggests an important relationship between Euler’s formula and geometry. We will return to this topic—the relationship between Euler’s formula and geometry—in chapters 20 and 21.
We make one last remark about Legendre’s proof. With Euler’s approach we were careful (more careful than Euler was himself) to apply the formula only to convex polyhedra. Like Euler, Legendre assumed that his polyhedra were convex. However, in the appendix to a paper written in 1809, Louis Poinsot (1777–1859) made the observation that Legendre’s proof applied to a slightly more general class of polyhedra than the convex ones, a class of polyhedra called star-convex.6
The first step in Legendre’s proof was to project the polyhedron onto the sphere. To accomplish this we need an interior point x from which the projection can be made. This point must have the property that it can “see” every point in the polyhedron. For a convex polyhedron we can chose x to be any interior point. Most nonconvex polyhedra, however, have no such central point, but those that do are called star-convex. Kepler’s star polyhedra, shown in figure 6.6, are examples of star-convex polyhedra, as are the ones shown in figure 10.12. For each of these, there is an interior point that is “all seeing,” and from this point the projection can be made. Poinsot explained it as follows.

Figure 10.12. Star-convex polyhedra.

Figure 10.13. Louis Poinsot.
[Euler’s formula] still endures for any polyhedron with reentrant solid angles, provided that one can find, in the inside of the solid, a point which is the center of a sphere such that when the faces of the solid are cast there by lines that lead to the center, there is no duplication of these projections on the sphere; I mean to say, provided no face, in part or as a whole, is cast on the projection of another one; which applies, as one sees, for an infinite number of polyhedra with reentrant solid angles. One recognizes the truth of this proposition easily from the very proof of Mr. Legendre, in which there will be nothing to change.7
Thanks to Legendre, by the end of the nineteenth century Euler’s formula was put on sound footing for all convex polyhedra, and his popular textbook spread the beauty of Euler’s formula to a broad audience. In the years that followed, Poinsot and other important mathematicians became entranced by this elegant relation. They searched for new proofs and for further generalizations. To understand some of these generalizations, we need to investigate the field of graph theory. The origins of this field date back, not surprisingly, to Euler—and a recreational mathematics puzzle from the city of Königsberg.
* In everyday life we measure angles in degrees—a right angle is 90°, there are 360° in a circle, and so on. However, in most mathematical applications angles are measured in radians. The conversion is simple: 180° corresponds to π radians. So a right angle is π/2 radians and there are 2π radians in a full turn. We will see concrete examples later that illustrate why radians are superior to degrees.