Chapter 7
Clustering
Abstract
Clustering is an unsupervised data mining technique where the records in a data set are organized into different logical groupings. The groupings are in such a way that records inside the same group are more similar than records outside the group. Clustering has a wide variety of applications ranging from market segmentation to customer segmentation, electoral grouping, web analytics, and outlier detection. Clustering is also used as a data compression technique and data preprocessing technique for supervised data mining tasks. Many different data mining approaches are available to cluster the data and are developed based on proximity between the records, density in the data set, or novel application of neural networks. K-means clustering, density clustering, and self-organizing map techniques are reviewed in the chapter along with implementations using RapidMiner.
Keywords
Centriod; clustering; DBSCAN; density clustering; k-means clustering; Kohonen networks; Kohonen networks; self-organizing mapsClustering is the process of finding meaningful groups in data. In clustering, the objective is not to predict a target class variable, but to simply capture the possible natural groupings in the data. For example, customers of a company can be grouped based on the purchase behavior. In recent years, clustering has even found its use in political elections (Pearson & Cooper, 2012). Prospective electoral voters can be clustered into different groups so that candidates can tailor messages to resonate within each group. Before we proceed, we should further clarify the difference between classification and clustering using a simple example. Categorizing a given voter as a soccer mom (a known user group) or not is a supervised learning task of classification task. Segregating a population of electorates into different groups, based on similar demographics is an unsupervised learning task of clustering. The process of identifying whether a data point belongs to a particular known group is classification. The process of dividing data into meaningful groups is clustering.
In many cases one would not know ahead of what groups to look for and thus the identified groups might be difficult to explain. These identified groups are referred to as clusters. The data mining task of clustering can be used in two different classes of applications: to describe a given data set and as a preprocessing step for other predictive algorithms.
Clustering to Describe the Data
The most common application of clustering is to explore the data and find all possible meaningful groups in the data. Clustering a company’s customer records and attributes can yield a few groups in such a way that customers within a group are more like each other than customers belonging to a different group. Depending on the clustering technique used, the number of groups or clusters is either user defined or automatically determined by the algorithm. Since clustering is not about predicting the membership of a customer in a well-defined meaningful group (e.g., frequent high volume purchaser), we need to investigate carefully the similarities of customers within a group to make sense of the group as a whole. Some of the common applications of clustering to describe the underlying natural structure of the data are:
1. Marketing: Finding the common groups of customers based on all past customer behaviors, potential customers’ attributes, and/or purchase patterns. This task is helpful to segment the customers, identify prototype customers (description of a typical customer of a group), and tailor a marketing message to the customers in a group.
2. Document clustering: One of the common text mining task is to automatically group the documents (or text blobs) into groups of similar topics. Document clustering provides a way of identifying key topics, comprehend and summarize these clustered groups than reading through whole documents. Document clustering is used for routing customer support incidents, online content sites, forensic investigations, etc.
3. Session grouping: In web analytics, clustering is helpful to understand clusters of clickstream patterns and discover different kinds of clickstream profiles. One clickstream profile may be that of customers who knows what they want and proceed straight to checkout. Another profile may be that of customers that research the products, read through customer reviews, and make a purchase during a later sessions. Clustering the web sessions by profile helps an ecommerce company to provide features fitting each customer profile.
Clustering for Preprocessing
Since clustering processes consider all the attributes of the data set and “reduce” the information to a cluster, which is really another attribute (i.e. the ID of the cluster to which a record would belong to), clustering can be used as a data compression technique. The output of clustering is the cluster name for each record and can be used as an input variable for other predictive data mining tasks. Hence, clustering can be employed as a preprocessing technique for other data mining processes. In general, clustering can be used for two types of preprocessing:
1. Clustering to reduce dimensionality: In an n-dimensional data set (n number of attributes), the computational complexity is proportional to the number of dimensions or “n.” With clustering, n-dimensional attributes can be converted or reduced to one categorical attribute—“Cluster ID”. This reduces the complexity, although there will be some loss of information because of the dimensionality reduction to one single attribute. Chapter 12 Feature Selection provides an in-depth look at feature selection techniques.
2. Clustering for object reduction: Let’s assume that the number of customers for a company is in the millions and the number of cluster groups is 100. For each of these 100 cluster groups, we can identify one “poster child” customer that represents the characteristics of all the customers in the cluster group. The poster child customer can be an actual customer or a fictional customer with typical characteristics of customers in the group. The prototype of a cluster is the most common representation of all the data objects and it may be a new object whose attribute values are the average values of all objects within the cluster for each attribute (the most frequently occurring value in the case of categorical attributes). Reducing millions of customer records to 100 prototype records provides an obvious benefit. For a few applications, instead of processing millions of records, we can just process the prototypes for further classification or regression tasks. This greatly reduces the record object count and can be used in algorithms like k-NN where computation complexity depends on the number of records.
7.1. Types of Clustering Techniques
Regardless of the types of clustering applications, the data mining task of clustering seeks to find the groupings in data, in such a way that data points within a cluster are more “similar” to each other than to data points in other clusters (Witten & Frank, 2005). One of the common ways of measuring similarity is the Euclidean distance measurement in n-dimensional space which is used in many clustering algorithms. In Figure 7.1 all data points in Cluster 2 are closer to other data points in Cluster 2 than other data points in Cluster 1.
Before we get into different ways to implement clustering, we need to define the different types of clusters. Based on a data point’s membership to identified groups, clusters can be:
▪ Exclusive or strict partitioning clusters: Each data object belongs to one exclusive cluster, like the example shown in Figure 7.1. This is the most common type of cluster.
▪ Overlapping clusters: The cluster groups are not exclusive and each data object may belong to more than one cluster. These are also known as multiview clusters. For example, customers of a company can be grouped in a high-profit customer cluster and high-volume customer cluster at the same time.
▪ Fuzzy or probabilistic clusters: Each data point belongs to all cluster groups with varying degrees of membership from 0 to 1. For example, in a data set with clusters A, B, C, and D, a data point can be associated with all clusters with degree A = 0.5, B = 0.1, C = 0.4, and D = 0. Instead of a definite association of a data point with one cluster, fuzzy clustering associates a probability of membership to all the clusters.
Clustering techniques can also be classified based on the algorithmic approach used to find clusters in the data set. Each of these classes of clustering algorithms differ based on what relationship they leverage between the data objects.
▪ Prototype-based clustering: In prototype-based clustering, each cluster is represented by a central data object, also called a prototype. The prototype of each cluster is usually the center of the cluster, hence this clustering is also called centroid clustering or center-based clustering. For example, in clustering customer segments, each customer cluster will have a central prototype customer and customers with similar properties are associated with the prototype customer of a cluster.
▪ Density clustering: In Figure 7.1, we can observe that clusters occupy the area where there are more data points per unit space and are separated by sparse space. A cluster can also be defined as a dense region where data objects are concentrated surrounded by a low-density area where data objects are sparse. Each dense area can be assigned a cluster and the low-density area can be discarded as noise. In this form of clustering not all data objects are clustered since noise objects are unassigned to any clusters.
▪ Hierarchical clustering: Hierarchical clustering is a process where a cluster hierarchy is created based on the distance between data points. The output of a hierarchal clustering is a dendrogam: a tree diagram that shows different clusters at any point of precision which is specified by the user. There are two approaches to create a hierarchy of clusters. A bottom-up approach is where each data point is considered a cluster, and the clusters are merged to finally form one massive cluster. The top-down approach is where the data set is considered one cluster and they are recursively divided into different subclusters until individual data objects are defined as separate clusters. Hierarchical clustering is useful when the data size is limited. A level of interactive feedback is required to cut the dendrogam tree at a given level of precision.
▪ Model-based clustering: Model-based clustering gets its foundation from statistics and probability distribution models; this technique is also called distribution-based clustering. A cluster can be thought of as a grouping that has the data points belonging to the same probability distribution. Hence, each cluster can be represented by a distribution model (like Gaussian or Poisson), where the parameter of the distribution can be iteratively optimized between the cluster data and the model. With this approach, the entire data set can be represented by a mixture of distribution models. Mixture of Gaussians is one of the model-based clustering techniques used where a fixed number of distributions are initialized and parameters are optimized to fit the cluster data.
In the rest of the chapter, we will discuss common implementations of clustering. We will start with k-means clustering, which is a kind of prototype clustering technique. We will follow this with the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) which provides a view into density clustering, and we finish off with a novel approach called self-organizing maps (SOM).
7.2. k-Means Clustering
k-means clustering is a prototype-based clustering method where the data set is divided into k clusters. k-means clustering is one of the simplest and most commonly used clustering algorithms. In this technique, the user specifies the number of clusters (k) that need to be grouped in the data set. The objective of k-means clustering is to find a prototype data point for each cluster; all the data points are then assigned to the nearest prototype, which then forms a cluster. The prototype is called as the centroid, the center of the cluster. The center of the cluster can be the mean of all data objects in the cluster, as in k-means, or the most represented data object, as in k-medoid clustering. The cluster centroid or mean data object does not have to be a real data point in the data set and can be an imaginary data point that represents the characteristics of all data points within the cluster.
The k-means clustering algorithm is based on the works of Stuart Lloyd and E.W. Forgy (Lloyd, 1982) and is sometimes referred to as the Lloyd-Forgy algorithm or Lloyd’s algorithm. Visually, the k-means algorithm divides the data space into k partitions or boundaries, where the centroid in each partition is the prototype of the clusters. The data objects inside a partition belong to the cluster. These partitions are also called Voronoi partitions, and each prototype is a seed in a Voronoi partition. A Voronoi partition is a process of segmenting a space into regions, around a set of points called seeds. All other points are then associated to the nearest seed and the points associated with the seed form a unique partition. Figure 7.2 shows a sample Voronoi partition around seeds marked as black dots.
k-means clustering creates k partitions in n-dimensional space, where n is the number of attributes in data sets. To partition the data set we would need to define a proximity measure. The most commonly used measure for a numeric attribute is the Euclidean distance. Figure 7.3 illustrates the clustering of the Iris data set with only the petal length and petal width attributes. This Iris data set is two dimensional, with numeric attributes and k specified as 3. The outcome of k-means clustering provides a clear partition space for Cluster 1 and a narrow space for the other two clusters, Cluster 2 and Cluster 3.
7.2.1. How it Works: Concepts
The logic of finding k-clusters with a given data set is rather simple and always converges to a solution. However, the final result in most cases will be locally optimal where the solution will not converge to the global best solution. The process of k-means clustering is very similar to Voronoi iteration, where the objective is to divide a space into cells around points. The difference is Voronoi iteration partitions space, whereas k-means clustering partitions data points in data space. Let’s take the example of a two-dimensional data set (Figure 7.4) and walk through the step-by-step process of finding three clusters (Tan, Michael, & Kumar, 2005).
Step 1: Initiate Centroids
The first step in a k-means algorithm is to initiate k random centroids. The number of clusters k should be specified by the user. In this case we initiate three centroids in a given data space. In Figure 7.5, each initial centroid is given a shape (with a circle to differentiate centroids from other data points) so that data points assigned to a centroid can be indicated by same shape.
Step 2: Assign Data Points
Once centroids have been initiated, all the data points are now assigned to the nearest centroid to form a cluster. In this context the “nearest” is calculated by a proximity measure. Euclidean distance measurement is the most common proximity measure, though other measures like the Manhattan measure and Jaccard coefficient can be used. The Euclidean distance between two data points X (x1, x2,…xn) and C (c1, c2,…cn) with n attributes is given by
(7.1)
All the data points associated to a centroid now have the same shape as their corresponding centroid as shown in Figure 7.6. This step also leads to partitioning of data space into Voronoi partitions, with lines shown as boundaries.
Step 3: Calculate New Centroids
For each cluster, we can now calculate a new centroid, which is also the prototype of each cluster group. This new centroid is the most representative data point of all data points in the cluster. Mathematically, this step can be expressed as minimizing the sum of squared errors (SSE) of all data points in a cluster to the centroid of the cluster. The overall objective of the step is to minimize the sum of squared errors of individual clusters. The SSE of a cluster can be calculated by Equation 7.2.
(7.2)where 
is the ith cluster, j are the data points in a given cluster, 
is the centroid for ith cluster, and 
is a specific data object. The centroid with minimal SSE for the given cluster i is the new mean of the cluster. The mean of the cluster can be calculated by
is the ith cluster, j are the data points in a given cluster, is the centroid for ith cluster, and is a specific data object. The centroid with minimal SSE for the given cluster i is the new mean of the cluster. The mean of the cluster can be calculated by
(7.3)where X is the data object vector (x1, x2,… xn). In the case of k-means clustering, the new centroid will be the mean of all the data points k-medoid clustering is a variation of k-means clustering, where the median is calculated instead of mean. Figure 7.7 shows the location of the new centroids.
Step 4: Repeat Assignment and Calculate New Centroids
Once the new centroids have been identified, assigning data points to the nearest centroid is repeated until all the data points are reassigned to new centroids. In Figure 7.8, note the change in assignment of two data points that belonged to different clusters in the previous step.
Step 5: Termination
Step 3, calculating new centroids, and step 4, assigning data points to new centroids, are iterative until no further change in assignment of data points happens or, in other words, no significant change in centroids are noted. The final centroids are declared the prototype data objects or vectors and they are used to describe the whole clustering model. Each data point in the data set is now tied with a new clustering ID attribute that identifies the cluster.
Special Cases
Even though k-means clustering is simple and easy to implement, one of the key drawbacks of k-means clustering is the algorithm seeks to find a local optimum, which may not yield globally optimal clustering. In this approach, the algorithm starts with an initial configuration (centroids) and continuously improves to find the best solution possible for that initial configuration. Since the solution is optimal to the initial configuration (locally optimal), there might be a better optimal solution if the initial configuration changes. The locally optimal solution may not be the most optimal solution (globally optimal) for the given clustering problem. Hence, the success of a k-means algorithm very much depends on the initiation of centroids. This limitation can be addressed by having multiple random initiations; in each run we can measure the cohesiveness of the clusters by a performance criterion. The clustering run with the best performance can be chosen as the final run. Evaluation of clustering is discussed in next section. Following are key issues to be considered in k-means clustering:
▪ Initiation: The final clustering grouping depends on the random initiator and the nature of the data set. When random initiation is used, we can run the entire clustering process (also called “runs”) with a different set of random initiators and find the clustering process that has minimal total SSE. Another technique is hierarchical clustering, where each cluster is in turn split into multiple clusters and thereby minimal SSE is achieved. Hierarchical clustering is further divided into agglomerative or bottom-up clustering and divisive or top-down clustering, depending on how the clustering is initiated. Agglomerative clustering starts with each data point as an individual cluster and proceeds to combine data points into clusters. Divisive clustering starts with the whole data set as one big cluster and proceeds to split that into multiple clusters.
▪ Empty clusters: One of the possibilities in k-means clustering is the formation of empty clusters in which no data objects are associated. If empty clusters are formed, a new centroid can be introduced in the cluster that has the highest SSE, thereby splitting the cluster that contributes to the highest SSE or selecting a new centroid that is at the farthest point away from any other centroid.
▪ Outliers: Since SSE is used as an objective function, k-means clustering is susceptible to outliers; they drift the centroid away from the representative data points in a cluster. Hence the prototype is no longer the best representative of the clusters it represents. While outliers can be eliminated by preprocessing techniques, in some applications finding outliers or a group of outliers is the objective of clustering, similar to identifying fraudulent transactions.
▪ Postprocessing: Since k-means clustering seeks to be locally optimal, we can introduce a few postprocessing techniques to force a new solution that has less SSE. We always can increase the number of clusters, k, and reduce SSE. But, this technique can start overfitting the data set and yields less useful information. There are a few approaches that can be deployed, such as bisecting the cluster that has highest SSE and merging two clusters into one even if SSE increases slightly.
Evaluation of Clusters
Evaluation of k-means clustering is different from regression and classification algorithms because in clustering there are no known external labels for comparison. We will have to develop the evaluation parameter from the very data set that is evaluated. This is called unsupervised or internal evaluation. Evaluation of clustering can be as simple as computing total SSE. Good models will have low SSE within the cluster and low overall SSE among all clusters. SSE can also be referred to as the average within-cluster distance and can be calculated for each cluster and then averaged for all the clusters.
Another commonly used evaluation measure is the Davies-Bouldin index (Davies & Bouldin, 1979). The Davies-Bouldin index is a measure of uniqueness of the clusters and takes into consideration both cohesiveness of the cluster (distance between the data points and center of the cluster) and separation between the clusters. It is the function of the ratio of within cluster separation to the separation between the clusters. The lower the value of the Davies-Bouldin index, the better the clustering. However, both SSE and the Davies-Bouldin index have the limitation of not guaranteeing better clustering when they have lower scores.
7.2.2. How to Implement
k-means clustering implementation in RapidMiner is simple and straightforward with one operator for modeling and one for unsupervised evaluation. In the modeling step, the parameter for the number of clusters, k, is specified as desired. The output model is a list of centroids for each cluster and a new attribute is attached to the original input data set with the cluster ID. The cluster label is appended to the original data set for each data point and can be visually evaluated after the clustering. A model evaluation step is required to calculate the average cluster distance and Davies-Bouldin index.
For this implementation, we are using the Iris data set with four attributes and 150 data objects (Fisher, 1936). Even though a class label is not needed for clustering, we choose to keep it for later explanation to see if identified clusters from an unlabeled data set are similar to natural clusters of species in the given data set.
Step 1: Data Preparation
k-means clustering accepts both numeric and polynominal data types; however, the distance measures are more effective with numeric data types. The number of attributes increases the dimension space for clustering. In this example we limit the number of attributes to two by selecting petal width (a3) and petal length (a4) using the Select attribute operator as shown in Figure 7.9. It is easy to visualize the mechanics of k-means algorithm by looking at two-dimensional plots for clustering. In practical implementations, clustering data sets will have more attributes.
Step 2: Clustering Operator and Parameters
The k-means modeling operator is available in Modeling > Clustering and Segmentation folder of RapidMiner. The following parameters can be configured in the model operator:
▪ k: k is the desired number of clusters.
▪ Add cluster as attribute: Append cluster labels (IDs) into the original data set. Turning on this option is recommended for later analysis.
▪ Max runs: Since the effectiveness of k-means clustering is dependent on random initial centroids, multiple runs are required to select the clustering with the lowest SSE. The number of such runs can be specified here.
▪ Measure type: The proximity measure can be specified in this parameter. The default and most common measurement is Euclidean distance (L2). Other options here are Manhattan distance (L1), Jaccard coefficient, and cosine similarity for document data. Please refer to Chapter 4 Classification section k-NN for description on distance measures.
▪ Max optimization steps: This parameter specifies the number of iterations of assigning data objects to centroids and calculating new centroids.
The output of the modeling step includes the cluster model with k centroid data objects and the initial data set appended with cluster labels. Cluster labels are named generically such as cluster_0, cluster_1,…, cluster_k–1.
Step 3: Evaluation
Since the attributes used in the data set are numeric, we need to evaluate the effectiveness of clustering groups using SSE and the Davies-Bouldin index. In RapidMiner, the Cluster Distance Performance operator under Evaluation > Clustering is available for performance evaluation of cluster groups. Performance operator needs accepts both inputs from the modeling step: cluster centroid vector (model) and the labeled data set. The two measurement outputs of the evaluation are average cluster distance and the Davies-Bouldin index.
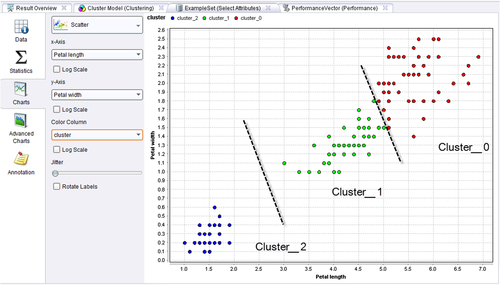
Step 4: Execution and Interpretation
After the outputs from the performance operator have been connected to the result ports, the data mining process can be executed. The following outputs can be observed from results window:
▪ Cluster Model (Clustering): The model output contains the centroid for each of the k clusters, along with their attribute values. As shown in Figure 7.10, in the text view and folder view sections, we can see all the data objects associated with the each cluster. The centroid plot view provides the parallel chart view (Chapter 3 Data Exploration) of centroids. A large separation between centroids is desirable, because well-separated clusters divide the data set cleanly.
▪ Labeled example set: The appended data set has some of the most important information on clustering. The generic Iris data set of 150 observations is clustered in three groups. The cluster value is appended as a new special polynominal attribute and takes a generic label format. In the scatterplot view of this output data set, we can configure the x- and y-axes to be attributes of original data set, petal length and petal width. The Color Column can be configured for cluster labels. In the plot in Figure 7.11, we notice how the algorithm identified clusters. We can compare this output against the original label (Iris species) by swapping the Color Column to the species label. Here we can observe that only five data points in the border of versicolor and virginica are mis-clustered! The k-means clustering process identified the different species in the data set almost exactly.
▪ Performance vector: The output of the performance evaluation includes the average distance measured and the Davies-Bouldin index (Figure 7.12). This step can be used to compare multiple clustering processes with different parameters. In advanced implementations, it is possible to determine the value of k based on the clustering runs with the best performance vectors. Amongst multiple clustering runs, the low average-within-centroid distance and low Davies-Bouldin index yields better clusters, because they indicate the cohesiveness of the cluster.
The k-means clustering algorithm is simple, easy to implement, and easy to interpret. Although the algorithm can effectively handle an n-dimensional data set, the operation will be expensive with a higher number of iterations and runs. One of the key limitations of k-means is that it relies on the user to assign the value of k (Berry & Linoff, 2000). The number of clusters in the data set will be unknown to begin with and an arbitrary number can limit the ability to find the right number of natural clusters in the data set. There are a variety of methods to estimate the right number for k, ranging from the Bayesian Information Criterion (BIC) to hierarchical methods that increases the value of k until the data points assigned to the cluster are Gaussian (Hamerly & Elkan, 2003). For a start, we recommend a value of k in the low single digits and increasing it until it fits. Clustering using density methods will help provide an idea into the number of clusters and could be used as a value of k in k-means clustering.
Since the centroid prototype approach is used, k-means tends to find globular clusters in the data set. However, natural clusters can be of all shapes and sizes. The presence of outliers possesses a challenge in the modeling of k-means clustering. The simplicity of the k-means clustering technique makes it a great choice for quick evaluation of globular clusters and as a preprocessing technique for predictive modeling and for dimensionality reduction.
7.3. DBSCAN Clustering
A cluster can also be defined as an area of high concentration (or density) of data objects surrounded by areas of low concentration (or density) of data objects. A density-clustering algorithm identifies clusters in the data based on measurement of the density distribution in n-dimensional space. Unlike centroid methods, specifying the number of the cluster parameter (k) is not necessary for density-based algorithms. Thus density-based clustering can serve as an important data exploration technique. DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is one of the most commonly used density-clustering algorithms (Ester et al.,1996). To understand how the algorithm works, we need to first define the concept of density in a data space.
Density can be defined as the number of data points in a unit n-dimensional space. The number of dimensions n is the number of attributes in a data set. To simplify the visualization and to further understand how the model works, let’s consider a two-dimensional space or a data set with two numeric attributes. From looking at the data set represented in Figure 7.13, we can visually conclude that density in the top-left section is higher than density in top-right, bottom-left, and bottom-right sections. Technically, density relates to the number of points in unit space, in this case a quadrant. Wherever there is high-density space amongst relatively low-density spaces, there is a cluster.
We can also measure density within a circular space around a point as in Figure 7.14. The number of points within a circular space with radius ε (epsilon) around a data point A is six. This measure is called center-based density since the space considered is globular with the center being the point that is considered.
7.3.1. How it Works
The DBSCAN algorithm creates clusters by identifying high-density and low-density space within the data set. Similar to k-means clustering, it is preferred that the attributes are numeric because distance calculation is still used. We can reduce the algorithm to three steps: defining threshold density, classification of data points, and clustering (Tan, Michael, & Kumar, 2005).
Step 1: Defining Epsilon and MinPoints
The DBSCAN algorithm starts with calculation of a density for all data points in a data set, with a given fixed radius ε (epsilon). To determine whether a neighborhood is high density or low density, we will have to define a threshold of data points (MinPoints) above which the neighborhood is considered high density. In Figure 7.14, the number of data points inside the space is defined by radius ε. If MinPoints is defined as 5, the space ε surrounding data point A is considered a high-density region. Both ε and MinPoints are user-defined parameters and can be altered for a data set.
Step 2: Classification of Data Points
In a data set, with a given ε and MinPoints, we can classify all data points into three buckets (Figure 7.15):
▪ Core points: All the data points inside the high-density region of at least one data point are considered a core point. A high-density region is a space where there are at least MinPoints data points within a radius of ε for any data points.
▪ Border point: Border points sit on the circumference of radius ε from a data point. A border point is the boundary between high-density and low-density space. Border points are counted within the high-density space calculation.
Step 3: Clustering
Once all data points in the data set are classified into density points, clustering is a straightforward task. Groups of core points form distinct clusters. If two core points are within ε of each other, then both core points are within the same cluster. All these clustered core points form a cluster, which is surrounded by low-density noise points. All noise points form low-density regions around the high-density cluster, and noise points are not classified in any cluster. Since DBSCAN is a partial clustering algorithm, a few data points are left unlabeled or associated to a default noise cluster.
Optimizing Parameters
One of the key advantages in using a density algorithm is that there is no need for specifying the number of clusters (k). Clusters are automatically found in the data set. However, there is an issue of selecting the distance parameter ε and a minimum threshold (MinPoints) to identify the dense region. One of the techniques used to estimate optimal parameters for the DBSCAN clustering algorithm relates to the k-nearest neighbor algorithm. We can estimate the initial values of the parameter by building a k-distribution graph. For a user-specified value of k (say, four data points), we can calculate the distance of the k-th nearest neighbor for a data point. If the data point is a core point in a high-density region, then the distance of the k-th nearest neighbor will be smaller. For a noise point, the distance will be larger. Similarly, we can calculate the k-distance for all data points in a data set. A k-distance distribution graph can be built by arranging all the k-distance values of individual data points in descending order, as shown in Figure 7.16. This arrangement is similar to Pareto charts. Points on the right-hand side of the chart will belong to data points inside a cluster, because the distance is smaller. In most data sets, the value of k-distance sharply rises after a particular value. The distance at which the chart rises will be the optimal value ε (epsilon) and the value of k can be used for MinPoints.
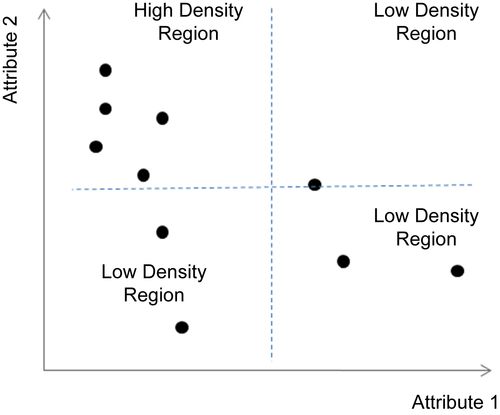
Special Cases: Varying Densities
The DBSCAN algorithm partitions data based on a certain threshold density. This approach creates an issue when a data set contains areas of varying data density. The data set in Figure 7.17 has four distinct regions numbered from 1 to 4. Region 1 is the high-density area A, regions 2 and 4 are of medium density B, and between them is region 3, which has very low density C. If the density threshold parameters are tuned in such a way to partition and identify region 1, then region 2 and 4 (with density B) will be considered noise, along with region 3. Even though region 4 with density B is next to a very-low-density area and clearly identifiable visually, the DBSCAN algorithm will classify regions 2 through 4 as noise. The k-means clustering algorithm is better at partitioning data sets with varying densities.
7.3.2. How to Implement
The implementation of the DBSCAN algorithm is supported in RapidMiner through the DBSCAN modeling operator. The DBSCAN operator accepts numeric and polynominal data set with provisions for user-specified ε (epsilon) and MinPoints parameters. Here are the implementation steps.
Step 1: Data Preparation
As with the k-means section, we will limit the number of attributes in the data set to A3 and A4 (petal length and petal width) using the Select Attribute operator, so that we can visualize the cluster and better understand the clustering process.
Step 2: Clustering Operator and Parameters
The modeling operator is available in the Modeling > Clustering and Segmentation folder, and is labeled DBSCAN. The ollowing parameters can be configured in the model operator:
▪ Epsilon (ε): Size of the high-density neighborhood. The default value is 1.
▪ MinPoints: Minimum number of data objects within the epsilon neighborhood to qualify as a cluster.
▪ Distance measure: The proximity measure can be specified in this parameter. The default and most common measurement is Euclidean distance. Other options here are Manhattan distance, Jaccard coefficient, and cosine similarity for document data. Please refer to Figure 4.32 for a summary of different distance measures.
▪ Add cluster as attributes: To append cluster labels into the original data set. Turing on this option is recommended for later analysis.
Step 3: Evaluation (Optimal)
Similar to k-means clustering implementation, we can evaluate the effectiveness of clustering groups using average within cluster distance. In RapidMiner, the Cluster Density Performance operator under Evaluation > Clustering is available for performance evaluation of cluster groups generated by Density algorithms. The clustering model and labeled data set is connected to performance operator for cluster evaluation. Additionally, to aid the calculation, performance operator expects Similarity Measure object. A similarity measure vector is a distance measure of every example data object with the other data object. The similarity measure can be calculated by using Data to Similarity Operator on the example data set.
Step 4: Execution and Interpretation
After the outputs from the performance operator have been connected to the result ports, as shown in Figure 7.18, the model can be executed. The following result output can be observed.
1. Model: The cluster model output contains information on the number or clusters found in the data set (Cluster 1, Cluster 2, …) and data objects identified as noise points (Cluster 0). If no noise points are found, then Cluster 0 is an empty cluster. As shown in Figure 7.19, the Folder view and Graph view from the output window provide the visualization of data points classified under different clusters.
2. Clustered example set: The example set now has a clustering label that can be used for further analysis and visualization. In the scatterplot view of this data set (Figure 7.20), we can configure the x- and y-axes to be attributes of the original data set, petal length and petal width. The Color Column can be configured to be the new cluster label. In the plot, we notice how the algorithm found two clusters within the example set. The setosa species data objects have clear high-density areas but there is a density bridge between the verisicolor and virginica species data points. There is no clear low-density area to partition these two species of data points. Hence verisicolor and virginica natural clusters are combined to one artificial predicted cluster. The epsilon and MinPoints parameters can be adjusted to find different results for the clustering.
3. Performance vector: The performance vector window shows average distance within each cluster and average of all clusters. The average distance is the distance between all the data points within the cluster divided by number of data points. These measures can be used to compare the performance of multiple model runs.
7.3.3. Conclusion
The main attraction of using DBSCAN clustering is that we do not have to specify the value of k, the number of clusters to be identified. In many practical applications, the number of clusters to be discovered will be unknown, like finding unique customers or electoral segments. DBSCAN uses variations in the density of the data distribution to find the concentration of structures in data. These clusters can be of any shape and they are not confined to globular structures as in the k-means approach. But the density algorithms run into the risk of finding bridges between two natural clusters and merging them into one cluster.
Since the density clustering technique yields partial clustering, DBSCAN ignores noise and outlier data points and they are not clustered in final results. The inability to identify varying densities within a data set is one of the major limitations of DBSCAN clustering technique. Centroid methods are more successful at finding varying density patterns in the data set. A data set with a high number of attributes will have processing challenges with density clustering methods. Given the complementary pros and cons of the k-means and DBSCAN methods, it is advisable to cluster the data set by both methods and understand the patterns of both result sets.
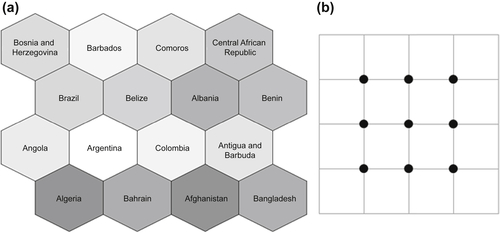
7.4. Self-Organizing Maps
A self-organizing map (SOM) is a powerful visual clustering technique that evolved from the combination of neural networks and prototype-based clustering. A SOM is a form of neural network where the output is an organized visual matrix, usually a two-dimensional grid with rows and columns. The objective of this neural network is to transfer all input data objects with n attributes (n dimensions) to the output lattice in such a way that objects next to each other are closely related to each other. Two example SOM layouts are provided in Figure 7.21. This two-dimensional matrix becomes an exploration tool in identifying the clusters of objects related to each other by visual examination. A key distinction in this neural network is the absence of an output target function to optimize or predict, hence it is an unsupervised learning algorithm. SOMs effectively arrange the data points in a lower dimensional space, thereby aids visualizing high-dimensional data through a low-dimensional space.
SOMs are relevant to clustering because the most common SOM output is a two-dimensional grid with data objects placed next to each other based on their similarity to one another. Objects related to each other are placed in close proximity. SOMs differ from other clustering techniques because there is no explicit clustering labels assigned to data objects. Data objects are arranged based on their attribute proximity and the task of clustering is left to visual analysis of the user. Hence, SOM is used as a visual clustering and data exploration technique (Germano, 1999).
Self-organizing maps were first proposed by Teuvo Kohonen (Kohonen, 1982) and hence this technique is also known as Kohonen networks; it is sometimes also referred to by a more specific name, self-organizing feature maps. SOM methodology is used to project data objects from data space, mostly in n dimensions, to grid space, usually resulting in two dimensions. Though other output formats are possible, most common output format for SOMs are (a) hexagonal lattice or a (b) rectangular grid as shown in Figure 7.21. Each data point from the data set occupies a cell or a node in the output lattice, with arrangement constraints depending on the similarity of data points. Each cell in the SOM grid corresponds to a group of data points, called a neuron. In a hexagonal grid, each neuron has six neighbors and a rectangular lattice has four neighbors.
SOMs are commonly used in comparing data points with a large number of numeric attributes. The objective of this kind of analysis is to compare the relative features of data objects in a simple two-dimensional setting where the placement of objects is related to each other. In Figure 7.21a, the SOM compares relative GDP data from different countries where countries with similar GDP profiles are placed either in same cells or next to each other. All similar countries around a particular cell can be considered a grouping. Although the individual data objects (countries) do not have a cluster membership, the placement of objects together aides in visual data analysis. This application is also called competitive self-organizing maps.
7.4.1. How it Works: Concepts
The algorithm for a SOM is similar to centroid-based clustering but with a neural network foundation. Since a SOM is essentially a neural network, the model accepts only numerical attributes. However, there is no target variable in SOM because it is an unsupervised learning model. The objective of the algorithm is to find a set of centroids (neurons) to represent the cluster but with topological constraints. The topology refers to an arrangement of centroids in the output grid. All the data objects from the data set are assigned to each centroid. Centroids closer to each other in the grid are more closely “related” to each other than to centroids further away in the grid. A SOM converts numbers from the data space to a grid space with additional inter-topology relationships.
Step 1: Topology Specification
The first step for a SOM is specifying the topology of the output. Even though multidimensional output is possible, two-dimensional rows and columns with either a rectangular lattice or hexagonal lattice are commonly used in SOMs to aid the visual discovery of clustering. One advantage in using a hexagonal lattice is that each node or centroid can have six neighbors, two more than in a rectangular lattice. Hence, in a hexagonal lattice, the association of a data point with another data point can be more precise than for a rectangular grid. The number of centroids can be specified by providing the number of rows and columns in the grid. The number of centroids is the product of the number of rows and columns in the grid. Figure 7.22 shows the hexagonal lattice SOM.
Step 2: Initialize Centroids
A SOM starts the process by initializing the centroids. The initial centroids are values of random data objects from the data set. This is similar to initializing centroids in k-means clustering.
Step 3: Assignment of Data Objects
After centroids are selected and placed on the grid in the intersection of rows and columns, data objects are selected one by one and assigned to the nearest centroid. The nearest centroid can be calculated using a distance function like Euclidean distance for numeric data or a cosine measure for document or binary data. Section 4.3.1 provides a summary of distance and similarity measures.
Step 4: Centroid Update
The centroid update is the most significant and distinct step in the SOM algorithm and is repeated for every data object. The centroid update has two related substeps.
The first substep is to update the closest centroid. The objective of the method is to update the data values of the nearest centroid of the data object, proportional to the difference between the centroid and the data object. This is similar to updating weights in the back propagation algorithm of neural networks. In the neural network section of Chapter 4 Classification, we discussed how the weights of neurons are updated based on the error difference between the predicted and actual value. Similarly, in the context of a SOM, the values of centroids are updated. In fact, centroids are considered neurons in a SOM. Through this update, the closest centroid moves closer to the data object in the data space.
The centroid update step is repeated for number of iterations, usually in the thousands. Let’s denote t as the tth iteration of the update where we pick the data point d(t). Let w1, w2, w3, …, wk represent all the centroids in the grid space. Figure 7.22 shows the lattice with centroid weight. Let r and c be the number of rows and columns in the grid. Then k will be equal to r ∗ c. Let wi be the nearest centroid for data object d(t). During iteration t, the nearest centroid wi is updated by Equation 7.4.
(7.4)The effect of the update is determined by the difference between the centroid and data point in the data space and the neighborhood function 
. The neighborhood function decreases for every iteration so there are no drastic changes made in the final iteration. In addition to updating the nearest primary centroid, all other centroids in the grid space neighborhood of the primary centroid are updated as well. We will review this in more detail in the next substep.
. The neighborhood function decreases for every iteration so there are no drastic changes made in the final iteration. In addition to updating the nearest primary centroid, all other centroids in the grid space neighborhood of the primary centroid are updated as well. We will review this in more detail in the next substep.The second substep is to update all centroids in the grid space neighborhood as shown in Figure 7.23. The neighborhood update step has to be proportional to the distance from the closest centroid to the centroid that is being updated. The update function has to be stronger when the distance is closer. Taking into account time decay and distance between neighborhood centroids, a Gaussian function is commonly used for 
:
:
(7.5)
Where 
is the learning rate function that takes a value between 0 and 1 and decays for every iteration. Usually it is either a linear rate function or an inverse of the time function. The variable in the exponential parameter 
is the distance between the centroid being updated and the nearest centroid of the data point in the grid space.
is the learning rate function that takes a value between 0 and 1 and decays for every iteration. Usually it is either a linear rate function or an inverse of the time function. The variable in the exponential parameter is the distance between the centroid being updated and the nearest centroid of the data point in the grid space.The variable σ determines the radius of the centroid update or the neighborhood effect. By updating the entire neighborhood of centroids in the grid, the SOM self-organizes the centroid lattice. Effectively, the SOM converts data from the data space to a location-constrained grid space.
Step 5: Termination
The entire algorithm is continued until no significant centroid updates take place in each run or until the specified number of the run counter is reached. The selection of the data object can be repeated if the data set size is small. Like with many data mining algorithms, a SOM tends to converge to a solution in most cases but doesn’t guarantee an optimal solution. To tackle this problem, it is necessary to have multiple runs with various initiation measures and compare the results.
Step 6: Mapping a New Data Object
A SOM model itself is a valuable visualization tool that can describe the relationship between data objects and be used for visual clustering. After the grids with the desired number of centroids have been built, any new data object can be quickly given a location on the grid space, based on its proximity to the centroids. The characteristics of new data objects can be further understood by studying the neighbors.
7.4.2. How to Implement
SOM can be implemented in a few different ways in RapidMiner, with varied functionality and resulting output.
▪ Data exploration chart: In Chapter 3 Data Exploration, we reviewed the SOM chart as one of the data exploration techniques. In RapidMiner, any data set connected to a result port has a SOM chart feature under the Chart tab. This is a quick and easy method where the number of rows and columns can be specified and a SOM chart can be rendered.
▪ Data Transformation > Attribute set reduction > SOM Operator: The SOM operator available under the Data Transformation folder is used to reduce the number of dimensions in the data set. It is similar to the application of principal component analysis (Chapter 12 Feature Selection) where the data set is reduced to a lower dimensionality. In theory, a SOM can help reduce the data to any number of dimensions below the dimension count of the data set. In this operator, the number of desired output dimensions can be specified in the parameters, as shown in Figure 7.24. The net size parameter indicates the unique values in each of the SOM dimensions. There is no visual output for this operator and in two dimensions, only a square topography can be achieved through the SOM data transformation operator.
▪ RapidMiner Extension > SOM Modeling Operator: The SOM modeling operator is available in the SOM extension (Motl, 2012) and offers rich SOM visuals. We will be using SOM extensions for the rest of this implementation section, so readers are encouraged to install the SOM extension before proceeding further.
The data set we use in this section is the relative gross domestic product (GDP) information by country (IMF, 2012) from the World Economic Outlook Database October 2012 by the International Monetary Fund. The data set has 186 records, one for each country, and four attributes in percentage of GDP: relative GDP invested, relative GDP saved, government revenue, and current account balance. Figure 7.25 shows the actual raw data for a few rows and Figure 7.26 shows the quartile plot for all the attributes.
The objective of the clustering is that we want to compare and contrast countries based on their percentage of GDP invested and saved, government revenue, and current account balance. Note that we are not comparing the size of the economy through absolute GDP but size of investment, national savings, current account, and size of government relative to the country’s GDP. The goal of this modeling exercise is to arrange countries in a grid so that countries with similar characteristics of investing, savings, size of government, and current account are placed next to each other. We are compressing four-dimensional information to a two-dimensional map or grid. The data set and RapidMiner process can be accessed from the companion site of the book at www.LearnPredictiveAnalytics.com.
Step 1: Data Preparation
As a neural network, a SOM cannot accept polynominal or categorical attributes because centroid updates and distance calculations work only with numeric values. Polynominal data can be either ignored with information loss or converted to a numeric attribute using the Nominal to Numerical type conversion operator available in RapidMiner. In the Country-GDP data set, there are records (each record is a country) where there is no data. Neural networks cannot handle missing values and hence it needs to be replaced by either zero or the minimum or average value for the attribute using the Replace Missing Value operator. In this example we choose the average as the default missing value.
Step 2: SOM Modeling Operator and Parameters
The SOM modeling extension operator is available in the Self-Organizing Map folder, labeled with the same name. Please note that SOM folder is visible only when SOM extension is installed. The following parameters can be configured in the model operator. The modeling operator accepts the example set with numeric data and a label attribute if applicable. In this example set, the country name is a label attribute. Figure 7.27 shows the RapidMiner process for developing a SOM model.
▪ Training Rounds: Defaults to 1000. This value indicates the number of training rounds for the data object selection process.
▪ Net Size: Indicates whether the grid size should be specified by the user or automatically approximated by the system. In this exercise we select user input for X and Y.
▪ Net Size X: Specifies the number of columns in the grid (horizontal direction). This is the same as the possible values for the SOM_0 attribute in the output. In this example we will set this value to 10.
▪ Learning Rate: The neural network learning parameter (λ), which takes a value from 0 to 1. The value of λ determines how sensitive the change in weight is to the previous weights. A value closer to 0 means the new weight would be more based on previous weight and an λ closer to 1 means that weight would be mainly based on error correction. We are assigning the initial λ is 0.9 (see Chapter 4 Classification and Section 4.5 on Neural Networks).
▪ Learning Rate function: The learning rate function in a neural network is a time decay function of the learning process. The default and most commonly used time decay function is the inverse of time.
Step 3: Execution and Interpretation
The RapidMiner process can be saved and executed. The output of the SOM modeling operator consists of a visual model and a grid data set. The visual model is a lattice with centroids and mapped data points. The grid data set output is the example set labeled with location coordinates for each record in the grid lattice.
Visual Model
The visual model of the SOM displays the most recognizable form of SOM in a hexagonal grid format. The size of the grid is configured by the input parameters that set the net size of X and Y. There are several advanced visualization styles available in Visualization results window. The SOM visual output can be customized by the following parameters:
▪ Visualization Style: This selection controls the visual layout and background color of the SOM hexagons. The value of the selected measure is represented as a background gradient color. The default, U-Matrix, presents a background gradient color proportional to the distance of the central data points in adjacent hexagons. The P-Matrix option shows the number of example data points through the background gradient color. The selection of an individual attribute name for the visualization style renders the background gradient proportional to the value of the selected attribute. The visualization style selection does not rearrange the data points assigned to hexagons.
▪ Label: Selection shows the attribute value selected in the hexagons.
▪ Color Schema: Selection of monochrome or color scheme.
Figure 7.28 shows a SOM with the default selection of the label as Country and the visualization style as U-Matrix. We can observe how countries are placed on the grid based on their relationship with each other, as evaluated by the four economic metrics in relation with GDP. Countries with similar characteristics are placed closer to each other than others in the grid. If more than one country belongs to a centroid (hexagon), then the label of one country closer to centroid is displayed on the grid. The grid locations of all the counties are listed in the location coordinates section of the results window.
A few interesting patterns in the data can be observed by changing the visualization style as a metric in the data set. In Figure 7.29, government revenue as percentage of GDP is used and visually, countries with high government revenue as a percentage of GDP is displayed on the top-left side of the grid (example: Belgium 48%) and countries with low government revenue are at bottom of the grid (Bangladesh 11%).
Figure 7.30 shows the national savings rate visualization to in the SOM; countries with a high savings rate (Algeria 49%) are concentrated on the left side and countries with a low savings rate (Maldives –2%) are concentrated on the right side of the SOM.
Location Coordinates
The second output of the SOM operator contains the location coordinates of the X- and Y-axes of grid with labels SOM_0 and SOM_1. The coordinate values of location range from 0 to net size – 1, as specified in the model parameters, since all data objects, in this case countries, are assigned to a specific location in the grid. This output, as shown in Figure 7.31, can be further used for postprocessing such as distance calculation of locations between countries in the grid space.
7.4.3. Conclusion
The methodology of self-organizing maps is derived from the foundations of both neural network and prototype-clustering approaches. Self-organizing maps are an effective visual clustering tool to understand numeric high-dimensional data. They reduce the features of the data set to two or three features, which is used to specify the topology of the layout. Hence, SOMs are predominantly used as a visual discovery and data exploration technique. Some of the recent applications of SOMs include the methods that are used in conjunction with other data mining and analytics techniques. SOMs are used in combination with graph mining (Resta, 2012), text mining (Liu et al., 2012), speech recognition (Kohonen, 1988), etc.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.