12

Different, yet the Same

The two theorems we just met—numbers 35 and 36 in book III of Euclid—sound strikingly similar: both are about a circle, a point P, and a line through P that cuts the circle at points R and S. The two theorems state that the product remains constant for all possible lines through P. Yet there is a difference: in theorem 35 P is inside the circle, while in theorem 36 it is outside. And theorem 36 has the additional result that , where is the length of the tangent line from P to the circle. So despite their similarity, they are two distinct statements, and Euclid was careful to list them as separate theorems, one following the other.

And yet a closer inspection will show that the two theorems are one and the same after all. For when we say that a point P is given with respect to a circle, we imply only that the distance from P to the center of the circle O is given, and nothing else. The actual position of P relative to the circle (that is, its direction from O) is immaterial. And since all points P with the same distance from O describe a second circle concentric to the given circle and having the radius , we conclude that has the same value for all points on this second, “implied” circle.

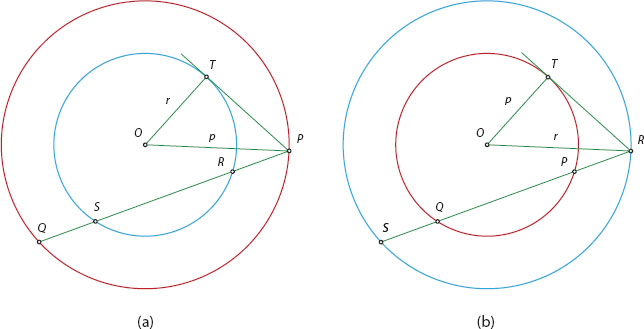
Let us denote the two circles by (O, p) and (O, r), where O is their common center and p = and r = are their radii (see figure 12.1, where (O, p) is marked in red and (O, r) in blue). We notice that the two circles can be interchanged by simply switching the roles of P and R and of S and Q. In figure 12.1(a), P is outside (O, r) and we have ; in (b), P is inside (O, r) and we have . But note that , because P and Q are symmetrically positioned with respect to O (as are R and S); consequently, we can rewrite the last equation as . But this is exactly the same equation as in case (a)! We can, therefore, combine theorems 35 and 36 into a single statement:

If through a point P a line is drawn that cuts a circle (O, r) at points R and S, the product is constant for all possible lines through P. If P is outside (O, r), this product is the square of the tangent from P to (O, r); if P is inside (O, r), it is the square of the tangent from R to (O, p).

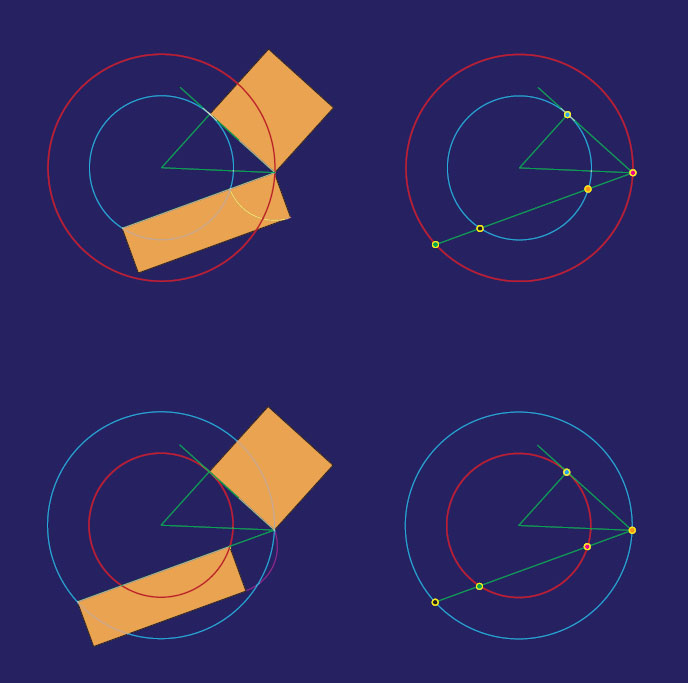
Plate 12 illustrates the complete symmetry between the two theorems. The top two figures illustrate theorem 36, the bottom two, theorem 35. The “given” and “implied” circles are marked in blue and red, respectively; the yellow rectangles and squares represent the product and the quantities (in the top figure) and (bottom figure). The two configurations are exactly the same, except that the given and implied circles reverse their roles.

The French mathematician Lazare Carnot (1753–1823) achieved this unification by regarding all line segments as directed quantities that can assume positive or negative values (for example, ). This, however, would not have sat well with Euclid, because the Greeks did not recognize negative quantities. Why, then, didn’t Euclid think of combining the two theorems the way we did here (that is, by regarding all line segments as nondirected quantities)? Surely he must have noticed the similarity between the two, but the idea of generalizing several particular cases into a broader, sweeping statement was foreign to the Greeks. To Euclid, each case represented a separate theorem, standing firmly on its own. Generalizations had to wait for future generations of mathematicians.¹

NOTE:

1. This chapter is based on an article by Maor published in The Mathematics Teacher (May 1979, pp. 363–367).