The Cycloid
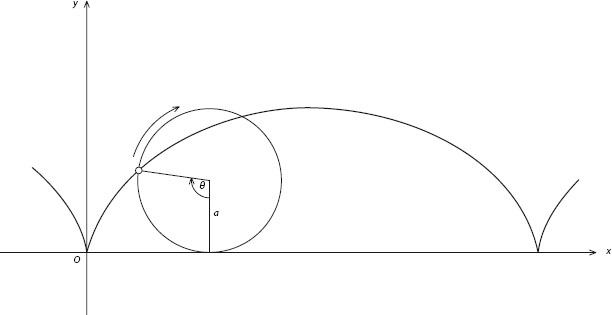
Rivaling the logarithmic spiral in elegance is the cycloid—the curve traced by a point on the rim of a circle that rolls along a straight line without slipping (figure 35.1). The cycloid is characterized by its arcs and cusps, each cusp marking the instant when the point on the wheel’s rim reaches its lowest position and stays momentarily ar rest.
The cycloid has a rich history. In 1673 Christiaan Huygens, whom we’ve just met in connection with the catenary, solved one of the outstanding problems that had intrigued seventeenth-century scientists: to find the curve down which a particle, moving only under the force of gravity, will take the same amount of time to reach a given final point, regardless of the initial position of the particle. This problem is known as the tautochrone (from the Greek words meaning “the same time”). To his surprise, Huygens found that the curve is an arc of an inverted cycloid. He tried to capitalize on his discovery by constructing a clock whose pendulum was constrained to swing between two adjacent arcs of a cycloid, so that the period of oscillations would be independent of the amplitude (in an ordinary pendulum this condition holds only approximately). Unfortunately, although the theory behind it was sound, the performance of Huygens’s clock fell short of his expectations.
Shortly thereafter the cycloid made history again. In 1696 Johann Bernoulli (1667–1748), the younger brother of Jakob (of logarithmic spiral fame), posed this problem: to find the curve along which a particle, again subject only to the force of gravity, will slide down in the least amount of time. You might think this should be the straight line connecting the initial and final positions of the particle, but this is not so: depending on the path’s curvature, the particle may accelerate faster at one point and slower at another, showing that the path of shortest distance between two points is not necessarily the path of shortest time.
Known as the brachistochrone (“shortest time”), this problem was attempted by some of the greatest minds of the seventeenth century. Among them was Galileo, who incorrectly thought the required path is an arc of a circle. In the end, five correct solutions were submitted in response to Johann Bernoulli’s challenge—by Newton, Leibniz, L’Hospital (famous for a rule in calculus named after him), and the two Bernoulli brothers, who worked on the problem independently and used different methods. To their surprise, the curve turned out to be an inverted cycloid—the same curve that solved the tautochrone problem. But instead of rejoicing in their success, the discovery embroiled the two brothers in a bitter priority dispute, resulting in a permanent rift between them.
The cycloid had some more surprises in store. Evangelista Torricelli (1608–1647), famous for his invention of the mercury barometer, is credited with finding the area under one arc of the cycloid: the area turned out to be 3πa2, where a is the radius of the generating circle. A few decades later Christopher Wren (1632–1723), London’s venerable architect who rebuilt the city after the Great Fire of 1666, found that the length of each arc is 8a; surprisingly, the constant π is not involved. This was one of the first successful rectifications of a curve—finding the arc length between two points on the curve. With the invention of calculus in the decade 1666–1676, problems like these could be solved routinely, but in the early seventeenth century they presented a challenging task.
Plate 35, Reflections on a Rolling Wheel, shows the path of a luminous point attached to a rolling wheel at three different distances from the center: at top, the point is outside the wheel’s rim (as on the flank of a railroad car wheel); at the middle, it is exactly on the rim; and at the bottom, inside of it. The top and bottom curves are called prolate and curtate cycloids, respectively, while the middle curve is the ordinary cycloid. You can see the curtate variant at night as the path traced by the reflector on a bicycle wheel as the cyclist moves forward.1
NOTE:
1. For a full history of the cycloid, see the article “The Helen of Geometry” by John Martin, The College Mathematics Journal (September 2009, pp. 17–27).