Conics
Imagine slicing a cone—for illustration’s sake think of it as an ice cream cone—with a swift stroke of a knife. If you slice it in a plane parallel to the cone’s base, you get a circular cross section. Tilt the angle slightly, and you get an ellipse. Tilt the angle even more, and the ellipse becomes narrower, until it no longer closes on itself: it becomes a parabola. This happens when the cut is parallel to the side of the cone. Increase the angle yet again, and you get two disconnected curves, the two branches of a hyperbola (provided you regard the cone as a double cone joined at its apex). Taken together, these curves—to which we may add a pair of straight lines when the cut is along the cone’s axis—comprise the five conic sections (figure 29.1).
The Greek mathematician Apollonius of Perga (ca. 262–190 BCE) wrote an extensive treatise on the conic sections. He gave them the names ellipse, parabola, and hyperbola, according to whether the cut is at an angle smaller than, equal to, or greater than the angle between the cone’s base and its side.
The conics are endowed with numerous properties, some shared by the entire family, while others are unique to each member. Let us begin with the parabola. On a sheet of paper draw a line d and choose a point F not on d. The parabola is the set (“locus”) of all points equidistant from d and F (figure 29.2). d is called the directrix, and F, the focus of the parabola. Like all conics, the parabola is a symmetric curve: its axis of symmetry passes through F and runs at a right angle to d. As Archimedes had discovered, rays of sunlight arriving at the parabola in a direction parallel to its axis are reflected toward a single point, the focus, as shown in plate 29.1 (indeed, “focus” in Latin means fireplace). This property finds its modern use in the ubiquitous satellite antenna dish—a concave surface with a parabolic cross section that, when aimed at a satellite in geostationary orbit, collects its signals at the focal point, where they are amplified and fed into your TV screen. It also works in reverse: if a source of light or a radio transmitter is placed at the focus, the emitted beam will be reflected in a direction parallel to the parabola’s axis, a feature brought to good use in the reflective surface of a car’s headlights.
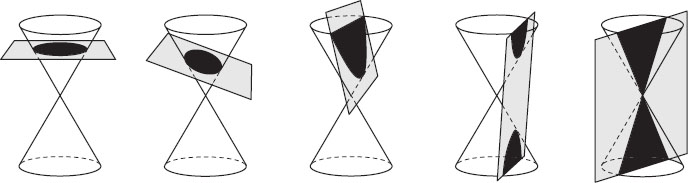
Figure 29.1
![]()
The ellipse is the locus of points, the sum of whose distances from two fixed points, the ellipse’s foci, is constant. A ray of light emanating from one focus is reflected by the ellipse toward the other focus. A striking example of this is the famous Whispering Gallery in the United States Capitol in Washington, DC, where visitors gathered at one focal point of the elliptically shaped hall can hear their guide, standing some distance away at the other focus, whisper some words seemingly to himself or herself. It never fails to impress the audience.
![]()
Like the ellipse, the hyperbola has two foci, but this time the difference of the distances from any point on the hyperbola to the foci is constant. The hyperbola consists of two disconnected branches, separated by two lines of demarcation that cross each other midway between the foci. These lines are the hyperbola’s asymptotes: they approach the hyperbola ever so close but never touch it—which is precisely what the word asymptote means: “don’t touch me.” The asymptotes are like signposts pointing the way to infinity.
A ray of light originating at one focus is reflected by the hyperbola in a direction away from the other focus. So the word focus in this case is really a misnomer: rather than concentrate at the focus, beams of light are scattered in every direction as they bounce off the hyperbola; “antifocus” would perhaps be a better name.
When you throw two stones into a pond, each will create a disturbance that propagates outward from the point of impact in concentric circles. The two systems of circular waves eventually cross each other and form a pattern of ripples, alternating between crests and troughs. Because this interference pattern depends on the phase difference between the two oncoming waves, the ripples invariably form a system of confocal ellipses and hyperbolas, all sharing the same two foci. In this system, no two ellipses ever cross one another, nor do two hyperbolas, but every ellipse crosses every hyperbola at right angles. The two families form an orthogonal system of curves, as we see in plate 29.2.
But the conic sections also play a role on a much grander scale. The German astronomer Johannes Kepler, whom we met already twice before, discovered that all planets move around the Sun in elliptical orbits. This discovery finally put to rest the old Greek belief that the planets move around the Earth in perfect circles or combinations of circles. A century later Isaac Newton would show that every celestial body—whether a planet, a comet, or a moon—moves around its parent body in an ellipse, a parabola, or a hyperbola. The conic sections thus became the cosmic sections.



