16

0.999 … = ?

When I ask beginning mathematics students, “is 0.999 … exactly equal to 1, or only approximately so?” their responses are usually split evenly, but occasionally the majority will vote for the second option. Well, let’s see:

Subtract the first equation from the second:

Surprising? … If this simple question can cause such disagreement today, how much more so in ancient times, when the idea of anything going on to infinity was so confusing that it was avoided entirely, shunned by the Greeks as horror infiniti, the horror of the infinite.

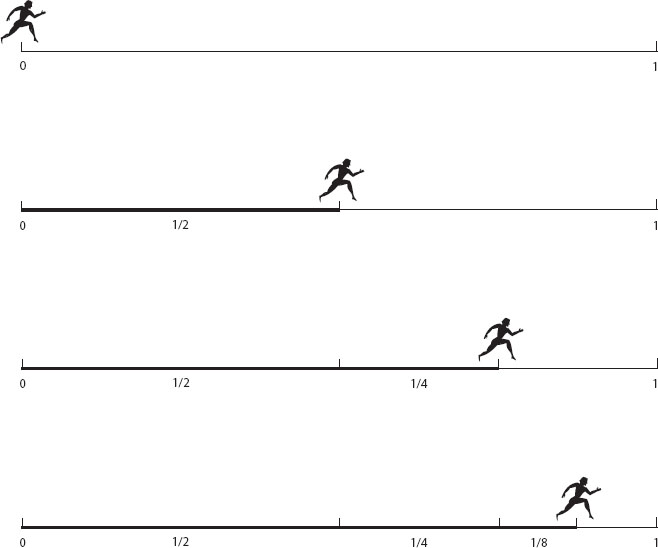
To make the point, the fourth-century BCE philosopher Zeno of Elea came up with four paradoxes—he called them “arguments”—meant to show that mathematicians were unable to deal with infinity. In one of these paradoxes Zeno purports to show that motion is impossible. Imagine an athlete about to run a 1-mile stretch. To do so, the runner would first have to cross the halfway point, then half of what’s still left (a quarter of the total distance), then half of that (an eighth), and so on ad infinitum (see figure 16.1). “Impossible!” said Zeno. No human can exhaust an infinite number of steps, so there will always be a tiny distance still left to be covered. The runner will be unable to reach the finish line; in fact, using the same argument, any kind of motion is impossible. Yet we do it all the time, giving no thought at all to the process.

At the heart of the runner’s paradox is the infinite series

Such a series, in which each term has a fixed ratio to its predecessor, is called a geometric series (for no particular connection to geometry). In the general case, a geometric series can be written as

where a is the initial term and r, the common ratio. If r is less than 1 in absolute value (that is, −1 < r < 1), the series will converge—it will reach a definite limit as the number of terms keeps growing. That is to say, by adding more and more terms, the sum will get ever closer to its limiting value, making the remaining difference as small as we please. In the case of the runner, we have

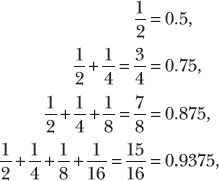
and so on. The sum seems to be getting ever closer to 1, the limiting value of the series.

Of course, adding the first few terms of our series does not prove that it converges to 1—or even that a limiting sum exists in the first place. Returning to the general case, it is not difficult to show that as long as −1 < r < 1, the limiting sum is a/(1 − r) (we give the proof in the appendix). For the runner’s paradox we have a = ½ and r = ½, so the sum is (½)/(1 − ½) = 1, and the runner will reach the finish line just fine.

Going back to the question we posed at the beginning of this chapter—is 0.999 … exactly equal to 1, or only approximately so?—we note that the repeating decimal 0.999 … is actually a geometric series, , whose initial term is a = >z/ and whose common ratio is r = ⅒. Since this common ratio satisfies the condition −1 < r < 1, the series will converge to the limit (>z/)/(1 − ⅒) = (>z/)/(>z/) = 1, settling the issue once and for all.

Zeno’s paradoxes caused a stir in the mathematical community that lasted well over two thousand years. Despite volumes of arguments, mostly philosophical or religious, no one was able to offer a convincing refutation of the paradoxes. And no wonder: to explain them, one must first accept the existence of infinity as a mathematical reality, a mental leap that even nineteenth-century mathematicians were not quite ready to take. It took the insight of a relatively unknown genius by the name Georg Cantor to take this crucial step, and in doing so he revolutionized our understanding of infinity. We will take a closer look at Cantor’s ideas in chapter 51. However, if you are still wondering how a string of nines can make up a 1, plate 16, 0.999 … = 1 will provide an answer—albeit a whimsical one.