Beyond Infinity
Can anything be larger than infinity? No, says common sense. But who is to say that common sense is always right—especially when it comes to the infinite, a world beyond our physical reach? “Infinity is a place where things happen that don’t,” an anonymous school pupil once said. Railroad tracks, though perfectly parallel, seem to meet far away on the horizon—at infinity; indeed, in projective geometry they do meet at infinity (see chapter 40). Yet when we try to reach that elusive point, it recedes from us just as fast as we approach it.
Again, when comparing two infinite sets, who is to tell which is the larger? There seem to be twice as many counting numbers as there are even numbers, and yet we can match every counting number with its double, showing that the two sets are just as large. And certainly there should be more points on a long line segment than on a short one, yet they both contain the same number of points—the same, in fact, as the entire number line (see figure 51.1). Strange, indeed, is the world of infinity.
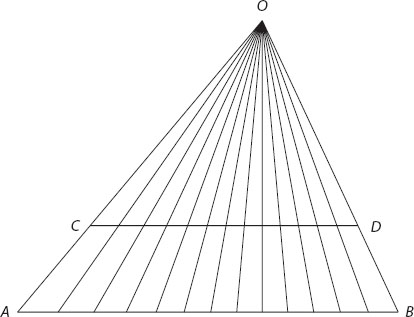
Figure 51.1
Enter Georg Cantor (1845–1918). Born in St. Petersburg, Russia, his family moved to Germany when he was 11. In 1869 he settled in the city of Halle, at whose university he would spend most of his productive years. Beginning in 1874, Cantor published a series of articles that at once put the concept of infinity on its head. To begin with, he insisted that an infinite set should be regarded in its entirety, as one whole. This ran smack against the accepted notion—going back to the Greeks—that infinity can be thought of only as a process, never as a finished product. For example, the act of counting the natural numbers 1, 2, 3, … can go on forever, yet at each stage only a finite number of them have been counted; the complete process can never be finished. Cantor thought otherwise: the natural numbers, he said, should be regarded as a single, complete object, symbolized by enclosing them in braces: {1, 2, 3, …}. In effect, Cantor declared that infinity, far from being the elusive goal of a never-ending process, is a mathematical reality.
But this was only the harbinger of things to come. Consider the set of rational numbers. We know that between any two fractions, no matter how close, you can always squeeze a third fraction. For example, between 1/1,001 and 1/1,000 you can fit the fraction 2/2,001 and, indeed, infinitely many more fractions. The rational numbers, then, are spread densely along the number line, and it would seem only natural to assume that there are many more of them than counting numbers—infinitely many more. But “natural” is a very poor guide when it comes to infinity. In a series of groundbreaking papers published in the decade 1874–1884, Cantor established three results that seem to defy common sense:
1. There are just as many positive rational numbers as counting numbers; that is to say, we can enlist all positive rationals in a row and count them one by one, without leaving a single one out, as depicted in plate 51. Cantor called any such set a countable, or denumerable, set. The even numbers, the odd numbers, the squares, the primes, and the rational numbers are all denumerable sets: their members can be put in a one-to-one correspondence with the counting numbers. Cantor denoted their infinity with the symbol ℵ0, the infinity of countable sets (ℵ, pronounced “aleph,” is the first letter of the Hebrew alphabet).
2. The real numbers, on the other hand, are uncountable—there are infinitely many more of them than there are counting numbers or rational numbers. They cannot be put in a 1:1 correspondence with any denumerable set; their infinity is of a higher rank than that of denumerable sets. Cantor assigned this kind of infinity the Gothic letter C, the infinity of the continuum. In the hierarchy of infinities, C > ℵ0.
3. There exist sets still more numerous than the reals and, therefore, of a higher degree of infinity than even C. Consider the set of all subsets of a given set—its power set. For example, starting with the two-element set {a, b}, we can create a new set that has all these elements as subsets: {{a}, {b}, {a, b}, { }} (note that we included the empty set, { }, among the subsets). This new set has 4 = 22 elements. We can now repeat the process with this new set, getting a power set of 16 = 24 elements. The number of subsets in this process grows very fast: the next power set will have 216 = 65,536 elements, and the one after that, 265,536 elements, approximately 1 followed by 19,728 zeros. The process can go on forever, generating ever-larger sets of enormous, yet still finite, size.
Cantor now imagined that we can do the same with infinite sets, generating a never-ending chain of power sets, each larger than its predecessor. Each of these sets stands one rung higher on the ladder of infinities. Cantor pointed out that these sets are purely a creation of the mind; they cannot be constructed in any “real” sense; they reside in the ethereal sphere of abstract mathematics. And yet their existence is as real as that of any other mathematical object, concrete or abstract.1
Cantor’s last years were not happy ones. Stung by the relentless opposition to his radical ideas and suffering from repeated spells of depression, he spent his final years in a mental institution, where he died in 1918. Yet his ideas slowly gained acceptance. In a way, he accomplished the vision of William Blake’s famous verse in Auguries of Innocence:
To see the world in a grain of sand,
And heaven in a wild flower.
Hold infinity in the palm of your hand,
And eternity in an hour
NOTE:
1. For a more complete account of Cantor’s theory, see Maor, To Infinity and Beyond, chapters 9 and 10 (Princeton, NJ: Princeton University Press, 1991).

