31

The Harmonic Series

In the last chapter we saw that the series 1 − ½ + ⅓ − ¼ + ··· converges to ln 2.

It is tempting to ask what will happen if we take the terms of this series in absolute value, that is, all positive. We then get the harmonic series, the sum of the reciprocals of the positive integers:

The name “harmonic” comes from the fact that a vibrating string produces not only one note but infinitely many higher notes, whose frequencies are 1, 2, 3, 4, 5, … times the fundamental, or lowest, frequency. It is one more example of the influence that music, and musical terminology, has had on mathematics.

Since the Middle Ages it was known that the harmonic series diverges—its sum grows without bound as we add more and more terms, despite the fact that the terms themselves get smaller and smaller. But you would never guess this from watching the sum grow, because the rate of divergence is agonizingly slow. Some numbers will make this clear: the sum of the first thousand terms of the series is 7.485, rounded to the nearest thousandth; the sum of the first million terms is 14.357; the first billion terms, about 21; the first trillion terms, about 28. But to make the sum exceed, say, 100, we would have to add up a staggering 10⁴³ terms (that’s 1 followed by 43 zeros). To get an idea of just how large this number is, suppose we were to write down the series, term by term, on a long paper ribbon until its sum surpasses 100, allocating 1 cm for each term (this is actually an underestimate, since the terms will require more and more digits as we go along). The ribbon will then be 10⁴³ cm long, which is about 10²⁵ light-years. But the size of the observable universe is at present estimated at only 10¹¹ light-years, so our ribbon would soon be running out of space to do the job! Yet if we could sum up the entire series—all its infinitely many terms—the sum would grow to infinity.

The divergence of the harmonic series was first proved by Nicole Oresme (ca. 1320–1382), a French theologian, economist, and mathematician. His proof is based on comparing the terms of the series with a second series in which the third and fourth terms are ¼ + ¼ instead of ⅓ + ¼, the fifth, sixth, seventh, and eighth terms are ⅛ + ⅛ + ⅛ + ⅛ instead of , and so on. Since , etc., we have

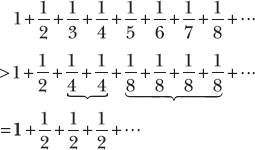
Each group of terms after the first in this second series is equal to ½, so the series grows to infinity. And since the original series is greater than 1 + ½ + ½ + ½ + ½ + ···, it too grows to infinity—it diverges.

The harmonic series gives rise to many surprises. For example, if we remove from it all the terms with composite denominators—leaving only prime-number denominators—the series will still diverge! This is rather remarkable, because the primes thin out as we go to higher numbers—they become ever more rare. And yet the sum of their reciprocals still diverges. On the other hand, the sum of the reciprocals of all twin primes (see page 45) is known to converge—although it is still an open question how many twin primes are there. So, until the issue is settled, we cannot say with unfailing certainty that this is an infinite series.

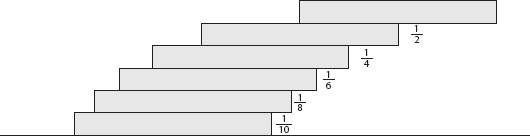
But perhaps the most amazing aspect of the harmonic series comes not from mathematics but from physics. Imagine stacking n identical domino tiles one on top of the other, but with each tile offset with respect to the one below it according to sequence (taking the length of each tile to be 1; see figure 31.1). The stack of dominoes will gradually curve and create an increasing overhang, and we would expect that its center of gravity will eventually extend beyond the bottom tile and cause the stack to collapse. Surprisingly, this does not happen: against all odds, the stack will survive intact, although just barely so (see plate 31). The overhang from stacking n dominos in this manner turns out to be . And since this finite harmonic series diverges as n → ∞, we could add on more and more tiles (starting at the bottom) and make the overhang as large as we please while the stack will maintain its equilibrium—though I wouldn’t recommend standing under it on a rainy day!¹

NOTE:

1. See John Bryant and Chris Sangwin, How Round is Your Circle: Where Engineering and Mathematics Meet (Princeton, NJ: Princeton University Press, 2008), pp. 255–59.