45

Symmetry II

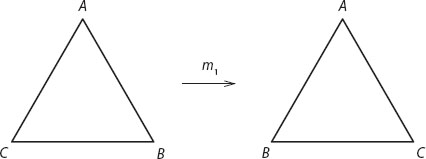
As we just saw, an equilateral triangle is endowed with six symmetry elements—three 120° rotations and three mirror reflections. Let the triangle be ABC, with vertex A at the top, followed clockwise by vertices B and C. Let us denote the six symmetry operations by letters: r₁, r₂, r₃ for the 120°, 240°, and 360° clockwise rotations and m₁, m₂, m₃ for the reflections in the altitudes through the top, lower-right, and lower-left vertices (henceforth we’ll refer to these vertices as nos. 1, 2, and 3 rather than A, B, and C, because they keep changing their position as we rotate and reflect the triangle; thus the position-1 vertex is always at the top, 2 is at lower right, and 3 is at lower left, regardless of the positions of A, B, and C).

Now a 120° rotation changes triangle ABC to CAB, which is just a cyclic permutation of the letters A, B and C, so that C now occupies the 1-position, A occupies the 2-position, and B the 3-position (see figure 45.1). In a similar way, a 240° rotation transforms ABC into BCA, and a 360° rotation changes ABC into … ABC—it brings the triangle back to its starting orientation. This, of course, should come as no surprise: a 360° rotation is the same as “doing nothing”—it leaves everything unchanged. To summarize,

Turning now to the reflections, we can summarize them as follows:

Note that in each reflection one letter stays put, while the other two switch positions—exactly what a mirror reflection does (figure 45.2).

We are now ready to produce our trump card: we can follow any of the six symmetry operations with a second symmetry operation; for example, a 120° rotation followed by a reflection in the 1-position amounts to

But CBA can be obtained directly from ABC by a reflection in the 2-position (in our case, vertex B; see figure 45.3). We call this combined application of two symmetry operations a product and denote it with a dot. And just as a product of two numbers gives us a third number, a product of two symmetry operations results in a third symmetry operation. In the example just given, this amounts to writing r₁ · m₁ = m₂.

We have, in effect, created a kind of algebra of symmetry operations, similar in some ways to the ordinary algebra of numbers and variables we learn in school, but with one crucial difference: unlike numbers, the product of two symmetry operations is generally noncommutative—the order in which we perform the operations does matter. To see this, let us again find the product of r₁ and m₁, but this time in reverse order:

That is to say, m₁ · r₁ = m₃, whereas r₁ · m₁ = m₂. Thus, r₁ · m₁ ≠ m₁ · r₁.

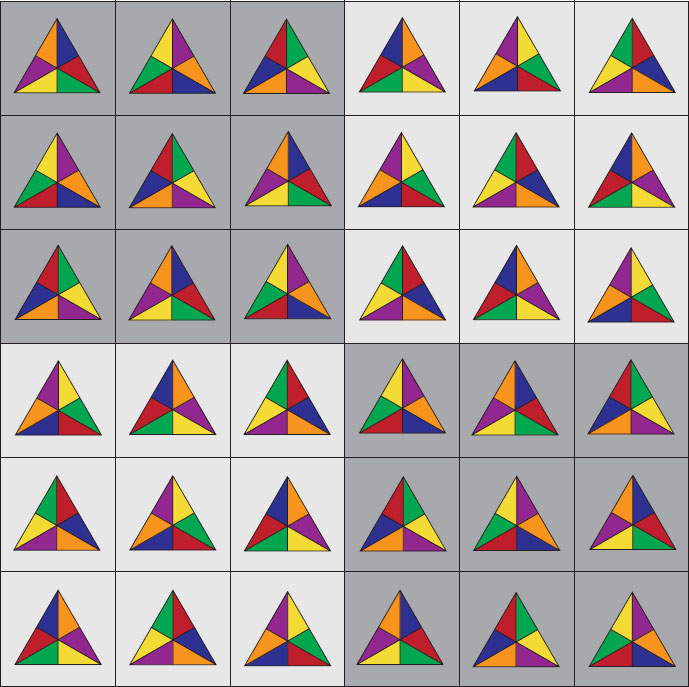
If you are willing to spend a few more minutes on this exercise (it may remind you of your daily Sudoku), you can create a complete “multiplication table” of the six symmetry operations of the equilateral triangle. Here it is:

Plate 45 shows all 36 entries of this table in a rainbow display of color. Note that the upper-left and lower-right quadrants (on gray background) consist of rotations alone, while the remaining two quadrants are pure reflections. We can summarize this in a miniature table:

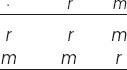
Here, r and m stand for rotations and reflections of any kind. As this table shows, a succession of two rotations or two reflections always results in a rotation, whereas a rotation and a reflection result in a reflection. You can convince yourself of this when looking in the mirror: what you see is not yourself but a mirror image of yourself; if you stretch out your right hand, your image will respond with its left hand! To see a true image of yourself, you have to look at the intersection of two mirrors at right angles to each other; you will see yourself as someone else sees you.

Returning to the triangle’s multiplication table, four features about this table are worth noting:

1.  The table is “closed” in the sense that no matter which two symmetry operations you choose to multiply, their product will again be one of the six symmetry operations: you can never go outside this set.

2.  Among the members of our set there is one element that has the effect of “doing nothing.” This, of course, reminds us of the number 1 in ordinary multiplication: 1 · a = a for any number a. And indeed, this particular element, called the unit or identity element, is r₃, the 360° rotation, since it leaves the triangle in its original position.

3.  Just as with numbers, any multiplication in our set can be undone; that is, every element has an inverse, whose product with the original element results in the identity element. For example, the inverse of r₁ is r₂, because r₁ · r₂ = r₃. The inverse of any reflection is the same reflection again, since the mirror image of a mirror image is the original image: a reflection is its own inverse.

4.  If you multiply together three elements, the order of grouping does not matter; symbolically, a · (b · c) = (a · b) · c. This is the associative law, with which we are familiar from ordinary arithmetic. You can convince yourself of the validity of this law by trying a few examples (or, if you have the patience, all 432 = 2 · 6³ possible combinations); for example, r₁ · (m₃ · r₂) = r₁ · m₁ = m₂, while (r₁ · m₃) · r₂ = m₁ · r₂ = m₂: you get the same answer.

Any collection of objects—whatever their nature—that fulfills these four requirements is called a group. It was this concept that Abel and Galois independently introduced in their quest for a formula for solving the general quintic (Galois suggested the name). For more than a hundred years the group concept was regarded as a purely abstract creation, devoid of any practical applications. But with the rise of modern physics in the twentieth century, group theory suddenly assumed central stage in nearly every branch of science, from crystallography and quantum mechanics to relativity and particle physics.

One of the great accomplishments of modern mathematics was achieved between 1995 and 2004 with the successful classification of all finite simple groups—groups with a finite number of elements from which all other groups can be created, in much the same way as any integer can be created by multiplying together its prime factors. This achievement, the result of a collaboration of more than 100 mathematicians, has been compared in its importance to the discovery half a century earlier of the DNA double helix and the genetic code.