PROOFS OF SELECTED THEOREMS MENTIONED IN THIS BOOK
QUADRILATERALS (PAGE 6)
We refer to figure A.1. Let □ABCD denote the area of quadrilateral ABCD, ΔABD, the area of triangle ABD, etc. Because triangle APS has half the base length and half the height of triangle ABD, we have ΔAPS = ¼ΔABD. Similarly, ΔCQR = ¼ΔCBD. Thus,
![]()
By the same argument,
![]()
Therefore,

The proof still holds when the quadrilateral has the shape of a dart (see figure A.2), except that some of the internal areas must be subtracted rather than added. We leave the proof of this case to the reader.
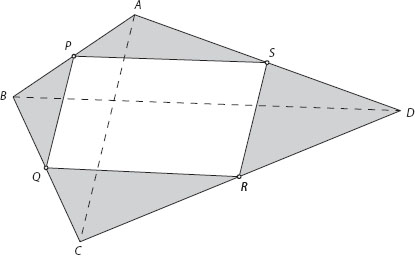
Figure A.1
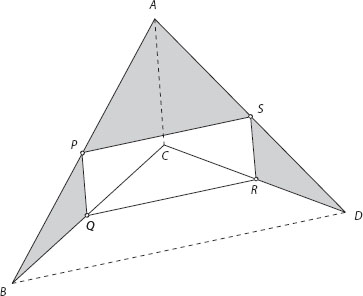
Figure A.2
Let u and v be any positive integers, with u > v. Set a = u2 − v2, b = 2uv, and c = u2 + v2. Then

showing that (a, b, c) is a Pythagorean triple. For example, if u = 5 and v = 3, we get a = 52 − 32 = 25 − 9 = 16, b = 2 × 5 × 3 = 30, and c = 52 + 32 = 25 + 9 = 34, giving us the triple (16, 30, 34).
In this example we got a nonprimitive triple, being merely a magnification of the triple (8,15,17) by a factor of 2. To get primitive triples, two restrictions must be imposed on u and v: they must be relatively prime (having no common factors other than 1), and they must be of opposite parities—one even and the other odd. For example, choosing u = 5 and v = 4 gives us the primitive triple (9, 40, 41).
Since the choice of u and v is otherwise arbitrary, we see that there are infinitely many primitive Pythagorean triples. The converse is also true: every primitive Pythagorean triple corresponds to a pair of values (u, v) subject to the restrictions mentioned previously. For the details, see Maor, The Pythagorean Theorem: A 4,000-Year History, pp. 221–22.
A PROOF THAT ![]() IS IRRATIONAL (PAGE 23)
IS IRRATIONAL (PAGE 23)
The proof is by the indirect method: we assume that ![]() is rational and then show that this leads to a contradiction.
is rational and then show that this leads to a contradiction.
Suppose ![]() is rational, that is,
is rational, that is, ![]() = m/n, where m and n are two positive integers with no common factor other than 1. Rewriting this equation as m =
= m/n, where m and n are two positive integers with no common factor other than 1. Rewriting this equation as m = ![]() n and squaring both sides, we get m2 = 2n2, which means that m2—and, therefore, m—is an even integer (since the square of an odd integer is always odd). So m = 2r for some integer r. Putting this back into the equation m2 = 2n2, we get 4r2 = 2n2, or n2 = 2r2. But this means that n2—and, therefore, n—is also even, so n = 2s for some integer s. Thus, m and n have a common factor 2, in contradiction to our assumption that the fraction m/n is in lowest terms. We conclude that
n and squaring both sides, we get m2 = 2n2, which means that m2—and, therefore, m—is an even integer (since the square of an odd integer is always odd). So m = 2r for some integer r. Putting this back into the equation m2 = 2n2, we get 4r2 = 2n2, or n2 = 2r2. But this means that n2—and, therefore, n—is also even, so n = 2s for some integer s. Thus, m and n have a common factor 2, in contradiction to our assumption that the fraction m/n is in lowest terms. We conclude that ![]() is not rational—QED.
is not rational—QED.
EUCLID’S PROOF OF THE INFINITUDE OF THE PRIMES (PAGE 44)
We again follow an indirect proof (a proof by contradiction). Assume there is only a finite number of primes, p1, p2, p3, …, pn Now consider the number N = p1 · p2 · p3 · … · pn + 1. This number is obviously greater than any of the pi, yet it is not divisible by any of them, because any such division will leave a remainder 1. Therefore, N must either be a new prime, not included in the original list, or else it is composite, in which case at least one of its prime factors must be a new prime not included in the original list. In either case we have a contradiction, for we assumed that the set p1, p2, p3, …, pn included all the primes—QED.
To illustrate, suppose there are only three primes, 2, 3, and 5. Then N = 2 · 3 · 5 + 1 = 31, a new prime. On the other hand, if we started with 3, 5, and 7, we would get N = 3 · 5 · 7 + 1 = 106 = 2 · 53, producing two new primes that were not in the original set. We can then add these primes to our list and start the process again, generating ever more primes (although not all of them, and not in sequential order), like a runaway nuclear chain reaction, but fortunately with less-dire consequences.
THE SUM OF A GEOMETRIC PROGRESSION (PAGE 51)
Consider the finite geometric progression a, ar, ar2, …, arn−1 of n terms. Let its sum be S:
![]()
Multiply this equation by the common ratio r:
![]()
Subtract the second equation from the first: all terms cancel out except the first and last:
![]()
or S(1 − r) = a(1 − rn), from which we get
![]()
provided, of course that r ≠ 1. Now, if r is less than 1 in absolute value (that is, −1 < r < 1), the term rn gets smaller and smaller as n increases; that is, rn → 0 as n → ∞. Thus, the sum of the infinite progression is
![]()
THE SUM OF THE FIRST n FIBONACCI NUMBERS (PAGE 64)
Let F1 = F2 = 1, Fi = Fi−2 + Fi−1 for i = 3, 4, …. Note that
![]()
Adding up these expressions, we get, on the left side, F1 + F2 + F3 + ··· + Fn, while on the right side all terms except −F2 and Fn+2 cancel out. Remembering that F2 = 1, we thus get
![]()
A slightly different formula holds for the sum of the squares of the first n Fibonacci numbers:
![]()
as can be proved by mathematical induction.
Many more Fibonacci-related formulas can be found in Alfred S. Posamentier and Ingmar L. Lehmann, The (Fabulous) Fibonacci Numbers (Amherst, NY: Prometheus Books, 2007).
CONSTRUCTION OF A REGULAR PENTAGON (PAGE 70)
We first show that the 72-72-36-degree triangle formed by any side of the pentagon and the vertex opposite it has a side-to-base ratio equal to the golden ratio ![]() .
.
Let the triangle be ABC, with the 36° angle at C (figure A.3). Bisect angle A and extend the bisector until it meets side BC at D. This produces two isosceles triangles—the 72-72-36-degree triangle BDA and the 36-36-108-degree triangle ACD. Of these, the former is similar to triangle ABC, so we have
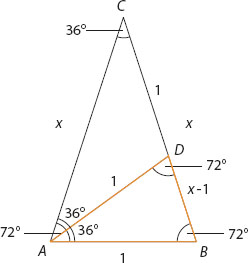
Figure A.3
![]()
(all line segments are nondirectional, so that ![]() =
= ![]() ). Setting
). Setting ![]() = 1 and
= 1 and ![]() = x, we have
= x, we have ![]() . We thus get
. We thus get
![]()
which leads to the quadratic equation x2 − x − 1 = 0. Solving it and taking only the positive solution (because x stands for length, which cannot be negative), we get
![]()
which is exactly the golden ratio φ.
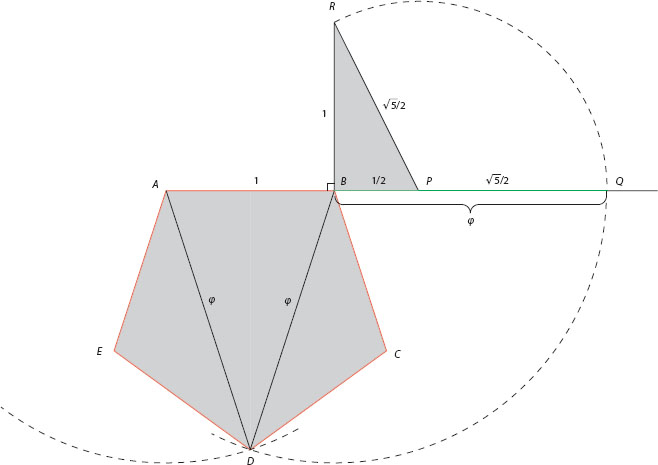
Figure A.4
To construct a pentagon with unit side, we first need to construct a segment equal in length to the golden ratio. Referring to figure A.4, draw a unit line segment ![]() = 1, extend it to the right by segment
= 1, extend it to the right by segment ![]() , and at B erect a perpendicular
, and at B erect a perpendicular ![]() . We have
. We have ![]() . Place your compass at P and swing an arc of radius
. Place your compass at P and swing an arc of radius ![]() , meeting the extended segment
, meeting the extended segment ![]() at Q. We have
at Q. We have
![]()
We are now ready to construct our pentagon. Place your compass at B and swing an arc of radius ![]() ; then do the same with your compass at A (only the first of these arcs is shown in full in figure A.4). The two arcs intersect at D. Next, from each of the points A and D swing an arc of radius
; then do the same with your compass at A (only the first of these arcs is shown in full in figure A.4). The two arcs intersect at D. Next, from each of the points A and D swing an arc of radius ![]() ; the two arcs intersect at E (see following note). Do the same from points B and D, producing point C. Connect points A, B, C, D and E, and your pentagon is complete.
; the two arcs intersect at E (see following note). Do the same from points B and D, producing point C. Connect points A, B, C, D and E, and your pentagon is complete.
Note: for the arcs to intersect, each radius must be greater than half the segment. Indeed, ![]() , ensuring that the arcs meet.
, ensuring that the arcs meet.
For further discussion and alternative ways to construct a pentagon, see Hartshorne, Geometry: Euclid and Beyond, chapter. 4, and Heilbron, Geometry Civilized, pp. 221–228.
CEVA’S THEOREM (PAGE 105)
Let the triangle be ABC (figure A.5), and let A′, B′, and C′ be any points on the sides opposite to A, B, and C such that AA′, BB′, and CC′ pass through one point G. Ceva thought of this point as the center of gravity of weights WA, WB, and WC attached to the respective vertices. Let us find the center of gravity of any two of these weights, say WB and WC; call this point A′. By Archimedes’s law of the lever (the “see-saw rule”), we have
![]()
from which we get
![]()
In a similar manner we get for the other two pairs of points,
![]()

Figure A.5
Multiplying the three ratios, we get
![]()
Note that in forming this triple product, we went in a counterclockwise direction around the triangle, from B to A′ to C, then to B′, and so on. Since the center of gravity G of the entire triangle must lie on each of the lines AA′, BB′, and CC′, it must lie on their intersection, so the three lines are concurrent. Interestingly, the actual weights disappeared from the final result—they just served as a tool and canceled out at the end.
This, of course, is a physically motivated proof with which a pure mathematician might disagree. But let us remember that Archimedes, the quintessential pure mathematician, often used subtle physical reasoning in his proofs, yet he always supplemented them with a rigorous mathematical argument. For a strictly geometric proof, see Eves, A Survey of Geometry, pp. 247–48.
SOME PROPERTIES OF INVERSION (PAGE 128)
Let the circle of inversion be c, with center at O and radius 1 (figure A.6). We first show that inversion transforms a straight line not through O into a circle through O. Let the line be l. Choose two points on l, the point P closest to O and any other point Q, and let their images under inversion be P′ and Q′, respectively. By the definition of inversion we have ![]() , from which we get
, from which we get
![]()
This means that triangles OPQ and OQ′P′ are similar. Since P is the point on l closest to O, line OP is perpendicular to l, so ΔOPQ is a right triangle with its right angle at P. Therefore, triangle OQ′P′ is also a right triangle with its right angle at Q′, and this is true regardless of the position of Q on l. Thus, by the converse of Thales’s theorem (see chapter 1, note 1), as Q moves along l, its image Q′ describes an arc of a circle k with diameter OP′.
The converse of this property is also true: inversion carries a circle through O onto a line not through O. This can be seen by simply reading figure A.6 “backward,” from circle k to line l. This is a result of the fact that inversion is completely symmetric: if P′ is the image of P, then P is the image of P′, as can be seen from the equivalence of the defining equations ![]()
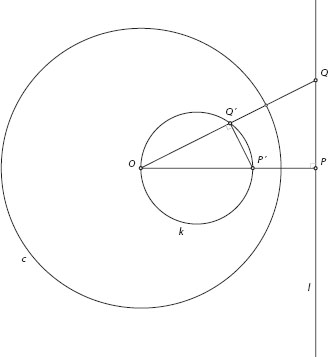
Figure A.6
It can also be shown that inversion carries a circle not through O to another circle not through O. For the details, see Courant and Robins, What is Mathematics, pp. 142–144.
