Perfect Numbers and Triangular Numbers
The Pythagoreans—the school founded by Pythagoras in the fifth century BCE—had a special relationship with numbers (the term here meaning positive integers). In their mind, numbers were not just a measure of quantity but symbols possessing mythical significance. The number 1 was not considered a number at all, but rather the generator of all numbers, since every number can be obtained from it by repeated addition. Two symbolized the female character, 3 the male character, and 5 their union. Five was also the number of Platonic solids—convex polyhedra whose faces are all identical regular polygons (although the proof that there are exactly 5 of them came only later). These 5 solids are the tetrahedron, having 4 equilateral triangles as faces, the cube (6 square faces), the octahedron (2 square pyramids joined at their bases and comprising 8 equilateral triangles), the dodecahedron (12 regular pentagons), and the icosahedron (20 equilateral triangles); they are shown in figure 4.1. No wonder, then, that the number 5 acquired something of a sacred status with the Greeks.
Even more revered than five was the number 6, the first perfect number, being the sum of its proper divisors, 1 + 2 + 3.1 The next perfect number is 28 (= 1 + 2 + 4 + 7 + 14), followed by 496 and 8,128. These were the only perfect numbers known in antiquity. As of this writing, 48 perfect numbers are known; the largest, discovered in 2013, is 257,885,160 · (257,885,161 − 1), an enormous number of nearly 35 million digits. The question of how many perfect numbers exist—or even whether their number is finite or infinite—is still unanswered.
Six is also a triangular number, so called because these numbers form a triangular pattern when arranged in rows of 1, 2, 3, … dots. The first four triangular number are 1, 1 + 2 = 3, 1 + 2 + 3 = 6, and 1 + 2 + 3 + 4 = 10, followed by 15, 21, and so on. The Pythagoreans discovered several relations between these sequences of integers. For example, the nth triangular number is always equal to n(n + 1)/2 (you can check this for a few cases: 1 + 2 + 3 = 6 = (3 × 4)/2, 1 + 2 + 3 + 4 = 10 = (4 × 5)/2, etc.). So this gives us a convenient way—a formula—for finding the sum of the first n integers without actually adding them up:

Figure 4.1
![]()
When we add instead the first n odd integers, a surprise is awaiting us: the result is always a perfect square: 1 = 12, 1 + 3 = 4 = 22, 1 + 3 + 5 = 9 = 32, and, in general,
![]()
Still another relation comes from adding two consecutive triangular numbers; again you get a perfect square: 1 + 3 = 4 = 22, 6 + 10 = 16 = 42, 10 + 15 = 25 = 52, and so on. This is true because
![]()
Perhaps most surprising of all is the fact that every perfect number is also a triangular number. Thus 6, 28, 496, and 8,128 are the 3rd, 7th, 31st, and 127th triangular numbers, respectively, and 257,885,160 · (257,885,161 − 1) is the (257,885,161 − 1)th triangular number.2 Euclid, in his Elements (see page 3), proved that if 2n − 1 is prime, then 2n−1 · (2n − 1) is perfect.3 More than two thousand years later, Leonhard Euler proved the converse: every even perfect number is of the form 2n−1 · (2n − 1) for some prime value of n. All 48 perfect numbers known today are even; whether any odd perfect numbers exist is unknown and remains one of the great mysteries of mathematics. Should such a number be found, it would be an oddity indeed!
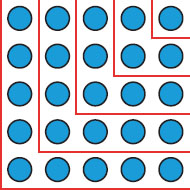
Figure 4.3
The Pythagoreans established these relations, and many others, by representing numbers as dots arranged in various geometric patterns. For example, figure 4.2 shows two triangular arrays, each representing the sum 1 + 2 + 3 + 4. Taken together, they form a rectangle of 4 × 5 = 20 dots. Therefore, the required sum is half of that, or 10. Repeating this for other numbers of dots, it would have been easy for the Pythagoreans to arrive at the formula 1 + 2 + 3 + ··· + n = n(n + 1)/2. Similarly, figure 4.3 illustrates how they would have established the formula 1 + 3 + 5 + 7 + ··· + (2n − 1) = n2, while figure 4.4 demonstrates that the sum of two consecutive triangular numbers is always a perfect square. The Pythagoreans viewed these relations as purely geometric; today, of course, we prefer to prove them algebraically. Yet, in discovering them, the Greeks sowed the seeds that many centuries later would evolve into modern number theory, the branch of mathematics concerned with the positive integers.

Figure 4.4
Plate 4, Figurative Numbers, is a playful meditation on ways of arranging 49 dots in different patterns of color and shape. Some of these arrangements hint at the number relations we mentioned previously, while others are artistic expressions of what a keen eye can discover in an assembly of dots. Note, in particular, the second panel in the top row: it illustrates the fact that the sum of eight identical triangular numbers, plus 1, is always a perfect square.4
NOTES:
1. The proper divisors of a number are all positive integers that divide it evenly, including 1 but excluding the number itself.
2. To see this, write 257,885,160 · (257,885,161 − 1) as [257,885,161 · (257,885,161 − 1)]/2 and let n = 257,885,161 − 1. Then the expression has the form (n + 1)n/2, a triangular number.
3. For more on primes of the form 2n − 1, see chapter 14.
4. This is because 8 · (n + 1)n/2 + 1 = 4n2 + 4n + 1 = (2n + 1)2.


