11

Two Theorems from Euclid

Theorem 35 of the third book of the Elements says, If in a circle two straight lines cut one another, the rectangle contained by the segments of the one is equal to the rectangle contained by the segments of the other.

To make sense of this enigmatic statement, we must understand that the Greeks always used geometric language to describe operations that nowadays would be stated in algebraic terms. Thus, “the rectangle contained by” is code for “the product of” [the sides of the rectangle]—in other words, the area of the rectangle. Translated into modern language, the theorem says: if through a point P inside a circle we draw a line that cuts the circle at points A and B, the product is constant; it has the same value for all lines through P (see figure 11.1, where ).

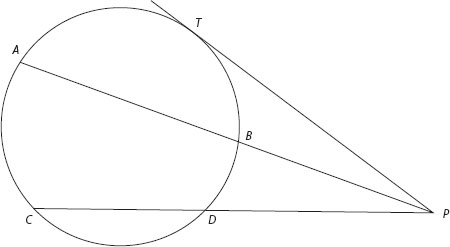
This is followed by theorem 36: If a point be taken outside a circle and from it there fall on the circle two straight lines, and if one of them cut the circle and the other touch it, the rectangle contained by the whole of the straight line which cuts the circle and the straight line intercepted on it outside between the point and the convex circumference will be equal to the square on the tangent.

Again, behind this seemingly convoluted language is the statement: if from a point P outside a circle we draw a line that cuts the circle at points A and B, the product is constant for all possible lines through P and is equal to the square of the length of the tangent line from P to the circle (figure 11.2, where ). Note that the phrase the square on the tangent actually means the area of a square whose side equals the length of the tangent line.

The proof of theorem 35 is quite simple. In figure 11.3, P is a point inside the circle, and and are two chords passing through P. We have ∠APC = ∠BPD and ∠ACD = ∠DBA, the latter equality because angles ∠ACD and ∠DBA subtend the same arc, , on the circumference (Euclid III, 21). Thus, triangles PAC and PDB are similar, having two pairs (and, therefore, three) of equal angles. Consequently, , which means that the product is constant for all possible lines through P.

The proof of theorem 36 follows similar lines, and we leave it to the reader to work out the details. The additional statement, that the product is equal to the square of the tangent line from P to the circle, can be thought of as a limiting case when point A approaches point B, ultimately to coincide with the point of tangency T. We then have . We should note, however, that the Greeks would not have accepted such a limiting argument into their reasoning because it subtly involves the notions of motion and continuity, two concepts that Euclid regarded as physical in nature and thus foreign to pure mathematical thinking.

Our illustration (plate 11) shows four identical circles, each with a pair of chords intercepting at P. The two upper circles (with P outside each circle) illustrate theorem 36 and the two lower circles (P inside), theorem 35. In each case, × is represented by a rectangle of sides and (shown in orange), and since this product is constant for all possible chords through P, the two rectangles on either side of each circle are equal in area.