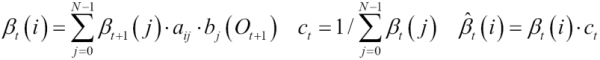One of the challenges of describing the hidden Markov model is the mathematical notation that sometimes differs from author to author. From now on, we will use the following notation:

For convenience, let's simplify the notation of the sequence of observations and states using the following condensed form: p(O_0:T, q_t| λ) = p(O₀, O₁, … O_T, q_t| λ). It is quite common to visualize a hidden Markov model with a lattice of states and observations similar to our description of the boxes and balls examples, as shown here:

The formal HMM-directed graph

The state S_i is observed as O_k at time t, before being transitioned to the state S_j observed as O_m at the time t+1. The first step in the creation of our HMM is the definition of the class that implements the lambda model λ = (π, A, B) [7:4].

The three canonical forms of the hidden Markov model rely heavily on manipulation and operations on matrices and vectors. For convenience, let's define an HMMConfig class that contains the dimensions used in the HMM:

class HMMConfig(val _T: Int, val _N: Int, val _M: Int) extends Config

The input parameters for the class are:

The HMMConfig companion object defines the operations on ranges of index of matrix rows and columns. The foreach, foldLeft, and maxBy methods are regularly used in each of the three canonical forms:

object HMMConfig {
   def foreach(i: Int, f: Int => Unit): Unit = Range(0, i).foreach(f)
   def foldLeft(i: Int, f: (Double, Int) => Double, zero:Double) = Range(0, i).foldLeft(zero)(f)
   def maxBy(i: Int, f: Int => Double): Int = Range(0,i).maxBy(f)
   …
}

As mentioned earlier, the lambda model is defined as a tuple of the transition probability matrix A, emission probability matrix B, and the initial probability π. It is easily implemented as a case class, HMMLambda, using the Matrix class defined in the Matrix class section in Appendix A, Basic Concepts. The simplest constructor for the HMMLambda class is invoked in the case where the state-transition probability matrix, the emission probability matrix, and the initial states are known, as shown here:

class HMMLambda(val A: Matrix[Double], val B: Matrix[Double], var pi: DblVector, val numObs: Int) {
  def getT: Int = numObs
  def getN: Int = A.nRows
  def getM: Int = B.nCols
  val d1 = numObs -1
…
}

The implementation reflects the mathematical notation, with pi being the initial state probability, A the state transition matrix, and B the emission matrix. The numObs value is the number of observations in the sequence. The getT, getN, and getM methods are used to keep the implementation consistent with the initial configuration, HMMConfig. The section related to the training of HMM introduces a different constructor for HMMLambda using the configuration as a parameter.

The initial probabilities are unknown, and therefore, initialized with a random generator of values [0, 1].

The two other components of the HMM are the sequence of observations and the sequence of hidden states.

The canonical forms of the HMM are implemented through dynamic programming techniques. These techniques rely on variables that define the state of the execution of the HMM for any of the canonical forms:

Each of the parameters is described in the section related to each canonical form. Let's create a class HMMState that encapsulates the variables used in the implementation of the three canonical cases.

For convenience, all the parameters related to the three canonical cases and listed in the previous notation section are encapsulated into a single outer class, HMMState:

class HMMState(lambda: HMMLambda, maxIters:Int) extends Config {
  val delta = Matrix[Double]( lambda.getT, lambda.get N)  // δt(i)

  object QStar { … } //q*
  object DiGamma { … } // γt(i, j)
  object Gamma { … }  // γt(i)
}

Once again, we use the same notation as for the configuration of the HMM; lambda.getT, being the number of observations, and lambda.getN, the number of hidden states. The HMM state parameters have self-descriptive names that strictly follow the notation introduced earlier. The model, the HMM state, and the sequence of observations are all the elements needed to implement the three canonical cases.

The Gamma and DiGamma singletons are used and described in the evaluation canonical form. The DiGamma singleton is described as part of the Viterbi algorithm to extract the sequence of states with the highest probability given a model and a set of observations.

The execution of any of the three canonical forms relies on dynamic programming techniques (refer to the Overview of dynamic programming section in Appendix A, Basic Concepts) [7:5]. The simplest of the dynamic programming techniques is a single traversal of the observations/state chain.

Therefore, it makes sense to define a base class, HMMModel, that has all the algorithms that manipulate the model, lambda, and the observed states, obs:

abstract class HMMModel(lambda: HMMLambda, obs: Array[Int])

The list of dynamic-programming-related algorithms used in any of the three canonical forms is visualized through the class hierarchy of our implementation of the HMM:

Scala classes' hierarchy for HMM (UML class diagram)

Each class is described as needed in the description of the three canonical forms of HMM. It is time to dive into the implementation details of each of the canonical forms, starting with the evaluation.

The objective is to compute the probability (or likelihood) of the observed sequence O_t given a model. A dynamic programming technique is used to break down the probability of the sequence of observations into two probabilities:

The likelihood is computed by marginalizing over all the hidden states [7:6]{S_i}:

If we use the notation introduced in the previous chapter for alpha and beta variables, the probability for the observed sequence O_t given a model can be expressed as:

The product of the probabilities α and β can potentially underflow. Therefore, it is recommended to use the log of the probabilities instead of the probabilities.

class Pass(_lambda: HMMLambda, _obs: Array[Int]) extends HMMModel(_lambda, _obs) {  //1
   var alphaBeta: Matrix[Double] = _
   val ct = Array.fill(lambda.getT)(0.0) //2

   def normalize(t: Int): Unit = {
     ct.update(t, foldLeft(lambda.getN, (s, n) => s + alphaBeta(t, n))) //3
     alphaBeta /= (t, ct(t))
   }
}

class Alpha(lambda: HMMLambda, obs: Array[Int]) extends Pass(lambda, obs)

Import HMMConfig._
val alpha = { 
  alphaBeta = lambda.initAlpha(obs) //4
  normalize(0)  //5
  sumUp //6
}

def sumUp: Double = { //[M2]
  foreach(lambda.getT, t => {
    updateAlpha(t) //7
    normalize(t) //8
  })
  foldLeft(lambda.getN, (s, k) => s + alphaBeta(lambda.dim_1, k))
}

def updateAlpha(t: Int): Unit = 
  HMMConfig.foreach(lambda.getN, i => 
    alphaBeta += (t,i,lambda.alpha(alphaBeta(t-1,i),i,obs(t))) 
   )
}

def logProb: Double = foldLeft(lambda.getT, (s, t)
                    => s + Math.log(ct(t)), Math.log(alpha))//9

class Beta(lambdaB: HMMLambda, _obs: Array[Int]) extends Pass(lambdaB, _obs)

val complete = { //4
   alphaBeta = Matrix[Double](lambda.getT, lambda.getN)
   alphaBeta += (lambda.dim_1, 1.0) //1
   normalize(lambda.dim_1)  //2
   sumUp; true
}

def sumUp: Unit = //3
  (lambda.getT-2 to 0 by -1).foreach( t =>{
    updateBeta(t)
    normalize(t) 
})

def updateBeta(t: Int): Unit =
  foreach(lambda.config.getN, i => { 
    alphaBeta += (t, i, lambda.beta(alphaBeta(t+1, i), i, obs(t+1)))
})

The objective of this canonical form is to extract the model given a set of observations and a sequence of states. It is similar to the training of a classifier. The simple dependency of a current state on the previous state enables an implementation using an iterative procedure, known as the Baum-Welch estimator or expectation-maximization (EM).

Baum-Welch estimator (EM)

At its core, the algorithm has three steps and an iterative method, similar to the evaluation canonical form:

1. Compute the probability π (the gamma value at t=0) [M9].
2. Compute and normalize the state's transition probabilities matrix A [M10].
3. Compute and normalize the matrix of emission probabilities B [M11].
4. Repeat steps 2 and 3 until the change of likelihood is insignificant.

The algorithm uses the digamma and summation gamma variables defined in the HMMConfig class.

Note

The Baum-Welch algorithm

• M8: Joint probability of the state q_i at t and q_j at t+1:
  
  
• M9: The initial probabilities vector:
  
• M10: Update of the transition probabilities matrix:
  
• M11: Update of the emission probabilities matrix :
  

The Baum-Welch algorithm requires the following three inputs:

• The model, _lambda, initialized with random values uniformly distributed
• The current state of the training, state
• The labeled observed data, _obsIdx

The implementation of the Baum-Welch algorithm illustrates the elegance and conciseness of the Scala programming language. The constructor requires a fourth parameter to describe the minimum rate of change of the estimate of the likelihood between iterative calls, as shown in the following code snippet:

class BaumWelchEM config: HMMConfig, obs: Array[Int], numIters: Int,eps: Double) extends HMMModel(HMMLambda(config), obs) {
  val state = HMMState(lambda, numIters)
}

The model has to be initialized with the configuration parameters (number of observations, number of states, and number of symbols). The matrices A and B and the initial state probabilities pi are initialized with a uniform random generator [0, 1], Matrix.fillRandom, as shown here:

object HMMLambda {
  def apply(config: HMMConfig): HMMLambda = {
    val A = Matrix[Double](config._N)
    A.fillRandom(0.0)
    val B = Matrix[Double](config._N, config._M)
    B.fillRandom(0.0)
    val pi = Array.fill(config._N)(Random.nextDouble)
    new HMMLambda(A, B, pi, config._T)
   }

The maximum likelihood, maxLikelihood, is computed as part of the constructor to ensure a consistent state:

var likelihood = frwrdBckwrdLattice
Range(0, state.maxIters) find( _ => {
   lambda.estimate(state, obs)   //1
   val _likelihood = frwrdBckwrdLattice  //2
   val diff = likelihood - _likelihood  //3
   likelihood = _likelihood
   diff < eps  //4
}) match {
   case Some(index) => maxLikelihood
…

The computation of the likelihood requires the estimation of the transition matrix A and emission matrix B (line 1). The training process iterates by traversing the lattice forward and backward until the likelihood reaches a local or global maximum. The model is updated using the estimate method (line 1). The method computes the likelihood of the sequence of states (line 2) and then compares it with the likelihood computed in the previous iteration (line 3). The method exits if the difference between two consecutive likelihood values meets the convergence criteria eps (line 4).

The estimate method of the HMMLambda class updates the model (A, B, and pi):

def estimate(state: HMMState, obsIdx: Array[Int]): Unit = {
  pi = Array.tabulate(config._N)(i => state.Gamma(0, i) )
  HMMConfig.foreach(config._N, i => {
     
  var denominator = state.Gamma.fold(dim_1, i)
  HMMConfig.foreach(config._N, k => 
     A += (i, k, state.DiGamma.fold(dim_1, i, k)/denominator)
  )
  denominator = state.Gamma.fold(config._T, i)
  HMMConfig.foreach(config._N, k => B += (i, k, state.Gamma.fold(config._T, i, k, obsIdx)/denominator))
})

The core of the Baum-Welch expectation maximization is the iterative forward and backward update of the lattice of states and observations between time t and t+1. The lattice-based iterative computation is illustrated in the following diagram:

Visualization of HMM graph lattice for the Baum-Welch algorithm

The iteration across the lattice is implemented by the frwrdBckwrdLattice method (line 2). The lattice is traversed ahead using the Alpha instance class (line 1), and backward using the Beta instance class (line 2):

def frwrdBckwrdLattice: Double  = {
   val _alpha = Alpha(lambda, obs).alpha //1
   val _beta = Beta(lambda, obs) //2
   val a = _alpha.alphaBeta
   val b = _beta.alphaBeta
   Gamma.update(a, b)  //3
   DiGamma.update(a, b, A, B, obs) //4
   _alpha.alpha
}

The method returns the alpha coefficient and computes the new values for the Gamma (line 3) vector and DiGamma (line 4) matrix. These HMMState methods are omitted for the sake of clarity.

This last canonical form consists of extracting the most likely sequence of states {q_t} given a set of observations O_t and a model. Solving this problem requires, once again, a recursive algorithm.

The Viterbi algorithm

The extraction of the best state sequence (the sequence of state that has the highest probability) is very time consuming. An alternative consists of applying a dynamic programming technique to find the best sequence {q_t} through iteration. The algorithm is known as the Viterbi algorithm. Given a sequence of states {q_t} and sequence of observations {o_j}, the probability δ_t(i) for any sequence to have the highest probability path for the first T observations is defined for the state S_t [7:7].

Note

The Viterbi algorithm

M12: Definition of delta function:

M13: Initialization of delta:

M14: Recursive computation of delta:

M15: Computation of the optimum state sequence Q:

The constructor of the Viterbi algorithm, ViterbiPath, is similar to the algorithms of the first two canonical forms, and therefore, inherits HMMInference. The purpose of the Viterbi algorithm is to compute the optimum sequence given a set of observations and a model by maximizing the delta, maxDelta:

class ViterbiPath(_lambda: HMMLambda, _state: HMMState, _obs: Array[Int]) extends HMMInference(_lambda, _state, _obs) {
  val maxDelta = recurse(lambda.getT, 0)
  …
}

The recursive method that implements [M14] and [M15] steps is invoked by the constructor:

def recurse(t: Int, j: Int): Double = {
  var maxDelta = initial((t, j)) //1
  if( maxDelta == -1.0) {
    if(t != obs.size) {
        maxDelta = maxBy(lambda.getN, //2 [M14]
           s => recurse(t-1, s)* lambda.A(s, j)* lambda.B(j, obs(t)) 
         )
       val idx =maxBy(lambda.getT, i =>recurse(t-1 ,i)*lambda.A(i,j))  //3 [M14]

       state.psi += (t, j, idx) //4
       state.delta += (t, j, maxDelta) //5
     }
     else {  //6
       maxDelta = 0.0  
       val index =maxBy(lambda.getN, i => {
          val delta = recurse(t-1 ,i)
          if( delta > maxDelta) maxDelta = delta
          delta
       })
       state.QStar.update(t, index) //7
     }
   }
   maxDelta
}

Once initialized (line 1), the maximum value of delta, maxDelta, is computed recursively by applying the formula [M14] at each state, s, using Scala's maxBy method (line 2). Next, the index of the column of the transition matrix A corresponding to the maximum of delta is computed (line 3). The last step is to update the matrix psi (line 4) (with respect to delta (line 5)). Once the step t reaches the maximum number of observation labels (line 6), the optimum sequence of states q* is computed [M15] (line 7). Ancillary methods are omitted.

This implementation of the decoding form of the hidden Markov model completes the description of the hidden Markov model and its implementation in Scala. Now, let's put this knowledge into practice.

The main class HMM implements the three canonical forms. A view bound to an array of integers is used to parameterize the HMM class. We assume that a time series of continuous or pseudocontinuous values is converted (or categorized) into discrete symbol values.

The @specialized annotation ensures that the byte code is generated for the Array[Int] primitive without executing the conversion implicitly declared by the bound view. The HMM can be potentially used as part of a computation workflow, and therefore, has to implement the pipe operator (PipeOperator).

There are two different constructors for the HMM class. The first constructor uses the model as input (evaluation (CF1) and decoding (CF3)):

class HMM[@specialized T <% Array[Int]](lambda: HMMLambda, form: HMMForm, maxIters: Int) (implicit f: DblVector => T) extends PipeOperator[T, HMMPredictor] {
  val state = HMMState(lambda, maxIters)
….
}

The HMMForm enumerator is used to specify the canonical form of the HMM solution:

object HMMForm extends Enumeration {
type HMMForm = Value
val EVALUATION,DECODING = Value
}

The conversion of DblVector to a type T is required only if the evaluation and decoding canonical form uses actual observation values as argument. The f function is then used to discretize the double values into a sequence of index of the observations.

The HMMPredictor type consists of a tuple log probability (or likelihood) of observations and index of sequence of observations:

type HMMPredictor = (Double, Array[Int])

The HMM has three canonical forms instead of the two forms of most classifiers.

The second canonical form, training, is implemented by defining a second constructor for the HMM class, as follows:

object HMM {
  def apply[T <% Array[Int]](config: HMMConfig, obs: Array[Int], form: HMMForm, maxIters: Int, eps: Double)
                     (implicit f: DblVector => T): HMM[T] = {
    val baumWelchEM = new BaumWelchEM(config, obs, maxIters, eps)
    new HMM[T](baumWelchEM.lambda, form, maxIters)
  }
}

The decode (with respect to evaluate) method implements the third (with respect to the first) canonical form of HMM. Both methods take a sequence of indices for observations as an argument.

  def decode(obsIdx: Array[Int]): HMMPredictor = (ViterbiPath(lambda, state, obsIdx).maxDelta, state.QStar())
  def evaluate(obsIdx: Array[Int]): HMMPredictor = (-Alpha(lambda, obsIdx).logProb, obsIdx)
}

The data transformation |> encapsulates the evaluation and decoding forms in order to preserve its meaning. The observation, obs, is automatically converted into a sequence of indices to each observation (line 1) by the DblVector => T discretization function, which is an implicit parameter of the HMM class.

def |> : PartialFunction[DblVector, HMMPredictor] = {
  case obs: DblVector if(obs != null && obs.size > 2) => {
    form match {
      case EVALUATION => evaluate(obs)  //1
      case DECODING => decode(obs)  //1
    }
… 

Our test case is to train an HMM to predict the sentiment of investors as measured by the weekly sentiment survey of the members of the American Association of Individual Investors (AAII) [7:8]. The goal is to compute the transition probabilities matrix A, the emission probabilities matrix B, and the steady state probability distribution π, given the observations and hidden states (training canonical form).

We assume that the change in investor sentiments is independent of time, as required by the hidden Markov model.

The AAII sentiment survey grades the bullishness on the market in terms of percentage:

The weekly AAII market sentiment (reproduced by courtesy from AAII)

The sentiment of investors is known as a contrarian indicator of the future direction of the stock market. Refer to the Terminology section in Appendix A, Basic Concepts.

Let's select the ratio of percentage of investors that are bullish over the percentage of investors that are bearish. The ratio is then normalized. The following table lists this:

The sequence of non-normalized observations (ratio of bullish sentiment over bearish sentiment) is defined in a CSV file as follows:

final val OBS_PATH = "resources/data/chap7/obs.csv"

final val NUM_SYMBOLS = 6
final val NUM_STATES = 5
final val EPS = 1e-3
final val MAX_ITERS = 250
  

val srcObs =  Source.fromFile(OBS_PATH)
val obs = srcObs.getLines.map(_.toDouble)).toSeq //1
val config = new HMMConfig(obs.size, NUM_STATES, NUM_SYMBOLS)
val min = obs.min
val delta = obs.max - min
val obsSeq = obs.map( x => (x - min)/delta) //2
                .map(x =>(x*NUM_SYMBOLS).floor.toInt) //3
HMM[Array[Int]](config,obsSeq,EVALUATION,MAX_ITERS,EPS) match {
  case Some( hmm) => //4 
     Display.show(s"Lambda: ${hmm.getModel.toString}", logger)
   …
}

The sequence of observations is loaded from the CSV file (line 1) before being normalized (line 2). The discretization converts the normalized bullish sentiment/bearish sentiment ratio in six levels (integers) [0,-5] (line 3). The instantiation of the HMM class for the ratio levels (Array[Int]) generates the model (A, B, and pi) (line 4).

The following is a state-transition matrix:

The emission matrix is as follows:

The evaluation form of the hidden Markov model is very suitable for filtering data for discrete states. Contrary to time series filters such as the Kalman filter introduced in the The Kalman filter section in Chapter 3, Data Preprocessing, HMM requires data to be somewhat stationary in order to create a reliable model. However, the hidden Markov model overcomes some of the limitations of analytical time series analysis. Filters and smoothing techniques assume that the noise (frequency mean, variance, and covariance) is known and usually follows a Gaussian distribution. The hidden Markov model does not have such a restriction. Moreover, moving averaging techniques, discrete Fourier transforms, and generic Kalman filters require the states to be continuous with linear dependencies, although the extended Kalman filter can approximate nonlinear states.