7.3 Econometric Approach to VaR Calculation
A general approach to VaR calculation is to use the time series econometric models of Chapters 2–4. For a log return series, the time series models of Chapter 2 can be used to model the mean equation, and the conditional heteroscedastic models of Chapter 3 or 4 are used to handle the volatility. For simplicity, we use GARCH models in our discussion and refer to the approach as an econometric approach to VaR calculation. Other volatility models, including the nonlinear ones in Chapter 4, can also be used.
Consider the log return rt of an asset. A general time series model for rt can be written as
Equations (7.5) and (7.6) are the mean and volatility equations for rt. These two equations can be used to obtain 1-step-ahead forecasts of the conditional mean and conditional variance of rt assuming that the parameters are known. Specifically, we have
If one further assumes that ϵt is Gaussian, then the conditional distribution of rt+1 given the information available at time t is 
. Quantiles of this conditional distribution can easily be obtained for VaR calculation. For example, the 95% quantile is 
. If one assumes that ϵt is a standardized Student-t distribution with v degrees of freedom, then the quantile is 
, where 
is the (1 − p)th quantile of a standardized Student-t distribution with v degrees of freedom.
The relationship between quantiles of a Student-t distribution with v degrees of freedom, denoted by tv, and those of its standardized distribution, denoted by 
, is
where v > 2. That is, if q is the pth quantile of a Student-t distribution with v degrees of freedom, then 
is the pth quantile of a standardized Student-t distribution with v degrees of freedom. Therefore, if ϵt of the GARCH model in Eq. (7.6) is a standardized Student-t distribution with v degrees of freedom and the upper tail probability is p, then the (1 − p)th quantile used to calculate the 1-period horizon VaR at time index t is
where tv(1 − p) is the (1 − p)th quantile of a Student-t distribution with v degrees of freedom.
Example 7.3
Consider again the daily IBM log returns of Example 7.2. We use two volatility models to calculate VaR of 1-day horizon at t = 9190 for a long position of $10 million. These econometric models are reasonable based on the modeling techniques of Chapters 2 and 3.
Because the position is long, we use 
, where 
is the usual log return of IBM stock shown in Figure 7.1.
Assume that ϵt is standard normal. The fitted model is
From the data, we have r9189 = 0.00201, r9190 = 0.0128, and 
. Consequently, the prior AR(2)–GARCH(1,1) model produces 1-step-ahead forecasts as
The 95% quantile is then
The VaR for a long position of $10 million with probability 0.05 is VaR = $10, 000, 000 × 0.02877 = $287, 700. The result shows that, with probability 95%, the potential loss of holding that position next day is $287, 200 or less assuming that the AR(2)–GARCH(1,1) model holds. If the tail probability is 0.01, then the 99% quantile is
The VaR for the position becomes $409, 738.
Assume that ϵt is a standardized Student-t distribution with 5 degrees of freedom. The fitted model is
From the data, we have r9189 = 0.00201, r9190 = 0.0128, and 
. Consequently, the prior Student-t AR(2)–GARCH(1,1) model produces 1-step-ahead forecasts
The 95% quantile of a Student-t distribution with 5 degrees of freedom is 2.015 and that of its standardized distribution is 
. Therefore, the 95% quantile of the conditional distribution of r9191 given F9190 is
The VaR for a long position of $10 million is
which is essentially the same as that obtained under the normality assumption. The 99% quantile of the conditional distribution is
The corresponding VaR is $475, 943. Comparing with that of Case 1, we see the heavy-tail effect of using a Student-t distribution with 5 degrees of freedom; it increases the VaR when the tail probability becomes smaller. In R and S-Plus, the quantile of a Student-t distribution with m degrees of freedom can be obtained by the command qt(p,m), for example, xp = qt(0.99,5.23) for the 99th percentile of a Student-t distribution with 5.23 degrees of freedom.
7.3.1 Multiple Periods
Suppose that at time h we want to compute the k-horizon VaR of an asset whose log return is rt. The variable of interest is the k-period log return at the forecast origin h (i.e., rh[k] = rh+1 + ⋯ + rh+k). If the return rt follows the time series model in Eqs. (7.5) and (7.6), then the conditional mean and variance of rh[k] given the information set Fh can be obtained by the forecasting methods discussed in Chapters 2 and 3.
7.3.1.1 Expected Return and Forecast Error
The conditional mean E(rh[k]|Fh) can be obtained by the forecasting method of ARMA models in Chapter 2. Specifically, we have
where rh(ℓ) is the ℓ-step-ahead forecast of the return at the forecast origin h. These forecasts can be computed recursively as discussed in Section 2.6.4. Using the MA representation
of the ARMA model in Eq. (7.5), we can write the ℓ-step-ahead forecast error at the forecast origin h as
see Eq. (2.33) and the associated forecast error. The forecast error of the expected k-period return 
is the sum of 1-step to k-step forecast errors of rt at the forecast origin h and can be written as
7.7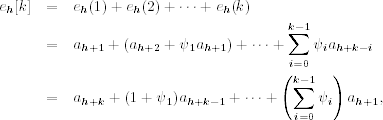 
where ψ0 = 1.
7.3.1.2 Expected Volatility
The volatility forecast of the k-period return at the forecast origin h is the conditional variance of eh[k] given Fh. Using the independent assumption of ϵt+i for i = 1, … , k, where at+i = σt+iϵt+i, we have
where Vh(z) denotes the conditional variance of z given Fh and 
is the ℓ-step-ahead volatility forecast at the forecast origin h. If the volatility model is the GARCH model in Eq. (7.6), then these volatility forecasts can be obtained recursively by the methods discussed in Chapter 3.
As an illustration, consider the special time series model
Then we have ψi = 0 for all i > 0. The point forecast of the k-period return at the forecast origin h is 
and the associated forecast error is
Consequently, the volatility forecast for the k-period return at the forecast origin h is
Using the forecasting method of GARCH(1,1) models in Section 3.5, we have
Using Eq. (7.9), we obtain that for the case of ψi = 0 for i > 0,
7.10 
where ϕ = α1 + β1 < 1. If ψi ≠ 0 for some i > 0, then one should use the general formula of Var(eh[k]|Fh) in Eq. (7.8). If ϵt is Gaussian, then the conditional distribution of rh[k] given Fh is normal with mean kμ and variance Var(eh[k]|Fh). The quantiles needed in VaR calculations are readily available. If the conditional distribution of at is not Gaussian (e.g., a Student-t or generalized error distribution), simulation can be used to obtain the multiperiod VaR.
Example 7.3 (Continued)
Consider the Gaussian AR(2)–GARCH(1,1) model of Example 7.3 for the daily log returns of IBM stock. Suppose that we are interested in the VaR of a 15-day horizon starting at the forecast origin 9190 (i.e., December 31, 1998). We can use the fitted model to compute the conditional mean and variance for the 15-day log return via 
given F9190. The conditional mean is − 0.00998 and the conditional variance is 0.0047948, which is obtained by the recursion in Eq. (7.9). The 95% quantile of the conditional distribution is then 
. Consequently, the 5% 15-day horizon VaR for a long position of $10 million is VaR = $10, 000, 000 × 0.1039191 = $1, 039, 191. This amount is smaller than 
. This example further demonstrates that the square root of time rule used by RiskMetrics holds only for the special white noise IGARCH(1,1) model used. When the conditional mean is not zero, proper steps must be taken to compute the k-horizon VaR.
7.3.2 Expected Shortfall under Conditional Normality
We can use the result of Section 7.2.4 to calculate the ES when the conditional distribution of the log return is 
. The result is
where q = 1 − p and xq is the qth quantile of the standard normal distribution. For instance, if p = 0.01, then ES0.99 = μt + 2.6652σt.